News :: Erreur :: Visiteurs :: ClearType :: Imprimer ::

ÉLECTROSTATIQUE | MAGNÉTOSTATIQUE | ÉLECTRODYNAMIQUE | ÉLECTROCINÉTIQUE
OPTIQUE GÉOMÉTRIQUE | OPTIQUE ONDULATOIRE

Dernière mise à jour de ce chapitre: 2015-09-06 16:34:27 | {oUUID 1.776}
Version: 3.1 Révision 9 | Rédacteur: Vincent ISOZ  | Avancement: ~40%
vues depuis le 2012-01-01: 7'809

LISTE DES SUJETS TRAITÉS SUR CETTE PAGE

Le développement de l'électrodynamique a permis à une grande partie de l'humanité de modifier considérablement sa qualité de vie. Nous savons à peu près tous aujourd'hui ce que nous lui devons: lumière, frigo, radio, télévision, ordinateurs, voitures, trams, trains, avions, robots, et d'autres choses merveilleuses et parfois moins aussi...

Avant de commencer à étudier l'électrocinétique (les ingénieurs parlent "d'électronique" ou "d'électrotechnique") nous allons définir les deux lois (le terme est mal choisi puisque la première est démontrée dans le chapitre d'Électrostatique et la seconde dans le chapitre d'Électrodynamique mais bon... conformons-nous à la tradition...) fondamentales de l'étude de l'électrocinétique et la terminologie de base des circuits ou installations électriques (les cas pratiques étant étudiés dans le chapitre de Génie Électrique). Même si certains éléments au début ne seront peut-être pas compris de suite par le lecteur, ceux-ci deviendront triviaux au fur et à mesure de l'avancement de sa lecture.

Définitions:

D1. Un circuit électrique est constitué d'un ensemble de dispositifs appelés "dipôles", reliés entre eux par un fil conducteur.

D2. Un "noeud" d'un circuit est une interconnexion où arrivent 3 fils ou plus.

D3. Une "branche" est un tronçon de circuit situé entre deux noeuds.

D4. Enfin, une "maille" est un ensemble de branches formant une boucle fermée.

Le dipôle est caractérisé par la réponse du courant I à une différence de potentiel U entre ses bornes: c'est à dire par la courbe caractéristique:

  (38.1)

Nous verrons que dans tout conducteur, la présence d'une résistivité (voir plus loin) entraîne une chute de tension et, en toute rigueur, il en va de même pour les fils. Mais ceux-ci étant mis en série avec d'autres dipôles, nous négligeons en général dans les petits circuits la résistance des fils devant celle des dipôles présents. Donc, les fils situés entre deux dipôles d'un circuit seront supposés équipotentiels (le potentiel est le même sur les deux bornes).

LOIS DE KIRCHHOFF

Les lois de Kirchhoff en électrocinétique (à ne pas confondre avec celles de la thermodynamique et de l'optique) expriment les propriétés physiques de la charge et du champ électrique et sont donc au nombre de deux (une loi pour chaque).

Elles vont nous permettre sans faire appel à l'artillerie mathématique implicitement cachée derrière d'obtenir simplement des résultats forts pertinents.

LOI DES MAILLES

La loi des mailles (implicitement il s'agit simplement de la conservation de l'énergie) exprime le fait que lorsqu'une charge parcourt un circuit fermé (chemin fermé), l'énergie qu'elle perd en traversant une partie du circuit est égale à l'énergie qu'elle gagne dans l'autre partie. Ainsi, la somme algébrique des potentiels le long d'une maille est nulle telle que:

  (38.2)

Pour cela, il faut choisir arbitrairement un sens de parcours de la maille et convenir que les tensions dont la flèche pointe dans le sens du parcours sont comptées comme positives et les autres comme négatives.

LOI DES NOEUDS

La loi des noeuds (implicitement il s'agit simplement de la conservation du courant) exprime la conservation de la charge qui signifie que la somme des courants sortant d'un noeud (un noeud peut être vu comme un séparateur de lignes de champ - in extenso des volumes rattachés par une même surface) est égale à la somme des courants entrants. Autrement dit, la somme algébrique des courants est nulle en tout noeud d'un circuit tel que:

  (38.3)

Pour cela, il faut choisir un signe pour les courants entrants et le signe contraire pour les courants sortants (comme nous le faisons en thermodynamique avec la masse).

MODÈLE DE DRUDE

Le modèle de Drude de la conduction électrique va nous permettre d'introduire les concepts élémentaires de l'électrocinétique. Dans un premier temps, nous allons définir dans ce qui va suivre les concepts de courant, de densité de courant et ensuite de résistance.

Un conducteur électrique (nous ne parlons pas de semi-conducteurs ou supraconducteurs à ce niveau du discours) peut être vu de manière très simplifiée comme un tuyau de section  contenant un gaz d'électrons formé de n charges élémentaires q par unité de volume.

En l'absence de champ électrique, chaque électron possède une vitesse moyenne vectorielle nulle car il reste au voisinage de l'atome. Sous l'action d'un champ électrique homogène et constant (cas du courant continu donc!), certains électrons sont déplacés dans une direction privilégiée, jusqu'à ce qu'ils entrent en collision avec un autre atome (aspect classique) où ils reprennent une vitesse moyenne de dérive nulle et ainsi de suite.

C'est le modèle le plus ancien et le plus élémentaire du courant électrique. Les bases en furent jetées par Drude en 1902, peu après la découverte de l'électron par Thomson (1897). D'où le nom de "modèle de Drude".

Insuffisant pour concevoir et a fortiori développer les composants qui forment depuis la fin du 20ème siècle l'essentiel des éléments actifs utilisés en électronique, le modèle des boules de billard présente néanmoins des intérêts considérables:

- C'est un auxiliaire utile pour donner à notre esprit une image de phénomènes dont nous n'avons en fait aucune perception directe, puisqu'ils se déroulent dans l'infiniment petit.

- Les résultats, pour l'ingénieur, de théories plus exactes, comme la théorie des bandes d'énergie en particulier, se laissent formuler au moyen des mêmes concepts que ceux qui apparaissant dans le modèle Boules de billard. Citons parmi ceux-ci le nombre volumique et la mobilité des électrons.

- Tout primitif qu'il soit, ce modèle conduit à une interprétation phénoménologique intéressante des lois fondamentales telles que la loi d'Ohm ou la loi de Joule. Il lie les phénomènes microscopiques à certaines grandeurs observables.

Son nom l'indique, ce modèle assimile les électrons à de minuscules boules de billard. Ces particules sont donc des objets classiques, simplement régis par la loi de Newton et les lois de Maxwell. Cette conception corpusculaire de l'électron n'est d'ailleurs pas totalement opposée aux résultats de la mécanique quantique, dans laquelle un paquet d'ondes, peut toujours être interprété comme une particule, avec sa masse et sa vitesse (voir le théorème d'Ehrenfest dans le chapitre de Physique Quantique Ondulatoire).

Dans un millimètre cube de cuivre, nous admettrons que le nombre d'électrons est tellement élevé qu'il n'est donc alors pas question de les traiter individuellement, ce qui serait d'ailleurs sans intérêt. C'est le comportement moyen des électrons qu'il convient d'étudier. Deux types d'interactions conditionnent ce comportement, ce sont:

- l'interaction des électrons avec la matière dans laquelle ils évoluent, et dont ils font partie;

- l'interaction des électrons avec les champs électromagnétiques appliqués de l'extérieur.

La distance  parcourue par un électron est appelée "libre parcours moyen de l'électron de conduction" et si  est l'intervalle de temps entre deux collisions successives alors nous avons trivialement:

  (38.4)

Le temps de collision est une variable aléatoire. Tous paramètres physiques restants constants, cette variable aléatoire est stationnaire, sa valeur moyenne porte le nom de "temps de collision moyen".

Nous supposons que:

  (38.5)

la vitesse moyenne, est créée par l'accélération du champ électrique:

  (38.6)

Nous obtenons alors la " vitesse moyenne de dérive" ou "vitesse d'entraînement" des électrons (drift velocity) donnée par:

  (38.7)

Cette relation est nommée ainsi, car leur vitesse initiale est due à l'agitation thermique entretenue de l'environnement extérieur et correspond à la vitesse thermique dont nous avons déterminé l'expression lors de notre étude de la distribution de Maxwell-Boltzmann dans le chapitre de Mécanique Statistique (nous en calculerons les valeurs un peu plus bas dans le présent texte).

Nous admettons donc, dans le cadre du modèle Boules de billard, que les électrons se comportent comme les atomes d'un gaz parfait. C'est une hypothèse grossière mais suffisante pour l'instant!

La vitesse moyenne est supposée identique pour tous les électrons libres lorsque le champ électrique appliqué est supposé uniforme, stationnaire, et dirigé selon un seul axe. Elle permet de définir "l'intensité" I du courant électrique dans le conducteur.

Définition: Le "courant" ou "intensité"  I mesure la charge qui traverse la section droite  S d'un conducteur par unité de temps dt et est donc donné selon ce qui a été montré juste avant par:

  (38.8)

Une tranche de conducteur, de volume  contient donc la charge:

  (38.9)

Elle traverse la section S en un temps dt, tel que:

  (38.10)

Le courant s'écrit alors:

  (38.11)

Si I est vu comme le flux d'une "densité de courant" J à travers la surface S, nous avons alors:

  (38.12)

la densité de courant étant supposée constante sur chaque point de la surface.

Nous avons donc:

  (38.13)

et après simplification:

  (38.14)

qui est donc l'expression de la "densité de courant" dans le conducteur.

Comme nous connaissons l'expression de la vitesse, nous pouvons écrire:

  (38.15)

En nous définissons la "conductivité" par: 

  (38.16)

où cette fois n désigne non pas le nombre d'électrons, mais le nombre volumique d'électrons! Par définition, la "résistance" est l'inverse de la conductivité.

Nous remarquons que la conductivité contient le produit du nombre volumique des électrons par leur mobilité. Il faut par conséquent que l'une au moins de ces grandeurs ait une valeur élevée pour qu'un matériau présente une haute conductivité.

La mobilité est plus grande dans les semi-conducteurs que dans les métaux. Cette caractéristique est cependant complètement masquée par le rapport des nombres volumiques des électrons: n est 1'000'000 à 100'000'000 fois plus faible dans les semi-conducteurs que dans les métaux, ce qui explique la conductivité supérieure de ces derniers.

Selon la relation:

  (38.17)

démontrée juste plus haut, la conductivité dépendrait du champ électrique, par l'intermédiaire du temps de collision. En effet, plus le champ électrique croît, plus la vitesse des électrons augmente. La distance entre les points de chocs possibles restant la même, le temps de collision, et par conséquent la conductivité, devraient diminuer (et donc la résistance augmenter!).

Or, l'indépendance de la conductivité (et respectivement de la résistance) avec le champ électrique est un fait expérimental établi avec précision dans tous les conducteurs habituels dans des conditions normales d'utilisations civiles.

L'origine de cette contradiction réside dans la différence considérable des ordres de grandeur de la vitesse thermique donnée par la distribution de Maxwell-Boltzmann (cf. chapitre de Mécanique Statistique):

  (38.18)

et la vitesse moyenne de dérive vue plus haut:

  (38.19)

avec le temps de libre parcours moyen qui sera obtenu à l'aide de l'expression:

  (38.20)

Nous avons vu dans le chapitre de Mécanique Statistique que pour un électron à température ambiante:

  (38.21)

Et calculons la vitesse de dérive pour le cuivre avec dans ce métal particulier les valeurs suivantes:

 et   (38.22)

Ce qui nous permet d'obtenir la valeur:

  (38.23)

et donc:

  (38.24)

En prenant , ce qui est à considérer comme une valeur élevée puisque ce champ produit une densité de courant de:

  (38.25)

nous avons finalement:

  (38.26)

Par conséquent, même dans un fort champ électrique industriel, la vitesse de dérive est négligeable par rapport à la vitesse thermique.

Comme la vitesse thermique ne dépend que très peu du champ électrique, il s'avère qu'en pratique la vitesse des électrons est indépendante du champ électrique. En d'autres termes, l'établissement d'un courant, même intense, n'a qu'une incidence absolument négligeable sur la vitesse des électrons!

Cependant, un point important à constater est le calcul du libre parcours moyen des électrons dans le modèle classique de Drude. Nous avons effectivement:

  (38.27)

qui est donc très supérieur, d'au moins un ordre de grandeur (facteur 10), aux distances interatomiques. Il en résulte que les collisions successives sur les atomes du réseau ne sont pas responsables de la loi d'Ohm (que nous allons voir maintenant) contrairement à une des hypothèses de départ du modèle de Drude mais que ce sont les impuretés et les défauts du matériau qui en sont responsables! Nous verrons aussi un peu plus loin qu'avec le modèle théorique des bandes d'énergie le libre parcours moyen est au fait nettement plus grand encore!

Attention!!! Cette relation peut faire penser que puisque le libre parcours moyen est proportionnel à la vitesse thermique et donc proportionnel à la racine carrée de la température, alors la résistance diminue avec la température. Mais en fait il n'en est rien! Le modèle de Drude est trop simpliste car en réalité c'est l'inverse qui a lieu pour les conducteurs (la résistance augmente avec la température parce que l'intervalle de temps entre deux collisions diminue plus vite que la vitesse augmente). Et puis il y a aussi le problème inverse... à température presque nulle le libre parcours moyen serait presque nul or les supraconducteurs nous montrent bien qu'il n'en est rien! Bref, sans relation explicite en fonction de la température nous sommes dans l'obscurité la plus totale!

La seule chose que nous savons faire c'est admettre qu'à un facteur constant près (positif ou négatif), une variation de la température implique une variation relative de la résistance selon:

  (38.28)

soit:

  (38.29)

d'où la relation connue dans les petites classes:

  (38.30)

Enfin, précisons que la quatrième équation de Maxwell (cf. chapitre Électrodynamique) peut alors s'écrire au vu des résultats obtenus ci-dessus:

  (38.31)

qui fait alors apparaître explicitement le coefficient de conductivité.

LOI D'OHM

À partir de la relation démontrée précédemment:

  (38.32)

et en prenant la définition de la "conductivité" par: 

  (38.33)

Il vient finalement:

  (38.34)

qui est la "loi locale d'Ohm". Nous la retrouverons sous forme différentielle dans le chapitre de Mécanique Statistique et nous verrons qu'elle appartient au fait à la famille des lois de diffusion!

Si nous multiplions l'égalité sous forme scalaire à droite et à gauche par L nous obtenons:

  (38.35)

Donc nous avons:

 ou   (38.36)

Nous définissons l'inverse de la conductivité comme la "résistance électrique" définie par:

  (38.37)

Dès lors, nous pouvons écrire la loi d'Ohm sous sa forme la plus communément connue:

  (38.38)

où donc (attention!!!) le potentiel U représente la différence de potentiel sur la longueur de l'élément résistif (appelé également "dipôle résistif") comme nous le voyons dans les développements et non pas le potentiel total extérieur!

Puisque U est le potentiel de l'élément résistif, nous faisons alors souvent référence dans le domaine de l'électrotechnique à la "chute de potentiel" (effectivement, au-delà de l'élément résistif le potentiel n'est plus le même qu'au point qui précède ce même élément résistif).

Pour les câbles en cuivre typiques d'usage non industriel, il existe une table américaine très utile dans la pratique donnant avec une relativement bonne tolérance la résistivité en fonction du diamètre et le courant maximal admissible. Voici un échantillon de cette table:

où AWG signifie "American Wire Gauge" et correspond à une petite jauge qu'on peut acheter pour rapidement déterminer le diamètre d'un câble à l'aide de la table ci-dessus sans avoir un pied à coulisse:

Figure: 38.1 - Jauge AWG (source: Wikipédia)

RÉSISTANCES ÉQUIVALENTES

Nous pouvons maintenant nous intéresser sur toute la longueur d'une ligne de champ électrique parcourue colinéairement par un courant I supposé constant en tout point (c'est une approximation donc...) à la résistance totale si n éléments résistifs sont mis les uns à côtés des autres linéairement.

La réponse est relativement simple puisque si nous notons le potentiel à la première extrémité de l'élément résistif et l'autre extrémité, nous avons alors (le lecteur remarquera que l'usage de la loi des mailles dans la relation suivante se fait logiquement sans même avoir nécessairement connaissance de celle-ci):

  (38.39)

c'est-à-dire un résultat analogue à celui obtenu par une résistance unique dont la valeur est donnée approximativement par (si le courant est constant sur toute la ligne) la "résistance équivalente de résistances en série":

  (38.40)

qui est la somme arithmétique des résistances individuelles.

Considérons maintenant n résistances en parallèles toutes sous une tension U (de par la loi des mailles) et alimentées par un courant I. Le courant se sépare alors en n courants:

  (38.41)

Dans chacune des n branches. En vertu de la loi des noeuds, nous avons:

  (38.42)

c'est-à-dire que l'ensemble des résistances mises en parallèle est analogue à une "résistance équivalente de résistances en parallèle":

  (38.43)

donnée donc par la moyenne harmonique (cf. chapitre de Statistiques)!

Le fait de brancher des appareils en parallèle permet donc d'avoir toujours la même tension aux bornes de ceux-ci. C'est ainsi que sont disposées par ailleurs les prises électriques dans une installation domestique!

CAPACITÉS ÉQUIVALENTES

Nous pouvons de même, appliquer le même type de raisonnement aux capacités. Rappelons que nous avons défini dans le chapitre d'Électrostatique, la capacité comme étant donnée par:

  (38.44)

Considérons, au même titre que les résistances, n condensateurs de capacités mis en série les uns derrière les autres. Nous portons aux potentiels et les deux extrémités de la chaîne et nous apportons la charge Q sur l'ensemble du système. Le potentiel (tension) total aux bornes de la chaîne de condensateurs s'écrit alors simplement:

  (38.45)

et correspond donc à celle d'une capacité unique C de "capacité équivalente de capacités en série":

  (38.46)

où nous retrouvons une moyenne harmonique.

Considérons maintenant n condensateurs de capacités mis en parallèle avec le même potentiel U. La charge électrique de chacun d'entre eux est alors imposée (de par la loi des mailles) par la relation:

  (38.47)

La charge électrique totale est simplement:

  (38.48)

ce qui correspond à une "capacité équivalente de capacités en parallèle":

  (38.49)

qui est la somme arithmétique des capacités individuelles.

Enfin pour clore, rappelons que nous avons démontré dans le chapitre d'Électrostatique que:

  (38.50)

Dans le cas où une capacité est seule en série avec un générateur à courant alternatif sinusoïdal (cas assez typique dans le monde industriel du 19ème et 20ème siècle), alors nous aurons:

  (38.51)

Et donc il vient:

  (38.52)

Que nous écrirons en analogie avec la loi d'Ohm sous la forme:

  (38.53)

où:

  (38.54)

est appelée la "réactance capacitive". Nous remarquons que dans le cas continu où la pulsation est nulle, le réactance capacitive devient alors infinie et que nous retrouvons la situation connue où la capacité ne laisse pas passer de courant (du moins dans le cas idéal...).

FORCE ÉLECTROMOTRICE

Soit une portion AB d'un circuit, parcourue par un courant permanent I allant de A vers B. L'existence de ce courant implique que le potentiel en A est supérieur (différent) en valeur absolue à celui en B (en valeur absolue). Cette différence de potentiel se traduit par l'existence du champ électrostatique produisant une force de Coulomb:

  (38.55)

capable d'accélérer une charge q.

Ainsi, soit:

  (38.56)

la puissance nécessaire pour communiquer une vitesse v à une particule de charge q quelconque. Sachant que dans ce conducteur il y a porteurs de charge par unité de volume, la puissance totale P mise en jeu dans le brin AB parcouru par un courant I est:

  (38.57)

c'est-à-dire:

  (38.58)

où:

  (38.59)

Cette puissance est donc la "puissance électrique" disponible entre A et B, du simple fait qu'il y circule un courant I.

Si nous considérons dans ce circuit AB une partie résistive pour laquelle nous mesurons une différence de potentiel:

  (38.60)

alors la puissance disponible à l'intérieur de celui-ci est donnée par la "puissance joule":

  (38.61)

Ainsi, parmi cette puissance disponible, une certaine partie est dissipée sous forme de chaleur (effet Joule) dans un dipôle passif tel que la résistance. Évidemment c'est cette puissance que nous facture notre compagnie d'électricité et connaître l'énergie consommée, il suffit de multiplier la puissance de l'appareil que l'on utilise par la durée de fonctionnement.

Cependant, quelque chose cloche dans nos développements précédents si nous y regardons de plus près. Effectivement, si nous appliquons le raisonnement à un circuit fermé, c'est-à-dire si nous regardons la puissance totale fournie entre A et A par la force de Coulomb, nous obtenons (bien évidemment puisque le champ électrostatique coulombien est conservatif):

  (38.62)

c'est-à-dire une puissance nulle?! Eh oui! Cela signifie qu'il ne peut y avoir de courant en régime permanent dans une boucle fermée et lorsque qu'il y a un courant, alors cela implique que la force de Coulomb n'est pas responsable du mouvement global des porteurs de charge dans un conducteur!!

Dès lors, le courant dans un conducteur peut être compris avec l'analogie de la rivière circulant dans son lit. Pour qu'il y ait un écoulement, il faut que l'eau s'écoule d'une région plus élevée vers une région plus basse (d'un potentiel gravitationnel plus haut vers un autre plus bas). Ainsi, le mouvement de l'eau d'un point élevé vers un point plus bas est bien dû à la simple force de gravitation. Mais si nous voulons constituer un circuit fermé, alors il faut fournir de l'énergie (grâce à une pompe) pour amener l'eau à une plus grande hauteur et le cycle peut alors recommencer.

C'est exactement ce qui se passe dans un circuit électrique. Si nous voulons qu'un courant permanent circule, il faut qu'une autre force que la force électrostatique permette aux charges de fermer le chemin (c'est un raisonnement purement mathématique) ! C'est à ce titre que nous devons faire intervenir une source d'énergie "artificielle" externe tel que le "générateur électrique" qui est alors l'équivalent de la pompe hydraulique pour l'eau.

Le générateur doit alors nous imposer comme propriété physique que lorsque son circuit est ouvert (courant I étant alors nul) une "différence de potentiel" D.D.P. se maintienne entre ses bornes impliquant nécessairement la présence d'une autre force compensant l'attraction coulombienne du conducteur. Ainsi, la force totale s'exerçant sur une charge q s'écrit dès lors:

  (38.63)

avec étant le champ électrostatique et le "champ électromoteur". À l'équilibre et en l'absence de courant, nous devons avoir:

  (38.64)

Cela signifie que la D.D.P. aux bornes d'un générateur ouvert vaut alors:

  (38.65)

Nous appelons et notons:

  (38.66)

(un peu maladroitement) la "force électromotrice" FEM propre du générateur.

Puisque, à l'intérieur du générateur, nous avons:

  (38.67)

à circuit ouvert, cela signifie qu'un générateur est un conducteur non-équipotentiel (ou à "champ non conservatif").

À l'équilibre, mais en présence d'un courant I (générateur branché dans un circuit fermé), les porteurs de charge responsables de ce courant subissent une force supplémentaire, due aux collisions se produisant à l'intérieur du conducteur. Pour un générateur idéal, ces collisions sont négligeables et nous obtenons:

  (38.68)

En revanche, pour un générateur non idéal, de telles collisions se produisent et se traduisent par l'existence d'une résistance interne r (très faible pour les générateurs à l'état neuf!). Ainsi, la vraie force électromotrice est donnée par:

  (38.69)

La résistance interne du générateur introduit donc une chute de tension proportionnelle au courant fourni, ce qui fait qu'il délivre un potentiel inférieur à celui donné par sa FEM.

Cette dernière relation est parfois notée sous la forme suivante:

  (38.70)

et souvent avec l'écriture:

  (38.71)

ce que l'on mesure avec un voltmètre est cependant la FEM puisque les générateurs ont une résistance interne admise comme infinie et impliquent donc un courant I quasi nul.

Les générateurs diffèrent selon la source d'énergie utilisée et la méthode de conversion de celle-ci en énergie électrique (autrement dit, selon la nature de ). Nous pouvons ainsi produire de l'énergie électrique à partie d'une pile (énergie chimique), d'un générateur électrostatique (énergie mécanique), d'une dynamo (énergie mécanique), d'une pile solaire (énergie du rayonnement) ou d'un thermocouple (énergie chaleur).

Reprenons le calcul fait précédemment mais appliquons-le cette fois-ci à l'ensemble du circuit. Soit alors V le volume total occupé par le conducteur formant le circuit et la force s'exerçant sur les charges mobiles q et donc responsable de leur mouvement.

La puissance totale P qui doit être fournie en régime permanent est alors:

  (38.72)

où:

  (38.73)

est la FEM totale du circuit. L'intégrale portant sur l'ensemble du circuit, la FEM totale est donc la somme des FEM présentes le long du circuit (s'il y en a). Si celles-ci sont localisées dans des dipôles, l'expression devient:

  (38.74)

où les sont les valeurs algébriques des différentes FEM:

1. correspond à un "générateur" (production d'énergie électrique)

2. correspond à un "récepteur" (consommation d'énergie électrique)

Nous avons aussi pour la puissance électrique:

  (38.75)

et la puissance joule:

  (38.76)

Un moteur convertit de l'énergie électrique en énergie mécanique et correspond donc à un récepteur de FEM: nous disons également, qu'il possède une "force contre-électromotrice" ou FCEM.

LOI DE FARADAY

Maintenant que nous avons démontré la nécessité de la force électromotrice, nous allons pouvoir démontrer la provenance de la "loi de Faraday" ainsi que la "loi de Lenz" dont nous avions fait usage en électrodynamique pour démontrer la troisième équation de Maxwell. La détermination de la loi de Faraday va également nous permettre de définir le concept d'inductance et d'étudier ses propriétés.

Faisons la même démarche que Faraday et posons-nous la question suivante: Comment créé-t-on un courant?

Un courant est un déplacement de charges dans un matériau conducteur. Ces charges sont mises en mouvement grâce à une D.D.P. qui est maintenue par une FEM. Ainsi, une pile, en convertissant son énergie chimique pendant un instant dt fournit donc une puissance P modifiant l'énergie cinétique des dQ porteurs de charge produisant ainsi un courant I.

Soit la puissance nécessaire pour communiquer une vitesse à une particule de charge q. Sachant que dans un conducteur, il y a n porteurs de charge par unité de volume, la puissance totale P que doit fournir le générateur (idéal) est alors (voir plus haut):

  (38.77)

Nous posons donc que la FEM idéale d'un circuit est:

  (38.78)

Or, la force de Coulomb est incapable de produire une FEM comme nous l'avons démontré tout à l'heure. Pour créer un courant continu dans un circuit fermé, il faut donc un champ électromoteur dont la circulation le long du circuit ne soit pas nulle. L'expérience de Faraday montre donc que c'est l'existence du champ magnétique qui permet l'apparition du courant (!!!!). Cela signifie que la force de Lorentz doit être responsable de l'apparition d'une FEM, c'est-à-dire:

  (38.79)

Donc:

  (38.80)

Les propriétés du produit vectoriel (cf. chapitre de Calcul Vectoriel) nous donnant:

  (38.81)

nous pouvons écrire:

  (38.82)

Une petite remarque s'impose à ce niveau du discours. Si est bien le vecteur vitesse des charges q il ne peut être celui qui est colinéaire à car sinon nous aurions:

  (38.83)

et donc e serait nul et ceci n'est pas possible car contredirait tous les développements faits jusqu'à présent ! Au fait, est la vitesse de l'ensemble du circuit qui entraîne avec lui l'ensemble des charges à la même vitesse !

Ainsi, pendant un temps dt, le circuit se déplace d'une distance:

  (38.84)

vecteur qui est perpendiculaire à . Dès lors:

  (38.85)

est la surface (voir les propriétés du produit vectoriel dans le chapitre de Calcul Vectoriel) décrite par le déplacement de l'élément sur la distance tel que:

  (38.86)

Nous avons alors:

  (38.87)

Nous reconnaissons l'expression du flux (dit "flux coupé") à travers la surface élémentaire . Ce qui nous amène à écrire (il y a un petit peu d'intuition - bon sens - avec la manipulation des différentielles mais bon c'est aussi ça la physique...):

  (38.88)

Nous venons de démontrer la "loi de Faraday" dans le cas d'un circuit rigide plongé dans un champ magnétique varable. Nous avons vu apparaître naturellement l'expression du flux coupé. En fait, la seule chose qui compte, c'est l'existence d'un mouvement d'ensemble du tout ou d'une partie du circuit (revoir la démonstration pour s'en convaincre). Ainsi, l'expression de la FEM induite:

  (38.89)

reste valable pour un circuit déformé et/ou déplacé dans un champ magnétique statique. Cette démonstration s'est faite à partir de la force de Lorentz et est donc a priori indépendante du référentiel choisi!

LOI DE LENZ

L'énoncé de la loi de Lenz est le suivant: L'induction produit des effets qui s'opposent aux causes qui lui ont donné naissance.

Cette loi est, comme la règle du flux maximum, déjà contenue dans les équations et n'apporte rien de plus, hormis une intuition des phénomènes physiques. En l'occurrence, la loi de Lenz n'est que l'expression du signe "-" contenu dans la loi de Faraday.

Exemple:

Si nous approchons un circuit du pôle nord d'un aimant, le flux augmente et donc la FEM induite est négative. Le courant induit sera alors négatif et produira lui-même un champ magnétique induit opposé à celui de l'aimant. Deux conséquences:

1. L'augmentation du flux à travers le circuit est amoindrie.

2. Il apparaît une force de Laplace (cf. chapitre de Magnétostatique) négative, s'opposant à l'approche de l'aimant.

Ce signe "-" dans la loi de Faraday (la loi de Lenz) décrit le fait que dans des conditions normales, il n'y a pas d'emballement possible (exemple: courant ne faisant qu'augmenter).

C'est la raison pour laquelle la loi de Lorenz est souvent appelée "loi de Lenz-Faraday".

INDUCTANCE

Nous avons donc:

  (38.90)

Or la loi de Biot-Savart nous donne (cf. chapitre de Magnétostatique):

  (38.91)

Dès lors:

  (38.92)

que nous écrivons historiquement sous forme condensée de la manière suivante:

  (38.93)

où L est le "coefficient d'auto-induction" ou "auto-inductance" (ou "self"), exprimé en "Henry" [H]. Il ne dépend que des propriétés géométriques du circuit et est nécessairement positif.

Avec les lois que nous avons énoncées jusqu'à présent, nous sommes en mesure d'étudier certains régimes variables. En effet, tous les raisonnements basés sur la notion d'un champ (électrique ou magnétique) constant au cours du temps peuvent aisément être appliqués à des systèmes physiques variables (champs dépendant du temps), pourvu que cette variabilité s'effectue sur des échelles de temps longues par rapport au temps caractéristique d'ajustement du champ. Voici tout de suite un exemple concret:

La plupart des lois de la magnétostatique supposent un courant permanent, c'est-à-dire le même dans tout le circuit. Lorsque nous fermons un interrupteur, un signal électromagnétique se propage dans tout le circuit et c'est ainsi que peut s'établir un courant permanent: cela prend un temps de l'ordre de l/c où l est la taille du circuit et c la vitesse de la lumière. Si nous avons maintenant un générateur de tension sinusoïdale de période T (c'est juste un exemple... pris au hasard...), alors nous pourrons malgré tout utiliser les relations déduites de la magnétostatique si:

  (38.94)

Ainsi, bien que le courant soit variable, la création d'un champ magnétique obéira à la loi de Biot-Savart tant que le critère ci-dessus reste satisfait. Ce type de régime variable est appelé "régime quasi statique" dans le sens qu'il est transitoire.

Donc, puisque nous avons:

et   (38.95)

Nous avons alors si et seulement si le courant est variable dans le circuit:

  (38.96)

L étant constant pour un circuit rigide. La self ("inductance" en français) crée donc une force électromotrice inverse de celle générée par le courant à ses bornes. Cette force électromotrice a donc un sens inverse à celle du générateur électrique.

Dans le cas où une inductance est seule en série avec un générateur à courant alternatif sinusoïdal (cas assez typique dans le monde industriel du 19ème et 20ème siècle), alors la conservation du champ donnera:

  (38.97)

Et donc explicitement:

  (38.98)

Et donc:

  (38.99)

Pour avoir le courant, nous intégrons:

  (38.100)

Donc dans ce cas particulier, le courant est en retard sur la tension (ou la tension est en avance sur le courant) d'un quart de période. Il est par ailleurs d'usage de noter:

  (38.101)

Soit:

  (38.102)

où par analogie avec la résistance pure, l'expression:

  (38.103)

est appelée "réactance inductive".

Il convient de donner maintenant un exemple important et simple à la fois de la loi de Lenz en l'appliquant au calcul de l'inductance d'un solénoïde de rayon r (l'inductance d'un solénoïde torique à section circulaire ayant déjà été mise en évidence dans le chapitre de Magnétostatique). Nous avons vu dans le chapitre de Magnétostatique que le champ magnétique dans un solénoïde était donné par:

  (38.104)

où pour rappel N est le nombre de spires et l est la longueur du solénoïde. Nous avons vu plus haut que la loi de Faraday était donnée par:

  (38.105)

et dans le cas d'une spire nous allons parcourir N fois le chemin de l'intégrale. Il vient alors:

  (38.106)

Nous avons vu plus haut que le flux du champ magnétique était donné par (si le champ est perpendiculaire à la surface traversée):

  (38.107)

Dès lors:

  (38.108)

Le taux de variation du flux magnétique se trouve par dérivation, soit:

  (38.109)

Soit dans le cas de spires circulaires:

  (38.110)

La force électromotrice engendrée est ainsi:

  (38.111)

et donc par correspondance:

  (38.112)

Calculons maintenant la puissance reçue par une bobine. Nous avons démontré plus haut que nous avons toujours dans notre cas d'étude et si nous modélisons l'inductance comme un dipôle non idéal:

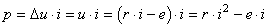  (38.113)

où les lettres en minuscules indiquent que nous sommes en régime non constant:

  (38.114)

Contrairement au développement que nous avions fait dans le chapitre d'Électrostatique pour le même calcul en ce qui concerne la capacité, nous n'avons pas négligé ici la dissipation d'énergie par effet Joule. Mais il faut savoir que dans la majorité des cas ce terme est aussi négligé!

Donc par intégration dans un intervalle de temps donné de 0 à t nous avons pour le deuxième terme:

  (38.115)

Soit explicitement dans le cas d'un solénoïde circulaire:

  (38.116)

Lorsque i décroit, la bobine restitue cette énergie. Nous ne pouvons donc pas stocker de l'énergie dans une bobine isolée contrairement à un condensateur.

Dans le cadre d'un régime sinusoïdal, la puissance moyenne sera nulle. Nous pouvons généraliser ceci en admettant qu'une inductance parfaite ne dissipe aucune puissance par effet Joule.

EFFET DE PEAU

L'effet de peau ou effet pelliculaire (ou plus rarement effet Kelvin) est un phénomène électromagnétique qui fait que, à fréquence élevée, le courant a tendance à ne circuler qu'en surface des conducteurs. Ce phénomène d'origine électromagnétique existe pour tous les conducteurs parcourus par des courants alternatifs. Il provoque la décroissance de la densité de courant à mesure que l'on s'éloigne de la périphérie du conducteur. Il en résulte une augmentation de la résistance du conducteur.

Cet effet peut être utilisé pour alléger le poids des lignes de transmission à haute fréquence en utilisant des conducteurs tubulaires, ou même des tuyaux, sans perte de courant. Il sert aussi dans le blindage électromagnétique des fils coaxiaux en les entourant d'un mince étui métallique qui garde les courants induits par les hautes fréquences ambiantes sur l'extérieur du câble.

Ce que nous souhaiterions déterminer maintenant, c'est l'atténuation du champ électrique (ou un coefficient d'atténuation) dans la matière d'un câble conducteur cylindrique plein en fonction de la distance de son axe de symétrie longitudinal à sa surface extérieure..

Pour cela, nous reprenons la quatrième équation de Maxwell sous la forme donnée précédemment:

  (38.117)

et que nous supposons travailler avec un conducteur n'ayant pas d'effet capacitif (donc pas de courant de déplacement) à l'opposé du cas général démontré dans le chapitre d'Électrodynamique, cette dernière se réduit alors à:

  (38.118)

et si nous l'associons à la troisième équation de Maxwell (cf. chapitre Électrodynamique) qui est pour rappel:

  (38.119)

Nous avons alors en utilisant le théorème de Schwarz (cf. chapitre de Calcul Différentiel Et Intégral):

  (38.120)

Or nous avons démontré dans le chapitre de Calcul Vectoriel qu'en toute généralité le rotationnel du rotationnel d'un champ vectoriel est égal au gradient de la divergence de ce champ moins son laplacien vectoriel:

  (38.121)

Or comme la divergence du champ électrique est nulle à travers la section d'un conducteur nous avons:

  (38.122)

d'où:

  (38.123)

Ce qui donne explicitement pour une composante (par exemple en z):

  (38.124)

Plaçons-nous dans le cas important d'un régime harmonique:

  (38.125)

et utilisons temporairement la notation en phaseurs:

  (38.126)

Nous avons alors

  (38.127)

Nous obtenons alors l'équation différentielle suivante à une variable:

  (38.128)

Soit:

  (38.129)

et donc:

  (38.130)

en se rappelant (cf. chapitre Nombres) que:

  (38.131)

il vient:

  (38.132)

Dès lors:

  (38.133)

Donc:

  (38.134)

Nous devons rejeter pour des raisons physiques (conservation de l'énergie) la solution:

  (38.135)

Il nous reste donc:

  (38.136)

que  les physiciens notent:

  (38.137)

car  se mesure en mètres (coefficient qui est nul si le champ électrique est constant) et est assimilé au "coefficient d'atténuation" que nous nous étions fixé de déterminer au début:

  (38.138)

Pour un conducteur en cuivre, nous avons selon Wikipédia les valeurs ci-dessous.

SEMI-CONDUCTEURS

Le défaut principal du modèle de Drude vu précédemment est de considérer l'électron comme une particule classique. Un ensemble de telles particules n'est évidemment pas soumis aux distributions quantiques et donc à une relation explicite de la température.

De plus, si nous observons notre modèle de Drude, il est difficile de dire quoi que ce soit à propos de la résistivité en fonction de la température.

Au fait, nous retenons en général quatre dates à la source du développement de cette théorie des semi-conducteurs:

- En 1833, Michael Faraday fait état de la conductivité d'un matériau qui augmente avec la température.

- En 1839, Antoine Becquerel découvre que sous illumination une tension électrique apparaît à la jonction de certains matériaux (et liquides). C'est l'effet photovoltaïque, qui donnera naissance beaucoup plus tard (vers 1950) aux cellules solaires.

- En 1873, Willoughby Smith montre que la conductivité de certaines substances augmente lorsque qu'on les illumine. C'est la photoconductivité.

- Enfin, en 1874 Karl Ferdinand Braun découvre le phénomène de redressement électrique lorsqu'une pointe métallique est déposée sur certains conducteurs, c'est-à-dire que le courant électrique passe dans un sens lorsque le potentiel électrique appliqué à la pointe est positif mais non lorsqu'il est négatif!

Bien que ces découvertes fussent totalement incomprises et surtout non reconnues comme étant les différentes expressions d'un même phénomène physique (la semi-conductivité), les applications pratiques furent immédiates et menèrent à la deuxième révolution industrielle qui est celle de la microélectronique!

Ce type de difficulté (parmi de nombreuses autres...) s'efface en grande partie avec le modèle de l'électron libre dans un puits de potentiel, imaginé par Sommerfeld en 1928. Dans ce modèle les électrons, soumis au principe de Pauli, suivent la distribution en énergie de Fermi-Dirac (cf. chapitre de Mécanique Statistique), alors que dans le modèle de Drude ils suivaient la loi de Maxwell-Boltzmann.

Il en découle deux résultats importants:

- Seule une fraction des électrons est susceptible de voir son énergie varier sous l'effet d'une action extérieure (température, champ électrique, etc.)

- Même au zéro absolu, l'énergie cinétique des électrons n'est pas nulle.

Le modèle de Sommerfeld fournit une base pour l'édification de théories plus spécifiques et est à la base du domaine de la "physique du solide" selon certaines sources. Ce n'est donc pas un modèle achevé traitant d'un problème précis comme la conduction électrique ou l'émission thermoélectronique. Cette base est la distribution en énergie des électrons, obtenue par le produit de deux fonctions: la densité des états et la distribution de Fermi-Dirac.

Malgré les améliorations qu'il apporte, ce modèle ne donne cependant pas une description satisfaisante des propriétés électroniques des solides dans tous les cas. Ses limitations proviennent du fait qu'il ne tient pas compte implicitement de la structure réelle des matériaux et des interactions entre électrons. Ce modèle ne permettra donc jamais d'expliquer objectivement pourquoi tel cristal est conducteur, et tel autre isolant ou semi-conducteur (par exemple le diamant et le silicium ont la même structure cristalline et configuration électronique mais à partir d'une certaine température l'un devient conducteur et l'autre reste isolant!).

La théorie des semi-conducteurs, appelée plus souvent "théorie des bandes" pour des raisons que nous verrons plus loin, est aussi un exemple fameux de l'application des résultats de la physique quantique ondulatoire (voir chapitre du même nom) et de la statistique quantique (cf. chapitre de Mécanique Statistique).

Pour son étude, nous nous concentrerons ici sur le modèle scolaire qualitatif le plus simple qui est celui basé sur un semi-conducteur cristallin avec un réseau parfaitement périodique et à bandes paraboliques (nous préciserons cela à nouveau plus loin).

Le lecteur un peu critique verra que les développements qui vont suivre ne sont cependant pas purement quantiques (il y a même des développements utilisant la mécanique classique qui sont limites acceptables suivant le point de vue)... donc l'approche est un peu grossière mais elle permet d'avoir une idée qualitative des phénomènes dans les semi-conducteurs. C'est une des raisons pour laquelle ce modèle est appelé "modèle semi-classique des bandes paraboliques".

Au fur et à mesure des années nous compléterons les développements qui vont suivre pour au final tenter d'avoir toute la démarche détaillée. D'ici là il faudra être patient...

Nous ferons abstraction des concepts qui ne sont pas absolument nécessaires à l'introduction du modèle pour présenter ici uniquement l'essentiel qui suffit à l'ingénieur dans son travail quotidien.

Pour commencer la partie mathématique de l'étude des semi-conducteurs, nous considérerons un cristal soumis à une différence de potentiel. Un électron de conduction du cristal sera donc soumis d'une part à une force interne  résultant du champ cristallin, et d'autre part à une force d'origine externe  résultant du champ électrique appliqué au cristal.

Les hypothèses du modèle sont:

H1. Il existe à la surface des métaux une barrière de potentiel empêchant les électrons de quitter la matière.

H2. À l'intérieur de la matière, les électrons sont soumis à un potentiel constant!

H3. Les électrons sont indépendants (pas d'interactions entre eux).

H4. Les électrons obéissent aux lois de la mécanique quantique et classique.

H5. Les électrons obéissent aux lois de l'électrodynamique de Maxwell.

H6. Les bandes d'énergie forme un spectre continu de niveaux d'énergie.

La première hypothèse repose sur l'observation élémentaire suivante: les électrons se déplaçant dans un métal ne franchissent pas, à température ambiante tout au moins, les surfaces limitant l'échantillon.

La deuxième hypothèse paraît assez brutale. C'est elle qui bannit du modèle la notion de structure de la matière. Elle sera remplacée dans le modèle des bandes d'énergie par un potentiel périodique rendant compte de l'influence des noyaux chargés positivement. Cette hypothèse traduit le fait que les électrons sont considérés comme libres dans le puits de potentiel.

La barrière de potentiel possède une largeur finie, c'est-à-dire que le passage du potentiel régnant à l'intérieur de la matière au potentiel régnant à l'extérieur se fait sur quelques distances interatomiques. Mais les dimensions de l'échantillon étant en pratique toujours très grandes vis-à-vis d'une distance interatomique, on peut considérer la barrière de potentiel comme infiniment abrupte, ce qui simplifie les calculs.

L'équation de la dynamique s'écrit alors naturellement pour cet électron:

  (38.139)

Nous écrivons alors (rien ne nous interdit de le faire) que l'électron dans le cristal répond à la sollicitation de la force externe  comme une quasi-particule de masse  dans le vide:

  (38.140)

C'est l'étude de ce dernier terme qui va nous intéresser. Pour cela rappelons que dans le cadre de l'étude détaillée de la propagation de l'électron libre dans le vide, où nous négligeons les effets de son spin, nous avons démontré qu'il doit obligatoirement être décrit selon l'équation de Schrödinger par un paquet d'onde (cf. chapitre de Physique Quantique Ondulatoire) centré sur un état  sinon quoi son énergie serait infinie.

On peut cependant se poser la question... de ce qui nous amène à le considérer comme libre.... Eh bien c'est l'expérience qui montre que lorsque nous appliquons un certain potentiel seuil, un courant commence à apparaître dans les semi-conducteurs.

Nous avons démontré (toujours dans le cadre de la propagation de la particule libre sans spin dans le chapitre de Physique Quantique Ondulatoire) que le paquet d'onde peut alors être vu dans sa solution mathématique comme une onde plane (libre) se déplaçant à la vitesse de phase:

  (38.141)

que nous noterons pour la suite afin de simplifier les notations:

  (38.142)

Or, dans le réseau cristallin, la vitesse de phase peut varier, en fonction de l'endroit du réseau où se trouve l'électron à cause de la forme géométrique du potentiel dans le cristal. Il nous faut donc utiliser la vitesse de phase instantanée:

  (38.143)

Rappelons que nous avons aussi en toute généralité l'énergie totale donnée par:

  (38.144)

Il vient alors:

  (38.145)

Le terme:

  (38.146)

n'est de loin pas simple dans le cas d'un cristal (c'est même un cauchemar...).

Évidemment pour une particule libre (cf. chapitre de Physique Quantique Ondulatoire), rappelons qu'il s'agit de:

  (38.147)

Mais pour une particule dans un champ de potentiel ayant une géométrie complexe l'énergie E commence à avoir une expression dépendante de k en fonction des zones qui peut devenir très complexe (voir les exemples du chapitre de Physique Quantique Ondulatoire). D'où la justification de l'utilisation de la dérivée.

L'accélération au sens classique de cet électron est alors donnée par:

  (38.148)

Nous avons aussi (cf. chapitre de Mécanique Classique):

  (38.149)

donc:

  (38.150)

d'où:

  (38.151)

La dérivée de  par rapport à  dans la relation précédente s'annulera car la force découle du potentiel appliqué sur le semi-conducteur seulement et non pas du vecteur d'onde de l'électron lui-même! Il nous reste alors:

  (38.152)

Puisque ici E est uniquement l'énergie totale provenant du potentiel soumis de l'extérieur, alors la force  est la force externe  générée par l'application de ce même potentiel. Nous avons alors:

  (38.153)

et:

  (38.154)

Il vient alors par égalisation:

  (38.155)

Puisque l'énergie de l'électron peut avoir une forme mathématique compliquée conformément aux cas applicatifs vus dans le chapitre de Physique Quantique Ondulatoire, exprimons  sous forme de développement limité de Taylor (cf. chapitre de Suites et Séries) d'une fonction à trois variables au deuxième ordre en laissant tomber les termes d'interactions et en en ne prenant pas les termes de premier degré:

  (38.156)

Au fait cette approximation grossière mais toutefois acceptable dans pas mal de cas pratiques tient au fait que l'expérience montre que les surfaces d'énergie en fonction de k ont en approximation une forme parabolique dans certains cristaux semi-conducteurs.

Dans les conducteurs, l'approximation de la relation précédente n'est prise qu'au premier terme.

 Une autre manière de le voir est que pour un électron libre, nous avons pour rappel, en une dimension, la courbe de dispersion (cf. chapitre de Physique Quantique Ondulatoire):

  (38.157)

qui est bien une parabole en fonction de k. Effectivement, si nous prenons notre développement de Taylor en une dimension il  nous reste:

  (38.158)

et comme nous avons déterminé avant que:

  (38.159)

Il vient:

  (38.160)

Si l'électron est libre la courbe de dispersion nous impose d'avoir (sans présence de potentiel):

  (38.161)

qui est alors considérée comme "l'énergie du minimum"  Il nous reste alors:

  (38.162)

et en prenant  nous retombons sur courbe de dispersion d'une particule libre (ce qui justifie donc le fait d'avoir posé  pour un électron libre):

  (38.163)

Ce qui montre que l'approximation n'est pas trop fausse... et justifie le fait que dans certains ouvrages la relation précédente (série de Taylor) décrit une particule dite "quasi-libre".

Mais revenons-en à:

  (38.164)

Et puisque le paquet d'onde est centré autour de  normalisons-la comme valant 0 (ce qui équivaut à centrer les valeurs du vecteur d'onde). Nous avons alors:

  (38.165)

Ce qui est intéressant avec ces développements, c'est que nous sommes partis d'un électron libre sous forme de paquet d'onde et grâce au développement de Taylor nous nous retrouvons avec une expression extrêmement simple de l'énergie d'un électron quasi-libre.

Il en sort que pour un électron quasi-libre, sans interactions et sans prendre en compte les effets de spin nous avons:

  (38.166)

Nous remarquons alors une chose fort sympathique! C'est que notre électron quasi-libre a un nombre d'onde qui ressemble en tout point à celui d'une particule coincée dans un puits de potentiel à parois rectilignes (voir la démonstration dans le chapitre de Physique Quantique Ondulatoire).

Nous souhaiterons maintenant calculer à l'aide de l'expression de k (n'ayant pas directement celle de E car trop complexe) la densité d'états (in extenso d'électrons) dans le volume donné par le puits rectangulaire correspondant.

Nous avons démontré dans le chapitre de Physique Quantique Ondulatoire que pour le puits de potentiel à barrières rectangulaires:

  (38.167)

si nous imposions un nombre entier de demi-longueur d'onde. Si nous imposons un nombre entier de longueur d'onde (conditions de Born-von Karman afin qu'après une translation du réseau périodique du cristal nous retrouvions les mêmes propriétés) pour que la solution soit physiquement acceptable, nous avons alors:

  (38.168)

ce qui implique bien évidemment deux fois moins d'états.

Par extension, pour l'espace, nous avons alors dans le cas tridimensionnel:

  (38.169)

avec:

  (38.170)

et où

Le résultat est très similaire à celui du puits de potentiel rectangulaire à une dimension mais nous avons maintenant des conditions aux bords particulières afin d'avoir une correspondance avec l'expérience et trois nombres quantiques principaux au lieu d'un seul. De plus, chaque combinaison de ces trois nombres correspond à une fonction d'onde (état) différente. De plus, ces nombres sont indépendants (aucune condition imposée).

Nous avons alors le premier niveau où tous les n sont unitaires:

  (38.171)

Si nous acceptons pour simplifier que le puits a des arêtes de longueurs égales (semi-conducteur à réseau cristallin cubique), nous avons alors:

  (38.172)

Représentons l'espace des k pour un tel réseau cubique et pour différents multiples de :

Figure: 38.2 - Espace des k pour un réseau cristallin cubique

Donc tous les états quantifiés ne peuvent prendre que des valeurs espacées de  dans l'espace des k ce qui signifie que par volume élémentaire il n'y a qu'un seul vecteur d'onde possible et donc qu'un seul état associé. Effectivement, faites un dessin par-dessus la figure ci-dessus si vous voulez et vous verrez (!) mais ne vous fiez pas aux gros points noirs qui sont là uniquement pour montrer les extrémités des volumes élémentaires et qui ne correspondent pas tous à des états possibles!

Ainsi, dans un volume sphérique de rayon k de l'espace des k. Nous avons un nombre précis (limite supérieure) de volume élémentaires (états):

  (38.173)

où dans la littérature il est d'usage (tradition) de ne conserver que la forme de la deuxième égalité dans les développements. Cette relation nous a été pour rappel utile dans le chapitre de Thermodynamique pour déterminer le modèle de Debye-Einstein de la capacité thermique à volume constant des solides cristallins!

La densité de modes dans un volume V sera alors donné par (relation utilisée dans le chapitre de Thermodynamique pour exprimer la capacité calorifique à volume constant des solides):

  (38.174)

Remarque: La sphère de rayon k, contenant les niveaux à un électron qui sont occupés est appelée parfois "sphère de Fermi". La valeur du rayon est alors notée  et appelée "vecteur d'onde de Fermi". La surface de la sphère de Fermi, qui sépare les niveaux occupés de ceux qui ne le sont pas comme nous le verrons plus tard est appelée "surface de Fermi".

En considérant maintenant le spin (ben oui tant qu'on y est...) nous multiplions par 2 puisqu'il y a deux états de spin possible par état:

  (38.175)

(relation que nous retrouverons dans le chapitre de Physique Nucléaire lors de notre étude du modèle de noyau nucléaire sous forme de goutte liquide) et en y injectant:

  (38.176)

nous avons alors:

  (38.177)

La densité volumique d'états (quasi-)libres sera obtenue en dérivant cette dernière relation par le volume:

  (38.178)

Et si nous souhaitons la densité d'états (quasi-)libres (de vibration) par unité d'énergie et de volume il va nous falloir en plus dériver par rapport à l'énergie:

  (38.179)

Ce qui donne:

  (38.180)

Ce résultat ne dépendant pas du volume, il est inchangé lorsque celui-ci tend vers l'infini! Donc il est valable pour tout point du cristal semi-conducteur si celui-ci est parfait...

Ce que nous trouvons également parfois sous les formes (un peu malheureuses...) suivantes dans certains ouvrages:

  (38.181)

et il y aussi ceux qui ne prennent en compte le spin que plus tard... ce qui donne une forme identique à celle des trois relations précédentes mais à diviser par 2.

DENSITÉ STATISTIQUE NON-DÉGÉNÉRÉE DES PORTEURS NÉGATIFS

Bref, cependant cette relation a un défaut (encore un...)! Effectivement, nous avons vu dans le chapitre de Mécanique Statistique lors de notre étude de la statistique quantique que dans un système où même le spectre d'énergie est considéré comme continu, il est impossible de ne pas prendre en compte la dégénérescence des différents niveaux d'énergie. Nous avions démontré alors que pour une population de fermions, à une énergie (ou température) donnée le pourcentage de niveaux dégénérés occupés est donné par la fonction de Fermi-Dirac:

  (38.182)

et que la fonction retournait donc une valeur comprise entre 0 au minimum et 1 au maximum.

Cette fonction donne donc pour une température T fixée la probabilité qu'un électron occupe un état d'énergie E.

Ce qui fait que notre relation D(E) surestime la valeur réelle de densité d'états (quasi-)libres occupés pour une énergie (ou température) donnée. Ce qui fait que pour avoir une meilleure approximation nous écrivions en toute logique la densité volumique d'états (quasi-)libres par unité d'énergie:

  (38.183)

Cependant, dans la pratique, nous allons chercher à calculer la densité volumique d'états (quasi-)libres dans un spectre (intervalle) d'énergie. Il vient alors avec la correction ajoutée précédemment:

  (38.184)

Soit:

  (38.185)

Il vient alors immédiatement que la densité volumique d'états (d'électrons) (quasi-)libres à une température donnée (conditions normales de température pour les applications civiles) en prenant en compte tous les états (niveaux continus) d'énergie possibles est alors:

  (38.186)

Prendre  comme borne inférieure nous évite, comme nous allons le voir explicitement un peu plus bas, de nous retrouver avec une racine négative... ce qui serait fort gênant!

De plus, nous pouvons sans erreur appréciable reporter la limite de l'intégrale à l'infini car  quand E est importante.

Malheureusement, cette intégrale n'est en général pas soluble analytiquement. Il va donc falloir recourir à des approximations.

Nous allons commencer par faire l'hypothèse que nous sommes dans le régime classique du gaz d'électrons. C'est-à-dire que le terme:

  (38.187)

ce qui implique:

  (38.188)

Dès lors, nous avons aussi l'approximation:

  (38.189)

En d'autres termes l'énergie E doit être bien supérieure au potentiel chimique  (assimilé souvent malheureusement et à ma connaissance à tort dans la littérature sur les semi-conducteurs au niveau de Fermi ). Les physiciens notent alors cette énergie  pour la distinguer et l'appellent "énergie minimale de la bande de conduction" (qui correspond à l'énergie minimale d'un électron quasi-libre pour satisfaire cette condition).

Dès lors, nous changeons aussi la notation pour la densité de charge:

  (38.190)

Nous avons alors:

  (38.191)

Où  est la fonction de Maxwell-Boltzmann (cf. chapitre de Mécanique Statistique) donnée pour rappel par:

  (38.192)

Et correspond donc bien à un comportement non quantique (soit un gaz d'électrons non-dégénéré!) car lorsque:

  (38.193)

nous avons:

  (38.194)

et donc les états d'énergie ne sont de loin pas tous occupés par les électrons (il n'y a donc pas dégénérescence).

Nous sommes donc bien dans une situation où la physique classique prédomine sur la physique quantique. C'est la raison pour laquelle dans cette approximation (de Maxwell-Boltzmann) nous disons alors que nous avons affaire à un "semi-conducteur non-dégénéré" car les électrons ne sont pas entassés dans les niveaux les plus bas disponibles.

Pour pouvoir continuer, nous faisons un changement de variable en posant:

  (38.195)

d'où:

  (38.196)

Il vient alors:

  (38.197)

Nous faisons une intégration par parties:

  (38.198)

nous faisons ensuite un changement de variable en posant:

  (38.199)

Ce qui donne:

  (38.200)

Nous avons déjà calculé cette intégrale dans le chapitre de Statistiques. Il vient:

  (38.201)

Nous avons alors finalement:

  (38.202)

Où pour rappel,  est la masse de la quasi-particule (et non la masse de l'électron pour rappel!). Donc après intégration tout se passe comme si tous les électrons étaient concentrés sur le niveau d'énergie  avec un nombre de places disponibles correspondant à:

  (38.203)

Ce que nous notons traditionnellement (et de manière un peu malheureuse... car il n'est pas évident de se rappeler qu'il s'agit d'une densité):

  (38.204)  

Ou encore:

  (38.205)

Où nous avons environ à température ambiante (c'est le paramètre de la masse effective qui varie entre les deux) les valeurs suivantes d'états (quasi-)libres respectives pour le Silicium:

  (38.206)

Et pour le Germanium:

  (38.207)

Alors qu'il y a environ une densité d'atomes de  et environ  électrons pour ces deux éléments.

Cela signifie qu'il y a donc un rapport de 1/100000 entre la densité d'électrons totale et le nombre d'électrons quasi-libres.

Nous remarquons cependant également que ce modèle théorique ne prend pas en compte la structure électronique (numéro atomique) du matériau étudié.

Ainsi, nous voyons que les variations des densités d'électrons quasi-libres en fonction de la température (dans la gamme de validité de la température...) sont essentiellement de type exponentiel croissant ou décroissant.

À partir de la densité des électrons libres (attention il faut bien se rappeler que ce sont uniquement les électrons quasi-libres qui se baladent dans nos équations mathématiques jusqu'à maintenant) dans le cristal semi-conducteur, nous pouvons en déduire l'énergie du niveau de Fermi (plus rigoureusement il s'agit du potentiel chimique!):

  (38.208)

d'où:

  (38.209)

Et puisque  nous avons toujours à cause du logarithme qui est négatif, l'énergie de Fermi (plus rigoureusement il s'agit du potentiel chimique!) qui est inférieure ou égale à l'énergie des électrons quasi-libres:

  (38.210)

Ou en d'autres termes, les électrons (quasi-)libres ont une énergie supérieure à l'énergie de Fermi (potentiel chimique...) ce qui est conforme à l'approximation du gaz non dégénéré faite plus haut. Cela donne une condition d'importance capitale pour que les porteurs négatifs puissent être les générateurs de la conduction dans le matériau.

Ainsi, lorsque nous nous plaçons à une température différente du zéro absolu, les états électroniques ne sont pas tous dégénérés: il y a étalement des états occupés au voisinage de ce qui constitue par définition l'énergie de Fermi (cf. chapitre de Mécanique Statistique et Physique Quantique Ondulatoire), effet d'autant plus accentué que la température est élevée.

DENSITÉ STATISTIQUE NON-DÉGÉNÉRÉE DES PORTEURS POSITIFS

Avant toute chose, il faut savoir que dans l'état actuel de nos connaissances les "trous" n'émergent pas des équations mais sont une construction empirique qui permet de faire correspondre la théorie et l'expérience (charges positives de l'effet Hall par exemple). Il s'agit donc d'un artifice pour faire une théorie simple d'une question intraitable rigoureusement à notre époque par la physique quantique.

Personnellement, je considère les trous de la même manière que les points de Lagrange en astronomie: Même s'il n'y a aucun corps en ces points de Lagrange cela n'empêche pas un satellite de se mettre en orbite (quasi-stable) autour de ceux-ci (possibilité que nous n'avons pas démontrée dans le chapitre d'Astronomie) comme s'il y avait une masse! Par ailleurs des expériences auraient montré au début des années 2000 que des points de Lagrange apparaissent au niveau de l'atome dans certaines conditions idéales et simplifiées!

Ceci dit, il faut se rappeler qu'un trou n'est pas un électron qui manque! C'est une idiotie (selon moi...) que l'on voit dans certains ouvrages spécialisés.

Au risque de se répéter un peu souvent, rappelons que pour une température T fixée la probabilité qu'un électron occupe un état d'énergie E est donnée par:

  (38.211)

Ce qui fait que pour avoir une meilleure approximation, nous écrivions en toute logique la densité volumique d'états occupés par unité d'énergie:

  (38.212)

Ce qui nous a amené finalement à la relation suivante de la densité volumique d'états de charges négatives où la présence d'une masse dans la relation indique que les états occupés le sont par des quasi-particules telle que:

  (38.213)

Mais qu'en est-il de la probabilité qu'un électron n'occupe pas pour une température T fixée un état d'énergie E et trivialement donnée par la différence:

  (38.214)

où le n en indice est là pour indiquer que la distribution concerne les porteurs "négatifs" (distribution donnée comme nous l'avons démontré juste précédemment par la distribution de Maxwell-Boltzmann qui découle d'une approximation de la loi de Fermi-Dirac).

Eh bien nous allons constater que les équations nous conduisent à la possibilité d'associer aussi à ces états non occupés une densité volumique d'états avec une masse effective donnée. Nous verrons aussi plus tard qu'il sera possible d'associer à ces états non occupés une charge électrique positive et égale et à celle de l'électron, d'où le p en indice dans le relation précédente et signifiant "positif".

Nous avons donc pour ces porteurs positifs:

  (38.215)

faisons maintenant une approximation similaire à celle utilisée pour les porteurs négatifs, c'est-à-dire que:

  (38.216)

pour imposer un régime semi-classique et donc les états d'énergie ne sont de loin pas tous occupés par les trous (il n'y a donc pas dégénérescence).

Cette restriction impose:

  (38.217)

Soit écrit de la même manière que pour les porteurs négatifs:

  (38.218)

Soit contrairement aux porteurs négatifs cela impose:

  (38.219)

en d'autres termes l'énergie doit être bien inférieure au niveau de Fermi (potentiel chimique). Les physiciens notent alors cette énergie  pour la distinguer et l'appellent "énergie maximale de la bande de valence" (qui correspond à l'énergie maximale d'un trou quasi-libre pour satisfaire cette condition).

Nous avons alors:

  (38.220)

Dès lors, nous avons aussi l'approximation:

  (38.221)

Nous sommes donc bien dans une situation où la physique classique prédomine sur la physique quantique. C'est la raison pour laquelle dans cette approximation nous disons que nous avons alors affaire à un "semi-conducteur non-dégénéré" car les trous ne sont pas entassés dans les niveaux les plus hauts disponibles.

Nous avons alors:

  (38.222)

où le lecteur aura pu observé que les bornes d'intégration ont été choisies conformément à la remarque que nous avions faite juste précédemment et que les termes dans la racine carrée ont été permuté afin de ne pas y avoir de valeur négative.

Pour pouvoir continuer, nous faisons un changement de variable en posant:

  (38.223)

d'où:

 et   (38.224)

Il vient alors:

  (38.225)

Nous faisons une intégration par parties:

  (38.226)

nous faisons ensuite un changement de variable en posant:

  (38.227)

Ce qui donne:

  (38.228)

Nous avons déjà calculé cette intégrale dans le chapitre de Statistiques. Il vient (puisque la fonction est paire nous utilisons la propriété démontrée dans le chapitre de Calcul Différentiel Et Intégral):

  (38.229)

Nous avons alors finalement:

  (38.230)

où pour rappel,  est la masse de la quasi-particule (et non la masse du trou pour rappel!). Donc après intégration tout se passe comme si tous les trous étaient concentrés sur le niveau d'énergie  avec un nombre de places disponibles correspondant à:

  (38.231)

Ce que nous notons traditionnellement (et de manière un peu malheureuse... car il n'est pas évident de se rappeler qu'il s'agit d'une densité):

  (38.232)

ou encore:

  (38.233)

où nous avons environ à température ambiante (c'est le paramètre de la masse effective qui varie entre les deux) les valeurs suivantes d'états (quasi-)libres respective pour le Silicium:

  (38.234)

et pour le Germanium:

  (38.235)

BANDES D'ÉNERGIE

Les développements précédents pour les porteurs négatifs et positifs nous ont montré que dans le cadre de l'approximation d'un gaz de fermions non dégénéré, l'énergie des porteurs négatifs doit se trouver bien au-dessus du niveau de Fermi (potentiel chimique) et l'énergie des porteurs positifs bien en-dessous.

C'est donc comme s'il y avait un intervalle d'énergie interdit ou ni électrons, ni trous n'ont droit de se situer! Cet intervalle d'énergie est traditionnellement appelé "bande d'énergie interdite" ou plus simplement "bande interdite" et abrégée B.I.

L'intervalle d'énergie interdit est quant à lui souvent appelé "gap" et est noté .

Voyons ceci sous forme schématique grossière en prenant garde au fait que ce schéma est donc quelque peu trompeur car il donne l'impression que la bande de conduction ou de valence occupe tout un bloc, alors qu'en réalité la bande de valence est constituée par la dernière couche complètement remplie, la bande d'énergie permise qui la suit étant appelée "bande de conduction".

Figure: 38.3 - Représentation des structures de bandes dans différents métaux

De plus, sachant que la chimie moléculaire permet de démontrer que des structures sont composées de multiples bandes (en fonction du premier et deuxième nombre quantique) il vient alors les définitions rigoureuses suivantes:

D1. La "bande de conduction" (notée BC) d'une structure solide est la bande de plus basse énergie partiellement occupée ou vide (sachant que d'autres bandes se situent au-dessus en termes énergétiques mais ne se rempliront que sous des températures élevées et n'existent que par une description théorique lorsqu'elles sont vides).

D2. La "bande de valence" (notée BV) d'une structure solide est la bande de plus haute énergie saturée, c'est-à-dire dont tous les états sont occupés (sachant qu'il peut y avoir en-dessous de la couche supérieure de la BV de multiples bandes en termes énergétiques et toutes saturées).

Nous avons également l'association schématique traditionnelle des bandes de conduction et de valence avec la fonction de Fermi-Dirac (qui comme déjà mentionné en toute rigueur devrait être le potentiel chimique à température non nulle!) représentée sous forme simplifiée par:

Figure: 38.4 - Association structure de bande avec fonction de Fermi-Dirac

Mais au fait cette représentation, que nous retrouvons un peu partout dans certains ouvrages est relativement erronée... puisqu'en faisant une approximation semi-classique par la loi de Maxwell-Boltzmann il n'est plus question en toute rigueur de représenter la distribution sous forme de loi de Fermi-Dirac comme l'aura remarqué le lecteur attentif! Comme quoi il faut faire attention car la représentation traditionnelle de  dans le modèle semi-classique indiquerait qu'il y aurait des états occupés dans la bande interdite alors que si nous représentions la fonction de Maxwell-Boltzmann, nous verrions deux fonctions distinctes au-dessus et en-dessous de la bande interdite!!!

Et il faut se rappeler (!) que la figure ci-dessus (même si elle est assez fausse) représente conceptuellement un semi-conducteur non dégénéré suite aux approximations semi-classiques que nous avons faites dans nos développements en utilisant le modèle d'un gaz non dégénéré (approximation de Maxwell-Boltzmann) et qui imposait théoriquement:

  (38.236)

que de nombreux auteurs écrivent (à nouveau c'est malheureux mais c'est ainsi...):

  (38.237)

Donc il vient une autre définition possible du semi-conducteur non dégénéré: c'est celui où le niveau de Fermi (le potentiel chimique!) se situe dans la bande interdite et ce cas correspond au fonctionnement de la majorité des composants microélectroniques.

Voici quelques valeurs expérimentales pour des semi-conducteurs courants:

nous comprenons alors de suite au vu de ces chiffres pourquoi le diamant, à structure cristalline et atomique quasi-identique, est isolant alors que le Silicium devient lui conducteur!

Ce qui est intéressant pour les chercheurs, c'est de combiner des matériaux afin de jouer avec la largeur de  en fonction des besoins!

Par ailleurs, nous pouvons aussi conclure hâtivement... que ce qui différencie isolants et semi-conducteurs c'est la largeur de leur bande interdite.

Remarquons aussi que l'énergie nécessaire à un électron pour passer de la bande de valence à la bande de conduction peut lui être fournie par un rayonnement.  Dans le cas d'une absorption de lumière, l'énergie  d'un photon peut être suffisante pour cela tant que:

  (38.238)

À basse température, un tel processus est capable de rendre le matériau conducteur (technologie des télescopes spatiaux à basse température). Cette propriété est appelée la "photoconductivité".

Enfin, rappelons les deux relations obtenus plus haut:

  (38.239)

Le produit de ces deux densités possède une propriété très intéressante. Nous pouvons en effet remarquer qu'il est indépendant de la position du niveau de Fermi et appelé "densité intrinsèque":

  (38.240)

Par exemple, quelques valeurs de la racine carrée de la densité intrinsèque à 300 [K] sont données dans la table ci-dessous:

Nous remarquons aussi que la densité critique est fortement dépendant de la température. Ces valeurs de densités sont bien évidemment idéalisées, dans la réalité ces valeurs sont bien inférieures à cause des imperfections (impuretés résiduelles, défauts de cristallisation,…) qui perturbent localement la périodicité du potentiel et, de ce fait, introduisent des niveaux énergétiques qui peuvent être accessibles aux électrons. Par opposition avec les niveaux correspondant au matériau pur, nous parlerons de "niveaux extrinsèques".

LOI D'OHM (DES SEMI-CONDUCTEURS)

Nous avons démontré dans le cadre du modèle de Drude que la conductivité était donnée par:

  (38.241)

où n est pour rappel la densité de porteurs dans le matériau. Nous avons également démontré que le courant est inversement proportionnel à la conductivité selon la relation:

  (38.242)

Dans le cadre des développements faits plus haut nous avons vu que la densité n des porteurs  était donnée respectivement par les relations suivantes à un potentiel constant (hypothèse du modèle):

 et   (38.243)

où les masses relatives  des quasi-particules (porteur négatif ou porteur positif) ne sont pas nécessairement égales! Ainsi, nous avons donc la résistance qui peut être approchée par une relation de la forme:

  (38.244)

et nous vérifions aisément cette dépendance en représentant graphiquement:

  (38.245)

soit ln(R) en fonction de 1/T (la résistance ne dépend donc que de la température en théorie... à tension constante).

La vraie complexité tient au fait que beaucoup de termes sont dépendants de la température (le niveau de Fermi, le temps de libre parcours moyen, etc.) et du potentiel appliqué ce qui fait que dans la réalité les courbes obtenues ne sont de loin pas conformes à la théorie....!

Une application numérique montre que les densités de porteurs  et  augmentent donc très rapidement déjà à partir de la température ambiante! Ce qui est conforme à l'expérience avec les semi-conducteurs non-dégénérés car nous aurons alors la conductivité qui augmente tout aussi fortement ce qui implique une baisse rapide de la résistance!

La grande sensibilité de la conductivité de certains solides aux variations de température est à l'origine de nombreuses applications, tant pour les métaux conducteurs que pour les semi-conducteurs. C'est ce que nous appelons des "thermistances".

Enfin, indiquons que dans le cas du Silicium, nous avons  alors que l'énergie cinétique dû à l'agitation thermique (cf. chapitre de Mécanique des Milieux Continus) est donnée à température ambiante par:

  (38.246)

Or, nous avons vu précédemment que seuls les électrons dont l'énergie était voisine de celle du niveau de Fermi pouvaient participer à la conduction. Leur énergie cinétique valant alors:

  (38.247)

où  est la "vitesse de Fermi".

En égalisant les deux dernières relations:

  (38.248)

Il y a donc un rapport d'un facteur de 30 entre les deux énergies, soit en prenant la racine carrée, un rapport 5 entre les vitesses. Nous avons donc:

  (38.249)

Or, nous avons déjà vu lors de notre étude du modèle de Drude que la vitesse thermique nous amenait à un libre parcours moyen supérieur d'un ordre de grandeur (facteur 10) des distances interatomiques. Et ici nous avons donc un facteur 5 en plus!!!! Soit plus de 50 distances interatomiques! Le libre parcours moyen l d'un électron de conduction est donc beaucoup plus grand que celui que nous avions déterminé à partir du modèle classique de Drude. Ainsi, le libre parcours moyen ne semble pas dû aux collisions avec les ions du réseau mais elle est imputable aux imperfections du réseau: défauts de structure, atomes étrangers...

Un semi-conducteur parfait (pur), soit sans imperfections, tel que nous l'avons traité théoriquement jusqu'à maintenant est appelé un "semi-conducteur intrinsèque": il ne comporte donc aucune impureté et son comportement électrique ne dépend que de la structure du matériau. Ce comportement correspond à un semi-conducteur parfait, c'est-à-dire sans défaut structurel ou impureté chimique. Un semi-conducteur réel n'est jamais parfaitement intrinsèque, mais peut parfois en être proche comme le silicium monocristallin pur.

Dans un semi-conducteur intrinsèque, les porteurs de charge ne sont créés que par excitation thermique. Le nombre d'électrons dans la bande de conduction est alors égal au nombre de trous dans la bande de valence comme nous l'a montré notre modèle théorique.

Il faut savoir qu'en réalité ces semi-conducteurs ne conduisent pas, ou très peu, le courant, excepté si nous les portons à haute température.

- Physique des semiconducteurs et des composants électriques, H. Mathieu, Éditions Dunod
ISBN10: 2100486330 (826 pages) - Imprimé en 2004

4   1

Notée par 23 visiteur(s) 12345 PageRater 0.5.0 Commentaires: [0]