|

GÉNIE MARIN & MÉTÉO | GÉNIE
MÉCANIQUE | GÉNIE ÉLECTRIQUE
GÉNIE ÉNERGÉTIQUE | GÉNIE
CIVIL | GÉNIE BIOLOGIQUE | GÉNIE
AÉROSPATIAL
GÉNIE CHIMIQUE | GÉNIE INDUSTRIEL |
GÉNIE LOGICIEL
L'ingénierie est l'ensemble
des pratiques consistant à appliquer les résultats
des sciences exactes et de la recherche fondamentale à des
problèmes concrets, industriels ou quotidiens. (Larousse)
Dernière mise à jour de ce chapitre:
2017-12-31 17:59:46 | {oUUID 1.801}
Version: 3.0 Révision 6 | Avancement:
~70%
 vues
depuis
le 2012-01-01:
0 vues
depuis
le 2012-01-01:
0
 LISTE DES SUJETS TRAITÉS SUR CETTE PAGE
LISTE DES SUJETS TRAITÉS SUR CETTE PAGE
La météorologie
est l'étude des phénomènes
atmosphériques tels les nuages, les dépressions et
les précipitations
pour comprendre comment ils se forment et évoluent. C'est
une discipline qui traite principalement de la mécanique
des fluides appliquée
à l'air mais qui fait usage de différentes autres branches
de la physique et de la chimie. Elle permet donc d'établir
des prévisions
météorologiques en s'appuyant sur des modèles
mathématiques à court
comme à relativement long terme. Elle est également
appliquée
pour la prévision
de la qualité de l'air, pour les changements climatiques
et pour l'étude dans plusieurs domaines de l'activité humaine
(construction, trafic aérien, etc.)
La météorologie est liée à une grande
quantité de variables dont il serait très difficile
de faire une liste même non exhaustive... Cependant sur notre
planète Terre, un facteur important à ne pas négliger
est celui constitué par les surfaces océaniques et
leur dynamique intrinsèque dont nous tenterons de présenter
au travers d’une étude mathématique sommaire
quelques-unes de leurs propriétés.
Ce chapitre est une introduction générale de base
au domaine des applications techniques de la thermodynamique et
de la mécanique des fluides. Il permettra au lecteur de
se familiariser avec le langage et certaines méthodes de
calculs fondamentales utilisées par les ingénieurs
de cette branche. Bien sûr, il faut compléter cette étude
par des travaux pratiques en laboratoire.
HORIZON VISUEL
Étudions d'abord un petit sujet sympathique faisant souvent
débat lors des vacances ou plus sérieusement... Dans
certains logiciels de météorologie, il est demandé de
saisir la distance de l'horizon visuel lors de mesures de température
et pression... or celle-ci est difficile à déterminer
par très beau temps lorsque nous sommes en hauteur.
Pour cela, considérons
la Terre de rayon R et un point de perspective de hauteur h par
rapport au niveau de la mer que nous noterons A. La question
est de savoir à quelle distance se trouve le point C donné par
définition par la tangente AC qui est simplement
la ligne d'horizon.

Figure: 69.1 - Configuration de l'expérience...
Le lecteur observera déjà que l'étude va principalement faire
appel à de la trigonométrie et de la géométrie élémentaire.
L'angle 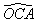 est
un angle droit. En effet, une droite tangente en un point d'un
cercle est perpendiculaire au rayon en ce point. Le triangle OCA est
donc rectangle en C. est
un angle droit. En effet, une droite tangente en un point d'un
cercle est perpendiculaire au rayon en ce point. Le triangle OCA est
donc rectangle en C.
Nous avons donc:
 (69.1)
(69.1)
Or, nous avons  .
D'où nous déduisons: .
D'où nous déduisons:
 (69.2)
(69.2)
La distance AC est la distance à vol d'oiseau entre le
point de vue (belvédère) et le bateau que nous observons sur l'horizon.
La distance qui nous intéresse cependant ici est BC:
c'est la distance que nous devrions parcourir à l'altitude 0 pour
rejoindre l'autre bateau.
Dans la suite, nous poserons  . .
Lorsque l'angle  varie
de 0° à 360° (tour complet), nous décrivons toute la circonférence
de la Terre, c'est-à-dire varie
de 0° à 360° (tour complet), nous décrivons toute la circonférence
de la Terre, c'est-à-dire  puisque
la Terre est supposée être ronde. puisque
la Terre est supposée être ronde.
Utilisation de la règle de trois:
Si un angle de 360° correspond à une distance de longueur  alors
un angle de alors
un angle de  correspond à une
distance: correspond à une
distance:
 (69.3)
(69.3)
Or, nous avons vu précédemment que:
 (69.4)
(69.4)
D'où, finalement:
 (69.5)
(69.5)
Avec  ,
nous trouvons (h doit être exprimé en kilomètres): ,
nous trouvons (h doit être exprimé en kilomètres):
 (69.6)
(69.6)
Nous avons alors dans le vide, dans un paysage sans obstacles...
la table suivante:
|
Altitude h [m] |
Distance de l'horizon d [km] |
|
5 |
8 |
|
10 |
11.3 |
|
50 |
25.3 |
|
100 |
35.7 |
|
200 |
50.5 |
|
400 |
71.4 |
|
600 |
87.5 |
|
800 |
101 |
|
1000 |
113 |
|
2000 |
159.7 |
|
3000 |
195.6 |
|
4000 |
225.8 |
|
5000 |
252.5 |
|
10000 |
357 |
Tableau: 69.1
- Horizon visuel en fonction de l'altitude
Remarque: Si
nous ne tenons donc pas compte de la réfraction
atmosphérique, nous constatons qu'il faudrait une altitude de l'ordre
de plusieurs kilomètres pour voir au-delà de 200 [km] de distance.
Pourtant, sans aller très loin, depuis les hauteurs de Nice (Alpes-Maritimes),
il est possible d'observer la pointe du Cap Corse qui se trouve à environ
220 km du continent!!! La réfraction atmosphérique joue donc
un rôle dans ce phénomène.
DIRECTION DES VENTS
Nous allons démontrer mathématiquement maintenant
quelque chose de tout à fait intuitif: que les vents se déplacent
des hautes vers les basses pressions (c'est bête comme ça mais
il faut tout de même le montrer).
Nous savons (cf. chapitre de Mécanique
Des Milieux Continus) que la force de pression s'exerçant
sur une surface S est normale à cette surface et vaut
sous forme scalaire  . .
Pour une parcelle d'air de volume  la
force de pression totale selon la direction x vaut alors: la
force de pression totale selon la direction x vaut alors:
 (69.7)
(69.7)

De plus, nous avons (cf. chapitre de Calcul
Différentiel Et Intégral):
 (69.8)
(69.8)
Donc:
 (69.9)
(69.9)
La force de pression massique est donc:
 (69.10)
(69.10)
Nous pouvons faire le même calcul selon y. Finalement,
la force de pression horizontale massique sera donnée par:
 (69.11)
(69.11)
Ainsi, la force de pression (massique ou non) est opposée au
gradient horizontal. La transmission de l'information (de la force)
se fait à la vitesse du son pour cette équation (ce
qui explique la vitesse des appels d'air dans votre maison ou appartement
et la force pouvant faire claquer les portes ou fenêtre).
Elle est donc:
- Dirigée des hautes vers les basses pressions, perpendiculaire
aux isobares
- Inversement proportionnelle à l'écartement des
isobares.
Si nous relevons les valeurs de la pression atmosphérique
en différents
points du globe et que nous relions entre eux les points
de pression identique, nous obtenons une série de courbes,
appelées
"isobares". Le vent est
directement déterminé par ce relief atmosphérique,
puisque c'est un déplacement
d'air entre des hautes vers les basses pressions.
La vitesse du vent est donc fixée par le gradient de pression: autrement dit, si la pression atmosphérique varie rapidement avec
la distance, le vent soufflera fort, tandis qu'il sera faible dans
un "marais" barométrique où cette pression reste quasiment
inchangée sur de grandes distances. En résumé, plus les isobares
sont rapprochées, plus le vent soufflera fort.
Les isobares sont traditionnellement indiquées par un
pas de 5 millibars sur les cartes météo tel que
le montre l'exemple ci-dessous:

Figure: 69.2 - Représentation typique des isobares (sur une dépression)
Ensuite, les météorologues ont défini empiriquement (c'est sympathique
pour la culture générale) une unité de mesure des vents qui n'est
qu'une correspondance entre la force du vent et la distance séparant
2 isobares (5 en 5 [mb]):
|
Distance
entre isobares [km] |
Unité
[Beaufort] |
Vitesse
[m/s] |
600
(brise légère) |
2 |
1.6-3.3 |
500
(brise moyenne) |
4 |
3.4-5.4 |
400
(brise fraîche) |
5 |
8-10.7 |
300
(vent fort) |
6 |
10.8-13.8 |
200
(grand vent) |
7 |
13.9-17.1 |
100
(tempête) |
9 |
20.8-24.4 |
Tableau: 69.2
- Distance entre isobares et vents
MODÈLE ATMOSPHÉRIQUE EXPONENTIEL
Considérons que l'atmosphère est un fluide parfait
dans un champ de gravité. Alors à partir de la relation
du théorème de Bernoulli
suivante, démontrée dans le chapitre de Mécanique
Des Milieux Continus (fluide statique):
 (69.12)
(69.12)
Il vient alors:
 (69.13)
(69.13)
Ainsi, pour connaître la variation de pression avec l'altitude
dans l'atmosphère ou la profondeur dans l'océan,
nous avons pris comme hypothèse "l'équilibre
hydrostatique",
soit que la variation de pression avec la hauteur/profondeur est
proportionnelle à la gravité et à la densité du
fluide.
Ceci n'est bien évidemment pas valide dans le cas de
mouvements rapides de convection, comme dans les orages, mais se
vérifie assez
bien dans les mouvements plus lents et à grande échelle:
l'échelle
synoptique.
Nous allons alors combiner cette dernière relation avec
une équation
d'état, par exemple celle du gaz parfait à la température T
et de densité  dont
les particules constituantes ont pour masse m. Nous avons
donc l'équation des gaz parfaits (cf.
chapitre de Mécanique Des Milieux Continus): dont
les particules constituantes ont pour masse m. Nous avons
donc l'équation des gaz parfaits (cf.
chapitre de Mécanique Des Milieux Continus):
 (69.14)
(69.14)
avec pour rappel P est la pression exprimée en
Pascals, V le
volume exprimé en mètres cubes, R qui est
la constante des gaz parfaits, T la température
exprimée
en Kelvins, n le nombre de moles, k est la constante
de Boltzmann,  la
densité de particules, m la masse totale des particules. la
densité de particules, m la masse totale des particules.
Dans le cas isotherme (par exemple dans la stratosphère
Terrestre, au-dessus de 10 [km] d'altitude où la température
est quasi constante autour de -55 degrés Celsius), l'intégration
s'effectue facilement:
 (69.15)
(69.15)
Donc, à une pression donnée, le gradient vertical de pression
est inversement proportionnel à la température.
Considérons maintenant la relation suivante:
 (69.16)
(69.16)
En utilisant l'exponentielle:
 (69.17)
(69.17)
La pression décroit donc exponentiellement avec l'altitude.  étant
la pression au niveau du sol. étant
la pression au niveau du sol.
Revenons aussi à la relation:
 (69.18)
(69.18)
Elle peut bien évidemment aussi s'écrire sous la forme:
 (69.19)
(69.19)
qui nous dit que la distance z entre les surfaces isobares est
directement proportionnelle à la température.
Voyons également une autre approche courante. Repartons pour
cela de la relation démontrée plus haut mais pour une masse m de
1 kilo:
 (69.20)
(69.20)
et notons cette relation sous la forme suivante:
 (69.21)
(69.21)
Rappelons que (cf. chapitre de Calcul Différentiel
Et Intégral):
 (69.22)
(69.22)
Donc:
 (69.23)
(69.23)
et supposons maintenant que la variation de température
est linéaire
dans l'atmosphère (ce qui n'est pas loin de la vérité pour
les 10 à 20
premiers kilomètres de l'atmosphère) tel que:
 (69.24)
(69.24)
avec  qui
est le gradient de température en [°K/m]. qui
est le gradient de température en [°K/m].

Figure: 69.3 - Profil type de la température et de la pression sur Terre (fin 20ème
siècle)
Nous avons alors:
 (69.25)
(69.25)
Soit:
 (69.26)
(69.26)
Ce qui donne:
 (69.27)
(69.27)
Après simplification:
 (69.28)
(69.28)
Soit:
 (69.29)
(69.29)
Soit écrit de manière plus esthétique:  (69.30)
(69.30)
Un bon exemple d'application courant de cette relation est les
planeurs et les deltaplanes. Ceux-ci attendent de la météo
que celle-ci leur communique l'altitude de l'isotherme du zéro
degré lors de ses bulletins. Ils en déduisent alors
le gradient de température par mètre. Pour ces sportifs,
une bonne condition est d'avoir un gradient de 1 [°C] pour
100 mètres. Il est dès lors
aisé avec la relation précédente de calculer
la pression à une altitude de 2'000 mètres et d'en
déduire
le gradient de pression qui leur permet d'utiliser certains ascendants
pour leurs exercices de voltige.
MODÈLE ATMOSPHÉRIQUE
ADIABATIQUE
Le gradient thermique adiabatique est, dans l'atmosphère terrestre,
la variation de température de l'air avec l'altitude (autrement
dit le gradient de la température de l'air), qui ne dépend que
de la pression atmosphérique, c'est-à-dire: - Sans considération d'échange de chaleur avec l'environnement
(autres masses d'air, relief) - Sans considération de condensation (formation de nuages)
ni de précipitation. Ce concept a une grande importance en météorologie, ainsi qu'en
navigation aérienne et maritime.
Nous avons démontré dans le chapitre de Thermodynamique
la loi de Laplace (satisfaite que sous certaines conditions!):
 (69.31) (69.31)
avec le coefficient de Laplace:
 (69.32)
(69.32)
Soit sous forme massique:
 (69.33)
(69.33)
Nous pouvons en prendre le logarithme:  (69.34)
(69.34)
Or en prenant la différentielle logarithmique:  (69.35)
(69.35)
Nous avons alors (relation que nous retrouverons dans le chapitre
de Musique Mathématiques):
 (69.36)
(69.36)
Nous aurions aussi pu trouver ce résultat directement à partir
de la relation démontrée dans le chapitre de Thermodynamique:
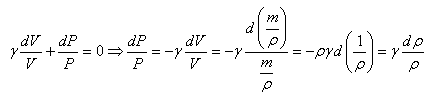 (69.37)
(69.37)
En prenant aussi la différentielle logarithmique de
loi des gaz parfaits où n est le nombre de moles:
 (69.38)
(69.38)
Mais sous la forme massique pour une mole:  (69.39)
(69.39)
où  est
donc la masse molaire, nous avons: est
donc la masse molaire, nous avons:
 (69.40)
(69.40)
Soit:  (69.41)
(69.41)
Nous obtenons alors:  (69.42)
(69.42)
Soit:  (69.43)
(69.43)
Utilisons la relation démontrée plus haut:  (69.44)
(69.44)
Il vient alors:  (69.45)
(69.45)
Nous avons donc une atmosphère à gradient thermique
constant et négatif (la température diminue de
manière linéaire avec l'altitude):
 (69.46)
(69.46)
La dernière forme utilisant la masse molaire étant
plus pratique car elle permet de caractériser le milieu étudié.
À remarquer que c'est un modèle qui semble très
très bien marcher
pour une altitude de 0 à 90 [km] sur la planète
Vénus mais nettement moins bien pour la planète
Terre.
Nous avons alors par exemple pour la Terre (donc tout en sachant
que le modèle n'est pas très bien adapté)  , ,  et
le coefficient adiabatique pour l'air et
le coefficient adiabatique pour l'air  ,
et sa masse molaire ,
et sa masse molaire 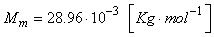 . .
Soit:  (69.47)
(69.47)
ce qui correspond à l'idée courante (un degré pour
100 mètres). ÉQUATION HYPSOMÉTRIQUE
Nous avons donc pour l'équilibre hydrostatique:
 (69.48)
(69.48)
où n est le nombre de moles par kilogramme.
Nous pouvons intégrer cette relation si nous connaissons T
en fonction de P ou z. La mesure directe de P
dans la pratique est plus facile (les altimètres simples sont en
fait des baromètres).
Nous pouvons alors séparer les variables:
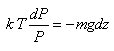 (69.49)
(69.49)
En intégrant entre deux niveaux a et b:
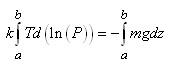 (69.50)
(69.50)
Puisque:
 (69.51)
(69.51)
Ensuite pour continuer nous allons utiliser une astuce. Nous allons
définir la température moyenne par la relation:
 (69.52)
(69.52)
Ce qui nous permet alors d'écrire:
 (69.53)
(69.53)
Soit:
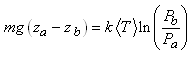 (69.54)
(69.54)
où autrement écrit:
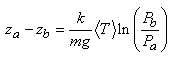 (69.55)
(69.55)
Les deux relations encadrées sont appelées chacune
respectivement "équation
hypsométrique" (du grec "hypso" pour "hauteur"):
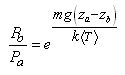 (69.56)
(69.56)
Remarque: En
météorologie,  est
posé comme étant égal à 0 au niveau de la
mer où la pression  est
supposée connue. Ainsi, nous avons trois paramètres
libres. En en connaissant deux sur les trois, il est facile de
déterminer
le troisième.
À l'armée, par exemple, les ballons-sondes
donnent la température
et la hauteur du ballon et les militaires au sol mesurent  et et
 .
Ensuite toutes ces informations sont communiquées aux chars
d'assaut qui peuvent calculer la pression .
Ensuite toutes ces informations sont communiquées aux chars
d'assaut qui peuvent calculer la pression  à
différentes hauteurs et donc l'influence de celle-ci sur
la trajectoire de leurs obus... via la différence de force. à
différentes hauteurs et donc l'influence de celle-ci sur
la trajectoire de leurs obus... via la différence de force.
BALLON-SONDE
Un joli
petit exemple intéressant d'application des mathématiques appliquées
au génie météo est l'étude des fameux ballons-sondes et particulièrement
la caractéristique de leur volume en fonction de l'altitude qui
est souvent sujet à débat dans des groupes de discussion lorsque
personne n'y formalise le problème une bonne fois pour toute. Vous
aurez donc compris que c'est ce que nous allons étudier ici et
surtout nous allons tenter de déterminer le diamètre théorique
de ceux-ci à une altitude donnée.
L'énoncé du
problème souvent débattu est le suivant:
Un ballon-sonde
en PVC (Polyvinyl-Chloride) de masse m sert à emmener à haute
altitude un appareillage en vue d'effectuer des mesures. L'enveloppe
du ballon contient n moles de gaz parfait d'hydrogène 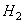 ayant
donc une masse molaire de: ayant
donc une masse molaire de:
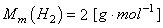 (69.57)
(69.57)
L'atmosphère
sera assimilée à un gaz parfait, de masse molaire moyenne:
 (69.58)
(69.58)
aux C.N.T.P.
(Conditions Normales de Température et de Pression).
Nous
voulons d'abord chercher quelle est la force ascensionnelle 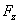 ressentie
par le ballon? ressentie
par le ballon?
Ensuite,
nous voulons évaluer la quantité de matière minimale 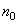 assurant
le décollage de celui-ci pour une masse totale (ballon compris!)
de 2.6 [Kg]. puis le volume assurant
le décollage de celui-ci pour une masse totale (ballon compris!)
de 2.6 [Kg]. puis le volume 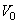 correspondant, à l'altitude
de départ. correspondant, à l'altitude
de départ.
Rappelons
deux choses pour résoudre déjà ce premier point:
1. Tout
corps plongé dans un liquide (ou un gaz) subit une force vers le
haut égale au poids du volume qu'il déplace (force d'Archimède)
selon la relation démontrée dans le chapitre de Mécanique des milieux
continus:
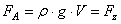 (69.59)
(69.59)
2. Tout gaz parfait ayant une masse en grammes égale à la
masse molaire occupe selon la loi des gaz parfaits un volume de
22.4
[L] à 273.15 [K] et à une pression
de 1 [atm]
comme nous l'avons démontré dans le chapitre de Chimie
Thermique. Ce qui donne aux C.N.T.P:
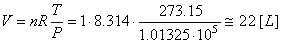 (69.60)
(69.60)
Donc
pour que le ballon flotte à hauteur constante (sans monter
mais sans tomber aussi...) avec juste la quantité 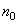 d'hydrogène
suffisante, il faut donc d'après le principe d'Archimède
que le volume d'air qu'il déplace ait un poids égal à la
masse totale du ballon et de la sonde, soit 2.6 [Kg] dans
notre cas! d'hydrogène
suffisante, il faut donc d'après le principe d'Archimède
que le volume d'air qu'il déplace ait un poids égal à la
masse totale du ballon et de la sonde, soit 2.6 [Kg] dans
notre cas!
Donc
puisque 22 [L] d'air pèsent environ 29 grammes, il
faut que le volume soit tel qu'il déplace 2.6 [Kg]
d'air. Soit en faisant une simple règle de trois:
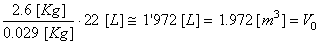 (69.61)
(69.61)
Donc si le ballon est sphérique, cela donne un rayon de:
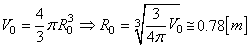 (69.62)
(69.62)
Soit un diamètre d'environ 1.56 [m] au sol. Ce qui
est conforme à la
réalité!
Il nous faut encore déterminer le nombre de moles d'hydrogène.
Il vient immédiatement:
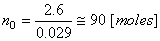 (69.63)
(69.63)
Maintenant
que nous connaissons le nombre de moles dans le ballon, si nous
connaissons la température et la pression à une hauteur de 22'000
[m] (altitude type d'un petit ballon-sonde) il ne nous
reste qu'à appliquer la loi des gaz parfaits pour connaître le
volume à cette
altitude donné alors par la relation démontrée dans le chapitre
de Mécanique des Milieux Continus:
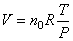 (69.64)
(69.64)
ainsi à 22'000 [m] d'altitude, nous avons environ
selon les tables disponibles sur Internet:
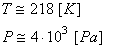 (69.65)
(69.65)
Mais au fait le rayonnement solaire est environ 30% plus élevé à cette
altitude et le ballon est considéré comme un système adiabatique
(sans échange de chaleur) et ne restitue donc pas la puissance
emmagasinée à l'environnement extérieur. Nous considérons alors
que la température est au moins 30% plus élevée ce qui nous donne
comme chiffres:
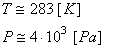 (69.66)
(69.66)
Nous avons donc:
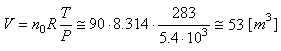 (69.67)
(69.67)
Nous aurions pu également utiliser (hypothèse adiabatique
oblige!) la relation de Boyle-Mariotte (cf.
chapitre de Mécanique Des Milieux
Continus) pour arriver au même résultat:
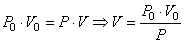 (69.68)
(69.68)
Ce qui donne un rayon d'environ 2.33 [m] (diamètre
donc d'environ 4.6 [m]) au lieu des 0.78 [m] au
sol! Soit une augmentation du diamètre d'environ 300%. Il
est plus important cependant de s'intéresser à l'augmentation
de la surface pour déterminer les forces de contraintes élastiques
sur le PVC. Nous avons donc avant:
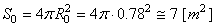 (69.69)
(69.69)
et après:
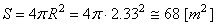 (69.70)
(69.70)
Soit une augmentation de la surface d'environ 1'000% alors qu'un élastomère-type
(dont le PVC fait partie) ne résiste pas à une variation
relative de 500%!!! Il est donc beaucoup plus aisé de comprendre
sous le point de vue de la surface, pourquoi le ballon ne résiste
pas à une
augmentation du diamètre d'environ 300%.
Par ailleurs si nous appliquons de manière un peu abusive la
loi de Hook au ballon (cf. chapitre de Mécanique
des Milieux Continus),
avec le module de Young du PVC qui est compris entre (source
Wikipédia):
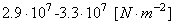 (69.71)
(69.71)
nous
avons:
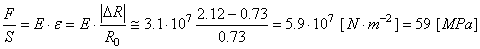 (69.72)
(69.72)
Ce qui est conforme aux données des tables numériques qui donnent
une valeur limite inférieure élastique de 50 [MPa]
et une limite supérieure de 80 [MPa] pour le PVC
(source Wikipédia). Il nous est alors possible de calculer
la hauteur
minimale et maximale
théorique que le ballon peut atteindre.
Ainsi pour la hauteur minimale, nous écrivons d'abord:
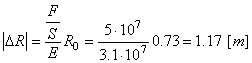 (69.73)
(69.73)
Ce qui correspond alors à un rayon final de:
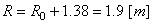 (69.74)
(69.74)
Ce qui correspond à un volume de:
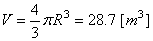 (69.75)
(69.75)
En appliquant Boyle-Mariotte:
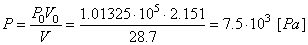 (69.76)
(69.76)
qui est une pression correspondante à une hauteur d'environ
18'000 [m] selon les mesures expérimentales (www.engineeringtoolbox.com)
et c'est effectivement une hauteur à laquelle certains rares
ballons en PVC éclatent.
Maintenant faisons de même avec la hauteur maximale:
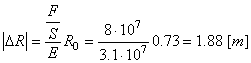 (69.77)
(69.77)
Ce qui correspond alors à un rayon final de:
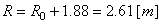 (69.78)
(69.78)
Ce qui correspond à un volume de:
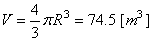 (69.79)
(69.79)
En appliquant Boyle-Mariotte:
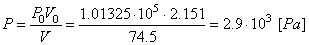 (69.80)
(69.80)
qui est une pression correspondant à une hauteur d'environ 24'000
[m] selon les mesures expérimentales et c'est effectivement
une hauteur à laquelle les ballons en PVC les plus hauts éclatent.
CYCLOGENÈSE ET ANTICYCLOGENÈSE
L'essentiel de la masse atmosphérique est contenu dans les 20
premiers kilomètres d'altitude, si bien que la météorologie à grande
échelle se déroule sur une mince coquille sphérique (assimilable
à de la mécanique des fluides bidimensionnelle).
Le moteur de la circulation atmosphérique dans les tropiques
est le réchauffement solaire. À cause de l'inclinaison
de 23.5 degrés
de l'axe de rotation de la Terre, le Soleil n'est jamais plus qu'à
quelques dixièmes de degré du zénith à midi
tout au long de l'année
dans les tropiques, ce qui donne un maximum de réchauffement
autour de l'équateur géographique.
Il faut donc distinguer la circulation au voisinage des tropiques,
caractérisée par de forts mouvements verticaux, dus aux convections
thermiques, et la circulation des latitudes moyennes, faites quasiment
que de mouvements horizontaux:

Figure: 69.4 - Schéma simplifié de la circulation des vents sur Terre
Supposons un moment que nous arrêtions complètement le mouvement
de l'air dans l'atmosphère relativement à la surface de la planète,
et que nous le laissions ensuite recommencer à tourner d'Ouest en
Est (de gauche à droite sur les images) partir du repos. La force
du gradient de pression pousse l'air à se mouvoir des régions de
haute pression vers les régions de basse pression (appel du vide).
Ces mouvements de convections sont appelés des "cellules
de Hadley".
Toutefois, dès que le mouvement s'amorce la force de Coriolis
(due à la rotation de la Terre) dévie donc les vents Nord-Sud
en direction de l'Ouest et les vents Sud-Nord vers l'Est pour
un observateur
se situant au pôle Nord. Nous observons dès lors la formation
de cyclones tournants dans le sens contraire des aiguilles d'une
montre
dans l'hémisphère Nord et inversement dans l'hémisphère
Sud (à cause
de la direction du vecteur  dans
cette partie de l'hémisphère). dans
cette partie de l'hémisphère).
Plus la vitesse de l'air augmente, plus la force de Coriolis
augmente de concert en accentuant la déviation. Éventuellement
la force de Coriolis atteint une valeur égale et opposée à celle
de la force du gradient de pression, produisant ainsi un écoulement
d'une vitesse constante (sans accélération), parallèle aux isobares
définissant
ainsi la limite géométrique de la cellule de Hadley. C'est ce que
nous appelons"l'équilibre géostrophique".
En pratique, l'écoulement en dehors des tropiques est presque
toujours en quasi-équilibre géostrophique.
En l'absence d'observations de vent, les météorologues
peuvent estimer la force du vent en un point donné en mesurant
sur une carte d'analyse météo le gradient de pression
et la latitude. L'approximation géostrophique est purement
diagnostique. Elle n'a pas de valeur prédictive, car son équation
ne contient aucun terme de changement.
Dans les tropiques, où la force de Coriolis est de plus en plus
faible jusqu'à être nulle à l'équateur, ce sont d'autres forces,
comme la force centrifuge, qui viennent équilibrer la force de gradient
de pression.
C'est ce que nous allons démontrer ici mathématiquement à l'aide
de la mécanique des milieux continus (fluides) et la mécanique
classique (voir chapitres correspondants).
Nous savons que dans notre système intervient donc les forces
de pression (gradient), les forces centrifuges, les forces de
pesanteur
(gravité). Forces auxquelles il ne faut pas oublier d'ajouter la
force (implicitement: l'accélération) de Coriolis interne au
système
(sous-entendu le cyclone) de pulsation  (cf.
chapitre de Mécanique Classique): (cf.
chapitre de Mécanique Classique):
 (69.81)
(69.81)
et la force (implicitement: l'accélération) de Coriolis par unité
de masse de fluide (la raison de ce choix d'unité paraîtra évidente
quelques paragraphes plus loin) relativement à la pulsation  de
la Terre: de
la Terre:
 (69.82)
(69.82)
Ainsi, comme nous le savons (cf. chapitre
de Mécanique Classique), la force de Coriolis va tendre à
dévier tout mouvement descendant vers la droite (Est) dans l'hémisphère
Nord et tout mouvement montant vers la gauche (Ouest) dans l'hémisphère
Sud (selon que l'on se place dans la direction du fluide en mouvement
selon la figure précédente).
C'est ainsi que l'air à la base des cellules de Hadley, voyageant
à basse altitude du tropique vers l'équateur sera dévié vers l'Ouest
pour donner les Alizés de vents d'Est.
Nous avons par ailleurs démontré dans le chapitre de mécanique
des milieux continus une forme particulière de l'équation d'Euler
de 2ème forme qui était:
 (69.83)
(69.83)
Remaniée, cette relation s'écrit aussi:
 (69.84)
(69.84)
Or, nous avions aussi démontré que:
 (69.85)
(69.85)
Il vient dans le référentiel Terrestre:
 (69.86)
(69.86)
Il s'agit donc de l'équation définissant la pression à l'intérieur
du fluide considéré comme isolé. À cette
relation, il faut donc encore soustraire les forces de pression
de Coriolis
dues au référentiel
géocentrique pour obtenir la dynamique du système "cyclone":
 (69.87)
(69.87)
Ce qui donne finalement:
 (69.88)
(69.88)
Soit sous forme condensée traditionnelle:
 (69.89)
(69.89)
Représentons maintenant la Terre dans une tranche Nord-Sud:

Figure: 69.5 - Tranche Nord-Sud de la Terre
Si nous agrandissons la repère lié au cyclone et
y translatons le vecteur pulsation de la Terre, nous avons:

Figure: 69.6 - Repère lié au cyclone avec la pulsation plane
Soit:
 (69.90)
(69.90)
Nous avons donc:
 (69.91)
(69.91)
Comme nous étudions les mouvements (quasi) horizontaux dans l'atmosphère
à cette latitude, nous pouvons considérer que les particules de
fluide sont assujetties à demeurer dans le plan horizontal  .
Les composantes de la force de Coriolis pour un mouvement plan sont
alors ( .
Les composantes de la force de Coriolis pour un mouvement plan sont
alors ( ): ):
 (69.92)
(69.92)
où f est appelé "paramètre de
Coriolis". Donc la force de Coriolis en océanographie
et en météorologie est traditionnellement notée:
 (69.93)
(69.93)
Le nombre f, positif dans l'hémisphère Nord,
négatif dans
l'hémisphère Sud, varie de 0 à 1.458 aux pôles alors
que la force est de l'ordre du millième de Newton pour
les masses de fluide (courants océaniques) et du même ordre
de grandeur (car la vitesse compense la faible densité)
pour les gaz (courants atmosphériques).
Nous appliquons maintenant l'approximation de l'équilibre
géostrophique,
c'est-à-dire que nous considérons que l'air est animé d'un
mouvement rectiligne uniforme (vent géostrophique), en
d'autres termes, nous négligeons l'action de la force centrifuge
due à la rotation du
tourbillon devant celle de la force de Coriolis due à la rotation
de la Terre, ce qui revient à supposer que:
 (69.94)
(69.94)
avec R étant le rayon du tourbillon et  sa
pulsation. Puisque (cf. chapitre de Mécanique
Classique): sa
pulsation. Puisque (cf. chapitre de Mécanique
Classique):
 (69.95)
(69.95)
cette dernière inégalité devient:
 (69.96)
(69.96)
où:
 (69.97)
(69.97)
est appelé le "nombre de Rossby"
et n'a pas de dimensions.
Remarque: Pour
les moyennes latitudes (  ),
l'expérience et les mesures donnent  et
 .
La valeur limite pour laquelle  est
 .
Pour une échelle supérieure, comme c'est le cas pour les cyclones
où  ,
nous sommes donc proche de l'équilibre géostrophique. Pour une échelle
inférieure, Coriolis est négligeable et le vent est accéléré des
hautes vers les basses pressions.
Le nombre de Rossby représente donc le rapport entre les forces
d'inerties et les forces dues à la rotation qui caractérisent le
mouvement d'un fluide dans un repère tournant.
Ainsi, nous pouvons faire la différence entre un écoulement géophysique
à fort nombre de Rossby ou à faible nombre de Rossby. Si le nombre
de Rossby est très supérieur à l'unité, alors les forces de Coriolis
dues par exemple à la rotation terrestre sont négligeables devant
l'inertie de l'écoulement. Dans le cas contraire d'un nombre de
Rossby très inférieur à l'unité, les forces de Coriolis dominent
le mouvement du fluide.
Ainsi, si on se rapproche de l'équateur, f tendant
vers 0 le nombre de Rossby devient très grand et aux pôles
il devient respectivement très faible.
Dans le cadre de cette approximation, notre équation d'Euler peut
alors s'écrire sous la forme:
 (69.98)
(69.98)
et puisque nous nous intéressons qu'au plan horizontal de l'atmosphère
cela ce simplifie encore plus sous la forme:
 (69.99)
(69.99)
Soit totalement sous forme vectorielle développée et en reprenant
la majuscule P pour la pression comme il est d'usage en météorologie:
 (69.100)
(69.100)
Il vient ainsi que:
 (69.101)
(69.101)
soit:
 (69.102)
(69.102)
Donc sous forme conventionnelle:
 (69.103)
(69.103)
La norme étant donnée par:
 (69.104)
(69.104)
Soit:
 (69.105)
(69.105)
relation qui est appelée "équation
des vents (géostrophiques)".
Quatre scénarios sont à considérer:
1. Nous sommes dans l'hémisphère Nord et donc f est positif.
Supposons que dP/dR soit positif, la pression augmente
alors en s'éloignant du centre du tourbillon (qui lui est donc un
minimum de basse pression). Dès lors v est positif et nous
avons un tourbillon appelé "dépression" dans l'hémisphère
Nord. Ainsi, le fluide (le vent) souffle autour de la dépression
dans le sens antihoraire (vers l'Ouest) dans l'hémisphère Nord.
Définitions:
D1. Une "dépression" (ou
"basse pression") est une
zone où la pression atmosphérique diminue horizontalement vers un
centre de basse pression, c'est-à-dire un minimum local de pression.
D2. Les systèmes atmosphériques intenses à circulation
autour d'un centre fermé de basse pression (comme un aspirateur
cela attire les nuages d'où le fait que les cyclones sont
visibles sur des photos satellites) reçoivent systématiquement
le terme plus général de "cyclone" ou
de
"cyclone tropical".
Remarque: Nous
associons les dépressions au mauvais temps, car
la dynamique qui entoure une dépression présuppose l'existence
de courants ascendants (peuvent difficilement entrer dans le
sol donc
la seule voie d'échappement est le haut!) qui provoquent des nuages
et de la précipitation. De plus, le gradient de pression autour
d'une dépression peut engendrer de forts vents.
2. Nous sommes toujours dans l'hémisphère Nord et
donc f
est positif. Supposons que dP/dR soit cette fois
négatif,
la pression diminue alors en s'éloignant du centre du tourbillon
(qui lui est donc un maximum de haute pression). Dès lors v
est négatif et nous avons un tourbillon appelé "haute
pression"
dans l'hémisphère Nord. Ainsi, le fluide (le vent)
souffle autour de la haute pression dans le sens horaire (vers
l'Est) dans l'hémisphère
Nord.
Définitions:
D1. Une "haute pression"
est une zone où la pression atmosphérique augmente horizontalement
vers un centre de haute pression, c'est-à-dire un maximum local
de pression.
D2. Les systèmes atmosphériques intenses à circulation
autour d'un centre fermé de haute pression (comme un ventilateur
cela rejette et disperse les nuages d'où le fait que les
anticyclones ne sont pas visibles de manière simple sur
les photos satellites) reçoivent systématiquement le terme
plus général de "anticyclone".
Remarque: Les
anticyclones généralement apportent du beau temps
et des ciels clairs. La dynamique atmosphérique fait en sorte
que l'air aux altitudes moyennes y est relativement chaud et
sec, et
donc sans nuages.
3. Nous sommes toujours dans l'hémisphère Sud et
donc f
est négatif. Supposons que dP/dR soit positif,
la pression augmente alors en s'éloignant du centre du
tourbillon. Dès lors v est négatif et nous
avons un tourbillon appelé
"haute pression" (ou "anticyclone") dans l'hémisphère
Sud. Ainsi, le fluide (le vent) souffle autour de la haute pression
mais dans le sens antihoraire (vers l'Ouest) dans l'hémisphère
Sud.
4. Nous sommes toujours dans l'hémisphère Sud et
donc f
est négatif. Supposons que dP/dR soit négatif,
la pression diminue alors en s'éloignant du centre du tourbillon.
Dès
lors v est positif et nous avons un tourbillon appelé "basse
pression"
(ou "cyclone") dans l'hémisphère Sud. Ainsi,
le fluide (le vent) souffle autour de la basse pression dans le
sens horaire
(vers l'Est) dans l'hémisphère Sud.
Remarque: Il
est donc possible de dire de manière générale
sur les grandes dimensions que le vent arrive des hautes pressions
(Anticyclone) pour se diriger vers les basses pressions (Dépression).
Voici un exemple d'une image de dépression (anticyclone)
et haute pression (cyclone) dans l'hémisphère Nord
tel que le représentent les professionnels
de la météorologie:

Figure: 69.7 - Basse pression et haute pression
Nous pouvons effectivement observer que la dépression (D)
tourne dans le sens antihoraire et la haute pression (A) dans
le sens horaire
(et inversement dans l'hémisphère Sud).
Remarque: L'air
au centre d'un anticyclone (A) descend vers la surface, subissant
une compression et par conséquent un échauffement.
Pour une dépression (D), c'est le phénomène inverse qui se produit.
MARÉES
Parmi les phénomènes de la nature, la marée est l'un des plus
majestueux par son ampleur et par sa puissance, l'un des plus
surprenants
par sa régularité et par la discrétion de ses causes. On comprend
sans peine non seulement qu'il se soit imposé à l'attention des
navigateurs mais encore qu'il ait, depuis la plus lointaine antiquité,
suscité les recherches des savants les plus émérites.
Pour aborder le sujet des marées de manière simple, nous pouvons
partir d'un constat logique: Si l'attraction lunaire était identique
en chaque point de la Terre, il n'y aurait pas de marées. Il
faut donc aborder l'étude des marées sur les différences de
forces. L'influence de la Lune sur la marée est appelée "composante
diurne".
PREMIÈRE APPROCHE
Considérons pour l'étude naïve du
phénomène
une masse d'eau m
à l'équateur et aux pôles. Nous allons calculer
la force d'attraction sur cette masse par rapport au centre de
la Terre et
en prenant en compte l'influence de la Lune de masse  . .

Figure: 69.8 - Configuration Terre-Lune pour l'étude des marées
Commençons par calculer la force 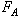 à
l'équateur au point le plus proche de la Lune relativement à la
figure ci-dessus. à
l'équateur au point le plus proche de la Lune relativement à la
figure ci-dessus.
Nous avons alors:
 (69.106)
(69.106)
en considérant que  et
en notant la "force de marée statique": et
en notant la "force de marée statique":
 (69.107)
(69.107)
Une application numérique pour une masse m de 1 [Kg]
donne:
 (69.108)
(69.108)
Sous forme vectorielle nous avons bien évidemment:
 (69.109)
(69.109)
Comme la distance Terre-Lune atteint environ 60 rayons terrestres,
l'intensité de l'accélération varie à peu près linéairement (...)
le long de la portion terrestre d'une droite passant par le centre
de la Lune. C'est notamment le cas pour le segment qui relie les
deux points antipodaux A et C de la figure ci-dessus.
Nous pouvons donc écrire, O désignant le centre
de la Terre:
  (69.110)
(69.110)
Nous devons maintenant séparer les deux contributions de la Lune.
- La force  qui
s'applique sur le centre de masse G est donc uniforme
à la planète par construction. C'est cette force qui est responsable
de la révolution de notre planète autour du centre de masse commun
aux deux astres. qui
s'applique sur le centre de masse G est donc uniforme
à la planète par construction. C'est cette force qui est responsable
de la révolution de notre planète autour du centre de masse commun
aux deux astres.
- Le terme résiduel  se
superpose et prend des valeurs opposées aux antipodes. Elle est
responsable des marées (en première approximation dans ce modèle
simpliste). se
superpose et prend des valeurs opposées aux antipodes. Elle est
responsable des marées (en première approximation dans ce modèle
simpliste).
Ainsi, la force due à la Lune est de signe opposé sur
l'horizontale. Nous avons alors deux marées (lunaires)
par jour à des lieux antipodaux:
- Celle de la Lune qui attire (de ce côté-ci de la Terre)
- Celle de la Lune qui repousse (du côté opposé de la Terre)
Soit sous forme schématique (sans aucun respect des proportions
réelles):

Figure: 69.9 - Lieux antipodaux des marées
Si l'on considérait la surface de la Terre comme parfaitement
sphérique et recouverte d'eau, elle prendrait alors la forme d'une
ellipsoïde dont l'axe serait dirigé vers l'astre générant la
marée.
Nous observerions alors des marées dont les pleines et basses mers
auraient lieu deux fois par jour et toujours à la même heure.
Nous appelons cette situation la "marée
statique"
et le modèle correspondant "modèle statique
des marées".
Il convient de préciser que le jeu subtil entre la rotation de
la Terre et la Lune produit des frottements gigantesques au niveau
des masses d'eau qui ont pour effet de ralentir la vitesse de rotation
de la Terre d'environ 1 seconde tous les mille ans.
DEUXIÈME APPROCHE
Pour la
deuxième approche, qui vaut la peine d'être vue pour la culture générale et aussi
parce qu'elle présente un autre aspect intéressant de l'explication de l'attraction
entre deux astres, considérons le schéma suivant:

Figure: 69.10 - Approche schématique de l'approche
Nous avons démontré dans le chapitre de Trigonométrie le théorème
du cosinus (formule d'Al-Kashi) qui nous donne:
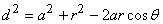 (69.111)
(69.111)
d'où le potentiel gravitationnel (cf. chapitre
d'Astronomie):
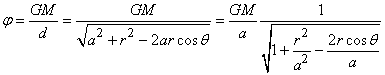 (69.112)
(69.112)
Mais:
 (69.113)
(69.113)
et le potentiel gravitationnel est de la forme:
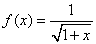 (69.114)
(69.114)
que nous pouvons développer en série de Maclaurin (cf.
chapitre Suites Et Séries) jusqu'à l'ordre 2:
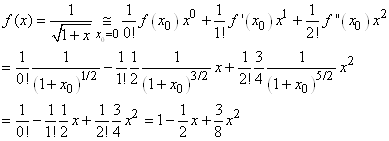 (69.115)
(69.115)
Le potentiel gravitationnel devient alors:
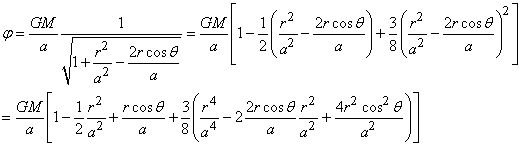 (69.116)
(69.116)
Si nous ne gardons que les termes de puissance 1 et 2 en r/a,
il reste:
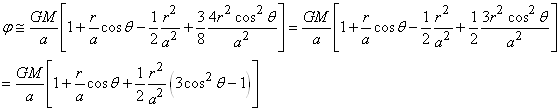 (69.117)
(69.117)
Le premier terme du potentiel est :
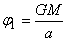 (69.118)
(69.118)
C'est le potentiel pour 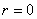 ,
c'est-à-dire le potentiel crée par la Lune au centre de la Terre. ,
c'est-à-dire le potentiel crée par la Lune au centre de la Terre.
Ce terme ne contient aucune variable, il est constant et donc son gradient
est nul, il ne donne lieu à aucune force puisque:
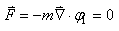 (69.119)
(69.119)
Le deuxième terme:
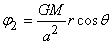 (69.120)
(69.120)
contient les deux variables r et 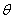 .
Son gradient ne sera pas nul. Il va générer une force de gravitation
que nous allons calculer, mais en utilisant une astuce. .
Son gradient ne sera pas nul. Il va générer une force de gravitation
que nous allons calculer, mais en utilisant une astuce.
Puisque:
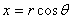 (69.121)
(69.121)
Il vient:
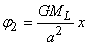 (69.122)
(69.122)
Dès lors, le gradient en coordonnées cartésiennes se réduit pour
la masse dm se situant au point A à:
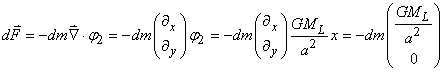 (69.123)
(69.123)
Donc tous les éléments de la Terre subissent de la part de la
Lune des forces parallèles (selon l'axe X seulement) dirigées
vers la Lune. La masse totale de la Terre est la somme de toutes
ces masses et la force totale que subit la Terre de la part de
la Lune est la somme des forces élémentaires. Donc:
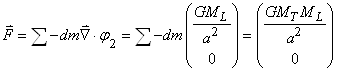 (69.124)
(69.124)
et donc la force totale est seulement selon l'axe X et
est donnée par:
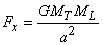 (69.125)
(69.125)
Cette force est la même que si toute la masse de la Terre était
concentrée au centre T
et si toute la masse de la Lune était concentrée au centre L.
La Lune subit de la part de la Terre la même force de sens contraire,
c'est le principe des actions mutuelles. C'est cette dernière qui
oblige la Lune à tourner autour de la Terre.
Le troisième terme est celui responsable des marées:
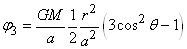 (69.126)
(69.126)
La force dérivant du gradient en coordonnées polaires étant donnée
par:
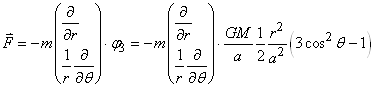 (69.127)
(69.127)
Donc, la composante radiale de la force est:
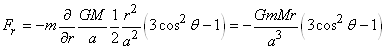 (69.128)
(69.128)
la composante orthoradiale:
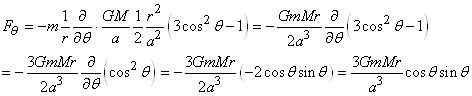 (69.129)
(69.129)
Donc:
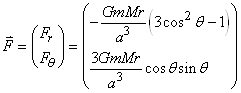 (69.130)
(69.130)
Pour une masse m d'eau, la force de marée est:
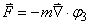 (69.131)
(69.131)
Pour 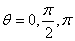 ,
la composante orthoradiale ,
la composante orthoradiale 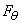 s'annule.
Nous avons alors pour ces trois angles: s'annule.
Nous avons alors pour ces trois angles:
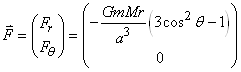 (69.132)
(69.132)
Pour 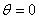 la
force est uniquement radiale: la
force est uniquement radiale:
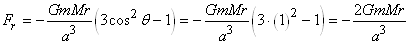 (69.133)
(69.133)
Le signe de cette force est positif et il est dirigé vers la Lune.
Pour 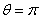 la
force est aussi uniquement radiale et on retombe sur la même expression: la
force est aussi uniquement radiale et on retombe sur la même expression:
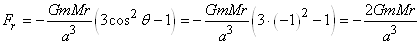 (69.134)
(69.134)
Donc, l'amplitude est la même pour l'angle 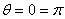 . .
Par contre, si le lecteur se rappelle que pour revenir en composantes
cartésiennes nous avons:
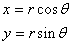 (69.135)
(69.135)
Nous voyons alors que pour 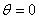 ,
la force est orientée dans le sens positif de l'axe X puisque x sera
positif (mais nulle selon Y). Il y a donc une marée dans
la direction de la Lune (intuitif) ,
la force est orientée dans le sens positif de l'axe X puisque x sera
positif (mais nulle selon Y). Il y a donc une marée dans
la direction de la Lune (intuitif)
Nous voyons aussi que pour 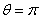 ,
la force est orientée dans le sens négatif de l'axe X puisque x sera
négatif (mais nulle selon Y). Il y a donc une marée dans
la direction opposée à la Lune (contre intuitif). ,
la force est orientée dans le sens négatif de l'axe X puisque x sera
négatif (mais nulle selon Y). Il y a donc une marée dans
la direction opposée à la Lune (contre intuitif).
Pour 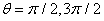 ,
la composante x est nulle et la composante radiale sera: ,
la composante x est nulle et la composante radiale sera:
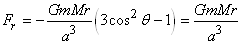 (69.136)
(69.136)
et elle est dirigée vers le centre de la Terre puisque:
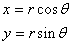 (69.137)
(69.137)
Nous voyons alors que pour 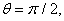 la
force est orientée dans le sens positif de l'axe Y puisque y sera
positif (mais nulle selon X). Nous voyons aussi que pour la
force est orientée dans le sens positif de l'axe Y puisque y sera
positif (mais nulle selon X). Nous voyons aussi que pour 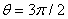 ,
la force est orientée dans le sens négatif de l'axe Y puisque y sera
négatif (mais nulle selon x). ,
la force est orientée dans le sens négatif de l'axe Y puisque y sera
négatif (mais nulle selon x).
En réalité, les marées sont beaucoup plus
complexes que le modèle ci-dessus (excentricité de l'orbite
lunaire, superposition de la marée diurne, orbite lunaire, alignement
Lune-Soleil, inclinaison du plan de l'orbite de la Lune, équinoxes,
etc.). Voici une superbe animation de l'élévation
de la surface des océans
en mètre, sur 1 cycle de marée, calculée à
partir d'un modèle plus élaboré:

Figure: 69.11 - Complexité réelle des marées sur Terre (source:
Wikipédia)
Remarque: Le
phénomène est donc dû à la déformation de la surface
des océans par suite des attractions combinées des corps célestes.
Ce mouvement peut même détruire l'astre qui le subit: si la
force de marée l'emporte sur la force de gravitation de ses
constituants, l'astre se désagrège. Cette limite où les forces
de marées l'emportent
sur la force gravitationnelle s'appelle "limite de Roche"
(cf. chapitre d'Astronomie).
Outre la marée diurne due à l'attraction de la Lune, il faut
compter en plus sur une marée due à la force centrifuge du mouvement
de la Terre et de la Lune autour de leur centre de masse (mais
cela dépend des latitudes, du relief et de plein d'autres paramètres
objectivement car sur certains endroits de la planète il n'y a
qu'une seule marée par jour). Effectivement, la Terre et la Lune
tournent autour du centre de masse qui définit l'orbite de couple
Terre-Lune (les échelles ne sont pas respectées):

Figure: 69.12 - Principe des marées superposées aux marées diurne
et nous ferons l'impasse sur les marées d'équinoxes et autres...
jusqu'à ce jour...
ÉQUATION DE LORENZ
La "convection libre" ou "convection
naturelle" est
le régime d'écoulement obtenu lorsque nous chauffons
un fluide sans qu'il n'y ait d'écoulement extérieur
imposé. C'est le cas
des mouvements de convections de l'atmosphère (gaz chauds
dans gaz froids), des mouvements de convections de la roche en
fusion
responsable de la tectonique des plaques, des mouvements de l'eau
chaude sous pression dans les geysers et de bien d'autres phénomènes...
Ces écoulements sont inexplicables si nous ne couplons pas les équations
de la dynamique et de la thermodynamique!
Nous allons dans ce contexte établir le fameux système des équations
de Lorenz au prix cependant de nombreuses approximations et hypothèses
afin de simplifier au maximum les calculs et les outils mathématiques
utilisés (car à l'époque du développement du modèle les ordinateurs
n'étaient pas ce qu'ils sont aujourd'hui).
Nous montrerons ainsi dans le cadre de la convection (une des
dynamiques importante de notre atmosphère) que les équations
qui déterminent certains paramètres du mouvement
sont très sensibles
aux conditions initiales ce qui a pour but de montrer la difficulté de
la prévision à plus ou moins long terme avec des modèles
théoriques
déterministes (raison pour laquelle en météorologie
il est fait usage de nos jours de la méthode des éléments
finis).
A priori, la densité  est
fonction de la température et de la pression par la loi
d'état
des gaz parfaits (cf. chapitre de Mécanique
Des Milieux Continus). Il est
donc naturel de penser que si nous chauffons une paroi, la température
du fluide environnant augmente par diffusion. La stratification
de pression s'en trouve changée, le gradient de pression
crée le
mouvement. est
fonction de la température et de la pression par la loi
d'état
des gaz parfaits (cf. chapitre de Mécanique
Des Milieux Continus). Il est
donc naturel de penser que si nous chauffons une paroi, la température
du fluide environnant augmente par diffusion. La stratification
de pression s'en trouve changée, le gradient de pression
crée le
mouvement.
Dans tous les chapitres du site, nous avons jusqu'à présent négligé toute
variation de  .
Mais le découplage n'est plus valable ici puisque c'est le chauffage
qui provoque le mouvement. Nous allons donc permettre une variation
de la densité avec le chauffage en supposant cependant que cette
perturbation est petite. Il faut donc réintroduire une variation
de .
Mais le découplage n'est plus valable ici puisque c'est le chauffage
qui provoque le mouvement. Nous allons donc permettre une variation
de la densité avec le chauffage en supposant cependant que cette
perturbation est petite. Il faut donc réintroduire une variation
de  autour
d'une position d'équilibre: le repos. En revanche la viscosité sera
supposée constante. autour
d'une position d'équilibre: le repos. En revanche la viscosité sera
supposée constante.
Soit donc un fluide au repos et à la température  au
loin, il est en présence d'une paroi chauffée à la température au
loin, il est en présence d'une paroi chauffée à la température .
Pour obtenir la dépendance de .
Pour obtenir la dépendance de  ,
rappelons les coefficients thermo-élastiques classiques (cf.
chapitre de Thermodynamique): ,
rappelons les coefficients thermo-élastiques classiques (cf.
chapitre de Thermodynamique):
- Coefficient de compressibilité (ou de dilatation suivant l'écriture
en termes de densité) isobare:
 (69.138)
(69.138)
- Coefficient de compressibilité isotherme:
 (69.139)
(69.139)
En admettant maintenant que la densité est principalement reliée à la
température (pour faire simple) nous pouvons écrire (cette hypothèse
marche bien pour les fluides mais pas trop... pour les gaz!!):
 (69.140)
(69.140)
En utilisant la forme générale du développement de Taylor (cf.
chapitre de Suites et Séries):
 (69.141)
(69.141)
Nous avons alors c'est une approche à la façon ingénieur...:
 (69.142)
(69.142)
Soit:
 (69.143)
(69.143)
où  est
donc un coefficient sans dimensions (comme est
donc un coefficient sans dimensions (comme  ...)
plus facilement mesurable expérimentalement. ...)
plus facilement mesurable expérimentalement.
L'équation de continuité (cf. chapitre
de Thermodynamique) ou
de bilan de masse:
 (69.144)
(69.144)
devient alors:
 (69.145)
(69.145)
au premier ordre en  .
De plus, nous avons montré dans le chapitre de Mécanique des Milieux
Continus que si le fluide est incompressible: .
De plus, nous avons montré dans le chapitre de Mécanique des Milieux
Continus que si le fluide est incompressible:
 (69.146)
(69.146)
Retenons qu'en première approximation le fluide est incompressible.
Il ne reste alors que:
 (69.147)
(69.147)
Comme nous souhaitons étudier un écoulement en présence de gravité,
il serait judicieux de poser:
 (69.148)
(69.148)
et donc de ne s'intéresser qu'aux variations autour de la position
d'équilibre hydrostatique ( est
sans dimensions!). Nous avons démontré toujours dans le même chapitre
de Mécanique des Milieux continus que dans le cas du fluide incompressible
avec viscosité, l'équation d'Euler de 1ère forme (équation
du mouvement): est
sans dimensions!). Nous avons démontré toujours dans le même chapitre
de Mécanique des Milieux continus que dans le cas du fluide incompressible
avec viscosité, l'équation d'Euler de 1ère forme (équation
du mouvement):
 (69.149)
(69.149)
Intéressons-nous dans un premier temps aux deux termes:
 (69.150)
(69.150)
qui s'écrivent selon l'axe Z:
 (69.151)
(69.151)
Lorsqu'il y a mouvement, la projection suivant Z fait
donc apparaître:
 (69.152)
(69.152)
que nous récrivons alors:
 (69.153)
(69.153)
Soit:
 (69.154)
(69.154)
puisque:
 (69.155)
(69.155)
Il vient:
 (69.156)
(69.156)
Il reste donc une force de flottabilité dirigée vers le haut.
La variation de la densité en fonction de la température dans
le produit  de
la relation: de
la relation:
 (69.157)
(69.157)
sera négligée  car
nous nous restreindrons au cas où la vitesse est petite. Nous avons
alors en réintroduisant la viscosité...: car
nous nous restreindrons au cas où la vitesse est petite. Nous avons
alors en réintroduisant la viscosité...:
 (69.158)
(69.158)
et nous avons la dérivée particulaire (cf.
chapitre de Mécanique
des Milieux Continus):
 (69.159)
(69.159)
soit aussi une autre relation utile:
 (69.160)
(69.160)
Nous avons alors comme expression de la densité de force:
 (69.161)
(69.161)
Pour continuer, nous allons chercher à déterminer la loi
d'énergie
de l'équation de comportement démontrée dans
le chapitre de Mécanique
Des Milieux Continus:
 (69.162)
(69.162)
pour qu'elle rende également compte de la relation entre les
contraintes et les caractéristiques thermodynamiques du fluide,
comme le flux de chaleur et la température. Nous allons le faire
en caractérisant la diffusion de l'énergie dans le milieu due aux
effets (supposés découplés) de la viscosité du fluide et de la
conduction thermique du fluide.
Nous réécrivons cette relation avec de nouvelles constantes et
une autre notation pour la divergence:
 (69.163)
(69.163)
où  sont
dans ce contexte appelés les "coefficients
de Lamé". sont
dans ce contexte appelés les "coefficients
de Lamé".
Nous avons aussi démontré dans le chapitre de Mécanique des Milieux
Continus la relation:
 (69.164)
(69.164)
Soit:
 (69.165)
(69.165)
Ce qui donne:
 (69.166)
(69.166)
Notons l'énergie totale comme:
 (69.167)
(69.167)
où e est l'énergie interne massique du fluide (rapportée
donc à une unité de masse de fluide). Or la variation instantanée
d'énergie interne du fluide est égale à l'apport d'une puissance
mécanique et de l'apport de chaleur (selon ce qui a été vu dans
le chapitre de Thermodynamique):
 (69.168)
(69.168)
où P donne la puissance des efforts extérieurs
au système
donnée forcément par la force du champ de potentiel
environnant et des forces mécaniques données par
le tenseur des contraintes uniquement (nous sommes toujours dans
la situation d'un fluide parfait...).
Soit:
 (69.169)
(69.169)
et en utilisant le théorème d'Ostrogradsky (cf.
chapitre de Calcul Vectoriel):
 (69.170)
(69.170)
ce qui a bien les unités d'une puissance et nous avons bien:
 (69.171)
(69.171)
Pour la puissance chaleur  c'est
très facile aussi grâce aux développements que nous avions fait
dans le chapitre de Thermodynamique où nous avons obtenu l'équation
de la chaleur: c'est
très facile aussi grâce aux développements que nous avions fait
dans le chapitre de Thermodynamique où nous avons obtenu l'équation
de la chaleur:
 (69.172)
(69.172)
Soit:
 (69.173)
(69.173)
Nous avons finalement:
 (69.174)
(69.174)
Donc tout cela nous donne alors l'équation de l'énergie d'un
fluide:
 (69.175)
(69.175)
Soit:
 (69.176)
(69.176)
et comme (cf. chapitre de Thermodynamique) le flux de chaleur
suit la loi de Fourier:
 (69.177)
(69.177)
Nous avons alors:
 (69.178)
(69.178)
Soit en utilisant la définition du laplacien d'un champ scalaire:
 [1] [1]
(69.179)
Maintenant, en faisant le produit scalaire de:
 (69.180)
(69.180)
avec la vitesse  nous
obtenons le bilan de l'énergie cinétique: nous
obtenons le bilan de l'énergie cinétique:
 [2] [2]
(69.181)
En soustrayant [2] de [1], nous obtenons une relation locale
de l'énergie interne spécifique e:
 (69.182)
(69.182)
Or, nous avons aussi (dérivation d'un produit):
 (69.183)
(69.183)
Soit:
 (69.184)
(69.184)
Effectivement:

(69.185)
Nous avons donc:
 (69.186)
(69.186)
et comme le tenseur  est
symétrique: est
symétrique:
 (69.187)
(69.187)
Nous avons donc:
 (69.188)
(69.188)
Ce qui est parfois noté:
 (69.189)
(69.189)
où  est
appelé "tenseur des taux de déformation" et est
appelé "tenseur des taux de déformation" et  représente
le produit doublement contracté du tenseur des contraintes
et du tenseur des taux de déformation. représente
le produit doublement contracté du tenseur des contraintes
et du tenseur des taux de déformation.
Nous avons montré dans le chapitre de Mécanique des Milieux Continus:
 (69.190)
(69.190)
où:
 (69.191)
(69.191)
Ainsi, il est simple de différencier forces normales et forces
tangentielles. Bref pour en revenir à l'équation de l'énergie:
 (69.192)
(69.192)
Nous avons donc:
 (69.193)
(69.193)
Mais dans notre cas:
 (69.194)
(69.194)
Soit:
 (69.195)
(69.195)
Mais nous avons:
 (69.196)
(69.196)
Nous avons donc:
 (69.197)
(69.197)
Soit sous forme technique et condensée:
 (69.198)
(69.198)
Il est clair qu'au niveau de l'entropie, nous avons:
 (69.199)
(69.199)
Nous avons aussi:
 (69.200)
(69.200)
Soit réduit au rapport massique:
 (69.201)
(69.201)
La variation temporelle donnant:
 (69.202)
(69.202)
Or, nous avons l'équation de continuité (cf.
chapitre de Thermodynamique):
 (69.203)
(69.203)
Ce qui nous donne finalement:
 (69.204)
(69.204)
ou autrement écrit:
 (69.205)
(69.205)
Injectée dans:
 (69.206)
(69.206)
Cela donne:
 (69.207)
(69.207)
Si nous considérons le gradient de vitesse comme étant très faible
(quasi-statique) nous pouvons alors écrire l'approximation:
 (69.208)
(69.208)
Maintenant donnons l'expression de l'entropie (différentielle
totale exacte) en fonction des paramètres de température et de
pression seuls:
 (69.209)
(69.209)
soit sous forme massique:
 (69.210)
(69.210)
Or nous avons démontré dans le chapitre de Thermodynamique la
relation suivante:
 (69.211)
(69.211)
soit sous forme massique:
 (69.212)
(69.212)
Ce qui nous donne:
 (69.213)
(69.213)
Or, nous avons démontré avec dans le chapitre de Thermodynamique
une des relations de Maxwell:
 (69.214)
(69.214)
soit sous forme massique:
 (69.215)
(69.215)
d'où:
 (69.216)
(69.216)
Soit:
 (69.217)
(69.217)
Soit notre relation:
 (69.218)
(69.218)
peut alors s'écrire:
 (69.219)
(69.219)
Si nous admettons que la variation de la densité avec
la température
est faible, nous avons alors à l'échelle atmosphérique
:
 (69.220)
(69.220)
et en se rappelant que:
 (69.221)
(69.221)
Il vient finalement:
 (69.222)
(69.222)
Nous avons maintenant deux équations importantes:
 (69.223)
(69.223)
Soit:
 (69.224)
(69.224)
Examinons maintenant rapidement le problème de Rayleigh-Bénard
qui consiste en deux plaques limitant un fluide une étant
plus chauffée que l'autre.
Nous pouvons alors observer des rouleaux longitudinaux parallèles
dans un film de fluide visqueux (huile de silicone) maintenus entre
deux plaques à une température chaude en bas et froide en
haut. Voici une photo de ces rouleaux vus de côtés:

Figure: 69.13 - Rouleaux de convection de Rayleigh-Bénard (instabilité)
vue de dessus:

Figure: 69.14 - Instabilités de Rayleigh-Bénard vues du dessus
Il s'agit d'un problème de convection naturelle: le fluide chauffé en
bas se dilate et remonte entraînée par la force d'Archimède, arrivé en
haut il se refroidit et retombe. C'est ce mouvement qu'il faut
expliquer qui est similaire à celui de l'atmosphère terrestre
Nous remarquons également que les mouvements de convection se
font approximativement selon un tore (voir la photo vue de côté).
Nous pouvons tirer parti de cette symétrie pour simplifier l'analyse.
Considérons donc une boucle verticale de fluide circulant à vitesse
constante (donc sans trop de turbulences...):

Figure: 69.15 - Boucle verticale de fluide avec gradient
La configuration sera imposée comme étant la suivante:

Figure: 69.16 - Configuration imposée pour le modèle théorique
où  est
la température moyenne du fluide (attention: ne pas oublier que
ce n'est pas une grandeur extensive!) et où nous avons indiqué respectivement
les températures à l'intérieur du tore et à l'extérieur (soit de
l'environnement) qui peuvent toutes varier en fonction du temps. est
la température moyenne du fluide (attention: ne pas oublier que
ce n'est pas une grandeur extensive!) et où nous avons indiqué respectivement
les températures à l'intérieur du tore et à l'extérieur (soit de
l'environnement) qui peuvent toutes varier en fonction du temps.
Nous voyons que la différence de température est de  entre
le haut et le bas et de entre
le haut et le bas et de  entre
la droite et la gauche. entre
la droite et la gauche.
Nous posons que la température varie linéairement avec la hauteur
(ce qui bien évidemment est faux dans un modèle atmosphérique...):
 (69.225)
(69.225)
Nous remarquons qu'il possible de paramétrer la température
le long de l'intérieur du tore avec la relation suivante
(équation
paramétrique du cercle):
 (69.226)
(69.226)
Nous avons alors conformément au schéma:
 (69.227)
(69.227)
Ceci étant posé, revenons à:
 (69.228)
(69.228)
Nous allons passer ce système en coordonnées polaire correspondant
le mieux à la géométrie de notre problème. Rappelons d'abord que
dans terme:
 (69.229)
(69.229)
l'opérateur différentiel  est
la divergence. Or, nous avons démontré dans le chapitre
de Calcul Vectoriel que celui-ci s'écrivait alors en coordonnées
polaires: est
la divergence. Or, nous avons démontré dans le chapitre
de Calcul Vectoriel que celui-ci s'écrivait alors en coordonnées
polaires:
 (69.230)
(69.230)
Or, si nous nous basons sur l'hypothèse que dans le volume du
tore, la vitesse ne varie ni en fonction de l'angle, ni à l'intérieur
du tore (donc ne varie pas selon le rayon r) alors en coordonnées
polaires:
 (69.231)
(69.231)
Nous avons alors:
 (69.232)
(69.232)
Nous allons réduire l'analyse à une seule dimension
qui sera celle comme quoi le phénomène ne dépend
que de l'angle. Nous avons alors en coordonnées polaires
et en explicitant tous les termes:
 (69.233)
(69.233)
où nous avons fait par la même occasion la projection selon l'axe z tel
que:
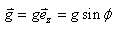 (69.234)
(69.234)
Le coefficient différentiel du dernier terme va nous embêter.
Nous le remplaçons par un coefficient que nous supposerons constant
et qui s'oppose au mouvement tel que nous ayons:
 (69.235)
(69.235)
Ou plus explicitement:
 (69.236)
(69.236)
Nous intégrons maintenant l'ensemble sur l'entier de la boucle
en fonction de  .
Nous avons alors: .
Nous avons alors:
 (69.237)
(69.237)
Nous avons alors le terme pression qui disparaît, car il n'y
a pas de gradient de pression au long de la boucle. Ainsi:
 (69.238)
(69.238)
Nous avons ensuite (cf. chapitre de Calcul
Différentiel Et Intégral):
 (69.239)
(69.239)
et:
 (69.240)
(69.240)
Il nous reste donc:
 (69.241)
(69.241)
Soit:
 (69.242)
(69.242)
Nous voyons dans cette équation que le mouvement est piloté par
la différence de température horizontale  . .
Maintenant, revenons sur:
 (69.243)
(69.243)
Si nous négligeons les forces tangentielles à l'intérieur
de fluide, nous avons alors:
 (69.244)
(69.244)
où D est le coefficient de diffusion thermique (cf.
chapitre de Thermodynamique).
En coordonnées polaires cela se réduit à:
 (69.245)
(69.245)
et nous allons aussi faire une autre approximation:
 (69.246)
(69.246)
Et nous avons les deux relations:
 (69.247)
(69.247)
En soustrayant:
 (69.248)
(69.248)
Soit:
 (69.249)
(69.249)
et encore:
 (69.250)
(69.250)
Soit:
 (69.251)
(69.251)
Après dérivation:
 (69.252)
(69.252)
Nous regroupons les termes:
 (69.253)
(69.253)
Nous avons alors les trois équations différentielles suivantes
qui gouvernent la dynamique du système:
 (69.254)
(69.254)
Nous terminons les multiples simplifications en posant...:

Ce qui nous donne:
 (69.255)
(69.255)
En remettant cela au propre:
 (69.256)
(69.256)
Maintenant, introduisons les variables sans dimensions suivantes:
 (69.257)
(69.257)
où nous pouvons assimiler:
- X à la vitesse adimensionnelle
- Y à la différence adimensionnelle de température entre
courants ascendants et descendants
- Z à la déviation adimensionnelle de l'équilibre de convection.
Nous avons alors effectivement:
 (69.258)
(69.258)
Soit:
 (69.259)
(69.259)
De manière encore plus condensée et traditionnelle:
 (69.260)
(69.260)
où nous avons:
 (69.261)
(69.261)
ce qui correspond au "nombre de Prandtl" et:
 (69.262)
(69.262)
ce qui est assimilé au "nombre de
Rayleigh".
Ce système de trois équations est essentiellement
le même
que celui du célèbre système de Lorenz. À
une différence près,
le système de Lorenz (réel) contient un facteur b dans
la dernière équation (ce qui change peu de toute
façon le résultat
puisque l'on obtient quand même un attracteur étrange au
bout du compte comme nous allons de suite le voir):
 (69.263)
(69.263)
Pr, Re et b sont strictement positifs, et on pose souvent  où le
nombre de Prandtl correspond à la valeur de l'eau. où le
nombre de Prandtl correspond à la valeur de l'eau.
Les équations de Lorenz décrivent les phénomènes de convection
d'un fluide idéal à deux dimensions, dans un réservoir chauffé par
le bas.
Nous voyons par cette démonstration que contrairement aux dires
non démontrés sur Internet que:
1. Le système n'est de loin pas simple mathématiquement et est
très approximatif
2. Qu'il existe des systèmes vraiment plus simples et
eux aussi chaotiques (cf. chapitre de Dynamique
des Populations).
L'intérêt des équations de Lorenz réside
cependant dans la sensibilité aux
conditions initiales et à la convergence des variables adimensionnelles.
Voyons un exemple avec Maple 4.00b:
>with(DEtools):
>lorenz:=diff(x(t),t) = 10*(y(t)-x(t)),diff(y(t),t) = 28*x(t)-y(t)-x(t)*z(t),diff(z(t),t)
= x(t)*y(t)-8/3*z(t);
>DEplot3d({lorenz}, [x(t),y(t),z(t)], t=0..100,
stepsize=0.01, [[x(0)=10, y(0)=10, z(0)=10]], orientation=[-35,75],
linecolor
= t, thickness = 1);
Ce qui donne pour les 100 premières unités de temps
adimensionnel:

Figure: 69.17 - Espace des phases du système des équations de Lorenz
Ou pour les dix premières unités de temps adimensionnel:

Figure: 69.18 - Espace des phases du système des équations de Lorenz
Bon jusque-là on s'en rend compte que les paramètres adimensionnels
tournent autour de deux points que nous appelons les "attracteurs étranges".
Définition: Dans l'étude des systèmes dynamiques, un attracteur
(ou ensemble-limite) est un ensemble, une courbe ou un espace vers
lequel un système évolue de façon irréversible en l'absence de
perturbations.
Maintenant toujours pour les mêmes valeurs du temps adimensionnel,
nous prenons  ,
soit un changement relativement faible des conditions initiales.
Nous avons alors: ,
soit un changement relativement faible des conditions initiales.
Nous avons alors: 
Figure: 69.19 - Petite variation dans les conditions initiales
Nous remarquons donc que le phénomène n'est plus vraiment semblable.
Considérons par exemple la variable x en prenant comme
condition initiale  puis puis  soit
une légère variation de 0.01 sur la valeur de soit
une légère variation de 0.01 sur la valeur de  . .
Soit dans Maple 4.00b:
>DEplot({lorenz}, [x(t), y(t), z(t)], t=0..15, stepsize = 0.01,
[[x(0)=10, y(0)=10, z(0)=10],[x(0)=10, y(0)=10.01, z(0)=10]], scene
= [t,x], linecolor = [blue,green], thickness = 1);

Figure: 69.20 - Analyse de la variable adimensionnée x pour une faible
variation des C.I.
Nous voyons que le système se décale assez rapidement du modèle
initial alors qu'au début il reste identique mais la forme globale
reste.
Autre chose... suivant les paramètres le système peut converger.
Effectivement, en changeant le facteur 28 par la valeur 22 nous
avons par exemple (convergence à gauche):

Figure: 69.21 - Convergence du système
ou avec la valeur 19 le résultat est encore plus trivial:

Figure: 69.22 - Convergence directe
ou encore avec une valeur proche de 1:

Figure: 69.23 - Encore plus rapide
On remarque un dernier cas intéressant, c'est que si le nombre
de Prandtl vaut 1 alors le système est stable:

Figure: 69.24 - Stabilité du système
Cette sensibilité aux conditions initiales, ainsi que
la forme de l'attracteur étrange de Lorenz a amené les
météorologues à faire
une métaphore avec la phrase suivante: le battement d'ailes
d'un papillon au Brésil peut-il provoquer une tornade au
Texas?
(en taisant la dissipation de l'erreur dû aux échelles
considérées...).
D'où la dénomination par la suite de "effet
Papillon" pour
l'étude de l'attracteur de Lorenz appelé aussi dans le domaine
le "papillon de Lorenz".
VAGUES
Quand on se retrouve sur un bateau, le mouvement de l'eau rend
beaucoup de personnes malades. C'est aussi le cas quand on se trouve
dans la galère de calculer ce type de mouvement... En effet, les
vagues dans l'eau ne sont ni des ondes transversales, ni des ondes
longitudinales. Elles sont un peu des deux. Les particules d'eau
décrivent des cercles ou des ellipses, dans un plan vertical parallèle
au déplacement de la vague. Le gros problème est qu'une des conditions
limites se trouve à la surface de l'eau et que l'on ne sait pas
où se trouve cette surface. C'est précisément une des inconnues.
Le problème est assez ardu pour que ce calcul ne figure pas dans
les ouvrages de physique générale ou spécialisés francophones.
Nous avons alors tenté de l'inclure ici en simplifiant énormément
et en ne gardant que les cas les plus simples. Le calcul qui suit
peut être pris comme exemple de la façon comme les physiciens se
simplifient la vie en faisant des approximations et aussi comme
exemple magistral d'un phénomène banal mais complexe à modéliser.
Nous ne calculerons pas l'équation d'onde. Nous devons calculer
le mouvement des particules depuis la surface jusqu'au fond de
l'eau, puisque le mouvement s'étend jusqu'au fond. Mais comme les
particules décrivent des ellipses, il faut au moins deux variables
par point: il nous faut un champ vectoriel. Nous calculerons donc
le champ vectoriel des vitesses des particules, mais nous ne le
calculerons pas directement. Ce que nous allons trouver, c'est
un potentiel scalaire de vitesses dont le gradient sera le champ
vectoriel de vitesses.
Un dernier mot sur les ondes que nous allons calculer. Ces ondes
s'appellent "ondes de gravité", parce que c'est le poids
de l'eau qui sert de force de restitution pour faire descendre
les sommets et remonter les creux.
Je tiens à remercier Monsieur Louis Peralta pour sa maîtrise
mathématique et sa pédagogie sans qui ces développements passionnants
n'auraient jamais pu être présentés sur le site web. Je lui suis
redevable, avec son accord, d'un copier/coller de 99% de son support
de cours.
Nous allons faire des calculs dans le cas le plus simple: des
ondes dans un canal rectiligne de section rectangulaire et de largeur
et profondeur constante. Ceci réduit les dimensions du problème à deux
(puisque la troisième à un profil identique de vague quel que soit
l'endroit où l'on se positionne en largeur): la profondeur et la
direction d'avance des vagues. Bien entendu, nous négligerons la
friction sur le fond ou les parois du canal et... bien d'autres
choses.
Le système de coordonnées choisi est alors:
- x horizontal, positif dans le sens d'avancement des
vagues (sens de la longueur du canal)
- y horizontal dans le sens perpendiculaire à l'avancement
des vagues (sens de la largeur du canal). Encore une fois, aucune
variable ne dépendra de y pour les raisons déjà susmentionnées
- z vertical et positif vers le haut. Le zéro étant choisi à la
surface de l'eau non perturbée. Sous l'eau, z sera donc
négatif. La profondeur du canal étant h, le fond de l'eau
se trouvera alors à 
Maintenant, rappelons que nous avons démontré après de très longs
développements dans le chapitre de Mécanique Des Milieux Continus,
que si le fluide est incompressible (divergence du champ vectoriel
des
vitesses
est
donc nul  )
et que la viscosité dynamique l'est aussi, nous avons alors l'équation
d'Euler de 1ère forme: )
et que la viscosité dynamique l'est aussi, nous avons alors l'équation
d'Euler de 1ère forme:
 (69.264)
(69.264)
car U est pour rappel le potentiel scalaire du champ gravitationnel.
Ce que nous écrirons explicitement sous la forme suivante dans
le cas de notre étude des vagues:
 (69.265)
(69.265)
Avant de continuer, nous allons changer la forme du terme 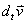 qui
est une dérivée totale et non partielle. Examinons une des deux
composantes (x ou z) de ce terme. Prenons la composante x du
vecteur vitesse et utilisons ce que nous avons vu dans le chapitre
de Calcul Différentiel Et Intégral (nous avons omis la composante y puisque
le système n'en dépend pas): qui
est une dérivée totale et non partielle. Examinons une des deux
composantes (x ou z) de ce terme. Prenons la composante x du
vecteur vitesse et utilisons ce que nous avons vu dans le chapitre
de Calcul Différentiel Et Intégral (nous avons omis la composante y puisque
le système n'en dépend pas):
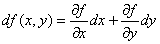 (69.266)
(69.266)
Nous avons dans notre situation:
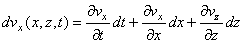 (69.267)
(69.267)
Il vient alors:
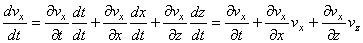 (69.268)
(69.268)
Le premier terme 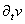 est
un terme linéaire, par contre les trois autres sont des termes
quadratiques (car ils comportent le produit d'une vitesse par la
dérivée d'une vitesse) qui sont une infection dans tous les calculs
formels. Nous allons donc limiter nos calculs aux cas où ces termes
quadratiques sont négligeables devant les termes linéaires (ce
qui signifie implicitement la vitesse doit varier très peu sinon
quoi cette hypothèse n'est plus valable). Avec cette restriction,
nous avons alors: est
un terme linéaire, par contre les trois autres sont des termes
quadratiques (car ils comportent le produit d'une vitesse par la
dérivée d'une vitesse) qui sont une infection dans tous les calculs
formels. Nous allons donc limiter nos calculs aux cas où ces termes
quadratiques sont négligeables devant les termes linéaires (ce
qui signifie implicitement la vitesse doit varier très peu sinon
quoi cette hypothèse n'est plus valable). Avec cette restriction,
nous avons alors:
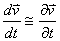 (69.269)
(69.269)
Nous pouvons alors écrire:
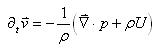 (69.270)
(69.270)
Nous allons rajouter une restriction supplémentaire à nos calculs.
Cette restriction consiste à imposer que le rotationnel de la vitesse
est nul:
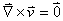 (69.271)
(69.271)
Cela revient à dire, comme nous l'avons vu dans le chapitre de
Mécanique Des Milieux Continus, qu'il n'y a pas de tourbillons
dans l'eau. Nous avions déjà imposé que la vitesse était nulle
dans le sens des y, ce qui empêche les tourbillons verticaux
(axe de rotation vertical). Maintenant nous éliminons la possibilité de
tourbillons avec l'axe de rotation horizontal. Ce n'est pas, en
fait, une trop grande restriction, nous savons qu'un objet abandonné aux
vagues ne tourne pas sur lui-même à moins d'être pris dans des
rouleaux. Dans les cas que nous allons calculer, les amplitudes
sont limitées, nous sommes dans le cas linéaire et, surtout, pas
dans celui des rouleaux.
Nous avons démontré dans le chapitre de Calcul Vectoriel que
lorsque le rotationnel d'une variable vectorielle est nul, la variable
peut être exprimée comme le gradient d'un potentiel scalaire:
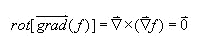 (69.272)
(69.272)
Il vient alors que nous pouvons écrire:
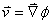 (69.273)
(69.273)
Nous avons alors:
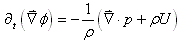 (69.274)
(69.274)
Ce qui peut s'écrire:
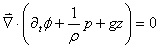 (69.275)
(69.275)
Cette équation tient lieu d'équation d'onde, même si elle ne
décrit pas directement la position ou la vitesse des particules.
Une fois résolue l'équation et la fonction 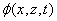 trouvée,
nous pourrons déduire les vitesses: trouvée,
nous pourrons déduire les vitesses:
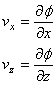 (69.276)
(69.276)
Il ne faudra pas oublier que puisque la divergence du champ vectoriel
des vitesses est nul:
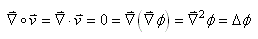 (69.277)
(69.277)
donc le laplacien scalaire de 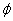 est
nul: est
nul:
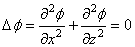 (69.278)
(69.278)
Soit:
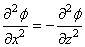 (69.279)
(69.279)
avec 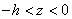 . .
La solution doit satisfaire des conditions limites. La plus évidente
est que la vitesse verticale doit être nulle au fond de l'eau.
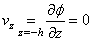 (69.280)
(69.280)
Pour trouver les conditions limites à la surface, nous allons
définir la variable 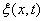 qui
est égale au déplacement vertical d'une particule d'eau située à la
surface de l'eau dont la position d'équilibre (en absence de vagues)
est x (à ne pas confondre avec l'autre x!). La hauteur
de la surface de l'eau, mesurée par référence au niveau de l'eau
sans vague, sera donnée donc par qui
est égale au déplacement vertical d'une particule d'eau située à la
surface de l'eau dont la position d'équilibre (en absence de vagues)
est x (à ne pas confondre avec l'autre x!). La hauteur
de la surface de l'eau, mesurée par référence au niveau de l'eau
sans vague, sera donnée donc par 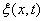 .
Ainsi, la vitesse verticale .
Ainsi, la vitesse verticale 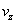 à la
surface de l'eau sera: à la
surface de l'eau sera:
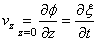 (69.281)
(69.281)
C'est une astuce très subtile et pas évidente du tout à anticiper!
À la surface, nous pouvons considérer que la pression p est
toujours égale à la pression atmosphérique pour toutes les positions
en x et en 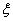 .
Dès lors, à priori rien ne changera si la pression atmosphérique
change, et il est plus commode de la considérer nulle. Avec ceci,
l'équation: .
Dès lors, à priori rien ne changera si la pression atmosphérique
change, et il est plus commode de la considérer nulle. Avec ceci,
l'équation:
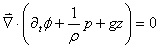 (69.282)
(69.282)
Devient:
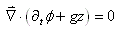 (69.283)
(69.283)
Dont nous déduisons:
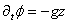 (69.284)
(69.284)
Si nous nous plaçons à la surface, ce qui correspond à 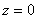 , la
relation précédente devient: , la
relation précédente devient:
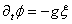 (69.285)
(69.285)
et en dérivant cette dernière relation par rapport au temps,
nous obtenons:
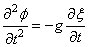 (69.286)
(69.286)
puis en utilisant la relation démontrée juste plus haut:
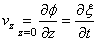 (69.287)
(69.287)
Il vient:
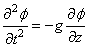 (69.288)
(69.288)
Résumons les conditions que le potentiel scalaire 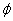 doit
satisfaire: doit
satisfaire:
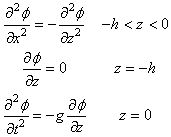 (69.289)
(69.289)
Nous allons chercher seulement des solutions du type séparable
(cf. chapitre de Calcul Différentiel Et Intégral).
C'est-à-dire
que 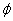 ,
qui est une fonction de x, z et t pourra s'écrire
comme le produit de trois fonctions qui dépendent, chacune, d'une
seule variable. De plus, nous travaillerons seulement en régime
sinusoïdal (une intuition... de l'observation du réel) et en utilisant
le formalisme des phaseurs (cf. chapitre
de Mécanique Ondulatoire).
Dès lors, nous avons: ,
qui est une fonction de x, z et t pourra s'écrire
comme le produit de trois fonctions qui dépendent, chacune, d'une
seule variable. De plus, nous travaillerons seulement en régime
sinusoïdal (une intuition... de l'observation du réel) et en utilisant
le formalisme des phaseurs (cf. chapitre
de Mécanique Ondulatoire).
Dès lors, nous avons:
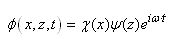 (69.290)
(69.290)
Comme d'habitude, nous retiendrons seulement la partie réelle
des phaseurs des solutions à la fin. Calculons les deuxièmes dérivées
partielles par rapport à x et z:
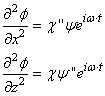 (69.291)
(69.291)
L'équation suivante:
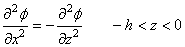 (69.292)
(69.292)
nous dit que sous la surface, ces deux expressions sont égales
au signe près:
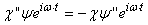 (69.293)
(69.293)
d'où nous déduisons:
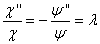 (69.294)
(69.294)
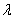 ne
peut être qu'une constante, car les deux côtés de l'expression
dépendent de variables indépendantes (ce qui est très astucieux
comme observation!). Cette constante peut prendre, en principe,
n'importe quelle valeur réelle ou complexe. ne
peut être qu'une constante, car les deux côtés de l'expression
dépendent de variables indépendantes (ce qui est très astucieux
comme observation!). Cette constante peut prendre, en principe,
n'importe quelle valeur réelle ou complexe.
Ce qui nous donne le système de deux équations différentielles
indépendantes du deuxième ordre:
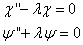 (69.295)
(69.295)
Il s'agit donc d'un système d'équations différentielles linéaire
d'ordre 2 indépendantes, quasiment identique à celui résolu dans
le chapitre de Thermodynamique lorsque nous avons étudié l'équation
de la chaleur.
Ceci étant dit, nous ne connaissons pas le signe de la constante 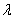 .
Ce que nous savons d'après ce que nous avons étudié dans le chapitre
de Calcul Différentiel Et Intégral c'est que si b est positif
alors la solution de l'équation différentielle en z: .
Ce que nous savons d'après ce que nous avons étudié dans le chapitre
de Calcul Différentiel Et Intégral c'est que si b est positif
alors la solution de l'équation différentielle en z:
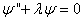 (69.296)
(69.296)
aura des solutions harmoniques. Ce qui serait très surprenant...
et contre intuitif avec ce que nous observons dans la réalité.
Donc nous allons imposer 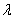 négatif
et dès lors nous avons vu dans le chapitre de Calcul Différentiel
Et Intégral que nous aurons en adoptant à peu près les mêmes écritures: négatif
et dès lors nous avons vu dans le chapitre de Calcul Différentiel
Et Intégral que nous aurons en adoptant à peu près les mêmes écritures:
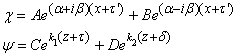 (69.297)
(69.297)
où nous avons le discriminant de la deuxième équation différentielle
(cf. chapitre de Calcul Différentiel Et Intégral) qui vaut:
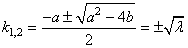 (69.298)
(69.298)
Donc en d'autres termes:
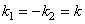 (69.299)
(69.299)
Il vient alors:
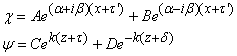 (69.300)
(69.300)
et le discriminant de la première équation différentielle sera
purement complexe:
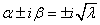 (69.301)
(69.301)
et donc peut s'écrire:
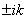 (69.302)
(69.302)
Notre système se simplifie alors encore plus:
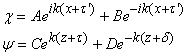 (69.303)
(69.303)
Si nous considérons l'avance (déphasage) nulle nous avons:
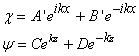 (69.304)
(69.304)
Puisque:
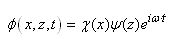 (69.305)
(69.305)
Nous avons:
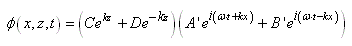 (69.306)
(69.306)
Donc dans la deuxième parenthèse, nous avons simplement deux
vagues qui vont dans des sens opposés. Gardons-en qu'une des deux
pour simplifier l'analyse (peu importe laquelle!):
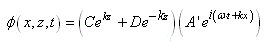 (69.307)
(69.307)
Pour déterminer les constantes, nous allons utiliser la condition
limite donnée plus haut:
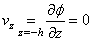 (69.308)
(69.308)
ce qui nous donne dans le cas présent:
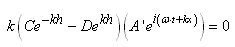 (69.309)
(69.309)
Alors évidemment nous n'allons pas simplifier totalement de manière à avoir K étant
nul sinon cela ne correspondrait pas avec la réalité. Par contre,
nous allons simplifier de la manière suivante:
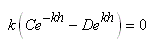 (69.310)
(69.310)
ce qui impose dans le cas non trivial que:
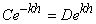 (69.311)
(69.311)
Nous pouvons donc choisir ce que nous voulons, mais si nous
souhaitons nous simplifier la vie en anticipant ce qui va venir...
il vaudrait mieux prendre le choix suivant:
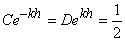 (69.312)
(69.312)
Dès lors:
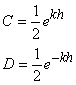 (69.313)
(69.313)
Ainsi, il vient:
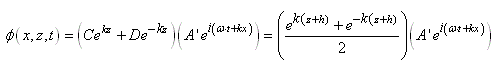 (69.314)
(69.314)
En utilisant les fonctions hyperboliques (cf.
chapitre de Trigonométrie)
nous avons:
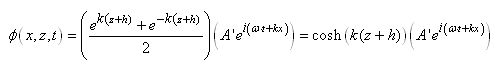 (69.315)
(69.315)
Nous allons continuer à tenter de déterminer les constantes en
utilisant la deuxième condition limite:
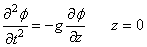 (69.316)
(69.316)
Il vient alors (pour la dérivée du cosinus hyperbolique voir
le chapitre de Calcul Différentiel Et Intégral):
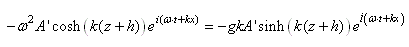 (69.317)
(69.317)
et en posant donc 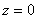 : :
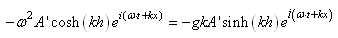 (69.318)
(69.318)
et en simplifiant:
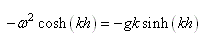 (69.319)
(69.319)
ou autrement écrit:
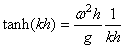 (69.320)
(69.320)
En se rappelant que (cf. chapitre de Mécanique Ondulatoire):
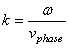 (69.321)
(69.321)
La relation antéprécédente n'a pas à ma
connaissance de solutions permettant d'exprimer directement la
vitesse de phase à partir
d'une expression analytique (elle est donc transcendante) fonction
de la profondeur h et de la fréquence (implicitement
la pulsation) de la vague sans passer un développement de
Maclaurin (cf. chapitre de Suites Et Séries)
de la tangente hyperbolique pour de petites valeurs de kh telles
que:
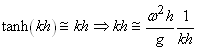 (69.322)
(69.322)
d'où nous tirons donc lorsque la profondeur et k aussi
sont petits en faisant une simplification élémentaire de la relation
précédente:
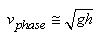 (69.323)
(69.323)
Relation qui est appelée "formule
de Lagrange". Par exemple, pour un tsunami, les longueurs
d'onde sont immenses (de l'ordre de la centaine de kilomètres) donc
le produit hk est petit (de l'ordre de 0.25 dans les océans).
Si au contraire la profondeur h est
très grande ainsi que k nous avons alors en développant
en série de Taylor (cf. chapitre de
Suites Et Séries):
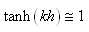 (69.324)
(69.324)
d'où nous tirons alors aussi après une simplification élémentaire:
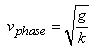 (69.325)
(69.325)
Relation qui est appelée "formule
de Newton".
Cependant nous pouvons résoudre numériquement la
relation: 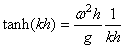 (69.326)
(69.326)
et nous avons alors:

Figure: 69.25 - Espace des phases du système des équations de Lorenz Source: LPFR
Nous pouvons en observant ce graphique comprendre pourquoi les
vagues se brisent (flux supercritique). Effectivement, puisque
la vitesse de phase pour une période donnée augmente
en fonction de la profondeur h,
la partie supérieure de la vague va plus vite que la partie
inférieure
et finit donc pas s'effondrer faute de support. La partie supercritique
de la vague est destructrice dans le cas des tsunamis car elle
l'eau est accélérée dans sa chute par la gravité.
Il en découle aussi que les plus grandes vagues rattrapent les
petites et que leurs amplitudes se superposent sur une certaine
distance. Nous déterminerons plus loin la fonction reliant l'amplitude
de la vague à la distance.
Revenons maintenant sur:
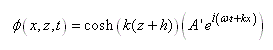 (69.327)
(69.327)
en ne conservant que la partie réelle:
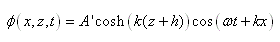 (69.328)
(69.328)
Rappelons que nous avons vu au début:
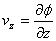 (69.329)
(69.329)
Pour obtenir Z il faut donc dériver la relation antéprécédente
par rapport à z, puis intégrer le résultat par rapport au
temps.
La dérivée donne donc:
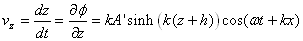 (69.330)
(69.330)
Soit:
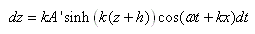 (69.331)
(69.331)
La primitive donne:
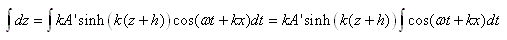 (69.332)
(69.332)
Soit:
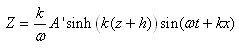 (69.333)
(69.333)
Or nous avons vu au début de notre étude qu'en nous plaçant en 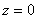 nous
avions donc en surface: nous
avions donc en surface:
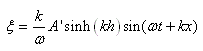 (69.334)
(69.334)
et en notant R l'amplitude de la vague:
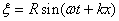 (69.335)
(69.335)
Avec ceci le déplacement vertical Z devient:
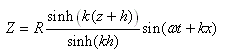 (69.336)
(69.336)
et en se rappelant que le potentiel de vitesses est donné par:
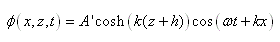 (69.337)
(69.337)
Nous avons avec cette nouvelle constante R:
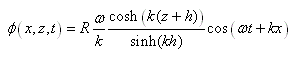 (69.338)
(69.338)
La vitesse horizontale d'une particule d'eau sera alors:
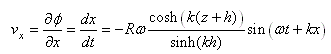 (69.339)
(69.339)
et le déplacement horizontal sera l'intégrale de la relation
précédente par rapport au temps:
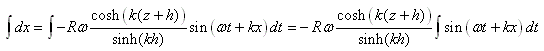 (69.340)
(69.340)
Soit:
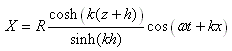 (69.341)
(69.341)
et à la surface en 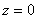 : :
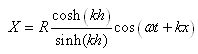 (69.342)
(69.342)
PROFONDEUR DES VAGUES
Il est maintenant intéressant de calculer la profondeur de pénétration
de la vague. En effet, nous savons par vécu que les vagues se font
sentir de moins en mois à mesure que l'on s'enfonce dans l'eau.
Rappelons que nous avons donc:
 (69.343)
(69.343)
qui correspond au déplacement vertical de la vague. Si:
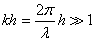 (69.344)
(69.344)
où nous considérerons que la longueur d'onde des vagues est petite
et que la profondeur h du milieu dans lequel elles se propagent
est grande.
Nous avons alors:
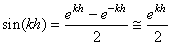 (69.345)
(69.345)
et:
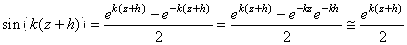 (69.346)
(69.346)
et nous voyons que pour que cette approximation soit satisfaite,
il faut que:
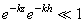 (69.347)
(69.347)
Donc pour que la suite des calculs soit valable, nous imposerons
de petites valeurs de z (donc près de la surface).
Dès lors:
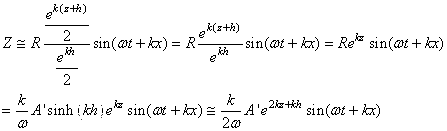 (69.348)
(69.348)
Sans oublier que 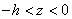 (donc z est
négatif pour rappel!). L'amplitude des mouvements diminue donc
exponentiellement dans ces conditions avec la profondeur. Le lecteur
pourra par contre vérifier que pour certaines valeurs de kh petites,
nous avons: (donc z est
négatif pour rappel!). L'amplitude des mouvements diminue donc
exponentiellement dans ces conditions avec la profondeur. Le lecteur
pourra par contre vérifier que pour certaines valeurs de kh petites,
nous avons:
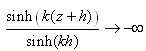 (69.349)
(69.349)
ce qui montre les limites du modèle avec cette approche.
AMPLITUDE DES VAGUES
Pour l'amplitude du mouvement horizontal la situation est la
même. C'est-à-dire pour:
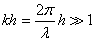 (69.350)
(69.350)
où nous considérerons que la longueur d'onde des vagues est petite
et que la profondeur h du milieu dans lequel elles se propagent
est grande.
Comme nous avons:
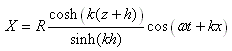 (69.351)
(69.351)
il vient alors:
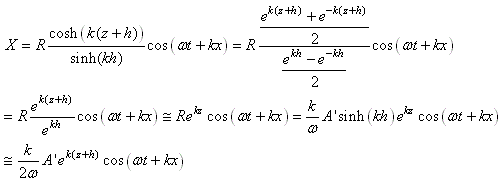 (69.352)
(69.352)
où pour rappel, nous avons toujours 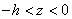 et
que ce modèle n'est valable que près de la surface. et
que ce modèle n'est valable que près de la surface.
Donc pour ces deux approximations, nous avons alors lorsque z est
petit en valeur absolue par rapport à h (donc en eau peu
profonde):
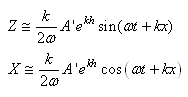 (69.353)
(69.353)
Ainsi, nous pouvons observer que pour le cas de 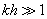 et
en eau peu profonde (pour z petit), les particules d'eau
décrivent un mouvement circulaire (puisque les deux composantes Z et X ont
même amplitude). et
en eau peu profonde (pour z petit), les particules d'eau
décrivent un mouvement circulaire (puisque les deux composantes Z et X ont
même amplitude).
Par contre, dans le cas général, nous avons:
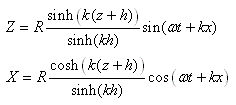 (69.354)
(69.354)
Les amplitudes ne sont dès lors plus les mêmes et les mouvements
sont alors elliptiques.

- Dynamics of the Atmosphere (A
course in Theoretical Meterology),W. Zdunkowski
+ A. Bott, Éditions Cambridge, ISBN10:
052100666X (738 pages)- Imprimé en 2003
 14 14  0 0 |
Commentaires:
Warning: mysql_connect() [function.mysql-connect]: [2002] Connection refused (trying to connect via tcp://crawl809.us.archive.org:3306) in /home/www/f9f6c3f0bb515fb7fa59d2c99a31acd3/web/htmlfr/php/commentaires/config/fonctions.lib.php on line 46
Warning: mysql_connect() [function.mysql-connect]: Connection refused in /home/www/f9f6c3f0bb515fb7fa59d2c99a31acd3/web/htmlfr/php/commentaires/config/fonctions.lib.php on line 46
Warning: mysql_select_db() expects parameter 2 to be resource, boolean given in /home/www/f9f6c3f0bb515fb7fa59d2c99a31acd3/web/htmlfr/php/commentaires/config/fonctions.lib.php on line 47
Warning: mysql_query() expects parameter 2 to be resource, boolean given in /home/www/f9f6c3f0bb515fb7fa59d2c99a31acd3/web/htmlfr/php/commentaires/config/fonctions.lib.php on line 50
Warning: mysql_fetch_array() expects parameter 1 to be resource, null given in /home/www/f9f6c3f0bb515fb7fa59d2c99a31acd3/web/htmlfr/php/commentaires/config/fonctions.lib.php on line 51
[] 
Warning: mysql_close() expects parameter 1 to be resource, boolean given in /home/www/f9f6c3f0bb515fb7fa59d2c99a31acd3/web/htmlfr/php/commentaires/config/fonctions.lib.php on line 58
|
|