|

TRIGONOMÉTRIE
| GÉOMÉTRIE EUCLIDIENNE
| GÉOMÉTRIES
NON-EUCLIDIENNES
GÉOMÉTRIE
PROJECTIVE | GÉOMÉTRIE
ANALYTIQUE | GÉOMETRIE
DIFFÉRENTIELLE
FORMES GÉOMÉTRIQUES
| THÉORIE DES GRAPHES
La
géométrie est la discipline mathématique ayant pour objet l'étude
rigoureuse des espaces et des formes.
(Larousse)
Dernière mise à jour de ce chapitre:
2017-12-31 17:59:07 | {oUUID 1.786}
Version: 3.2 Révision 11 | Avancement: ~100%
 vues
depuis le 2012-01-01: 56'538 vues
depuis le 2012-01-01: 56'538
 LISTE
DES SUJETS TRAITÉS SUR CETTE PAGE LISTE
DES SUJETS TRAITÉS SUR CETTE PAGE
La trigonométrie
fait partie intégrante
de la science de la géométrie. La géométrie
ayant pour racine étymologique "mesure
de la terre" la trigonométrie a elle pour racine étymologique "mesure
des corps à trois angles (trigones)".
Remarques:
R1. Il
existe actuellement trois trigonométries connues (définies)
couramment utilisées en mathématique: la trigonométrie
du cercle (assimilée à l'étude des "fonctions
circulaires"), la
trigonométrie
hyperbolique et la trigonométrie
sphérique.
Nous proposons dans le présent texte une tentative d'approche
relativement rigoureuse de toutes les relations les plus connues
dans ces trois domaines.
R2. Nous
ne traiterons par contre pas ici des trigonométries quadratique
et rhombique qui sont utilisées par les électroniciens
et qui n'ont peu voire pas d'intérêt en physique théorique.
La même remarque est
valable pour la trigonométrie lemniscatique qui est en
relation avec la mathématique pure et en particulier
la fonction zêta de Riemann.
R3. Le lecteur qui chercherait la démonstration des dérivées
et intégrales des fonctions trigonométriques définies
ci-après devra se reporter au chapitre de Calcul Différentiel
Et Intégral (cf. section d'Algèbre)
où les dérivées et intégrales des
fonctions usuelles que nous pouvons trouver dans les formulaires
sont toutes
démontrées.
Le but de ce chapitre va être de déterminer les relations
les plus courantes dans la trigonométrie et qui sont énormément
utilisées
dans tous les chapitres du site (Mécanique, Astronomie,
Statistiques, etc.). Signalons que la majorité des relations
(mais pas
toutes!) que nous allons démontrer ont été déterminées
au 16ème siècle par des algébristes
comme Viète.
RADIAN
Quand nous parlons
de trigonométrie, la première chose qui devrait venir à l'esprit
et s'imposer comme standard de mesures d'angles plans
(voir le chapitre de géométrie plane pour la définition
du concept d'angle) est la notion de "radians".
Définition: 1 "radian" (noté [rad]) est l'angle plan décrit
par une sécante à un cercle,
passant par son centre, tel que l'arc de cercle ainsi défini par
l'axe horizontal passant par le centre du cercle et la sécante
soit d'égale longueur au rayon de ce cercle.
Par exemple, pour un cercle de rayon  donc
de circonférence (ou périmètre P) donc
de circonférence (ou périmètre P)  la
longueur de l'arc de cercle défini par une sécante
ayant un angle de 1 radian par rapport à l'horizontale passant
par le centre du cercle sera égale à 1. la
longueur de l'arc de cercle défini par une sécante
ayant un angle de 1 radian par rapport à l'horizontale passant
par le centre du cercle sera égale à 1.
Dès lors il vient
que l'angle pour "un tour" du cercle sera de:
 (20.1)
(20.1)
L'exemple précédent
se généralise à un cercle de rayon R quelconque
car l'angle pour un tour complet sera toujours  , pour
un demi-tour de , pour
un demi-tour de  et pour
un quart de et pour
un quart de  ... ...
Malheureusement
dans les écoles, les professeurs du primaire apprennent encore aux
enfants à mesurer les angles en degrés. Heureusement la conversion
à faire n'est pas trop difficile... (c'est une simple règle de trois).
Soient r
la mesure d'un angle en radians, d
la mesure du même angle en degrés et g
la mesure du même angle en grades (vieille unité) nous avons
par définition:
 (20.2)
(20.2)
Les astronomes et
les astrophysiciens aiment bien parler en minutes ou secondes d'arc
telles que:
 (minutes d'arc) (minutes d'arc)
 (secondes
d'arc)
(20.3) (secondes
d'arc)
(20.3)
TRIGONOMÉTRIE
DU CERCLE
Soit la figure
ci-dessous représentant un cercle quelconque centré à l'origine
dans une base directe:

Figure: 72.1 - Principe de construction des fonctions trigonométriques élémentaires
De par l'application du théorème
de Pythagore (cf. chapitre de Géométrie
Euclidienne), nous y avons:
 (20.4)
(20.4)
avec R étant
le rayon du cercle.
A partir
de cette représentation, nous pouvons définir
des êtres mathématiques
nommés "fonctions trigonométriques
du cercle", appelés aussi parfois par
les anciens (...) "fonctions cyclométriques,"
tels que (pour les plus importants):
 (20.5)
(20.5)
Il faut faire attention car suivant les auteurs arccos,
arcsin et arctan peuvent être notés respectivement
cos-1,
sin-1, tan-1 .
Remarques:
R1. Lisez "cosinus" pour
"cos", "sinus"
pour "sin", "tangente"
pour "tan", "cotangente"
pour "cot", "sécante"
pour "sec", "cosécante"
pour "csc".
R2. Lorsque le contexte le permet et qu'il ne peut y avoir d'ambiguïté,
les parenthèses après le nom de la fonction trigonométrique
peuvent être omises (c'est souvent le cas en physique).
R3. Les fonctions arc... sont donc les fonctions réciproques des
fonctions trigonométriques (fonctions bijectives) correspondantes!
Attention!! Dans la pratique il ne faut pas oublier que si le
signe de la parenthèse de l'arc tangente est négatif,
nous ne savons alors pas avec exactitude dans quel quadrant (I,
II, III ou IV) nous sommes si nous ne connaissons pas le signe
du numérateur
ou dénominateur! C'est pour cette raison que les calculatrices
ont deux arc tangentes: arctan et arctan2. La première donne un angle
entre 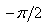 et et 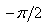 donc
nous ne pouvons pas savoir avec précision dans quel quadrant nous
sommes. La deuxième nous donne un angle entre donc
nous ne pouvons pas savoir avec précision dans quel quadrant nous
sommes. La deuxième nous donne un angle entre 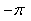 et et 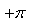 et
donc nous pouvons savoir dans quel quadrant nous sommes. et
donc nous pouvons savoir dans quel quadrant nous sommes.
A partir de
ces fonctions, nous pouvons faire des combinaisons et tirer des
relations remarquables très simples mais dont l'utilité profonde
est discutable (et qui sont très très peu utilisées)
telles que:
 (20.6)
(20.6)
mais vous ne les rencontrerez jamais sur ce site Internet car
je ne fais personnellement jamais usage de cette notation (c'est
plutôt d'usage dans certains ouvrages américains).
Dont voici un superbe schéma... qui résume le tout:

Figure: 72.2 - Principe de construction de toutes les fonctions trigonométriques
Propriétés:
P1. Si nous nous plaçons dans l'étude
du cercle dit "cercle trigonométrique",
il faut poser pour les définitions ci-dessus  .
Ainsi, apparaît plus nettement le sens physique de ces définitions
et il en découlera un nombre de propriétés et d'applications
directement exploitables dans la physique théorique et la mathématique
pure. .
Ainsi, apparaît plus nettement le sens physique de ces définitions
et il en découlera un nombre de propriétés et d'applications
directement exploitables dans la physique théorique et la mathématique
pure.
Effectivement, si  nous
avons trivialement: nous
avons trivialement:
 (20.7)
(20.7)
et en appliquant le théorème
de Pythagore (cf. chapitre de Géométrie
Euclidienne):
 (20.8)
(20.8)
d'où:
 (20.9)
(20.9)
P2. Si  est
un réel, et est
un réel, et  ,
les réels ,
les réels  et et
 sont
associés au même point M de
par la périodicité du cercle trigonométrique. En effet, sont
associés au même point M de
par la périodicité du cercle trigonométrique. En effet,  et et
 sont deux mesures du même angle orienté. Ainsi:
sont deux mesures du même angle orienté. Ainsi:
 (20.10)
(20.10)
Idem
pour toutes les fonctions trigonométriques qui découlent de
la définition
des fonctions sinus et cosinus.
Remarque: Dans la mesure des " angles
orientés", nous disons que deux mesures sont
congrues modulo 
si et seulement si leur différence est un multiple de  .
Cela caractérise deux mesures d'un même angle.
Par définition, le sinus
et le cosinus de tout nombre réel font partie de l'intervalle  . Plus précisément, la position de M nous
permet d'en savoir plus sur le cosinus et le sinus de
. Plus précisément, la position de M nous
permet d'en savoir plus sur le cosinus et le sinus de  .
Ainsi: .
Ainsi:

Figure: 72.3 - Valeurs des angles remarquables des fonctions trigonométriques connues
Il existe également une
autre représentation des fonctions trigonométriques
du cercle, un peu plus technique au sens visuel mais assez importante
pour
bien
comprendre, plus tard, la mécanique ondulatoire:

Figure: 72.4 - Tracé de quelques fonctions trigonométriques usuelles
Le lecteur devrait à ce point remarquer sans
trop de peine les propriétés suivantes (très
souvent utilisées en physique!):
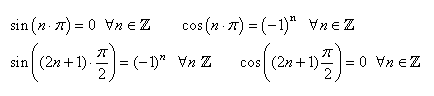 (20.11)
(20.11)
et reconnaître facilement que le sinus est
une fonction impaire et la fonction cosinus une fonction paire
(constat qui
nous sera souvent utile dans divers développements mathématiques
sur les séries trigonométriques).
Nous avons
vu au début de ce chapitre, que de par la définition des fonctions
trigonométriques nous avons:
 (20.12)
(20.12)
et également:
 (20.13)
(20.13)
De façon exactement
identique nous démontrons que:
 (20.14)
(20.14)
A
partir de ces dernières relations nous tirons sans trop de peine
que:
 (20.15)
(20.15)
identiquement
nous aurons:
 (20.16)
(20.16)
par
le raisonnement inverse nous tirons
tout aussi facilement que:
 et et  (20.17)
(20.17)
Il vient également
sans difficultés en observant le cercle trigonométrique que:
 (20.18)
(20.18)
Voici
les schémas qui résument la manière d'analyser
quelques-unes de ces propriétés (pour les autres
relations, la méthode est identique):

Figure: 72.5 - Représentation graphique des équivalences de quelques fonctions trigonométriques
Voici quelques angles remarquables avec les valeurs associées
des cosinus et sinus que beaucoup d'étudiants doivent apprendre
par coeur lors de leurs études:

Figure: 72.6 - Quelques angles et valeurs trigonométriques associées classiques
Introduisons maintenant une dernière relation que nous retrouvons
en optique ondulatoire ou encore dans le cadre des transformées
de Fourier qui est le "sinus cardinal":
 (20.19)
(20.19)
représenté par:

Figure: 72.7 - Tracé de la fonction sinus cardinal
C'est surtout sa forme 3D qui est connue car souvent utilisée
pour des raisons de marketing faisant penser à une goutte
d'eau tombant dans un récipient
d'eau (avec Maple 4.00b) et c'est toujours joli à regarder...:
>plot3d(sin(sqrt(x^2+y^2))/(sqrt(x^2+y^2)),x=-20..20,y=-20..20);

Figure: 72.8 - Tracé de la fonction sinus cardinal en trois dimensions
RELATIONS
REMARQUABLES
Le
dessin ci-dessous va nous permettre d'établir des relations qui
permettront de résoudre des équations impliquant des fonctions trigonométriques
(toutes ces relations sont de première importance en physique pour
la simplification de la résolution de problèmes).

Figure: 72.9 - Construction de base pour la détermination des relations remarquables
Nous
noterons sur le schéma la relation suivante: 
Donc:
 (20.20)
(20.20)
En
résumé:
 (20.21)
(20.21)
Ce
qui implique trivialement si  : :
 (20.22)
(20.22)
et:
 (20.23)
(20.23)
d'où:
 (20.24)
(20.24)
Nous
avons également:
 (20.25)
(20.25)
d'où:
 (20.26)
(20.26)
Ce
qui implique trivialement si  : :
 (20.27)
(20.27)
Avec
la relation déjà démontrée
 nous obtenons également les relations très importantes:
nous obtenons également les relations très importantes:
 (20.28)
(20.28)
Relations
avec lesquelles nous obtenons très facilement les "formules
de Carnot":
 (20.29)
(20.29)
et:
 (20.30)
(20.30)
d'où:
 (20.31)
(20.31)
Nous
avons aussi:
 (20.32)
(20.32)
Ceci,
pour en arriver à la relation:
 (20.33)
(20.33)
qui
implique:
 (20.34)
(20.34)
et
évidemment:
 (20.35)
(20.35)
d'où:
 (20.36)
(20.36)
Nous
obtenons également de manière triviale à partir des
relations précédentes
(nous faisons un petit mélange et nous secouons...):
 et et
 (20.37)
(20.37)
Nous avons aussi:
 (20.38)
(20.38)
avec:
 (20.39)
(20.39)
d'où:
 (20.40)
(20.40)
de manière similaire
nous obtenons:
 (20.41)
(20.41)
avec:
 (20.42)
(20.42)
d'où:
 (20.43)
(20.43)
Déterminons
maintenant les formules trigonométriques complémentaires appelées
"formules de Simpson" ou "formules
d'addition" qui permettent d'exprimer la somme de sinus
et/ou de cosinus en produit de sinus et/ou cosinus.
Soient les relations
déjà démontrées
précédemment:
(1)

(2)

(20.44)
Posons
 et et
 d'où: d'où:
 et et  (20.45)
(20.45)
Nous
obtenons par sommation de (1) et (2):
 (20.46)
(20.46)
et
par différence:
 (20.47)
(20.47)
De
la même manière nous obtenons:
 (20.48)
(20.48)
et
par différence:
 (20.49)
(20.49)
et
inversement nous retombons très facilement sur les relations:
 (20.50)
(20.50)
Toutes ces relations nous seront utiles lors de
notre étude de la physique générale (dans
le chapitre de Mécanique Ondulatoire en particulier et donc
in extenso en Électrodynamique et Acoustique) et particulièrement
dans le cas de calculs d'intégrales ou de superposition
d'ondes.
Remarque: Pour résumer, les relations
suivantes démontrées précédemment:
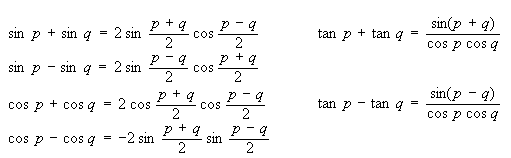 (20.51)
(20.51)
sont donc appelées "formules
de Simpson".
THÉORÈME
DU COSINUS
Démontrons
encore le théorème du cosinus qui nous sera très
utile dans les sections de Géométrie,
Cosmologie, d'Électrodynamique et de Mécanique.
Dans
un triangle quelconque, le carré de l'un des trois côtés
est égal à
la somme des carrés des deux autres diminuée du double
produit de ces deux côtés
par le cosinus de l'angle compris entre eux:

Figure: 72.10 - Construction pour la démonstration du théorème du cosinus
Démonstration:
 (20.52)
(20.52)
mais
dans le triangle ABH,
rectangle en H,
nous avons la relation  d'où: d'où:
 (20.53)
(20.53)
Nous
obtenons donc une des relations du "théorème du cosinus":
 (20.54)
(20.54)
Par
permutation circulaire, nous obtenons les deux autres relations
connues.
Remarque: Le théorème du cosinus est parfois
appelé "formule d'Al-Kashi";
par ailleurs si a est l'hypoténuse et son angle opposé un
angle droit tel que  est
nul, nous retrouvons donc le théorème de Pythagore.
Voici pourquoi nous appelons parfois la formule d'Al-Kashi "formule
de Pythagore généralisée". est
nul, nous retrouvons donc le théorème de Pythagore.
Voici pourquoi nous appelons parfois la formule d'Al-Kashi "formule
de Pythagore généralisée".
Un cas intéressant d'application du théorème
du cosinus est de déterminer la distance l entre
un point b situé sur la circonférence du cercle et un
point a situé
à l'intérieur
du cercle en fonction de la direction (angle) dans
laquelle le regard se porte:

Figure: 72.11 - Distance d'un point à l'intérieur d'un cercle à sa circonférence
Nous pouvons donc appliquer le théorème du cosinus qui nous donne
alors (connaissant d, R et 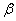 ): ):
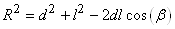 (20.55)
(20.55)
d'où:
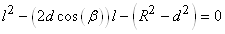 (20.56)
(20.56)
Il s'agit donc d'une équation du deuxième degré dont le discriminant
est:
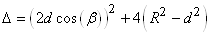 (20.57)
(20.57)
et dont les deux solutions sont:
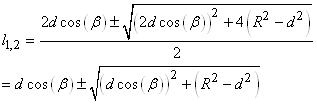 (20.58)
(20.58)
Nous verrons également un cas d'application important
dans le chapitre Formes Géométriques pour calculer la surface d'un
triagnle quelconque (formule de Héron).
THÉORÈME
DU SINUS
Soit
le triangle quelconque dont nous traçons deux hauteurs:

Figure: 72.12 - Construction pour la démonstration du théorème
du sinus
Dans le triangle ci-dessus
nous avons les relations:
 (20.59)
(20.59)
ce qui nous conduit à
l'expression:
 (20.60)
(20.60)
d'où:
 (20.61)
(20.61)
Par un raisonnement similaire
nous avons:
 (20.62)
(20.62)
Ce qui donne:
 (20.63)
(20.63)
Le tout combiné nous
fournit le "théorème des
sinus" dont le plus bel exemple d'application sur ce
site est certainement la détermination des points de Lagrange
L4 et L5 dans le chapitre d'astronomie:
 (20.64)
(20.64)
Évidemment,
il n'y a pas ici toutes les relations trigonométriques (du cercle)
existantes comme nous l'avons déjà dit, mais au moins les plus
importantes qu'il faut savoir retrouver lors de l'étude de systèmes
physiques.
TRIGONOMÉTRIE
HYPERBOLIQUE
Nous
avons démontré dans le chapitre d'Analyse Fonctionnelle
que toute fonction
f(x) peut se décomposer en une fonction
paire et impaire telle que:
 (20.65)
(20.65)
Ainsi,
pour la fonction  ,
nous obtenons: ,
nous obtenons:
 (20.66)
(20.66)
Rappelons que lors de notre étude des nombres complexes
(cf. chapitre Nombres) nous avons
démontré
les formules d'Euler suivantes (qui généralisait les fonctions
trigonométriques à des fonctions allant de  dans dans  ): ):
 (20.67)
(20.67)
Nous
définissons alors par analogie le sinus et le cosinus hyperbolique
(nous démontrerons la provenance de ce terme plus loin) par:
 (20.68)
(20.68)
et
nous pouvons donc écrire:
 (20.69)
(20.69)
Relation
que nous pouvons à nouveau mettre en analogie avec:
 (20.70)
(20.70)
Chose intéressante, nous pouvons travailler en trigonométrie
avec des angles complexes!!
Effectivement, si nous posons  ,
nous avons alors: ,
nous avons alors:
 (20.71)
(20.71)
Or:
 (20.72)
(20.72)
Donc:
 (20.73)
(20.73)
Donc
la fonction hyperbolique d'un angle complexe existe et l'image en
est un nombre complexe aussi. Nous pouvons ainsi voir abusivement
la géométrie hyperbolique comme une sorte de généralisation de la
trigonométrie du cercle aux angles réels et complexes.
Par
opposition à la trigonométrie du cercle, le lecteur remarquera et
vérifiera facilement que nous avons:
 (20.74)
(20.74)
Démonstration:

Nous avons donc:

 C.Q.F.D. C.Q.F.D.
Recherchons maintenant les fonctions réciproques des fonctions
sinus et cosinus hyperboliques (que nous utiliserons parfois en
physique ou en mécanique). Pour cela rappelons que:  (20.75)
(20.75)
et que la recherche de la fonction réciproque consiste toujours à isoler x.
Donc:
 (20.76)
(20.76)
c'est-à-dire:
 (20.77)
(20.77)
en résolvant ce polynôme du deuxième degré en  puis
en prenant le logarithme nous obtenons: puis
en prenant le logarithme nous obtenons:
 (20.78)
(20.78)
Or comme  nous
devons rejeter la solution avec le signe "-". Il vient
alors: nous
devons rejeter la solution avec le signe "-". Il vient
alors:
 (20.79)
(20.79)
d'où:
 (20.80)
(20.80)
En procédant de même pour:
 (20.81)
(20.81)
Donc:
 (20.82)
(20.82)
c'est-à-dire:
 (20.83)
(20.83)
en résolvant ce polynôme du deuxième degré en  puis
en prenant le logarithme nous obtenons: puis
en prenant le logarithme nous obtenons:
 (20.84)
(20.84)
Or comme  nous
devons rejeter la solution avec le signe "-". Il vient
alors: nous
devons rejeter la solution avec le signe "-". Il vient
alors:
 (20.85)
(20.85)
d'où:
 (20.86)
(20.86)
Ainsi:
 (20.87)
(20.87)
Attention car suivant les auteurs arccosh, arcsinh se notent argcosh,
argsinh ou encore cosh-1, sinh-1 .(cette
dernière écriture pouvant prêter à confusion avec l'inverse la
fonction hyperbolique correspondante!).
Pour étudier une représentation géométrique
simple posons maintenant:
 (20.88)
(20.88)
avec
une restriction à  et
donc: et
donc:
 (20.89)
(20.89)
Donc
nous pouvons écrire:
 (20.90)
(20.90)
Or,
comme nous le verrons lors de notre étude des coniques dans le
chapitre de Géométrie Analytique:
1.
La première de ces deux relations, constitue pour l'ensemble de
définition donné, un cercle de rayon unité centré à l'origine.
Le lecteur remarquera qu'il est assez curieux pour la trigonométrie
du cercle d'obtenir un cercle...
2.
La deuxième de ces deux relations, constitue pour l'ensemble
de définition donné, une hyperbole équilatérale orientée
selon l'axe
X dont
le sommet est S(1,0)
et de foyer  .
Le lecteur remarquera à nouveau qu'il est assez curieux pour la
trigonométrie
hyperbolique d'obtenir une hyperbole... .
Le lecteur remarquera à nouveau qu'il est assez curieux pour la
trigonométrie
hyperbolique d'obtenir une hyperbole...
Ces
deux dernières constations devraient permettre, nous l'espérons,
au lecteur de comprendre l'origine du nom de la trigonométrie hyperbolique
et de constater que l'étude la trigonométrie hyperbolique sur l'hyperbole
est l'analogue de l'étude de la trigonométrie du cercle sur le cercle.
Si
nous représentons le cercle trigonométrique et l'hyperbole
trigonométrique
et rajoutons quelques informations complémentaires, voici
ce que nous obtenons:

Figure: 72.13 - Définition des fonctions trigonométriques hyperboliques
Explications:
Pour
tracer à la règle et au compas le point P(x,y) de
l'hyperbole, nous nous donnons x,
donc le point A(x,0).
Nous traçons la tangente au cercle (C) qui
passe par A(x,0) ce
qui nous donne le point de tangence T.
Nous traçons le cercle (G) de
centre A(x,0) et
passant par T.
Ce cercle coupe l'hyperbole au point P(x,y) à
la perpendiculaire en A(x,0) à
Ox.
Nous
voyons apparaître sur la figure plusieurs valeurs des fonctions
hyperboliques correspondant à  mais
aussi mais
aussi  etc.
Entre autres, le cercle (G) coupe
l'axe Ox en deux points dont les abscisses sont etc.
Entre autres, le cercle (G) coupe
l'axe Ox en deux points dont les abscisses sont  et et
 . .
Si
le lecteur veut s'en assurer au moyen de
la figure, il pourra contrôler qu'en tout point de l'hyperbole,
les relations (entre autres):
 (20.91)
(20.91)
sont toujours vérifiées.
Si nous traçons maintenant sur un graphique:
 (20.92)
(20.92)
Nous
obtenons (ça c'est juste pour avoir vu une fois à quoi ressemblent
ces fonctions) avec Maple 4.00b:
>plot([sinh(x),cosh(x),tanh(x)],x=-2..2,color=[red,black,blue]);

Figure: 72.14 - Tracé des fonctions trigonométriques hyperboliques usuelles
Nous retrouverons la fonction cosh(x) dans
le chapitre de Génie Civil par exemple dans le cadre des
câbles
suspendus. Nous retrouverons aussi les fonctions sinh(x) et tanh(x)
dans le cadre de l'étude des vagues de gravité dans le chapitre
de Génie Marin Et Météo.
RELATIONS
REMARQUABLES
Soit par définition:
 (20.93)
(20.93)
et:  (20.94)
(20.94)
A
partir de ces définitions et à l'aide des opérations élémentaires
d'algèbre nous pouvons déterminer les relations
remarquables suivantes (c'est beaucoup plus facile que la détermination
de relations remarquables de la trigonométrie du cercle,
donc sauf demande nous donnons ces relations sans démonstration):
 (20.95)
(20.95)
Egalement:
 (20.96)
(20.96)
Et
nous avons les relations d'addition:
 (20.97)
(20.97)
Suite à la demande d'un étudiant, démontrons les
première et troisième
relations ci-dessus:
Pour la première:
 (20.98)
(20.98)
et la troisième:
 (20.99)
(20.99)
Signalons encore d'autres relations remarquables:
 (20.100)
(20.100)
et
encore:
 (20.101)
(20.101)
TRIGONOMÉTRIE
SPHÉRIQUE
L'objectif de la trigonométrie sphérique
est de déterminer les relations remarquables existantes
entre les angles et les côtés de formes projetées
(dites également "formes
géodésiques" car suivant la courbure
de l'espace) sur la surface d'une sphère. Pour déterminer
ces relations, nous allons nous intéresser
au cas particulier d'une sphère de rayon unité et
des relations entre les côtés d'un triangle (élément
de surface plane élémentaire)
et les différents angles existants. Nous verrons que les
résultats
sont au fait indépendants du rayon de la sphère et
de la forme considérée
initialement.
Soit la figure sur laquelle
se trouve un triangle géodésique de sommets A, B, C d'angles
d'ouverture respectifs  et
de côtés opposés a, b, c et
trois vecteurs et
de côtés opposés a, b, c et
trois vecteurs  unitaires
tels que unitaires
tels que  et
que l'extrémité de et
que l'extrémité de  soit
confondue avec le sommet A: soit
confondue avec le sommet A:

Figure: 72.15 - Construction pour introduire la trigonométrique sphérique
L'angle entre les points B et
C,
noté  ,
n'a pas pu être représenté sur le schéma ci-dessus faute de place. ,
n'a pas pu être représenté sur le schéma ci-dessus faute de place.
Rappelons que le périmètre d'un cercle
de rayon unité sur la sphère de rayon unité vaut bien évidemment
 .
Le périmètre du cercle en fonction de l'angle d'ouverture de ce
dernier étant donné par (relation très très souvent
utilisée
en physique!!!): .
Le périmètre du cercle en fonction de l'angle d'ouverture de ce
dernier étant donné par (relation très très souvent
utilisée
en physique!!!):
 (20.102)
(20.102)

Si le cercle est de rayon  (comme
c'est le cas pour notre sphère), le calcul de la longueur
d'arc se simplifie et devient: (comme
c'est le cas pour notre sphère), le calcul de la longueur
d'arc se simplifie et devient:
 (20.103)
(20.103)
Nous garderons cette contrainte du rayon unité pour la
suite afin de simplifier les expressions que nous allons obtenir
par la suite.
Conséquence relativement aux points
sur notre sphère; les côtés du triangle sont donnés
par:
 (20.104)
(20.104)
Considérons maintenant le
produit scalaire (cf. chapitre de Calcul
Vectoriel):
 (20.105)
(20.105)
et comme  (rayon
unité) nous
avons: (rayon
unité) nous
avons:
 (20.106)
(20.106)
Si nous décomposons les deux vecteurs
 et et
 sur
les vecteurs tangents unités nous avons: sur
les vecteurs tangents unités nous avons:
 (20.107)
(20.107)
Ce qui nous donne:
 (20.108)
(20.108)
ce qui donne (distributivité du produit
scalaire):

(20.109)
Comme  et et
 ,
la relation précédente se réduit à: ,
la relation précédente se réduit à:
 (20.110)
(20.110)
et comme:
 (20.111)
(20.111)
Nous avons:
 (20.112)
(20.112)
relation dite "relation
fondamentale"
ou "formule des cosinus" que
nous pouvons donc (de par le rayon unité) tout aussi bien écrire:
 (20.113)
(20.113)
Cette dernière
relation est invariante par permutation circulaire des variables
 .
Il est aussi intéressant de remarquer avant de continuer
que si le triangle sphérique est à angle droit en A,
la relation précédente se simplifie en: .
Il est aussi intéressant de remarquer avant de continuer
que si le triangle sphérique est à angle droit en A,
la relation précédente se simplifie en:
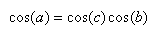 (20.114)
(20.114)
et si le triangle est suffisamment petit par rapport au rayon
et que nous faisons un développement de Taylor (cf.
chapitre Suites et Séries) proche de
0 au deuxième
ordre pour chacun des termes il
vient:
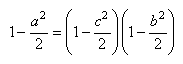 (20.115)
(20.115)
soit:
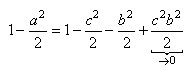 (20.116)
(20.116)
après simplification:
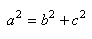 (20.117)
(20.117)
nous retrouvons le théorème de Pythagore (cf.
chapitre de Géométrie Euclidienne). Donc:
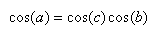 (20.118)
(20.118)
est le pendant en géométrie sphérique
(géométrie
non-euclidienne) du théorème de Pythagore de la géométrie
plane (géométrie euclidienne).
Cette paranthèse fermée, revenons en à nos
moutons. Les sinus de tous les angles étant
positifs (puisque inférieurs à  ),
nous pouvons écrire: ),
nous pouvons écrire:
 (20.119)
(20.119)
Cette dernière
relation est bien évidemment également invariante
par permutation circulaire des variables  .
Donc nous obtenons une relation remarquable du triangle sphérique,
appelée "relation des sinus" ou
"formule des sinus": .
Donc nous obtenons une relation remarquable du triangle sphérique,
appelée "relation des sinus" ou
"formule des sinus":
 (20.120)
(20.120)
Comme la
trigonométrie sphérique est souvent utilisée pour des repérages
terrestres, avec souvent 2 cercles très particuliers et orthogonaux: l'équateur terrestre et un méridien ou un parallèle quelconque,
ce cas revêt un intérêt particulier. Dans
le cas d'un triangle rectangle en A nous
avons bien évidemment:
 (20.121)
(20.121)
Toutes les
relations que nous avons déterminées jusqu'à maintenant
nous permettent dans le cas où  et et
 de
tirer des relations très intéressantes pour la
géophysique: de
tirer des relations très intéressantes pour la
géophysique:
 (20.122)
(20.122)
Évidemment,
nous n'avons pas présenté ici toutes les relations de trigonométrie
sphérique existantes, mais au moins les plus importantes qu'il
faut savoir retrouver.
Remarque: Nous définissons " l'excédent"
ou " excès sphérique" par
le nombre:
 (20.123)
(20.123)
Pendant que nous y sommes, profitons-en
pour calculer un problème classique qui est celui de la
surface d'un triangle sur une sphère. Soit la figure:

Figure: 72.16 - Construction pour l'étude des angles d'un triangle sphérique
Si
nous prolongeons les arcs de géodésique AC et
AB jusqu'à
 , nous
obtenons une tranche
de sphère dont la surface , nous
obtenons une tranche
de sphère dont la surface  est
proportionnelle à l'angle est
proportionnelle à l'angle  ,en
A.
Si cet angle valait ,en
A.
Si cet angle valait  ,
nous aurions toute la sphère et la surface vaudrait ,
nous aurions toute la sphère et la surface vaudrait  .
Comme l'angle vaut .
Comme l'angle vaut  ,
la proportionnalité nous dit que ,
la proportionnalité nous dit que  vaut: vaut:
 (20.124)
(20.124)
De
la même manière, si nous prolongeons les arcs BC et
BA jusqu'à
 et
si nous prolongeons les arcs CA et
CB jusqu'à et
si nous prolongeons les arcs CA et
CB jusqu'à
 ,
nous obtenons deux autres tranches dont les surfaces ,
nous obtenons deux autres tranches dont les surfaces  et et
 valent: valent:
 (20.125)
(20.125)
Supposons
maintenant que nous additionnions ces trois surfaces:
 (20.126)
(20.126)
nous
obtenons alors la moitié de la sphère  (regarder
la figure pour vous le représenter mentalement) plus
2 fois le triangle géodésique
de surface S en rose sur la figure (car pris en compte
2 fois en trop). (regarder
la figure pour vous le représenter mentalement) plus
2 fois le triangle géodésique
de surface S en rose sur la figure (car pris en compte
2 fois en trop).
Il faut enlever deux fois la surface de ce triangle bleu pour
obtenir la surface de la demi-sphère:
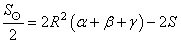 (20.127)
(20.127)
Donc:
 (20.128)
(20.128)
comme
 ,
nous avons: ,
nous avons:
 (20.129)
(20.129)
Après
simplification nous en déduisons que la surface S du
triangle ABC vaut::
 (20.130)
(20.130)
où  est
un angle solide. est
un angle solide.
Il
est assez simple de généraliser ce concept à d'autres formes du
même acabit (en particulier celles composées de triangles...).
ANGLE SOLIDE
En géométrie spatiale, se pose le problème
du concept d'angle d'ouverture d'une portion de l'espace (en extension à l'angle
dit "angle plan"). Nous définissons
alors "l'angle solide"  par la mesure de la portion d'espace limitée par une surface
conique de sommet O et
nous l'exprimons en stéradian, obtenue par le rapport:
par la mesure de la portion d'espace limitée par une surface
conique de sommet O et
nous l'exprimons en stéradian, obtenue par le rapport:
 (20.131)
(20.131)
S
étant l'aire de la calotte découpée par le cône sur une sphère de
rayon r.

Figure: 72.17 - Configuration pour la définition de l'angle solide
Si  est
le demi-angle du cône, nous obtenons pour ce rapport (pour le calcul
de la calotte d'une surface sphérique voir le chapitre traitant
des formes géométriques): est
le demi-angle du cône, nous obtenons pour ce rapport (pour le calcul
de la calotte d'une surface sphérique voir le chapitre traitant
des formes géométriques):
 (20.132)
(20.132)
D'où l'on conclut que l'angle solide
total vaut par définition:
 (20.133)
(20.133)
Nous pouvons également calculer
"l'angle solide élémentaire" tel que représenté ci-dessous:

Figure: 72.18 - Configuration pour la définition de l'angle solide élémentaire
Soit un
angle solide élémentaire
 et
OM l'axe
du cône. Nous posons: et
OM l'axe
du cône. Nous posons:
 (20.134)
(20.134)
Nous considérons une surface quelconque
 passant
par le point M. passant
par le point M.
 découpe sur cette surface une portion
découpe sur cette surface une portion  . .
Si nous
traçons la sphère S de
centre O et
de rayon r,
cet angle solide découpe sur cette sphère une calotte d'aire dS:
 (20.135)
(20.135)
Soit MN la
normale à  qui fait un angle
qui fait un angle  avec
OM.
Nous avons, en assimilant dS et avec
OM.
Nous avons, en assimilant dS et
 à
des portions de plan: à
des portions de plan:
 (20.136)
(20.136)
d'où:
 (20.137)
(20.137)
Ce concept
d'angle solide nous sera très utile en particulier dans
le domaine de la physique théorique qui traite du rayonnement
thermique (cf. chapitres d'Optique et de
Thermodynamique).
Nous pouvons encore calculer à partir
des concepts précédents, l'angle solide élémentaire
de révolution tel que présenté sur la figure ci-dessous:

Figure: 72.19 -Configuratio pour la définition de l'angle solide élémentaire
de
révolution
Il est compris entre deux
angles solides de révolution dont les demi-angles au sommet
diffèrent
de  : :
 (20.138)
(20.138)
où:
 (20.139)
(20.139)
Démonstration:
Dans le chapitre traitant des Formes Géométriques (cf.
section de Géométrie) nous avons démontré les
différentes
manières de calculer la surface d'une sphère. De ces calculs il
avait été déduit que la surface élémentaire à R constant
était:
 (20.140)
(20.140)
et puisque:
 (20.141)
(20.141)
l'angle
solide élémentaire s'écrit alors:
 (20.142)
(20.142)
Ainsi,
l'angle solide délimité par un cône de révolution, d'angle au
somment  vaut: vaut:
 (20.143)
(20.143)
 C.Q.F.D. C.Q.F.D.
|