|

GÉNIE MARIN & MÉTÉO | GÉNIE
MÉCANIQUE | GÉNIE ÉLECTRIQUE
GÉNIE ÉNERGÉTIQUE | GÉNIE
CIVIL | GÉNIE BIOLOGIQUE | GÉNIE
AÉROSPATIAL
GÉNIE CHIMIQUE | GÉNIE INDUSTRIEL |
GÉNIE LOGICIEL
Dernière mise à jour de ce chapitre:
2017-01-31 10:13:32 | {oUUID 1.780}
Version: 3.0 Révision 7 | Avancement:
~20%
 vues
depuis
le 2012-01-01:
10'424 vues
depuis
le 2012-01-01:
10'424
 LISTE DES SUJETS TRAITÉS SUR CETTE PAGE
LISTE DES SUJETS TRAITÉS SUR CETTE PAGE
Le Génie Mécanique
désigne l'ensemble des connaissances
liées à la mécanique, au sens physique (sciences des mouvements)
et au sens technique (étude des mécanismes). Ce champ de connaissances
va de la conception d'un produit mécanique
au recyclage de ce dernier en passant, bien sûr par la fabrication,
la maintenance, etc.
Ses applications sont très importantes dans de nombreux domaines
de la vie de tous les jours que ce soit pour la fabrication de
machines, de jouets, d'appareils électro-ménagers
ou encore d'immeubles ou de toutes sortes de moyens de transports...
et la liste est
encore longue...
Encore une fois, nous allons nous concentrer ici uniquement sur la formalisation
mathématique de cas pratiques d'applications courantes! Donc ce chapitre
est seulement une introduction générale des applications techniques
de la mécanique et doit être complété par des
travaux pratiques en laboratoire ainsi que par la lecture du chapitre de
Thermodynamique où l'équation d'état des solides y est
traitée.
Remarque: Il serait prétentieux de prétendre
dans le présent chapitre
vouloir faire aussi bien et complet que les PDF gratuits d'Éléments
de machine et de Résistance des Matériaux de
Nicolet Gaston
Raymond qui sont
inégalables
en
matière de
contenu et de qualité à ce jour (même comparés
aux ouvrages payants sur le sujet!). Il est donc fortement recommandé au
lecteur de s'y référer s'il veut une information complète
sur le génie mécanique (voir la section de téléchargement du
site).
ENGRENAGES
Un engrenage est un système mécanique composé de deux roues dentées engrenées
servant à la transmission du mouvement de rotation entre elles ou à la
propulsion d'un fluide (nous parlons alors de pompe à engrenages):

Figure: 70.1 - Système d'engrenage à deux roues dentées circulaires
L'inventeur de la roue dentée est non moins que le célèbre mathématicien,
ingénieur et physicien Archimède.
Nous trouvons les engrenages absolument partout dans notre quotidien:
voitures, vélos, montres, chaises réglables, etc. Nous conseillons par ailleurs
vivement au lecteur de penser aux engrenages (plateaux et pignons liés par
une chaîne de transmission) de son vélo pour interpréter les
résultats
qui vont suivre.
Il m'a semblé donc important de présenter très brièvement comment calculer
le pas de denture d'une roue cylindrique en fonction d'une autre pour le
plus connu des engrenages qui est "l'engrenage
cylindrique" comme
celui représenté ci-dessous:

Figure: 70.2 - Engrenage cylindrique avec grammaire
Pour assurer l'entraînement, nous devons donc faire en sorte
que les dents d'une des roues cylindriques de diamètre 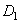 s'intercalent
bien entre les dents d'une autre roue de diamètre s'intercalent
bien entre les dents d'une autre roue de diamètre 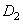 .
Pour cela, il nous faut introduire la notion de "pas" de
la denture de chaque roue que nous noterons respectivement .
Pour cela, il nous faut introduire la notion de "pas" de
la denture de chaque roue que nous noterons respectivement 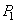 et et 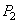 . .
Pour cela nous allons utiliser l'hypothèse que le point de friction des
dents est assimilable aux diamètres (représentés ci-dessous par des cercles
noirs) qu'auraient les roues cylindriques s'il n'y avait pas de glissement
(et donc pas besoin de dents...) de la même façon que l'engrenage. Ces cercles
sont appelés "cercles primitifs", ou "cylindres
primitifs" ou
encore "diamètres primitifs".
Le pas des dents va s'exprimer donc en fonction de la circonférence et
du nombre de dents sur chaque roue. Si nous notons 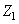 le
nombre de dents d'une roue cylindrique 1 et le
nombre de dents d'une roue cylindrique 1 et 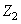 le
nombre de dents d'une roue cylindrique 2, nous avons alors les pas qui valent
respectivement: le
nombre de dents d'une roue cylindrique 2, nous avons alors les pas qui valent
respectivement:
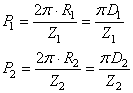 (70.1)
(70.1)
et comme pour que l'engrenage fonctionne il faut que les deux pas soient égaux:
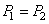 (70.2)
(70.2)
Nous obtenons alors:
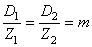 (70.3)
(70.3)
où m est appelé le "module de
denture".
Nous retiendrons donc que:
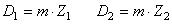 (70.4)
(70.4)
Nous observons aussi de par les relations ci-dessus que le pas est donc
proportionnel au module de denture (le choix d'un gros module donne un nombre
de dents faible et le choix d'un petit module un grand nombre de dents).
Le choix du module d'un engrenage s'effectue (parmi des valeurs normalisées) à partir
de critères de résistance à la rupture ou de résistance à l'usure.
RAPPORTS DE TRANSMISSION
Le "rapport de transmission" appelé aussi "rapport
de réduction" d'un
engrenage ou d'un système de poulies très important dans le domaine
de la mécanique et est défini
par:
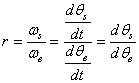 (70.5)
(70.5)
et donc si la vitesse de rotation (pulsation) est constante (voir le chapitre
de Mécanique Classique pour les calculs détaillés de la cinématique du mouvement
circulaire) et ne varie plus entre le démarrage
et le fonctionnement nominal, il vient:
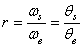 (70.6)
(70.6)
Il s'agit d'une technique très utilisée dans les voitures
(en général presque dans tous les moteurs):

Figure: 70.3 - Moteur avec quelques poulies et courroies de transmission
aussi bien que dans presque toutes les montres mécaniques:

Figure: 70.4 - Système d'engrenage avec rapport de transmission particulier
d'une montre
Nous avons aussi bien évidemment:
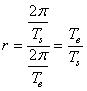 (70.7)
(70.7)
Donc, le rapport des vitesses de rotation (pulsation) entre l'arbre de
sortie et l'arbre d'entrée est égal au rapport des angles parcourus entre
l'arbre de sortie et l'arbre d'entrée.
Nous avons de même:
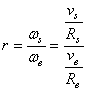 (70.8)
(70.8)
et comme au point de contact il y a frottement sans glissement alors les
deux vitesses sont égales et donc au final:
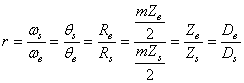 (70.9)
(70.9)
L'égalité:
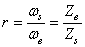 (70.10)
(70.10)
est souvent appelée aussi "rapport de réduction". Il est bien évidemment
important de considérer un rapport de réduction sous forme fractionnaire
comme une chose qui existe. Ainsi, pour un r donné il faut chercher
la fraction la plus proche.
Il paraît clair que si l'engrenage est réducteur de vitesse alors:
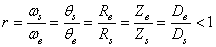 (70.11)
(70.11)
Raison pour laquelle en vélo, lorsque nous sommes en descente et que la
roue motrice tourne très rapidement, nous allons favoriser un grand plateau
et un petit pignon (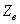 très
grand par rapport à très
grand par rapport à 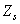 ).
Ainsi, avec à 60 [km/h] en descente, une roue de vélo de cours de
rayon d'environ 35 [mm] aura une vitesse de rotation: ).
Ainsi, avec à 60 [km/h] en descente, une roue de vélo de cours de
rayon d'environ 35 [mm] aura une vitesse de rotation:
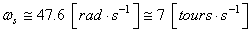 (70.12)
(70.12)
or il n'est pas concevable de tourner les jambes aussi vite pour aller
encore plus vite... Donc avec un rapport plateaux/pignons de 53/12, nous
aurons:
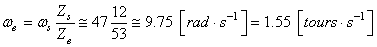 (70.13)
(70.13)
ce qui est déjà beaucoup plus acceptable... pour aller encore plus vite.
Maintenant observons ce qui se passe au niveau du moment de force (qu'il
est dur par exemple en vélo de grimper une côte avec un grand plateau et
un petit pignon et nous allons voir pourquoi il vaut mieux favoriser un petit
plateau avec un grand pignon).
Revenons sur notre schéma en représentant un moment de force constant dont
le module 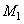 est
appliqué sur un pignon à l'engrenage d'entrée de rayon est
appliqué sur un pignon à l'engrenage d'entrée de rayon 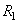 selon
(cf. chapitre de Mécanique Classique): selon
(cf. chapitre de Mécanique Classique):
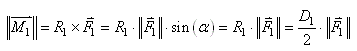 (70.14)
(70.14)
La force 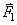 tangentielle
sur l'engrenage d'entrée est la même que celle qui fait tourner l'engrenage
de sortie tangentielle
sur l'engrenage d'entrée est la même que celle qui fait tourner l'engrenage
de sortie

Figure: 70.5 - Engrenage cylindrique avec forces sur pont de contact
Nous avons alors pour les deux engrenages, en l'absence de force de frottement
et en considérant que la force au point de contact des deux engrenages est
perpendiculaire aux deux rayons respectifs, les relations suivantes :
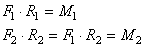 (70.15)
(70.15)
Nous égalisons alors:
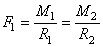 (70.16)
(70.16)
et donc:
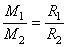 (70.17)
(70.17)
et donc:
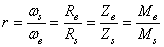 (70.18)
(70.18)
Ainsi, pour reprendre notre exemple du vélo... si nous souhaitons appliquer
le plus grand moment de force possible à la roue arrière en minimisant le
moment de force que nous fournissons sur le pédalier alors la meilleure stratégie
selon la relation déterminée ci-dessus est de mettre le plus petit plateau
possible associé au plus grand pignon (l'idéal serait d'avoir un plateau
plus petit que le plus grand des pignons pour avoir un rapport de transmission
supérieur à l'unité).
Attention! Le principe des poulies/engrenages avec rapport de transmission
est un fantastique démultiplicateur de force mais en aucun cas il
démultiplie
le travail!
Remarque: La norme ISO 1122-1 donne la définition
inverse et note le rapport de transmission i au lieu de r:
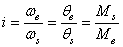 (70.19)
(70.19)
ASSOCIATION D'ENGRENAGES
Pour des raisons de contraintes géométriques ou mécaniques, il est parfois
nécessaire de construire des étages d'engrenages comme le montre par exemple
le train de rouage à 4 roues de la figure ci-dessous (nous allons voir un
exemple une fois les notions de base introduites):

Figure: 70.6 - Exemple de train d'engrenage en 3D
Soit sous forme schématique technique (non conforme aux normes VSM Suisses
mais pratique):

Figure: 70.7 - Train d'engrenage 2D équivalant
Le rapport de transmission global sera alors donné pour la vitesse de rotation
par:
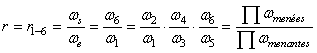 (70.20)
(70.20)
où la quatrième égalité se simplifie parce que dans
le cas particulier ci-dessus:
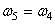 et et 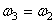 (70.21)
(70.21)
Nous pouvons aussi exprimer la transmission totale en termes de diamètres.
Puisque nous avons démontré que:
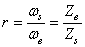 (70.22)
(70.22)
il vient alors immédiatement:
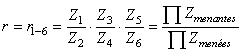 (70.23)
(70.23)
expression que nous ne pouvons pas simplifier!
Ainsi, dans le cadre d'une transmission d'une montre à complication astronomique,
le rapport de transmission a été obtenu en déterminant la fraction rationnelle
1802/217. Cela étant très difficile à mettre en oeuvre avec uniquement deux
engrenages, nous allons construire simplement à l'aide de trois axes et quatre
roues (à 7, 31, 34 et 53 dents) le même rapport qui heureusement n'est
pas irréductible - de la façon suivante:
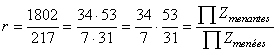 (70.24)
(70.24)
 Exemple: Exemple:
Nous souhaitons avec un train à 4 roues sur 2 axes, entraîné par l'axe
des heures (qui fera un tour en 12 heures), réaliser un rapport r de
transmission très précis, pour réaliser l'entraînement d'une complication
de montre incluant une phase de lune par le classique disque portant 2 lunes
et tournant derrière
un masque.
Le nombre maximum de dents par roue ne devra pas excéder 300 dents et ne
descendra pas en dessous de 7. La précision sera la meilleure permise dans
les limites de ces nombres de dents.
Nous prendrons pour la lunaison 29 jours 12 heures 44 minutes et 2.9 secondes,
soit 2'551'442.9 secondes.
Le calcul du rapport recherché est relativement simple. Le disque à deux
lunes fait un tour complet en 2 lunaisons, soit en 5'102'885.8 secondes.
La roue du garde-temps fait un tour en 12 heures, soit 43'200 secondes.
Pour un tour du disque à 2 lunes (axe mené) l'axe de la roue 12h (axe menant)
fait :
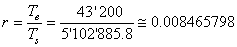 (70.25)
(70.25)
et en arrondissant comme ci-dessous, nous avons une erreur d'environ 3
dix-millième de seconde par tranche de 12 heures. Soit environ 0.2 secondes
par année de retard. Ce qui est acceptable pour une montre mécanique.
En arrondissant à:
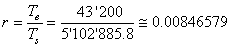 (70.26)
(70.26)
nous avons une erreur d'environ 30 secondes par année ce qui reste toujours
acceptable pour une montre mécanique. Si nous enlevons encore une décimale,
nous avons alors un retard de 6 minutes par année, en enlevant encore une
décimale supplémentaire, nous aurions un retard de 49 minutes (ce qui reste
toujours acceptable pour nombre de montres mécaniques). Par contre au-delà ce
n'est plus acceptable!
Maintenant, pour trouver la fraction rationnelle décomposable la plus proche
de ce chiffre il existe de nombreuses méthodes empiriques (par tâtonnement
ou en utilisant un arbre de Brocot) et des tables mais la moins pire... pour
moi... est celle utilisant les fractions continues (cf.
chapitre de Théorie
des Nombres) quand elle est applicable...
Rappelons que nous avons vu démontré que:
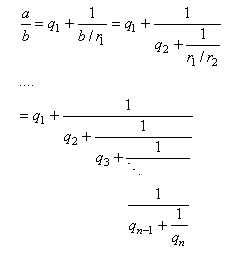 (70.27)
(70.27)
en considérant:
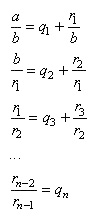 (70.28)
(70.28)
Si nous notons x le rapport a/b alors les relations
ci-dessous nous donnent que 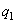 est
la partie entière de x, est
la partie entière de x, 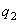 la
partie entière de la
partie entière de 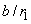 soit
de soit
de 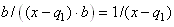 et
ainsi de suite et
ainsi de suite
Nous avons alors dans notre cas:
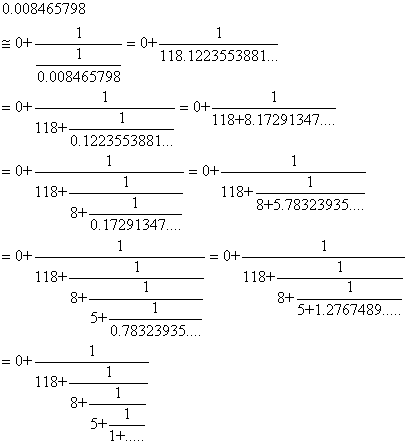 (70.29)
(70.29)
Soit après une mise au dénominateur commun:
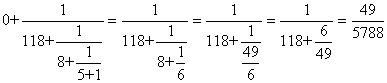 (70.30)
(70.30)
Si la différence (erreur) entre cette fraction et la valeur exacte est
acceptable (il suffit de calculer l'erreur de temps que cela provoque après
une année de fonctionnement de la montre par exemple), nous nous arrêtons
ici. Mais il y a un deuxième critère... le numérateur et le dénominateur
doivent être décomposables de manière satisfaisante relativement aux exigences
du nombre de dents. Or dans le cas présent, le dénominateur (5788) n'est
pas décomposable de manière satisfaisante par rapport à nos contraintes (faites
la décomposition avec la commande ifactor de Maple 4.00b et vous verrez!).
Si nous continuons à développer notre fraction continue, nous ne trouverons
pas de solution acceptable avant que le numérateur ou le dénominateur dépasse
la valeur maximale admise de 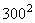 . .
Dès lors, nous revenons par exemple à la fraction (bon ce n'est pas une
approximation acceptable car dans la réalité le déréglage de la montre se
fera trop vite):
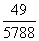 (70.31)
(70.31)
et nous trichons un peu par essais successifs jusqu'à trouver un bon rapport:
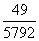 (70.32)
(70.32)
Ensuite, comme nous avons un train à quatre roues, nous devons avoir:
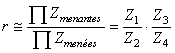 (70.33)
(70.33)
et nous prenons alors (toujours en nous aidant de la commande ifactor
de Maple 4.00b):
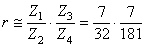 (70.34)
(70.34)
RÉSISTANCE DES
MATÉRIAUX (R.D.M.)
La résistance des matériaux (R.D.M. se dit "ResDem"
pour les intimes...) est, comme tous les autres chapitres de
ce site, un domaine extrêmement
vaste dont le niveau de détail et la complexité des
calculs peut exploser. Nous allons dans les paragraphes qui suivent
nous attarder
sur l'essentiel que l'ingénieur (en entreprise) doit savoir.
Les développements sont simplifiés à l'extrême
pour des cas particuliers triviaux (barres et poutres rectilignes).
Dans la réalité,
il faut utiliser le calcul tensoriel, les plans d'expérience
ou la modélisation informatique avec les
MEF (méthodes des éléments finis).
Avant de commencer à étudier quelques cas concrets simples
faisons quelques rappels des démonstrations issues du chapitre
de Mécanique des Milieux Continus:
Le solide considéré comme rigide n'existe pas, ce n'est qu'une
approximation commode. L'expérience montre en effet qu'un solide
est toujours légèrement déformable sous l'effet de forces extérieures.
Les relations entre déformations et tensions sont en général
compliquées par suite de l'anisotropie des réseaux cristallins.
Cependant, les solides n'étant généralement pas des monocristaux
mais des substances polycristallines, constituées d'assemblages
de microcristaux associés au hasard, ils peuvent être considérés
comme isotropes.
Ensuite, il convient de considérer globalement les hypothèses
suivantes relativement aux développements qui vont suivre:
H1. La matière est homogène, c'est-à-dire pour rappel de même
constitution physique et de même structure dans tout le volume
de la pièce.
H2. La matière est isotrope, c'est-à-dire pour rappel que ses
propriétés mécaniques sont les mêmes en tout point du corps.
H3. La matière est parfaitement élastique, c'est-à-dire
pour rappel qu'après élimination des efforts extérieurs,
la pièce
reprend immédiatement ses dimensions primitives (au contraire
de la limite plastique!).
H4. Les déformations (déplacements des points
de la ligne caractéristiques)
sont petites par rapport aux dimensions des objets étudiés.
H5. Toute section droite (sections transversales) avant déformation
reste droite après
déformation (hypothèses de Navier-Bernoulli).
H6. Les résultats obtenus en R.D.M. ne s'appliquent valablement
qu'à une distance suffisamment éloignée
de la région d'application
des efforts concentrés (Hypothèse de Barré de
Saint Venant).
H7. Dans le domaine élastique, la matière obéit à la
loi de proportionnalité et dons les déformations
sont liées par la loi
de Hooke démontrée dans le chapitre de Mécanique
Des Milieux Continus. Cette loi linéaire permet d'appliquer
le principe de superposition des forces et des déformations à la
résistance.
Nous avons vus dans le chapitre de Mécanique des Milieux
Continus que la loi de Hooke stipule, lorsque les déformations
sont réversibles, qu'il y a proportionnalité entre
tension et déformation
(une des variantes de formulation de la loi de Hooke):
 (70.35)
(70.35)
ou:
 (70.36)
(70.36)
où E est le module de Young,  la
déformation normale et la
déformation normale et  la
contrainte normale. Indiquons que le rapport: la
contrainte normale. Indiquons que le rapport:
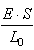 (70.37)
(70.37)
est souvent appelée "raideur
de la barre" dans la littérature
spécialisée et est souvent notée k.
Nous avons également démontré dans le chapitre de Mécanique
des Milieux Continus que la contrainte tangentielle était donnée
par:
 (70.38)
(70.38)
où G est le module de cisaillement,  est
l'angle de déformation et est
l'angle de déformation et  le
coefficient de Poisson, nombre sans dimensions. Nous avons donc
une relation entre le module d'élasticité et de rigidité valable
dans le cas des petites déformations. le
coefficient de Poisson, nombre sans dimensions. Nous avons donc
une relation entre le module d'élasticité et de rigidité valable
dans le cas des petites déformations.
Nous avons vu également dans le même chapitre que pour un solide
ou un liquide soumis à une surpression isotrope uniforme
nous avions:
 (70.39)
(70.39)
Le coefficient de compressibilité  est
donc un nombre positif, par conséquent en utilisant la relation
précédente, nous avons: est
donc un nombre positif, par conséquent en utilisant la relation
précédente, nous avons:
 (70.40)
(70.40)
et vient alors un résultat connu:
 (70.41)
(70.41)
Donc le coefficient de Poisson ne peut pas être plus grand
que ½ et il peut être négatif (dans ce dernier cas nous parlons
alors de matériaux
auxétiques).
Enfin, rappelons que nous avons vu dans le chapitre de Mécanique
des Milieux Continus que la contraction unitaire selon l'axe z était
donnée lors d'une traction selon l'axe x par:
 (70.42)
(70.42)
Soit autrement écrit (en se concentrant sur le plan XZ):
 (70.43)
(70.43)
Soit:
 (70.44) (70.44) Et c'est ce que montre la figure ci-dessous:

Figure: 70.8 - Traction sur une pièce test
Nous avons également démontré dans le chapitre
de Mécanique
des Milieux Continus la relation suivante lors de notre étude
du module de flexion:
 (70.45)
(70.45)
qui exprime le moment de flexion pour une poutre sous un effort
M (moment de force), la travée d'écrivant
alors un arc de cercle de rayon de courbure R et où I caractérise
la "rigidité de
forme" du matériau
ayant une aire transversale donnée.
C'est une relation très importante dans de nombreux domaines
de la construction (navale, automobile, architecture, etc.).
Remarque: I est
appelé le "moment
d'inertie statique" ou "moment
quadratique" comme nous l'avons déjà spécifié dans
le chapitre de mécanique des milieux continus.
MOMENTS QUADRATIQUES
Voyons les trois moments d'inerties statiques  classiques
du domaine de la RDM car souvent rencontrés dans la pratique
(construction). classiques
du domaine de la RDM car souvent rencontrés dans la pratique
(construction).
Remarque: La théorie des
moments d'inertie est pour rappel présentée dans
le chapitre de Mécanique Classique. Dans le chapitre
sur les Formes Géométriques nous avions démontré en
détails les moments d'inerties
des volumes les plus courants.
1. Moment d'inertie statique transversal de la plaque rectangulaire
de côté b et hauteur h:

Figure: 70.9 - Plaque rectangulaire et axe d'inertie
Le domaine occupé par la plaque est donné par:
 (70.46)
(70.46)
Nous avons alors:
 (70.47)
(70.47)
2. Moment d'inertie statique transversal d'un disque de diamètre:

Figure: 70.10 - Disque et axe d'inertie
Ici le domaine d'intégration est:
 (70.48)
(70.48)
où d est le diamètre du disque.
Nous avons toujours:
 (70.49)
(70.49)
Pour calculer cette intégrale, nous utilisons les coordonnées
polaires:
 (70.50)
(70.50)
Le jacobien de la transformation est égal à r (cf.
chapitre de Calcul Différentiel Et Intégral). Nous obtenons:
 (70.51)
(70.51)
3. Moment d'inertie statique d'une couronne de diamètre
extérieur D et
diamètre intérieur d:

Figure: 70.11 - Couronne et axe d'inertie
Ici le domaine d'intégration est:
 (70.52)
(70.52)
où D et d sont respectivement les diamètres du
grand et du petit disque.
Si nous notons  le
domaine du grand disque et le
domaine du grand disque et  celui
du petit disque alors: celui
du petit disque alors:
 (70.53)
(70.53)
en utilisant le moment d'inertie statique du disque.
Pour résumer, nous avons donc:
 (70.54)
(70.54)
et enfin il existe aussi le moment quadratique polaire de S par
rapport à un point O:
 (70.55)
(70.55)
Il est donc aisé dans des cas simples de connaître le
moment d'inertie polaire et celui-ci est très utile dans
le cadre de l'étude de la torsion.
Il découle de ces outils que plus les éléments de la section
sont situés loin de l'axe, plus le moment quadratique sera important
et plus (nous le démonterons dans ce qui suit) les flèches seront
faibles.
ÉQUATION DE LA LIGNE ÉLASTIQUE
Pour cet exemple de cas d'école mais très utilisé dans la pratique
nous allons d'abord devoir obtenir mathématiquement la forme
géométrique que prend la fibre neutre d'une poutre soumise à des
efforts de flexion.
Remarque: Si toutes
les réactions d'un système sollicité se
trouvent à partir des
équations d'équilibre statique, le problème
est dit "statiquement
déterminé" ou "isostatique".
Lorsque les équations de la statique ne permettent pas
de trouver l'équilibre d'un système, le système
est dit "hyperstatique"
ou "statiquement indéterminé".
Nous disons aussi que tant qu'il y a une "liberté de
mouvement" malgré n points de liaison,
nous sommes en isostatique.
En faisant l'hypothèse que les déformations sont faibles et
que le poids de la poutre est faible devant la force qui plie
la poutre, nous pouvons faire le schéma suivant:

Figure: 70.12 - Poutre (simplifiée...) soumise à un effort
Par définition de la dérivée et en vertu de l'hypothèse des
faibles déformations (cela fonctionne donc quand même bien jusqu'à 45°...):
 (70.56)
(70.56)
Soit en dérivant encore une fois:
 (70.57)
(70.57)
D'autre part, la figure montre que (cf.
chapitre de Trigonométrie):
 (70.58)
(70.58)
Mais du fait que la courbe de la fibre neutre s'écarte
peu de l'axe y (déformations faibles), nous pouvons écrire:
 (70.59)
(70.59)
Donc:
 (70.60)
(70.60)
Ainsi, nous pouvons écrire en utilisant les relations
obtenues plus haut:
 (70.61)
(70.61)
qui est donc l'équation différentielle donnant  ,
appelée "équation de
la ligne élastique". ,
appelée "équation de
la ligne élastique".
Une autre approche courante mais moins intuitive pour obtenir
la même
relation est de partir de:
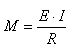 (70.62)
(70.62)
et de rappeler que le rayon de courbure R est
donné par (cf. chapitre de Géométrie
Différentielle):
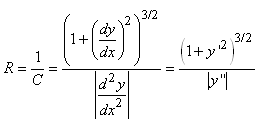 (25.63)
(25.63)
Soit en adaptant l'écriture à notre contexte:
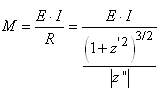 (25.64)
(25.64)
et en négligeant la dérivée
première pour les faibles
déformations nous retrouvons bien:
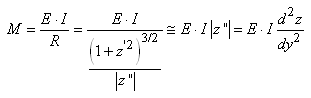 (25.65)
(25.65)
 Exemples: Exemples:
E1. Poutre encastrée que d'un seul côté dite
"poutre en porte à faux" (cas classique dans
la construction et les habitations) avec charge concentrée
(ponctuelle) à l'extrémité:

Figure: 70.13 - Poutre encastrée d'un seul côté avec force ponctuelle
Dans la section S quelconque, le moment de force (de
flexion) vaut donc:
 (70.66)
(70.66)
D'autre part:
 (70.67)
(70.67)
En éliminant R entre ces deux relations, il reste:
 (70.68)
(70.68)
La figure montre que les conditions aux limites sont:
 (70.69)
(70.69)
Nous tirons après intégration:
 (70.70)
(70.70)
Soit:
 (70.71)
(70.71)
Si  la
déformation est maximale et z prend donc la valeur maximale f appelée
la "flèche". Il s'ensuit: la
déformation est maximale et z prend donc la valeur maximale f appelée
la "flèche". Il s'ensuit:
 (70.72)
(70.72)
Soit la déformation verticale maximale de
l'extrémité pour
une poutre encastrée que d'un côté est finalement:
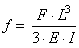 (70.73)
(70.73)
Toutes les données de cette relation nous sont connues
(force, longueur, module de Young, inertie statique) et il est
alors possible de déterminer
si la barre va casser ou non car il suffit d'appliquer la relation
démontrée
plus haut:
 (70.74)
(70.74)
Et donc grâce à la relation:
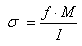 (70.75)
(70.75)
et sachant expérimentalement à partir de quelle
valeur expérimentale de  le
matériau casse on saura quand la barre cassera (du
moins approximativement!) en connaissant la flèche f,
le moment fléchissant M et le moment quadratique I. le
matériau casse on saura quand la barre cassera (du
moins approximativement!) en connaissant la flèche f,
le moment fléchissant M et le moment quadratique I.
Nous avons donc un résultat qui va nous être utile par la suite:
 (70.76)
(70.76)
et en intégrant de 0 à L nous retrouvons la flèche de
notre poutre précédente!
E2. La poutre soutenue (appelée aussi "poutre à 2
appuis simples" ou "poutre isostatique")
est l'exemple le plus classique en construction et donc en architecture
(et
ceux
qui
ont joué pendant
l'enfance
à mettre des lattes de bois pour passer par dessus une
petite rivière). Il s'agit d'une poutre homogène,
de section constante, reposant sur deux appuis libres à ses
extrémités
et soumis à une charge F en son centre:

Figure: 70.14 - Poutre soutenue avec force ponctuelle centrée
Nous pouvons donc considérer que tout se passe comme
si nous avions F/2 aux deux extrémités de
deux poutres de longueur L/2 (ainsi la somme vaut bien
F, c'est-à-dire le moment fléchissant).
Remarquons que nous négligeons
le poids de la poutre devant F,
mais F peut être tout simplement le poids de la poutre!
En utilisant la dernière relation de l'exemple précédent,
nous avons:
 (70.77)
(70.77)
Soit:
 (70.78)
(70.78)
Soit la déformation verticale maximale d'une poutre
posé des
deux côtés est finalement (en changeant un peu la
notation):
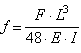 (70.79)
(70.79)
Ainsi, pour une même longueur de poutre, à F identique
la flèche est donc 16 fois moindre que pour une poutre
encastrée! Il était intuitif qu'elle soit moins élevée
pour une force identique mais difficile de deviner qu'elle le
serait d'un facteur 16!
C'est cette relation qui est aussi utilisée pour les poutres
IPN (fameuses en construction!).
E3. Poutre encastrée que d'un seul côté dite "poutre
en porte à faux" (cas classique dans la construction
et les habitations) avec charge linéique constante w:

Figure: 70.15 - Poutre encastrée d'un seul côté avec force linéique
constante
Le développement est simple mais certaines simplifications
sont astucieuses afin d'obtenir un résultat élégant.
Nous partons toujours de l'équation
de la ligne élastique
en adoptant les écritures à la configuration choisie: 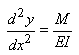 (70.80)
(70.80)
Soit explicitement:
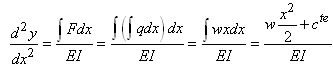 (70.81)
(70.81)
Comme le moment de force M est nul en x =
0, nous avons la constante qui est nulle. Dès lors:
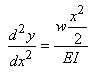 (70.82)
(70.82)
En intégrant encore une fois, il vient:
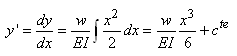 (70.83)
(70.83)
Comme pour x = L par hypothèse
la déformation est
nulle, nous avons la constante qui est alors donnée par:
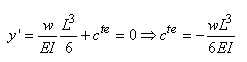 (70.84)
(70.84)
Soit:
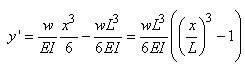 (70.85)
(70.85)
En intégrant encore une dernière fois:
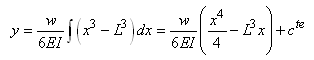 (70.86)
(70.86)
Et comme en x = L nous avons y qui
est aussi nul, il vient pour la constante:
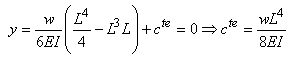 (70.87)
(70.87)
Soit:
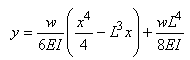 (70.88)
(70.88)
et comme la flèche est de toute façon en x
= 0, nous avons alors:
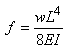 (70.89)
(70.89)
ÉQUATION DES POUTRES (EULER-BERNOULLI)
Considérons maintenant le cas d'une poutre encastrée
des deux côtés (cas encore plus courant que les
deux exemples précédents!). L'analyse va être
un peu plus difficile et il va nous falloir introduire plusieurs
concepts.
Une poutre en pratique doit résister aux efforts suivants:
- Tension ou compression:

- Cisaillement (effort tranchant):

- Flexion (effort fléchissant):

Si une poutre est en équilibre, alors les
efforts internes doivent satisfaire en tout point:
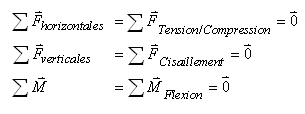 (70.90)
(70.90)
Considérons maintenant une poutre encastrée à ses
deux extrémités (poutre bi-encastrée) et
prenons en un tranche de longueur infinitésimale dy telle
que localement sa courbure soit nulle. La poutre sera supposée
soumise à une
force (poids) uniforme sur toute sa longueur (force qui peut
aussi être assimilée à son propre poids comme
nous l'avons déjà précisé plus haut).
Il est alors d'usage de noter 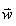 la
force par unité de longueur (poids total divisé par
la longueur) qui est bien évidemment une charge linéique: la
force par unité de longueur (poids total divisé par
la longueur) qui est bien évidemment une charge linéique:

Si la poutre est à l'équilibre
une fois déformée
(faiblement ou beaucoup déformée cela importe peu!)
alors les sommes des forces de tension, compression, cisaillement
et flexion
doivent être nulles en chaque point comme nous l'avons
déjà dit!
Cela ne veut cependant pas dire qu'en chaque point de la
ligne élastique les valeurs de chacun des forces est égale! Bien
au contraire. Il y a bien évidemment des différences (sinon quoi
il n'y aurait pas déformation).
Faisons alors d'abord la somme des forces locales
de tension et de compression (horizontales) de l'élément
de longueur dy.
Nous avons alors schématiquement:

Soit algébriquement (le variationnel pouvant
être négatif ou positif peu importe!):
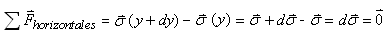 (70.91)
(70.91)
Si maintenant nous nous occupons des forces verticales
à la source du cisaillement. Nous avons alors schématiquement:

Soit algébriquement (le variationnel pouvant
être négatif ou positif peu importe!):
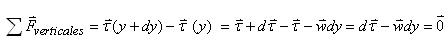 (70.92)
(70.92)
Et finalement pour les moments de flexion la somme
est aussi forcément nulle à l'équilibre.
Cependant contrairement aux deux sommes algébriques précédentes
où nous pouvions utiliser seulement le différentiel,
nous devons pour les moments de flexion choisir un point R de
référence
puisque pour rappel... le moment de force est par définition
le produit d'une force par une distance. Nous choisirons donc
naturellement le centre de gravité:

La charge linéaire
uniforme 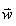 sur
la longueur dy génère une
de force à mi-distance
de: sur
la longueur dy génère une
de force à mi-distance
de:
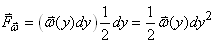 (70.93)
(70.93)
mais comme elle est confondue aux chois de notre
repère, alors son moment de force est nul!
Nous avons alors algébriquement: 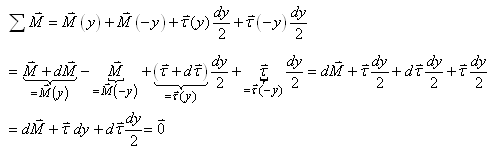 (70.94)
(70.94)
et si nous négligeons les différentiels d'ordre
deux:
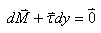 (70.95)
(70.95)
Nous avons donc au final:
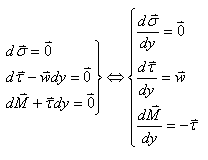 (70.96)
(70.96)
Pour déterminer le moment de fléchissement à partir
de la charge linéaire (ce qui intéresse en priorité le praticien),
nous dérivons deux fois la troisième relation et faisons une
substitution:
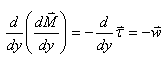 (70.97)
(70.97)
Soit:
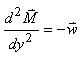 (70.98)
(70.98)
Le problème avec cette dernière relation
est la connaissance des moments. Il faudrait nous débarrasser
absolument de ce terme. Ce que nous connaissons facilement
c'est la fonction
de déformation et nous avons démontré plus
haut que:
 (70.99)
(70.99)
Il vient alors immédiatement en substituant
la relation précédente dans l'antéprécédente: 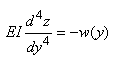 (70.100)
(70.100)
Il s'agit de la relation la plus important de la
théorie des poutres car elle permet en connaissance la
charge linéaire de déterminer la fonction de déformation
ou inversement! Elle est tellement important qu'on l'appelle "équation
des poutres"
ou encore en honneur à ceux qui l'ont déterminé: "équation
d'Euler-Bernoulli".
Comme il s'agit d'une équation différentielle d'ordre
4 qui va générer quatre constantes à chaque intégration, il nous
faudra alors 4 conditions initiales pour la résoudre complètement.
 Exemple: Exemple:
Nous souhaiterions calculer la déformation
d'une poutre fixée des deux côtés et chargée
uniformément connaissant
sa longueur L,
son module d'élasticité E, son moment
d'inertie I. Nous partons alors (nous changeons les
notations pour montrer que selon les ouvrages les axes pris peuvent
être notés différemment):
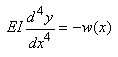 (70.101)
(70.101)
avec les conditions initiales:
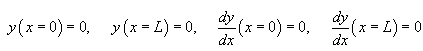 (70.102)
(70.102)
Et intégrant à répétition, nous avons:
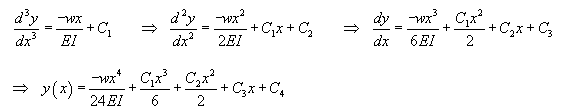 (70.103)
(70.103)
Des deux conditions initiales:
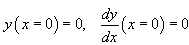 (70.104)
(70.104)
Il en découle que:
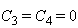 (70.105)
(70.105)
Avec les deux autres conditions restantes, nous
obtenons le système suivant qui doit nous permettre de déterminer
les deux constantes restantes:
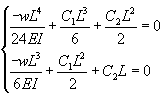 (70.106)
(70.106)
Après il s'agit simplement de résoudre un simple
système linéaire (cf. chapitre
d'Algèbre Linéaire):
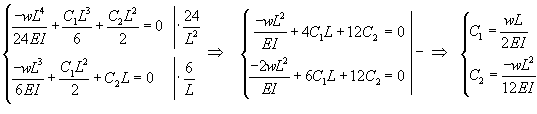 (70.107)
(70.107)
Donc une poutre bi-encastrée idéale
soumise à une
charge uniforme et décrite par:
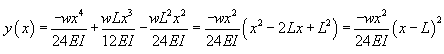 (70.108)
(70.108)
Pour déterminer la flèche, il nous faut donc chercher
le point x où cette relation a un optimum. Nous avons alors:
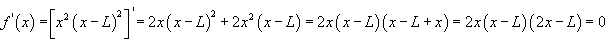 (70.109)
(70.109)
Il s'ensuite que la flèche à un maximum en x =
L/2.En injectant cela dans y(x) nous
obtenons la fameuse relation souventé donnée dans la littérature
mais rarement démontrée:
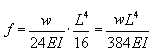 (70.110)
(70.110)
Il s'ensuit que la flèche d'une poutre est proportionnelle à la
puissance quatrième de la longueur de la poutre! Une si forte
dépendance impose des limitations significatives dans les constructions
civiles basées sur des poutres.
Remarque: La charge linéique
constante, soit sur la longueur totale de la poutre, soit par
tronçons successifs,
est une sollicitation fréquente dans les pièces à axe
horizontal. Elle peut provenir du poids propre de la pièce à section
constante ou d'une charge provoquée par une poussée
extérieure (gravité
par exemple).
énergie potentielle élastique
Après un survol rapide des diverses déformations élastiques
des pièces sollicitées par les efforts fondamentaux,
nous allons
établir ici l'expression générale de l'énergie élastique
accumulée
dans une barre de forme quelconque sollicité par des efforts
extérieurs.
Rappelons pour cette étude que nous pouvons écrire
la loi de Hooke (cf. chapitre de Mécanique Des Milieux Continus)
sous la forme suivante:
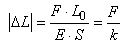 (70.111)
(70.111)
et l'énergie potentielle élastique d'un ressort
démontrée dans le chapitre de
Mécanique
Classique est donnée par:
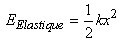 (70.112)
(70.112)
ou en déplacement relatif:
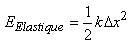 (70.113)
(70.113)
Dans le domaine de traction (ou compression)
longitudinale des barres, il est d'usage de considérer
la barre comme un ressort (...) et alors d'utiliser la constante
de
raideur de la loi de Hook... en espérant que cela colle à l'expérience:
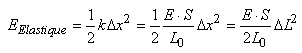 (70.114)
(70.114)
où conformément à l'usage,
nous notons le déplacement
longitudinal L au lieu de x. En injectant la
loi de Hook (oui... ça tourne un peu en rond...):
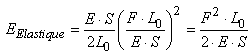 (70.115)
(70.115)
Il suffit alors de diviser par la longueur de la
barre pour avoir l'énergie linéique élastique:
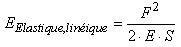 (70.116)
(70.116)
L'énergie volumique, notée traditionnellement comme
en thermodynamique par une minuscule, est alors:
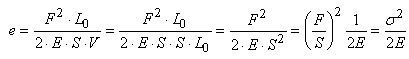 (70.117)
(70.117)
TORSION
Rappelons au lecteur d'abord une étude faite dans le
chapitre de Mécanique Classique sur le pendule de torsion
où certains éléments
avaient volontairement tus. Étudions cela plus en détails
car très utile pour les arbres de transmission ou les
ressorts dans la vie de tous les jours.
Considérons maintenant un fil cylindrique fixé en
sa base et soumis à un
moment de torsion  .
Sous l'effet de ce moment de torsion, la face supérieure
du fil est décalée d'un angle .
Sous l'effet de ce moment de torsion, la face supérieure
du fil est décalée d'un angle  par
rapport à la face inférieure, la matière subissant
une tension de torsion (ou cisaillement par
rapport à la face inférieure, la matière subissant
une tension de torsion (ou cisaillement ): ):

Figure: 70.16 - Fil sous torsion
Imaginons à l'intérieur du fil un tube élémentaire de rayon r,
d'épaisseur dr, et observons l'effet de la torsion sur
ce tube déroulé (cela nous permettra une approche approximative
du phénomène intéressé):

Figure: 70.17 - Extraction un élément du fil sous torsion
Cherchons une relation entre le moment de torsion  et
l'angle de torsion et
l'angle de torsion  . .
Pour le tube déroulé, appliquons les relations du cisaillement:
 (70.118)
(70.118)
or la figure montre que (les déformations étant
faibles) au premier ordre en série de Taylor (cf.
chapitre sur les Suites et Séries):
 (70.119)
(70.119)
d'où:
 (70.120)
(70.120)
Le moment élémentaire dû à cette force est par définition du
moment de force:
 (70.121)
(70.121)
Soit puisque  et et  sont
perpendiculaires: sont
perpendiculaires:
 (70.122)
(70.122)
Le moment total vaut alors:
 (70.123)
(70.123)
donc:
 (70.124)
(70.124)
Nous retrouvons donc la relation du pendule de torsion que
nous avions posé lors de notre étude du pendule
de torsion dans le chapitre de Mécanique Classique avec
comme différence que
cette fois la constante k, la "constante
de torsion" est
explicite!!!!
Le numérateur de la constante k est appelé dans
le domaine dans la résistance des matériaux "rigidité
torsionnelle" et la constante k elle-même
est souvent appelée "raideur
de l'arbre" au
lieu de "constante de torsion". Dans la pratique on
cherche surtout à trouver la valeur numérique de
l'expression suivante:
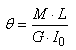 (70.125)
(70.125)
puisque cela donnera l'amplitude angulaire de la torsion.
Voyons donc une application très importante au ressort de compression
de type hélicoïdal (l'approche est approximative à nouveau à défaut
de mieux...) travaillant en torsion.
D'abord il faut bien se rendre compte que lorsqu'une force
est appliquée au ressort, les extrémités vont tourner d'un angle  alpha
faible (torsion) correspondant au parcours d'une distance x qui
elle-même correspond au rétrécissement du ressort (ben oui! il
faut bien que cette longueur soit reprise quelque part). alpha
faible (torsion) correspondant au parcours d'une distance x qui
elle-même correspond au rétrécissement du ressort (ben oui! il
faut bien que cette longueur soit reprise quelque part).
Soit alors un ressort de rayon extérieur R (soit
de diamètre D), de module de cisaillement G, avec
un diamètre de corps d (diamètre du cylindre plié dont
est composé le ressort):

Figure: 70.18 - Ressort spiral sous effort
Pour l'analyse nous aurons besoin simplement de mélanger
plusieurs de relations démontrées jusqu'à maintenant.
En premier lieu l'angle de torsion d'une poutre de longueur L (longueur
du ressort en l'occurrence!):
 (70.126)
(70.126)
Avec:
 (70.127)
(70.127)
et:
 (70.128)
(70.128)
Par ailleurs, le moment de torsion s'écrit:
 (70.129)
(70.129)
Nous arrivons donc à:
 (70.130)
(70.130)
Remarque: Le rapport  ,
au même titre que pour l'arbre, est
appelé la " raideur du ressort".
Le déplacement (déformation) x vaut lui (cf.
chapitre de Trigonométrie):
 (70.131)
(70.131)
Nous arrivons finalement à:
 (70.132)
(70.132)
ce qui nous amène à la relation mondialement connue dans le
monde dans la R.D.M. en ce qui concerne les ressorts:
 (70.133)
(70.133)
où k est la constante de "raideur
du ressort"!! Si maintenant, nous utilisons l'expression
de l'énergie
potentielle élastique d'un
ressort démontrée
dans le chapitre de Mécanique Classique:
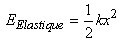 (70.134) (70.135)
(70.134) (70.135)
nous pouvons alors déterminer l'énergie qu'un ressort
spiral peut absorber.
FLAMBAGE
Nous terminons cette étude de la R.D.M. avec le flambage (cas
d'étude classique en construction et mécanique) qui consiste à déterminer
(dans un cas particulier simple) la force minimale  à partir
de laquelle une barre de longueur L, de module de Young E fixée à ses
deux extrémités peut plier (avec un rayon R) jusqu'à casser
sans qu'il y ait besoin de trop augmenter la force à partir
de laquelle une barre de longueur L, de module de Young E fixée à ses
deux extrémités peut plier (avec un rayon R) jusqu'à casser
sans qu'il y ait besoin de trop augmenter la force  (il
s'agit donc à nouveau d'une valeur d'indication!). (il
s'agit donc à nouveau d'une valeur d'indication!).
Dans l'étude de ce phénomène, nous considérons que dès que
la barre commence à plier nous avons alors  (et
nous ne sommes alors plus très loin de la force permettant de
la casser). (et
nous ne sommes alors plus très loin de la force permettant de
la casser).

Figure: 70.19 - Exemple de flambage
Lorsque la barre commence à plier nous avons alors une force  qui
s'applique à chaque élément de volume de la barre
mais comme ceux-ci ne sont pas distribués de la même manière
selon l'axe z, ils ne créent pas le même moment
de force! qui
s'applique à chaque élément de volume de la barre
mais comme ceux-ci ne sont pas distribués de la même manière
selon l'axe z, ils ne créent pas le même moment
de force!
À l'équilibre de la force de flambement, la barre
soumet un moment de rappel. Nous avons alors:
 (70.136)
(70.136)
En exprimant le moment de flexion M au moyen de la relation:
 (70.137)
(70.137)
Il vient:
 (70.138)
(70.138)
En utilisant l'équation de la ligne élastique
et en substituant, nous obtenons:
 (70.139)
(70.139)
soit:
 (70.140)
(70.140)
qui est l'équation différentielle de flambage permettant de
calculer la force de flambage avec les conditions initiales:
 (70.141)
(70.141)
Indiquons que la relation:
 (70.142)
(70.142)
est très souvent écrite sous la forme suivante dans la littérature:
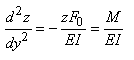 (70.143)
(70.143)
La résolution de l'équation différentielle
du second ordre:
 (70.144)
(70.144)
est relativement aisée (cf.
chapitre de Calcul Différentiel Et Intégral)
puisque l'équation caractéristique est:
 (70.145)
(70.145)
Nous avons alors la solution homogène:
 (70.146)
(70.146)
La condition  impose: impose:
 (70.147)
(70.147)
Il vient alors:
 (70.148)
(70.148)
La deuxième condition  impose: impose:
 (70.149)
(70.149)
Donc il vient immédiatement que:
 (70.150)
(70.150)
avec  (car k valant
zéro
n'est pas une solution physique possible et k entier supérieur à 1
signifierait que la barre plie sur plusieurs périodes
ce qui n'est pas le cas puisqu'elle le fait seulement sur une
demi-période comme le montrait la figure plus haut).
Soit: (car k valant
zéro
n'est pas une solution physique possible et k entier supérieur à 1
signifierait que la barre plie sur plusieurs périodes
ce qui n'est pas le cas puisqu'elle le fait seulement sur une
demi-période comme le montrait la figure plus haut).
Soit:
 (70.151)
(70.151)
Cette relation est parfois appelée "formule
d'Euler" (à ne
pas confondre avec la formule du même nom en théorie des
graphes) et la charge limite la "charge
ou force critique d'Euler" pour une poutre parfaitement
encastrée aux extrémités. L'ensemble de l'étude étant
le "flambage
d'Euler".
TRACTION
Considérons maintenant le cas d'une barre suspendue seulement à son
propre poids. La surface de sa section circulaire est S et h la
hauteur totale de cette barre. Le module de Young du matériau est
noté E (cf. chapitre de Mécanique
des Milieux Continus)
et  sa
masse volumique. sa
masse volumique.
Il est facile de constater qu'une section située à une altitude z supporte
le poids du morceau de barre situé sous elle:
 (70.152)
(70.152)
La contrainte n'est alors pas constante dans la barre:
 (70.153)
(70.153)
et la déformation non plus:
 (70.154)
(70.154)
z étant l'abscisse sur la barre, la déformation inhomogène
est liée au déplacement par la relation:
 (70.155)
(70.155)
Après intégration, nous obtenons la forme générale du déplacement:
 (70.156)
(70.156)
où la constante est à déterminer en utilisant les éventuelles
conditions de liaison aux extrémités de la barre. Si l'extrémité supérieure
est encastrée, le déplacement y est donc nul:
 (70.157)
(70.157)
Le déplacement en tout point de la barre s'exprime donc:
 (70.158)
(70.158)
L'allongement de la barre est l'écart en déplacement entre les
deux extrémités de la barre:
 (70.159)
(70.159)
Nous avons alors trivialement:
 (70.160)
(70.160)
|