|

GÉNIE MARIN & MÉTÉO | GÉNIE
MÉCANIQUE | GÉNIE ÉLECTRIQUE
GÉNIE ÉNERGÉTIQUE | GÉNIE
CIVIL | GÉNIE BIOLOGIQUE | GÉNIE
AÉROSPATIAL
GÉNIE
CHIMIQUE | GÉNIE INDUSTRIEL |
GÉNIE LOGICIEL
Dernière mise à jour
de ce chapitre:
2015-09-06 16:36:47 | {oUUID 1.799}
Version: 3.0 Révision 3 | Rédacteur: Vincent ISOZ |
Avancement:
~20%
 vues
depuis
le 2012-01-01:
4'358 vues
depuis
le 2012-01-01:
4'358
 LISTE DES SUJETS TRAITÉS SUR CETTE PAGE
LISTE DES SUJETS TRAITÉS SUR CETTE PAGE
Le Génie Logiciel sera défini
dans ce chapitre comme l'ensemble des techniques ou approches de
résolution de problèmes utilisant fortement des mathématiques
de niveau universitaire et que nous retrouvons (ou trouvions...)
fréquemment
implémentés dans de nombreuses solutions
informatiques.
Le lecteur retrouvera dans les textes qui vont suivre
des outils mathématiques dont les détails ont tous été démontrés
dans
d'autres chapitres, mais dont les mises en applications informatiques
n'avaient pas leur place dans la partie purement théorique.
Remarque: Si le lecteur cherche les méthodes mathématiques
pour simuler des objets 3D sur un écran, il devra se reporter au
chapitre de Géométrie Projective.
ALGORITHME PAGERANK DE GOOGLE
Lors de sa création en 1998 Google (moteur de recherche actuellement
très connu des internautes) a dominé et domine encore en 2011 le
marché des moteurs de recherche sur Internet. Son point fort initial
est basé sur l'idée très simple de trier les résultats par ordre
de pertinence, ce que ne faisaient pas les autres grands moteurs
de recherche avant lui.
L'idée principale du principe de fonctionnement initial
de Google est intéressante à présenter sur
ce site, car elle est un exemple pratique de concepts purement
mathématiques que nous avons
présentés jusqu'ici (théorie des graphes et
chaînes de Markov dans les chapitre respectifs de Théorie
des Graphes et de Probabilités) et qui ont créé l'une
des plus grandes entreprises internationales dans les nouvelles
technologies
dans
les années
2000 (Google gagne des milliards avec l'algèbre linéaire...)!
Comme c'est souvent le cas dans l'économie de marché,
ce sont d'abord des recherches théoriques (mathématiques
ou physiques) qui ont permis de développer
de nouveaux outils!
Remarques:
R1. Évidemment l'algorithme de base a changé depuis 1998
car on peut y rajouter beaucoup de paramètres mathématiques (pondération
par une distance par exemple) ou empiriques (visites, clics, publicités
...).
R2. Cet algorithme n'est pas utilisé que dans le domaine du web.
Effectivement, il peut être utilisé pour mettre en évidence
n'importe quel objet en relation multiple avec d'autres objets
(par exemple des variables dans un projet qui s'influencent les
unes des autres en ayant des relations directes ou indirectes:
une analyse structurelle).
Pour trouver une information dans le tas amorphe et non vraiment
structuré qu'est le web (vu le peu de gens qui respectent correctement
les standards émis par le W3C...), l'utilisateur lancera une recherche
par mots-clés. Ceci nécessite bien évidemment une certaine préparation
pour être efficace: le moteur de recherche copie préalablement
les pages web en mémoire locale et trie les mots (ou composition
de mots) par ordre alphabétique en utilisant les algorithmes d'index
empiriques traditionnels du domaine de l'informatique (arbres-b,
arbres-b+ ou autres encore...). Le résultat est un annuaire de
mots-clés avec leurs pages web associées.
Afin d'analyser comment Google identifie les pages web les plus
pertinentes, nous allons négliger le contenu des pages et ne
compter que les liens entre elles. Ce que nous obtenons alors est
la structure d'un graphe (non nécessairement connexe!).
L'image
suivante montre un exemple miniature (il y aurait 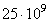 sites
web d'après Google début 2007): sites
web d'après Google début 2007):

Figure: 75.1 - Principe schématique
du graphe à étudier
Pour la suite, nous noterons les pages web par:
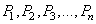 (75.1)
(75.1)
et nous écrirons:
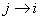 (75.2)
(75.2)
si la page 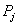 cite
directement la page cite
directement la page 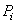 (citation
directement connexe). Ainsi, dans l'image précédente, nous avons
un lien (citation
directement connexe). Ainsi, dans l'image précédente, nous avons
un lien 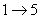 ,
par exemple, mais pas de lien ,
par exemple, mais pas de lien 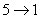 . .
Bien évidemment, un lien 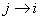 est
une recommandation de la page est
une recommandation de la page 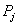 d'aller
lire la page d'aller
lire la page 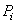 .
C'est ainsi un vote de .
C'est ainsi un vote de 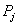 en
faveur de l'autorité de la page en
faveur de l'autorité de la page 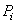 (nous
comprenons alors aisément pourquoi l'échange de liens entre sites
n'ayant aucun rapport contextuel ait été en quelque
sorte bannie par Google). (nous
comprenons alors aisément pourquoi l'échange de liens entre sites
n'ayant aucun rapport contextuel ait été en quelque
sorte bannie par Google).
Analysons l'image précédente sous un aspect plus conforme à la
théorie des graphes, dont la hiérarchie devra être justifiée par
la suite:

Figure: 75.2 - Graphe précédent réarrangé
Pour des raisons purement pédagogiques, nous allons introduire
trois modèles théoriques de ranking de pages web. Le dernier modèle étant
le plus proche de celui implémenté par Google en 1998 et les deux
premiers modèles permettant de préparer le terrain.
COMPTAGE PONDÉRÉ
Il est fortement plausible que si une page est importante, elle
reçoit beaucoup de liens. Avec un peu de naïveté, on peut penser
que la réciproque est vraie (une page qui reçoit beaucoup de liens
est importante). Ainsi, nous pourrions définir l'importance 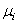 d'une
page d'une
page 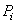 comme étant
le nombre de liens comme étant
le nombre de liens 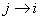 directement
connexes. Sous forme mathématique, nous écrirons cela ainsi: directement
connexes. Sous forme mathématique, nous écrirons cela ainsi:
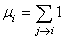 (75.3)
(75.3)
Autrement dit, 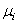 est égal
au nombre de votes pour la page est égal
au nombre de votes pour la page 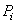 ,
où chaque vote contribue par la même valeur 1. Cela est, certes,
facile à calculer, mais ne correspond souvent pas à l'importance
ressentie par l'utilisateur. ,
où chaque vote contribue par la même valeur 1. Cela est, certes,
facile à calculer, mais ne correspond souvent pas à l'importance
ressentie par l'utilisateur.
Dans notre exemple, nous avons ainsi:
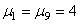 (75.4)
(75.4)
devant:
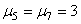 (75.5)
(75.5)
ce qui est pire, c'est que ce comptage naïf est trop facile à manipuler
en ajoutant des pages (d'un autre nom de domaine internet)
sans intérêt
recommandant une page quelconque.
Remarque: Donc le poids maximum est égal in extenso à n-1
Certaines pages émettent beaucoup de liens. Ceux-ci semblent
donc moins spécifiques (spécialisés) et leurs
poids sera dès lors
plus faible. Nous partageons donc le vote de la page 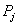 en en 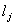 parts égales,
où parts égales,
où 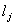 dénote
le nombre de liens émis. Ainsi, nous pouvons définir
une mesure plus fine: dénote
le nombre de liens émis. Ainsi, nous pouvons définir
une mesure plus fine:
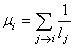 (75.6)
(75.6)
Autrement dit, 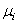 compte
le nombre de votes pondérés pour la page compte
le nombre de votes pondérés pour la page 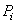 .
C'est facile à calculer, mais nous restons toujours avec le problème
susmentionné. .
C'est facile à calculer, mais nous restons toujours avec le problème
susmentionné.
Dans notre exemple, nous avons ainsi:
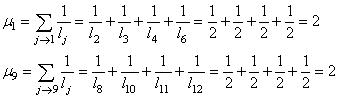 (75.7)
(75.7)
et:
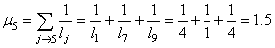 (75.8)
(75.8)
et:
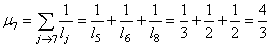 (75.9)
(75.9)
Remarque: Si toutes les pages étaient directement connexes, nous
aurions alors  pour
tout i.
COMPTAGE RÉCURSIF
Heuristiquement, une page 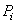 paraît
importante si beaucoup de pages importantes la citent. Ceci nous
mène à définir l'importance paraît
importante si beaucoup de pages importantes la citent. Ceci nous
mène à définir l'importance 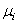 de
manière récursive comme suit: de
manière récursive comme suit:
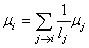 (75.10)
(75.10)
Il s'agit donc d'un système d'équations linéaires
homogène à n inconnues,
où dans l'exemple choisi 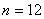 .
Plus traditionnellement, le système pourra être noté: .
Plus traditionnellement, le système pourra être noté:
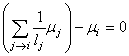 (75.11)
(75.11)
ou plus explicitement (cf. chapitre d'Algèbre Linéaire):
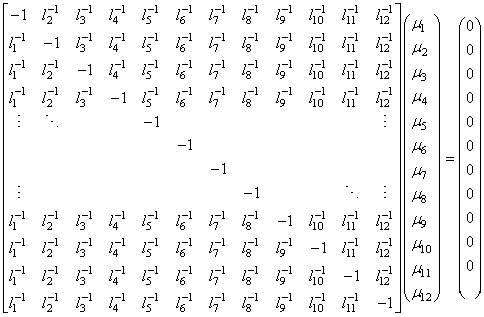 (75.12)
(75.12)
Ce qui donne avec les valeurs de notre exemple:
 (75.13)
(75.13)
Outre la solution triviale (vecteur nul), ce système à une
infinité de
solutions car son déterminant est nul (cf.
chapitre d'Algèbre Linéaire),
ce que l'on peut facilement vérifier avec la fonction MDETERM(
) de la version anglaise de Microsoft Excel 11.8346.
Notons maintenant le système précédent sous la forme:
 (75.14)
(75.14)
Nous remarquons deux choses avant de continuer:
1. Dans la matrice ci-dessus, chaque colonne est telle que la
somme de ses valeurs égale l'unité. Il s'agit
donc de la transposée
d'une matrice stochastique d'une chaîne de Markov (cf.
chapitre de Probabilités).
2. L'importance 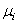 est
positive ou nulle. Donc le vecteur est
positive ou nulle. Donc le vecteur 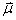 est
strictement positif et il s'agit du vecteur stochastique de
la chaîne de Markov (cf. chapitre de
Probabilités) dont la somme
des composantes doit être égale à l'unité. est
strictement positif et il s'agit du vecteur stochastique de
la chaîne de Markov (cf. chapitre de
Probabilités) dont la somme
des composantes doit être égale à l'unité.
Nous écrirons alors ce système sous forme condensée:
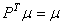 (75.15)
(75.15)
Ainsi, 1 est la valeur propre et 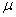 le
vecteur propre de l'application P. Nous savons de par notre étude
des chaînes de Markov que cette relation n'est vérifiée que pour
la mesure invariante notée traditionnellement le
vecteur propre de l'application P. Nous savons de par notre étude
des chaînes de Markov que cette relation n'est vérifiée que pour
la mesure invariante notée traditionnellement 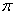 dans
le domaine d'étude des chaînes de Markov: dans
le domaine d'étude des chaînes de Markov:
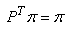 (75.16)
(75.16)
Pour déterminer la mesure, il faut d'abord réécrire
le réseau
sous le format d'application matricielle d'une chaîne de
Markov (cf. chapitre de Probabilités):
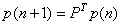 (75.17)
(75.17)
Avec Microsoft Excel 11.8346, la modélisation est
assez simple à reproduire
pour déterminer la mesure invariante avec un point de départ
quelconque (distribution quelconque) dans le graphe:

Figure: 75.3 - Détermination
de la mesure invariante avec Microsoft Excel 11.8346
avec les formules suivantes:

Figure: 75.4 - Formules Microsoft Excel
11.8346 (version anglaise) correspondantes au tableau précédent
Le système converge assez vite, après la 30ème étape, nous avons
déjà une convergence à la deuxième décimale:

Figure: 75.5 - Convergence à la 35ème
itération
Donc finalement la mesure invariante est:
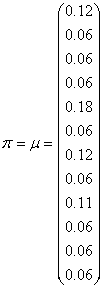 (75.18)
(75.18)
quelle que soit la distribution du vecteur de départ. Propriété que
l'on appelle "ergodique" dans le domaine des chaînes
de Markov.
Étant donné que, nous avons pour tout 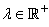 le
système suivant qui est toujours vérifié: le
système suivant qui est toujours vérifié:
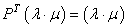 (75.19)
(75.19)
Alors, il est d'usage dans l'étude de l'algorithme de Google
d'écrire
le vecteur stochastique avec des valeurs entières (chaque valeur
du vecteur stochastique a été divisée par la plus petite probabilité qui était
0.06) correspondant au fameux "PageRank
Value" (au début
de l'existence de Google car actuellement ce calcul est beaucoup
plus subtil) tel que:
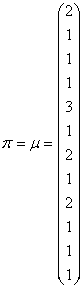 (75.20)
(75.20)
Cela nous donne donc la répartition convergente par page d'une
cohorte de 17 internautes (sommes des valeurs du vecteur stochastique).
Les pages où 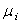 est
grand sont les plus fréquentées (les plus populaires) en termes
de probabilités à l'équilibre. Dans la quête de classer les pages
web, c'est encore un argument pour utiliser la mesure est
grand sont les plus fréquentées (les plus populaires) en termes
de probabilités à l'équilibre. Dans la quête de classer les pages
web, c'est encore un argument pour utiliser la mesure 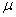 comme
indicateur empirique. comme
indicateur empirique.
ÉTATS ABSORBANTS
Cependant, si notre graphe (chaîne) contient une page (ou
un groupe de pages) sans issue alors celle-ci absorbe toute la
probabilité,
car notre cohorte tombera tôt ou tard sur cette page et ne
pourra plus en sortir (état absorbant comme défini dans
le chapitre de Probabilités). Nous représentons
cela sous la forme graphique suivante si, par exemple, nous ajoutons
une page 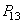 qui
est absorbante: qui
est absorbante:

Figure: 75.6 - Graphe avec un état absorbant
avec la matrice de transition associée:
 (75.21)
(75.21)
Notre modèle n'est donc pas encore satisfaisant. Nous pourrions
construire alors une matrice qui permet d'échapper aux états
absorbants en posant que toute colonne qui ne contient qu'un seul
1 avec que
des zéros se voit téléporter le visiteur sur
toutes les pages avec un poids égal. Ce qui donnerait puisque
nous avons 13 pages:
 (75.22)
(75.22)
Mais ceci n'est pas très optimal, car cela charge la matrice
donc c'est très gourmand en termes de mémoires et calculs.
Pour échapper aux états absorbants, Google utilise un modèle
empirique plus raffiné.
Nous prenons l'application initiale qui est une application linéaire:
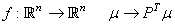 (75.23)
(75.23)
où pour rappel la somme des composantes de 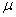 vaut
toujours 1. Nous réécrivons cela sous la forme: vaut
toujours 1. Nous réécrivons cela sous la forme:
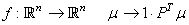 (75.24)
(75.24)
où le 1 représente le fait qu'il y a 100% de probabilité d'avoir
l'état 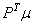 .
Maintenant, l'astuce consiste à écrire: .
Maintenant, l'astuce consiste à écrire:
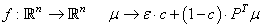 (75.25)
(75.25)
avec:
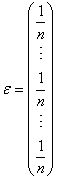 (75.26)
(75.26)
ce qui signifie que l'internaute a à tout moment une probabilité 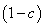 d'être
dans l'état d'être
dans l'état 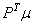 et
une probabilité c d'être dans l'état et
une probabilité c d'être dans l'état 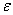 ,
c'est-à-dire de se trouver avec une probabilité équiprobable en
n'importe quel point du graphe. Enfin, nous sommons les deux pour
obtenir à nouveau un vecteur stochastique (dont la somme des composantes
vaut 1). ,
c'est-à-dire de se trouver avec une probabilité équiprobable en
n'importe quel point du graphe. Enfin, nous sommons les deux pour
obtenir à nouveau un vecteur stochastique (dont la somme des composantes
vaut 1).
Effectivement, si nous prenons par exemple 10% pour la valeur
de c, nous avons la somme des composantes du vecteur:
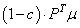 (75.27)
(75.27)
qui vaudra 0.9 et respectivement la somme des composantes du
vecteur 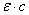 qui
vaudra 0.1 (puisque la somme des composantes de qui
vaudra 0.1 (puisque la somme des composantes de 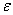 vaut
aussi 1 par construction). vaut
aussi 1 par construction).
Donc pour résumer, avec une probabilité fixée c le
moteur d'indexation (ou l'internaute) abandonne la page actuelle 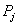 et
recommence sur une des n pages du web, celle-ci étant
choisie, afin de ne privilégier personne.
Sinon, avec une probabilité et
recommence sur une des n pages du web, celle-ci étant
choisie, afin de ne privilégier personne.
Sinon, avec une probabilité 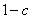 le
moteur suit un des liens de la page le
moteur suit un des liens de la page 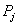 ,
choisi de manière équiprobable. Le seul point délicat
reste à calibrer
la valeur de c qui vaut donc entre 0 et 1. S'il vaut 0 nous
retombons sur le modèle initial avec le problème
des états absorbants,
s'il vaut 1 nous avons un modèle qui donne une note égale à chaque
page. Il faut donc plutôt choisir c avec des valeurs
faibles proches de 0. ,
choisi de manière équiprobable. Le seul point délicat
reste à calibrer
la valeur de c qui vaut donc entre 0 et 1. S'il vaut 0 nous
retombons sur le modèle initial avec le problème
des états absorbants,
s'il vaut 1 nous avons un modèle qui donne une note égale à chaque
page. Il faut donc plutôt choisir c avec des valeurs
faibles proches de 0.
Cette astuce de téléportation évite de se faire piéger par une
page absorbante et garantit d'arriver n'importe où dans le graphe,
indépendamment des questions de connexité.
Il convient de remettre le tout sous forme de composantes, nous
avons donc l'écriture (dont le deuxième terme converge):
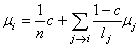 (75.28)
(75.28)
qui a l'avantage énorme de pouvoir calculer la valeur de n'importe
quelle composante 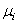 du
vecteur stochastique de n'importe quelle étape d'une promenade
aléatoire sur le graphe et ce sans faire appel à aucun moment à la
manipulation d'une immense matrice qui serait trop gourmande en
termes de capacités de mémoire!! du
vecteur stochastique de n'importe quelle étape d'une promenade
aléatoire sur le graphe et ce sans faire appel à aucun moment à la
manipulation d'une immense matrice qui serait trop gourmande en
termes de capacités de mémoire!!
|