|

PRINCIPES
| MÉCANIQUE ANALYTIQUE
| MÉCANIQUE
CLASSIQUE
MÉCANIQUE
ONDULATOIRE | MÉCANIQUE
STATISTIQUE | THERMODYNAMIQUE
MÉCANIQUE DES MILIEUX CONTINUS
|
34. MÉCANIQUE DES MILIEUX CONTINUS (3/3) |
Dernière mise à jour de ce chapitre:
2015-09-06 16:38:36 | {oUUID 1.814}
Version: 3.0 Révision 5 | Rédacteur: Vincent ISOZ |
Avancement:
~90%
 vues
depuis
le 2012-01-01:
1'914 vues
depuis
le 2012-01-01:
1'914
 LISTE DES SUJETS TRAITÉS SUR CETTE PAGE
LISTE DES SUJETS TRAITÉS SUR CETTE PAGE
GAZ
Les solides ont une forme
bien définie et sont difficiles à comprimer. Les
liquides peuvent s'écouler librement et leur écoulement
est limité par des surfaces autoformées. Les gaz
se dilatent librement pour occuper le volume du récipient
qui les contient, et ont une densité environ mille fois
inférieure à celle des liquides et des solides.
Ils conduisent peu la chaleur et l'électricité,
sauf si nous les ionisons (formation d'un plasma). Les molécules
d'un gaz neutre se déplacent suivant des trajectoires
rectilignes qui changent de direction à chaque collision
avec une autre molécule. Contrairement aux solides et
aux liquides, les interactions entre molécules restent
faibles. Les propriétés macroscopiques d'un gaz
se déduisent donc directement des propriétés
des molécules qui le composent (ou des atomes dans le
cas d'un gaz monoatomique).
TYPES
DE GAZ
En théorie des gaz (nous
parlons souvent de "théorie cinétique des gaz") nous
considérons toujours deux types de gaz neutres:
GAZ
PARFAIT
Il s'agit d'un modèle dans
lequel nous négligeons les interactions moléculaires
du gaz, à l'exception
des collisions, et dont le volume propre est négligeable
devant le volume du récipient. Nous déduisons de
ces considérations que le comportement
d'un gaz réel pourra être approché par
un gaz parfait si le volume qu'il occupe est suffisamment
grand, ce qui se produira à basse pression
et à température élevée. En pratique,
le modèle du gaz parfait donne des résultats satisfaisants
pour beaucoup de gaz usuels pris à la pression atmosphérique
et à la température ambiante (azote,
oxygène, vapeur d'eau,...).
Lorsqu'un gaz est à faible
pression, les interactions entre ses molécules sont faibles.
Ainsi, les propriétés d'un gaz réel à basse pression se rapprochent
de celles d'un gaz parfait. Nous pouvons alors décrire le comportement
du gaz par "l'équation d'état des
gaz parfaits" que nous démontrons plus bas lors de
notre étude du théorème du Viriel:
 (34.1)
(34.1)
avec n le nombre
de moles de gaz, P la pression du gaz, V le
volume occupé par les n moles et T la température
absolue du gaz. La constante R étant la constante des
gaz parfaits.
Cette équation montre que trivialement:
- À température T constante (système "isotherme"),
le volume d'une quantité fixée de gaz est inversement
proportionnel à sa pression. C'est la "loi
de Boyle-Mariotte":
Figure: 34.1 - Illustration de la loi de Boyle-Mariotte
De la loi de Boyle-Mariotte, nous déduisons qu'à température constante
(donc lors d'une transformation isotherme):
(34.2)
- À pression P constante (système "isobare"),
le volume d'une quantité fixée de gaz est proportionnel à la
température absolue. C'est la "loi
de Gay-Lussac" (dans le cas des gaz parfaits...):

Figure: 34.2 - Illustration de la loi de Gay-Lussac
C'est cette relation qui est souvent utilisée dans les
labos des petites classes pour montrer qu'avec une extrapolation
de la droite
mesurée, le volume devient théoriquement... nul à une
température
d'environ -273.15 [°C]. Non sérieusement à partir
d'une certaine température, il faut utiliser des modèles
quantiques et de plus cette relation n'est valable vraiment que
pour les gaz (ainsi,
lorsque la vapeur d'eau devient liquide... ce n'est plus valable).
Rappelons aussi que nous avons démontré une expression
plus élaborée
de la loi de Gay-Lussac dans le chapitre de Thermodynamique en
faisant
usage
des équations
d'état et des coefficients thermoélastique... :
(34.3)
Comme
quoi elle n'a plus vraiment le satut de "loi" mais plutôt
d'équation! Nous avons aussi démontré dans
le chapitre de Thermodynamique que cette relation loi n'est qu'approchée
aux hautes pressions pour les gaz puisque qu'on les considère
incompressibles comme des liquides pour obtenir la relation en
question.
- À volume V constant (système "isochore"),
la pression d'une quantité fixée de gaz est proportionnelle à sa
température absolue. C'est la "loi
de Charles":
Figure: 34.3 - Illustration de la loi de Charles
Par la suite,
Amedeo Avogadro, à qui l'on doit le vocabulaire de "molécule" affirme
le concept moléculaire des gaz et conclut que des volumes égaux
de gaz différents, pris dans les mêmes conditions
de température et de pression, contiennent le même
nombre de molécules (ce constat découle aujourd'hui
automatiquement de l'équation des gaz parfaits que nous
démontrerons plus loin). Cette propriété était appelée
"loi d'Avogadro et Ampère".
 Exemple: Exemple:
L'air dans une bouteille de plongée est initialement à la
pression 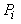 dans
un volume corresondant
à celui de la bouteille que nous supposerons être .
Un plongeur ne respire jamais directement l'air dans la bouteille à cause
de la pression qui y est environ 200 fois plus élevée
que la pression atomosphérique
lui
ferait exploser ses poumons. Une valve permet d'ajuster la pression
de l'air envoyée au plongeur afin qu'il soit égal à la
pression ambiant de la profondeur d'eau .
Il est intéressant de calculer le temps t que le
plongeur peut rester sous l'eau à une
profondeur de 10 mètres si on suppose qu'il consomme 0.03
mètres cube par minute. dans
un volume corresondant
à celui de la bouteille que nous supposerons être .
Un plongeur ne respire jamais directement l'air dans la bouteille à cause
de la pression qui y est environ 200 fois plus élevée
que la pression atomosphérique
lui
ferait exploser ses poumons. Une valve permet d'ajuster la pression
de l'air envoyée au plongeur afin qu'il soit égal à la
pression ambiant de la profondeur d'eau .
Il est intéressant de calculer le temps t que le
plongeur peut rester sous l'eau à une
profondeur de 10 mètres si on suppose qu'il consomme 0.03
mètres cube par minute.
Pour répondre à cette question il nous faut donc
déjà connaître
la pression à 10
mètres de profondeur. Pour cela nous
allons utiliser le théorème de Bernoulli démontré lors de notre étude
des fluides:
(34.4)
Ensuite, le volume dans la bouteille doit être mis
au volume de la pression ci-dessus en utilisant la loi de Boyle-Mariotte:
(34.5)
Nous avons alors comme volume équivalent:
(34.6)
Mais le piège est que le volume utilisable est moindre
car il faut encore de l'air pour pousser l'air restant. Il faut
alors soustraire les deux volumes:
(34.7)
et en divisant par une consommation volumique C standard
nous avons au final:
(34.8)
Pour en revenir l'équation d'état des gaz parfaits:
 (34.9)
(34.9)
GAZ
RÉEL
L'équation d'état des gaz
parfaits est approximative. Par exemple, un gaz parfait ne pourrait
ni se liquéfier ni se solidifier, quels que soient le refroidissement
et la compression auxquels il est soumis. Les gaz réels, surtout
dans des conditions de pression et de température proches de
la transition à l'état liquide, peuvent présenter des écarts
considérables avec la loi des gaz parfaits!
Il faut donc l'adapter
aux cas réels. Pour cela, nous utilisons l'équation
d'état
de Van der Waals qui est particulièrement
utile et bien connue. Elle peut être obtenue de manière
qualitative une fois l'équation des gaz parfaits démontrée
et est alors donnée
par (voir plus bas comment nous l'obtenons):
(34.10)
pour une mole, a et b étant
des paramètres adaptables déterminés par des mesures
expérimentales
effectuées sur le gaz concerné. Ce sont des paramètres
qui varient d'un gaz à un autre.
L'équation de Van der
Waals peut également être interprétée au niveau microscopique. Les
molécules interagissent les unes avec les autres. Cette interaction
est fortement répulsive pour les molécules proches les unes des autres,
devient légèrement attractive pour un éloignement moyen et disparaît
lorsque l'éloignement est important. À pression élevée, la loi des
gaz parfaits doit être rectifiée pour prendre en compte les forces
attractives ou répulsives.
THÉORÈME
DU VIRIEL
Nous allons ici aborder une étude des gaz parfaits
via une méthode particulière. Elle permet d'obtenir
un résultat intéressant et particulièrement
pour l'astrophysique (cf. chapitre d'Astrophysique).
Le théorème du Viriel permet également d'obtenir
d'autres résultats très intéressants mais
qui pédagogiquement sont un peu difficiles d'accès.
Le lecteur qui serait intéressé par cette deuxième
partie de résultats pourra directement se reporter un peu
plus loin où les concepts de pression et de température
cinétique sont traités.
Par définition, "l'expression
du Viriel" d'un
point matériel est le scalaire:
(34.11)
Par définition, le "Viriel" d'un
système composé de N points matériels est:
(34.12)
Soumis à une force centrale,
le Viriel s'écrit (par les propriétés du produit scalaire):
(34.13)
Le "théorème du Viriel"
s'énonce ainsi: Pour un système en équilibre (!), l'énergie
interne est égale à l'opposé de son demi-Viriel total lorsque
toutes les particules sont repérées par rapport à son
centre de masse.
Démonstration:
Soit la relation mathématique:
(34.14)
Sa dérivée seconde:
(34.15)
En multipliant par et
en sommant sur i:
(34.16)
Or:
(34.17)
et:
(34.18)
Donc:
(34.19)
Cette dernière expression
est valable quelle que soit la position d'un système de coordonnées
adopté. Cependant, il est intéressant de placer son origine au
centre de masse du système car nous ne sommes plus dépendants
de son mouvement.
Si le système est en équilibre,
les quantités macroscopiques qui la caractérisent ne sont pas
dépendantes du temps. Nous en concluons alors que la somme de
n'importe quelle quantité attachée à n'importe quel point matériel
du système est en fait une quantité dudit système.
Ainsi, est
une quantité macroscopique indépendante du temps. Cela implique
que:
(34.20)
Ce qui s'écrit encore (nous
multiplions par ½ des deux côtés):
(34.21)
Nous avons donc finalement:
(34.22)
Cette expression de l'énergie cinétique est connue
sous le nom de "théorème de
Viriel" et
le membre de droite est donc appelé le "Viriel
du système".
 C.Q.F.D. C.Q.F.D.
Nous noterons que:
(34.23)
où est
l'énergie cinétique totale associée à l'ensemble des points matériels
du système. Nous l'appelons "l'énergie
interne du système" et les thermodynamiciens la note
souvent avec la lettre U. est
l'énergie d'un point matériel quelconque du système.
Il est possible de retrouver
l'expression du Viriel à partir d'un système de particules (nuage
en accrétion). Strictement, l'équilibre n'existe pas dans un
tel cas. Néanmoins, nous pouvons admettre que si la contraction
gravitationnelle est suffisamment lente alors ses différentes
phases peuvent être considérées comme une succession d'états
d'équilibre.
Dans le cas d'une force
centrale et dérivant d'un potentiel, nous pouvons écrire:
(34.24)
et donc:
(34.25)
Si l'énergie potentielle
est de la forme k/r (ce qui est
le cas pour le potentiel électrique et gravitationnel) alors
il vient:
(34.26)
et il reste:
(34.27)
En résumé, le théorème
du Viriel nous donne une relation entre les énergies
cinétiques
et potentielles totales. Pour être valable, le mobile doit
décrire
une trajectoire autour du centre de force central et rester
indéfiniment dans un volume fini (état lié).
Ce type de raisonnement est applicable à un très grand nombre
de phénomènes, depuis
la structure de certaines galaxies jusqu'au dégagement
d'énergie
dans les explosions nucléaires en passant par l'étude
du Soleil et le comportement des gaz réels. Il s'agit
du premier résultat
qui nous intéressait.
Dans un système
gazeux, l'énergie potentielle peut s'écrire comme
la somme de l'énergie des forces agissant de l'extérieur
plus celles qui sont internes même au gaz. Tel que:
(34.28)
Or les forces internes
peuvent s'écrire comme:
(34.29)
Il ne faut pas dans cette
somme prendre la force qu'exerce chacune des particules sur elle-même.
Tel que:
(34.30)
Ce qui nous donne:
(34.31)
Dans la double somme,
nous pouvons regrouper les termes deux à deux et utiliser le
principe d'action-réaction tel que:
(34.32)
Pour obtenir:
(34.33)
Ce qui finalement nous
donne:
(34.34)
Et:
(34.35)
Le premier terme
de droite fait intervenir les forces intérieures (interactions)
entre les (paires de) particules et le deuxième terme de droite
fait intervenir les forces extérieures.
Considérons maintenant
un gaz contenu dans un récipient. Ses molécules ne sont sujettes à des
forces extérieures que lorsqu'elles heurtent une paroi et nous
imaginons qu'en moyenne cette force est perpendiculaire à la
paroi (chocs élastiques).

Figure: 34.4 - Gaz contenu dans un récipient
Pour toutes les faces contenues
dans les plans définis par les axes, nous avons toujours:
(34.36)
Puisqu'en moyenne est
toujours perpendiculaire à .
Pour les autres faces (BCFE par
exemple) nous avons et
donc:
(34.37)
où nous appelons a la
coordonnée selon Oy de l'extrémité de (ne
pas confondre avec l'accélération!).
Dès lors pour chaque face:
(34.38)
Effectivement car la pression interne du système sur les
parois est définie par:
(34.39)
Par le théorème du Viriel,
en ajoutant les contributions non nulles des faces BCFE, DEFG et ABED,
il vient:
(34.40)
Si l'énergie cinétique
moyenne d'une molécule est:
(34.41)
L'énergie cinétique moyenne
totale pour N molécules est alors (nous reviendrons
sur cette relation plus loin mais avec une autre approche):
(34.42)
ce que les thermodynamiciens notent souvent:
(34.43)
où U est donc l'énergie interne du gaz
et ddl le
nombre de degrés de liberté des constituants.
La relation antéprécédente, appelée "théorème
d'équipartition de l'énergie", est importante
car elle permet:
1. Une interprétation
microscopique de température T et de déterminer
l'énergie interne d'un gaz parfait monoatomique (et par
extension d'autres gaz avec des degrés de liberté autres).
2. De constater que le système de température en
Celsius n'est pas adapté à la réalité physique.
Effectivement, dans le système
utilisant les Celsius, à 0 [°C] tout devrait être
immobile (énergie
cinétique nulle) or il est évident que ce n'est pas
le cas pour toutes les substances. Donc il faut introduire une
nouvelle température
qui met en adéquation l'énergie cinétique
mesurée et la température
traditionnelle. Il s'agira de la "température
absolue" mesurée en Kelvin [K] dont
l'équivalence énergie cinétique/température
mesurée est telle que
le 0 [°C] correspond à 273.15 [K].
L'énergie interne est une contribution à l'énergie
qui n'apparaît
pas en mécanique classique. Du point de vue macroscopique,
un récipient
immobile qui contient un fluide ne possède pas d'énergie
cinétique,
alors que son énergie potentielle est constante. Nous pouvons
l'ignorer en donnant la valeur zéro à cette constante.
Du point de vue microscopique, les choses changent cependant!
Effectivement, les atomes ou molécules du fluide sont en
mouvement et interagissent. Il faut leur associer une énergie
(l'énergie
interne) qui est la somme des contributions relatives à chaque
atome.
Dès lors:
(34.44)
C'est "l'équation
générale d'état d'un gaz réel",
c'est-à-dire l'équation
d'état qui tient compte des interactions entre molécules.
Il est intéressant de remarquer que finalement cette
relation peut nous permettre de calculer l'énergie du
gaz même s'il n'y
pas de parois!
Si le gaz est parfait,
il n'y a pas d'interactions entre les N molécules (par
hypothèse)
et alors nous avons "l'équation des
gaz parfaits" suivante:
(34.45)
Que nous retrouvons beaucoup plus fréquemment sous la forme:
 (34.46)
(34.46)
si n est exprimé en moles avec R la
constante des gaz parfaits.
Si la température est constante, nous retrouvons la "loi
de Boyle-Mariotte":
(34.47)
Pour arriver à l'équation des gaz parfaits, il est utile
de rappeler que nous avons fait trois hypothèses:
H1. Les molécules
sont assimilées à des sphères dures dont
le diamètre est négligeable devant la distance
moyenne qui les sépare. C'est que ce que nous appelons "l'hypothèse
structurale".
H2. À la limite, et c'est
ce que nous avons retenu, si nous considérons les molécules
comme ponctuelles, la possibilité d'interaction entre
les particules s'annule. Les seules interactions qui subsistent
seront les chocs sur les parois du récipient qui contient
le gaz. Ces chocs sont parfaitement élastiques de sorte
que nous puissions appliquer les lois de conservation de la quantité de
mouvement de l'énergie cinétique. C'est ce que
nous appelons "l'hypothèse
interactive limite"
H3. Le gaz est étudié dans
un état d'équilibre thermodynamique ce qui se traduit
par l'homogénéité des variables intensives
et extensives. C'est que ce que nous appelons "l'hypothèse
du chaos moléculaire".
Dans un cas particulier,
si les interactions dérivent d'un potentiel central:
(34.48)
Il vient ainsi:
(34.49)
Si en outre l'énergie potentielle
est du type (attention de ne pas confondre le paramètre k avec
la constante de Boltzmann notée de la même manière!):
(34.50)
nous avons:
(34.51)
et dès lors:
(34.52)
où est
l'énergie totale moyenne du système.
Au fait, il faut bien prendre
garde au fait que nous n'avons pas rigoureusement démontré l'équation
des gaz parfaits. Effectivement, lorsque nous avions posé plus
haut:
(34.53)
Cela supposait implicitement
que l'équation des gaz parfaits était déjà connue
(…).
Cette approche de la cinétique
des gaz est intéressante car utile en astrophysique. Cependant,
ce n'est de loin pas la plus simple dans un cadre scolaire et
pédagogiquement.
Nous nous proposerons de revenir sur ces mêmes résultats
via les concepts de pression et de température cinétique
une fois l'équation de Van der Waals déterminée.
En 1875, le savant néerlandais J.D. Van der Waals (1837-1923)
essaya donc de remplacer l'équation des gaz parfaits par
une relation qui tiendrait compte des forces intermoléculaires
et de la taille des molécules. La première correction, et
la plus évidente, à l'équation
des gaz parfaits:
(34.54)
est de soustraire le volume des molécules de gaz du volume V.
Nous pouvons le faire logiquement en remplaçant V par V-Nb où b est
une constante très faible représentant bien évidemment le volume
moyen par molécule (il existe des tables pour cela). Donc:
(34.55)
où le terme est
communément appelé le "covolume".
Pour tenir compte des forces intermoléculaires que nous
avons négligées précédemment, nous
pouvons tenter une approche approximative en sachant déjà que
la force d'attraction de chaque molécule se
fera sur N-1 molécules. Par conséquent, le
numérateur de
la force d'attraction contiendra (par la somme de tous les termes)
trivialement si le gaz est isotrope et homogène un terme du type
N(N-1) pour
l'influence de toutes les molécules entre elles ce qui si N est
très grand peut être approximé par .
Nous savons également qu'au numérateur, il y aura
un terme de masse pour chaque particule. Si nous connaissons N/V alors
il ne reste plus qu'à connaître la densité massique du gaz
(mais ce n'est pas une variable extensive donc nous éviterons
de la faire apparaître explicitement). Ainsi, le terme peut
s'écrire directement
En suivant ce raisonnement, Van der Waals ajouta au terme de
droite de l'équation ci-dessus un terme négatif proportionnel à la
quantité .
La présence de ce terme se traduit par un abaissement de la pression
au fur et à mesure que croit la densité du gaz. La relation modifiée
est ainsi:
(34.56)
où a est une constante de proportionnalité. Nous pouvons
réécrire cette relation sous la forme:
(34.57)
qui est appelée "équation
d'état de Van der Waals" ou encore "équation
de gaz réels de Van der Waals" (on retrouve dans
la littérature plusieurs manières équivalentes d'écrire cette
dernière relation). Elle est une excellente description de l'équation
d'état
dans un large domaine des variables P,V,T,
les valeurs a et b étant caractéristiques
de chaque gaz. Les constantes a et b sont déterminées
expérimentalement
comme nous en avons déjà fait mention.
Nous pouvons représenter un l'équation de Van der
Waals dans un diagrmme P-V (donc à température
constante). Dont voici un exemple avec le CO2 (gaz carbonique/dioxyde
de carbone):
Figure: 34.5 - Diagramme P-V de Van der Waals
Ce qui correspond à:
(34.58)
La figure du bas montre le case général. On peut
passer de l'état F (vapeur) à l'état I (liquide)
en suivant un chemin passant per les états A et E (palier
de liquéfaction), on observe alors une transition
de phase. Si on suit un autre chemin, par exemple
en utilisant l'isotherme GH (T >Tk,
chemin rouge), il n'y a pas de palier de liquéfaction, on
passe de manière continue de l'état gazeux à l'état
liquide:
Figure: 34.6 - Diagramme P-V de Van der Waals générique
L'équation de Van der Waals peut être mise sous forme d'un
développement
du type Viriel en utilisant un développement de Taylor-Maclaurin
(cf. chapitre sur les Suites et Séries):
(34.59)
ou en réorganisant les termes:
(34.60)
Remarquons qu'il existe une température pour laquelle est
nulle. Nous l'appelons "température de Boyle" du gaz:
c'est la température à laquelle le gaz réel ressemble à un gaz
parfait. Il est très délicat d'obtenir ces paramètres expérimentalement.
PRESSION CINÉTIQUE
Recherchons le nombre de molécules d'un gaz parfait toutes supposées
animées d'une vitesse égale v qui viennent frapper une surface S pendant
une durée dt.
Si le gaz étudié est dans un état d'équilibre thermodynamique,
cela se traduira par l'homogénéité des variables intensives (hypothèse
du chaos moléculaire).
Il s'ensuit que la densité des particules est constante:
(34.61)
Si nous admettons que les molécules sont en mouvement, nous supposerons
qu'il y a isotropie des vitesses. En d'autres termes, puisque les
vitesses peuvent vectoriellement être décrites dans un système
de 3 axes orthogonaux (trois dimensions spatiales), il y a 6 directions
possibles primaires au total (2 directions par axe: en avant,
en arrière...).
Cela se traduit par l'équivalence entre les différentes directions.
Il y a:
(34.62)
particules ayant une vitesse v selon l'une des directions
primaires.
Donc pendant une durée dt, la surface S de
la paroi n'est percutée que par une partie des molécules
contenues dans le volume .
En effet, seul 1/6 des molécules contenues dans ce volume
se dirigent effectivement vers la surface S.

Figure: 34.7 - Une des parois de l'enceinte
Le nombre de molécules qui viennent heurter la paroi pendant
la durée dt est donc:
(34.63)
Étudions maintenant la dynamique du choc d'une particule
sur la paroi:
La particule de masse m qui arrive sur la paroi avec la
vitesse repart
avec une vitesse si
le choc est parfaitement élastique.
La variation de la quantité de mouvement de la particule
est donc:
(34.64)
En vertu de la conservation de la quantité de mouvement,
cette quantité de mouvement est transférée à la
paroi: la variation
de la quantité de mouvement subie par la paroi est l'opposé de
celle de la particule:
(34.65)
La variation totale de la quantité de mouvement de toutes les
particules qui viennent frapper la paroi pendant la durée dt vaut
alors en module:
(34.66)
En appliquant le principe fondamental de la dynamique, nous pouvons
passer à la force subie par la paroi pendant la percussion de ces
molécules:
(34.67)
donc:
(34.68)
Or par définition de la pression et en prenant le module:
(34.69)
nous avons alors la "pression
cinétique" donnée
par:
(34.70)
La pression cinétique est donc la traduction de la fréquence
des chocs sur la paroi. Plus les molécules sont nombreuses
(terme en )
et rapides (terme en v), plus le nombre de chocs augmente.
Cela est conforme à l'expérience et à l'intuition.
TEMPÉRATURE CINÉTIQUE
En remplaçant par
le quotient N/V, l'équation précédente
peut se mettre sous la forme:
(34.71)
Si nous l'identifions avec l'équation d'état des gaz parfaits
vue plus haut:
(34.72)
il vient:
(34.73)
Or la quantité de matière n est égale au rapport du nombre
de particules sur le nombre d'Avogadro:
(34.74)
ce qui permet de définir la "température cinétique" par:
(34.75)
Nous pouvons alors introduire une constante qui
nous est déjà connue appelée par Max Planck "constante
de Boltzmann" et telle que:
(34.76)
Remarque: Nous avions déjà fait mention de cette relation
lors de notre présentation des constantes universelles dans le
chapitre traitant des Principes de la mécanique.
L'expression de température cinétique prend alors
la forme:
(34.77)
Cette relation montre que la température cinétique
est le reflet de l'énergie cinétique des particules
(dont la température est en fait une mesure de la a vitesse des
molécules). D'une façon
imagée,
c'est l'image de la violence des chocs. On comprend aussi alors
mieux
l'origine de la définition de la température absolue
(sinon quoi la vitesse devrait être un nombre complexe) et
l'arguement comme quoi tout est immobile au zéro absolu.
Ainsi, l'énergie d'un gaz parfait se réduit à la
somme des énergies
cinétiques des particules qui le constituent:
(34.78)
Les atomes d'un gaz parfait monoatomique sont assimilables à des
points matériels. Leur énergie cinétique est
une énergie cinétique
de translation dont la valeur moyenne, par atome, s'écrit:
(34.79)
Dans l'espace des vitesses, toutes les directions sont équivalentes:
il y a isotropie de la distribution des vitesses. En coordonnées
cartésiennes, il vient:
(34.80)
et par suite de l'isotropie:
(34.81)
d'où:
(34.82)
ainsi, l'énergie cinétique moyenne par degré de liberté de translation
est égale à:
(34.83)
Le lecteur remarquera bien évidemment que nous obtenons ici les
mêmes résultats et conclusions que lors de notre étude du théorème
du Viriel à la différence que l'approche est ici plus simple et
donc plus didactique.
LOI DE DALTON ET D'AMAGAT
Considérons un mélange de deux gaz parfaits dans un volume V imposé constant à température T imposée
constante. Nous pouvons écrire pour chacun des gaz:
(34.84)
où sont
les "pressions partielles". L'ensemble du mélange
s'écrira:
(34.85)
Or:
(34.86)
et donc:
(34.87)
Donc:
(34.88)
La pression d'un mélange de deux gaz parfaits est la somme des
pressions partielles, il s'agit de la "loi
de Dalton".
Remarque: Nous avions mentionné dans
le chapitre de Thermodynamique, que la pression était une variable
intensive et donc non additive. Mais cela n'est pas le cas dans
la situation de gaz parfaits lorsque le volume est forcé comme étant
constant.
Ainsi, la pression partielle d'un gaz dans un mélange est égale
au produit de la pression totale du mélange par le pourcentage
du gaz considéré dans le mélange.
Nous pouvons faire le même raisonnement à pression P et température
T imposés comme constants. Nous avons alors:
(34.89)
d'où:
(34.90)
Le volume d'un mélange de deux gaz parfaits est la somme des
volumes partiels, il s'agit de la "loi
de d'Amagat".
LIBRE PARCOURS MOYEN
Nous allons voir maintenant un cas d'études très intéressant
des gaz qui permet de mettre au clair beaucoup d'incompréhensions
dans la vie de tous les jours (fumée dans les restaurants,
chaleurs près d'un radiateur, ...). Cependant, les phénomènes
sont en réalité plus
complexes il faut aussi prendre en compte la diffusion, la convection,
etc.
Considérons une molécule, qui se déplace à la
vitesse moyenne .
Sa sphère d'influence 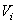 balaie
alors, pendant l'unité de temps de son déplacement,
un volume donné par: balaie
alors, pendant l'unité de temps de son déplacement,
un volume donné par:
(34.91)
Remarque: Dans le cas où l'on
considère un atome ou une molécule
comme une sphère d'influence, on parle souvent de "volume
de Van der Waals" et du "rayon
de Van der Waals" associé.
Si l'unité de volume renferme n molécules
(n a donc les unités d'une densité volumique),
le nombre de chocs pendant l'unité de
temps dans cette même
unité de volume sera alors de:
(34.92)
si les autres sphères d'influence étaient immobiles...
Donc pour tenir compte du mouvement des autres sphères d'influence,
considérons
la figure
ci-dessous avec trois scénarios simplistes:
Figure: 34.8 - 3 scénarios de collisions
De gauche à droite nous avons:
1. La vitesse relative des molécules est
2. La vitesse relative est nulle
3. La vitesse relative vaut (Pythagore)
Les deux premiers cas sont quand même un peu extrêmes... Le troisième
sera considéré comme représentant une moyenne et peut servir
de nouvelle base au calcul précédent.
Ainsi, en utilisant la vitesse relative du dernier scénario,
le nombre de chocs pendant l'unité de temps dans l'unité
de volume devient:
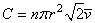 (34.93)
(34.93)
Ainsi, entre deux chocs, une molécule parcourt une distance
moyenne:
(34.94)
qu'il est d'usage de noter:
(34.95)
C'est donc l'expression du libre parcours moyen en fonction de
la densité moléculaire n (et non du nombre
de moles!!!) et du rayon r de
la sphère
d'influence, paramètre intrinsèque du gaz considéré.
Compte tenu de la relation:
(34.96)
où n est toujours la densité moléculaire
(et non le nombre de moles!!!) nous obtenons:
(34.97)
Une application numérique donne pour l'élément
aux conditions normales de température et de pression
un libre parcours moyen qui vaut pour la majorité des molécules
courantes plusieurs milliers de fois le diamètre
d'une molécule de taille standard (le libre parcours moyen
est donc de l'ordre du micromètre).
En utilisant la relation de la vitesse moyenne la plus probable
dans le cadre de l'hypothèse d'une distribution de Maxwell des
vitesses (cf. chapitre de Mécanique Statistique) nous avons:
(34.98)
pour une molécule de masse molaire de 30 [g] à température
normale. Ce qui donne un nombre de collisions pour une mole de
molécules:
(34.99)
Cette fréquence élevée de chocs explique,
dans des conditions normales de température et de pression,
la rapidité avec laquelle
l'équilibre statistique s'établit au sein d'un gaz.
À la température ambiante et pour un vide de ,
nous obtenons avec les mêmes valeurs: .
Les dimensions des récipients contenant les gaz étant
toujours inférieures à cet ordre de grandeur, il apparaît
que lorsque le vide est réalisé dans une enceinte,
les chocs intermoléculaires
sont négligeables vis-à-vis des chocs molécules-parois.
PLASMAS
Nous définissons
le "plasma" comme un état
de la matière dans lequel
certaines liaisons
électroniques ont été rompues, provoquant
l'apparition d'électrons
libres, chargés négativement et d'ions, chargés
positivement. Les gaz faiblement ionisés appelés "plasmas" par
abus de langage, possèdent les mêmes propriétés
mécaniques
(écoulements,
ondes acoustiques, etc.) que les gaz neutres, en revanche leurs
propriétés électromagnétiques
(conductivité électrique, indice
de réfraction) en diffèrent par suite de la présence
d'électrons
libres en leur sein.
Remarque: Le plasma est aussi nommé "quatrième
état de la matière" (après les états
solide, liquide et gazeux et avant le cinquième état
de la matière: le condensat de Bose-Einstein).
Dans leur
état normal, les gaz sont des isolants électriques. Cela tient
au fait qu'ils ne contiennent pas de particules chargées libres,
mais seulement des molécules neutres. Cependant, si nous leur
appliquons des champs électriques assez intenses, ils deviennent
conducteurs. Les phénomènes complexes qui se produisent alors
portent le nom de décharges dans les gaz et sont dus à l'apparition
d'électrons et d'ions libres.
Le résultat
d'une décharge dans un gaz est donc la production d'un
gaz ionisé
contenant par exemple une densité moyenne de 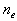 électrons,
ions positifs et
neutres (atomes ou molécules). En général,
le gaz est macroscopiquement neutre. Nous avons alors:
électrons,
ions positifs et
neutres (atomes ou molécules). En général,
le gaz est macroscopiquement neutre. Nous avons alors:
(34.100)
ou autrement exprimée, la neutralité s'écrit
aussi:
(34.101)
Cette neutralité
est la conséquence des forces électrostatiques très intenses qui
apparaissent dès que l'on a .
La densité de particules est donc la première grandeur
fondamentale.
Remarque: La neutralité n'est que globale. À une échelle plus fine, les
électrons, plus mobiles que les ions, forment un nuage autour de chaque
ion.
Le "degré
d'ionisation" d'un gaz est défini par le rapport:
(34.102)
où
est la densité de particules
neutres et n celle des électrons (ou des ions
positifs). La valeur du degré d'ionisation dans les
divers types de gaz ionisés
varie en pratique depuis des valeurs très faibles, de l'ordre
de
, par exemple, jusqu'à 1.
La deuxième
grandeur fondamentale est la température. Lorsque l'on
chauffe un gaz à une température T suffisamment élevée
( de l'ordre de
), l'énergie moyenne (voir théorème du Viriel):
(34.103) de translation
de ses molécules peut devenir du même ordre que leur énergie d'ionisation
Ei. Dans ces conditions, lorsque deux molécules
entrent en collision, il peut y avoir ionisation de l'une d'entre
elles. Si le gaz
est en équilibre thermodynamique, l'ionisation par collision est
contrebalancée par des processus de recombinaison entre électrons
et ions et il en résulte que les trois variables ne sont pas indépendantes: l'ionisation est déterminée
par la pression et la température, nous disons alors que le gaz
est en "état d'équilibre d'ionisation
thermique".
À des températures
plus élevées, les atomes du gaz peuvent d'ailleurs
s'ioniser plusieurs fois. Dans de nombreux cas, l'ionisation
est due à un champ électrique
extérieur, et le gaz n'est pas en équilibre thermodynamique.
Il atteindra souvent un état stationnaire que l'on pourra
caractériser
par les paramètres
(température des électrons),
(température des ions) et
(température des molécules).
Les trois
températures ainsi introduites sont définies par la condition
que représente
l'énergie cinétique moyenne des particules d'espèce a,
dans un repère où elles ont une vitesse moyenne nulle. L'écart
entre
,
et
peut être important: par exemple, dans un tube à décharges
typique, nous pourrons avoir:
et 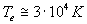 . La forte valeur de
est due à l'action du champ électrique sur les électrons,
et l'ionisation est alors produite par les collisions de ces électrons
chauds sur les molécules neutres du gaz.
. La forte valeur de
est due à l'action du champ électrique sur les électrons,
et l'ionisation est alors produite par les collisions de ces électrons
chauds sur les molécules neutres du gaz.
En conclusion
il n'y a que deux grandeurs de base permettant de caractériser
un plasma: la densité et la température électronique.
Nous allons maintenant nous pencher sur deux autres grandeurs
importantes
mais non fondamentales dans le sens où elles s'expriment à partir
de la densité et de la température.
FRÉQUENCE PLASMA
Si dans
un plasma initialement neutre, nous produisons une perturbation
locale sous la forme d'un excès de charge électrique positive
ou négative, celui-ci va tendre à revenir vers l'état d'équilibre
de neutralité. Cependant, nous pouvons voir facilement que la
perturbation initiale engendre en général une oscillation pendulaire
non amortie du plasma autour de son état d'équilibre. Considérons
par exemple la situation représentée sur la figure ci-dessous.
Figure: 34.9 - Oscillation électronique du plasma
À l'instant
initial la région au centre contient un déficit d'électrons et
la région tout autour un excès d'électrons. Cela produit un champ
électrique tendant à créer un mouvement des électrons dans le
sens des flèches. Dans ce mouvement, ceux-ci acquerront une certaine
énergie cinétique et ils pourront, au bout d'un certain temps,
dépasser la position d'équilibre. Un trop grand nombre d'électrons
ayant quitté la région externe, il y aura un défaut d'électrons
dans cette région et un champ électrique tendant à les ramener
vers elle. Au bout d'un certain temps, la situation initiale est
reconstituée et le cycle recommence. Les vibrations ainsi produites
sont appelées oscillations de plasma électroniques. Nous pouvons
étudier quantitativement ce problème en posant les équations générales
d'une oscillation de charge électronique et moyennant les hypothèses
simplificatrices suivantes:
H1.
Les ions sont supposés immobiles étant donné qu'ils
sont beaucoup plus lourds que les électrons, et leur quantité
égale à
H2.
L'agitation thermique est négligeable
H3.
Les collisions sont négligeables (nous parlons alors de
modèle à "transport
libre")
H4.
Les oscillations sont de faible amplitude H5.
Il n'y a pas de champ électrique ou magnétique imposé par
des sources extérieures
Maintenant,
rappelons que nous avons démontré dans le chapitre
d'Électrodynamique que (équation de conservation
de la charge):
(34.104)
et dans le chapitre d'Électrocinétique que:
(34.105)
Dès lors, en adoptant les notations susmentionnées,
il vient localement:
(34.106)
relation qui constitue "l'équation hydrodynamique
des électrons".
Remarque: Un plasma est certes en théorie globalement
neutre, mais nous pouvons avoir en théorie localement un
volume non neutre. C'est cette hypothèse qui nous permet
de poser que la divergence du courant n'est pas nulle!
Rappelons
maintenant la force de Coulomb (cf.
chapitre d'Électrostatique):
(34.107)
où nous avons donc clairement négligé le
terme de pression cinétique
et le terme de collision (hypothèses 2 et 3) et négligé le
champ magnétique
lié à l'oscillation.
Nous pouvons simplifier ces équations
en utilisant l'hypothèse 4 sous la forme:
(34.108) où
est une petite perturbation.
Supposons de plus que les quantités
variables varient à la pulsation 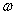 ,
nous pouvons donc écrire: ,
nous pouvons donc écrire:
(34.109)
Dès lors, l'équation hydrodynamique
des électrons devient:
(34.110) Soit au final:
(34.111)
De l'expression de la force de Coulomb nous déduisons également:
(34.112)
d'où nous tirons:
(34.113)
Mais nous
avons d'autre part la loi de Gauss (cf.
chapitre d'Électrodynamique):
(34.114)
en effet
compte tenu de la condition de neutralité du plasma non
perturbé,
nous avons:
(34.115)
Donc:
(34.116)
De la relation démontrée précédemment:
(34.117)
en remplaçant
dans la relation suivante (aussi démontrée précédemment):
(34.118) nous avons:
(34.119) Finalement
en remplaçant cette dernière expression dans la loi de Gauss,
nous tirons:
(34.120)
Mais dans
les oscillations de charges d'espace nous avons par définition
:
(34.121)
Ce qui nous amène à:
(34.122)
Finalement, nous avons la "fréquence
plasma" ou encore "fréquence
de Langmuir" donnée par:
(34.123)
En physique,
la fréquence plasma est ainsi la fréquence caractéristique
des ondes de plasma, c'est-à-dire des oscillations des
charges électriques présentes dans les milieux
conducteurs, comme le métal ou les plasmas. À l'image
de l'onde électromagnétique qui, quantifiée,
est décrite par des photons, cette onde de plasma est
quantifiée en "plasmons".
Les oscillations
des charges électriques peuvent être comprises
grâce au raisonnement suivant: si les électrons
d'une zone du plasma sont déplacés, alors les
ions de cette zone, n'ayant que peu bougé du fait de
leur masse importante, vont exercer sur ces électrons
une force de Coulomb attractive. Ceux-ci vont donc revenir
vers leur position initiale, et ainsi de suite...

- Mécanique des milieux
continus,
G. Duvaut, Éditions Dunod, ISBN10:
2100039326 (292 pages) - Imprimé en
1998
- Physique des plasmas (volume 1),
J.-L. Delcroix + A. Bers, Éditions EDP Sciences, ISBN10:
2868833683 (374 pages) - Imprimé en 1994
- Introduction to Food Engineering, Éditions
Elsevier, R. Paul Singh + Dennis R. Heldman,
ISBN10: 0123985307 (892 pages) - Imprimé en
2013
- Notions de Mécanique des
fluides, Centre de Publication
Universitaire, Riadh Ben Hamouda, ISBN13: 9789973374943
(135 pages) - Imprimé en
2008
|