News :: Erreur :: Visiteurs :: ClearType :: Imprimer ::

PRINCIPES | MÉCANIQUE ANALYTIQUE | MÉCANIQUE CLASSIQUE
MÉCANIQUE ONDULATOIRE | MÉCANIQUE STATISTIQUE | THERMODYNAMIQUE
MÉCANIQUE DES MILIEUX CONTINUS

Dernière mise à jour de ce chapitre: 2015-09-06 16:38:32 | {oUUID 1.814}
Version: 3.1 Révision 7 | Rédacteur: Vincent ISOZ  | Avancement: ~90%
vues depuis le 2012-01-01: 4'890

LISTE DES SUJETS TRAITÉS SUR CETTE PAGE

LIQUIDES (FLUIDES)

Les fluides usuels sont de deux types: les liquides et les gaz (les solides sont aussi parfois considérés comme des fluides... ce n'est qu'une question d'opinion...). Étymologiquement, un fluide est susceptible de s'écouler. Le liquide adopte la forme du récipient qui le contient tout en conservant un volume propre à peu près invariable. Le gaz n'a pas de volume propre: il envahit uniformément (mécanique statistique de Boltzmann) le récipient dans lequel il est maintenu. Une atmosphère en constitue un cas spécial, du fait qu'elle est maintenue par la gravité à la périphérie d'un astre, ce qui exclut l'uniformité de la densité ou pression.

La distinction entre liquide et gaz est subtile. Nous pouvons cependant dire que le volume propre des liquides manifeste l'existence d'une cohésion liée à une densité assez grande (liaisons de Van der Waals); cette cohésion disparaît avec le volume propre chez les gaz.

Si nous comparons les fluides avec les solides, la première remarque qui s'impose concerne l'isotropie (les propriétés sont les mêmes dans toutes les directions spatiales) des fluides usuels qui est toujours réalisée (si nous n'agissons pas sur le fluide en tout cas!).

Nous allons aborder la théorie de la mécanique des fluides en difficulté croissante et par redondance. D'abord, il va être démontré que les propriétés d'un fluide statique sont isotropes (théorème de Pascal). À l'aide de ce résultat, il va être plus simple de comprendre le théorème de Bernoulli qui va nous permettre, entre autres, de définir le concept de "pression hydrostatique". Ensuite, nous construirons un modèle très important de la dynamique des fluides, connu sous le nom de "équations de Navier-Stokes", que l'on retrouve dans tous les domaines possibles (astrophysique, mécanique quantique, météorologie,..). Ce modèle de dynamique des fluides est conséquent en développements théoriques et résultats expérimentaux et peut être considéré comme un terrain difficile. Cependant, pour faciliter la lecture, nous avons choisi de ne pas aborder celui-ci directement par usage du calcul tensoriel. Nous avons ainsi fait en sorte que les variables tensorielles apparaissent d'elles-mêmes d'écoulant des résultats simples de l'analyse vectorielle que nous obtiendrons. Une fois les équations de Navier-Stokes déterminées et démontrées, nous verrons que nous pouvons retrouver l'expression du théorème de Bernoulli à partir de ces mêmes équations.

La dynamique des fluides, ou "hydrodynamique", est de loin, le domaine de la mécanique classique le moins aisé en ce qui concerne la description et la prédiction. C'est pourquoi le théorème de Bernoulli s'utilise fréquemment, non pour expliquer en détail le comportement d'un fluide, mais pour en faire une description qualitative.

THÉORÈME DE PASCAL

Le résultat qui va suivre est de la plus haute importance pour comprendre l'ensemble de la mécanique des fluides. Il faut donc prendre le temps de comprendre!

Figure: 34.1 - Tétraèdre régulier élémentaire pour faire émerger le théorème de Pascal

Si nous considérons les forces s'exerçant, en l'absence de mouvement, sur un  tétraèdre élémentaire OABC de volume élémentaire V, il est toujours possible d'adopter un volume suffisamment petit pour avoir une pression uniforme s'exerçant sur les faces du tétraèdre.

Soient , les pressions de réaction du fluide dues aux contraintes extérieures sollicitant les faces respectives OBC, OAB, OAC et ABC de surface . Soient également les cosinus directeurs (cf. chapitre de Calcul Vectoriel) du vecteur unitaire  normal à la surface ABC.

Le système étant en équilibre, la résultante des forces de réaction du système est nulle. Nous avons donc les équations suivantes résultant de la projection suivant les trois axes de coordonnées:

  (34.1)

Par simplification élémentaire, il vient:

  (34.2)

Nous obtenons alors la relation suivante:

  (34.3)

Conclusion importante: En un point quelconque d'un fluide, la pression est indépendante de la direction de la normale  à la surface élémentaire sur laquelle elle s'exerce.

Par le principe de l'action et de réaction de Newton, nous sommes amenés à énoncer le "théorème de Pascal" ou "principe de Pascal": Les fluides incompressibles (en équilibre) transmettent intégralement et dans toutes les directions, les pressions qui leur sont appliquées.

Ce théorème est fondamental aussi bien en mécanique des fluides qu'en mécanique des gaz et les implications pratiques sont énormes. Ce théorème explique entre autres le fameux "paradoxe hydrostatique" comme quoi la pression d'un liquide sur le fond d'un récipient est indépendante de sa forme, et aussi de la surface du fond mais ne dépend seulement de la hauteur d'eau dans le récipient. Ce théorème est à la base de la conception de nombreuses machines hydrauliques!

Voyons-en une illustration très claire. Considérons le schéma suivant (nous avons fait un exemple en U bien que la majorité des symtèmes hydrauliques soient linéaires):

Figure: 34.2 - Exemple typique de machine hydraulique (élévateur, cric hydraulique)

Que se passe-t-il exactement? Eh bien sur la partie gauche, nous avons la force qui crée une pression:

  (34.4)

et de par le principe de Pascal, nous devons retrouver la même pression de l'autre côté tel que:

  (34.5)

Il s'ensuit immédiatement la relation très importante dans la pratique:

  (34.6)

Nous avons donc une démultiplicateur de force! Attention! Le principe de la machine hydraulique est donc un fantastique démultiplicateur de force mais en aucun cas il démultiplie le travail! Donc de par le principe de conservation de l'énergie, nous avons:

  (34.7)

et il vient alors:

  (34.8)

Ainsi, entre contrepartie de la démultiplication de force, de par la conservation de l'énergie, la force primaire devra parcourir une plus grande distance.

VISCOSITÉ

En mécanique des fluides, il est utile de considérer plusieurs types fluides ayant des caractéristiques qui les différencient. Ceci s'avère particulièrement pratique pour les simulations tout en restant conforme à l'observation expérimentale (cf. chapitre de Génie Météo Et Marin).

Nous définissons la "viscosité" par les forces internes s'opposant au déplacement des diverses couches composant le fluide.  Nous distinguons la "viscosité dynamique"  et la "viscosité cinématique" .

1. La viscosité dynamique:

  (34.9)

avec  étant le coefficient de viscosité dynamique (l'unité étant le Poiseuille [PI]), dF la variation de la force de frottement entre deux couches infiniment voisines,  variation de la vitesse par la distance entre deux couches infiniment voisines  et dS étant la surface considérée .

Conclusion: Le Poiseuille est la viscosité d'un fluide nécessitant 1 Newton pour faire glisser à la vitesse de 1 mètre par seconde, deux couches fluides de 1 mètre carré distantes de 1 mètre.

Remarque: Anciennement, l'unité employée était la "poise":

2. La viscosité cinématique est définie par:

  (34.10)

Une transformation de la définition de la viscosité dynamique donne (il faut se rappeler de cette relation pour plus tard!!):

  (34.11)

Soit:

  (34.12)

Par définition les fluides ayant les caractéristiques suivantes:

Figure: 34.3 - Caractéristiques de viscosité de différents fluides

sont nommés respectivement:

- (1) Fluides pseudo-plastiques
- (2) Fluides newtoniens (contraintes de cisaillement proportionnelles au gradient de vitesse)
- (3) Fluides dilatants

Il existe encore 3 autres types de fluides non représentés sur la figure et dont la viscosité est supposée nulle (cf. chapitre de Thermodynamique):

- (4) Fluides parfaits
- (5) Fluides semi-parfaits
- (6) Fluides réels

Les fluides non-newtoniens ont donc une déformation qui dépend de la force que nous leur appliquons. Le meilleur exemple est celui du sable mouillé en bord de mer: quand nous frappons le sable, il a la viscosité élevée d'un solide, alors que lorsque nous appuyons doucement dessus, il se comporte comme une pâte. Par ailleurs, certains fluides non-newtoniens ont des propriétés telles qu'il est possible pour un individu de courir dessus sans couler ou de couler en restant en position...

LOI DE POISEUILLE

En 1835 un médecin français, Jean Léonard Marie Poiseuille fit une série d'expériences soignées, pour déterminer comment un fluide visqueux s'écoule dans un tuyau étroit. Son but était de comprendre la dynamique de la circulation sanguine chez l'homme. Le plasma du sang se comporte comme un fluide newtonien, tandis que le sang entier ne l'est pas. Presque la moitié du volume normal du sang est faite de cellules assez grandes pour perturber l'écoulement laminaire, surtout quand elles entrent en contact avec les parois des vaisseaux, un phénomène qui prend de l'importance dans les capillaires très étroits. Néanmoins, l'analyse de Poiseuille s'applique à l'écoulement dans les veines et les plus grosses artères et elle a une grande valeur, bien qu'elle soit un peu simpliste.

Le résultat de Poiseuille peut être établi en considérant le fluide dans un tuyau comme formé de couches cylindriques orientées selon un axe x de rayon r concentriques qui se déplacent à des vitesses qui vont en décroissant à partir du centre (symétrie circulaire supposée).

Alors la relation définissant la viscosité s'écrit:

  (34.13)

Ce qui nous donne la force de viscosité sur le cylindre. La surface de contact de chaque couche cylindrique de longueur l est donnée par et donc:

  (34.14)

L'origine de l'accélération (in extenso de la force) ne peut se faire que par une différence de pression telle que:

  (34.15)

ce qui nous amène à écrire:

  (34.16)

En intégrant membre à membre, nous obtenons:

  (34.17)

Nous obtenons donc la fameuse "loi d'écoulement laminaire visqueux" découverte par le physicien français Jean-Louis-Marie Poiseuille en 1840:

  (34.18)

très utilisée en médecine pour calculer la vitesse d'écoulement du sang dans les veines, dans les installations hydrauliques (pour déterminer la pression nécessaire afin d'avoir un certain débit), dans les souffleries (pour la même raison que dans les installations hydrauliques).

La courbe représentative de la vitesse en fonction de r est une parabole dont le sommet se situe sur l'axe centre du cylindre (). Donc la vitesse est plus grande au centre que sur les bords (c'est intuitif). En dérivant cette dernière relation par rapport à r, on obtient immédiatement le gradient de vitesse en fonction de r (calcul utile dans la pratique).

Le "débit volumique" J (tantôt noté D dans les petites classes) transporté par une couche cylindrique entre r et r + dr est

  (34.19)

Ainsi, le débit total est:

  (34.20)

et nous obtenons la "loi de Poiseuille" pour le débit laminaire visqueux:

  (34.21)

Nous trouvons donc le résultat logique que le débit augmente avec le gradient de pression et le rayon du tube, et diminue avec la viscosité.

Nous trouvons par ailleurs une relation analogue à la loi d'Ohm (cf. chapitre d'Électrocinétique) où la différence de potentiel est donnée par la résistance multipliée par le courant alors que la différence de pression est donnée par la résistance visqueuse multipliée par le débit. Nous reviendrons également sur cette relation lorsque nous traiterons les pertes de charge dans les conduites.

THÉORÈME DE BERNOULLI

Quand nous discutons du mouvement d'un fluide, l'équation de continuité (cf. chapitre Thermodynamique), qui exprime la conservation de la masse (volumique) du fluide est une notion importante.

  (34.22)

Considérons cette équation dans le cas particulier qui nous intéresse ici un fluide non visqueux en écoulement laminaire se déplaçant à l'intérieur d'un tube de lignes de courants parallèles (le mouvement du fluide est de type irrotationnel - voir chapitre de Calcul Vectoriel), délimité par la surface :

Figure: 34.4 - Fluide non visqueux en écoulement laminaire d'un tube de lignes de courants parallèles

Nous sommes en régime stationnaire (l'aspect du mouvement est indépendant du temps) et la masse n'est ni apportée par une source ni enlevée par un puits à l'intérieur de la région considérée. Le volume de fluide qui traverse dans l'intervalle   correspond à un cylindre de base , de longueur  et donc de volume . La masse de fluide qui a traversé pendant le temps  est donc:

    (34.23)

De même:

    (34.24)

est la masse de fluide qui a traversé pendant le même intervalle de temps. Avec les hypothèses faites, l'équation de conservation de la masse exige que les deux masses soient les mêmes, ou exprimé autrement:  

  (34.25)

D'où:

  (34.26)

Ceci est la forme de l'équation de continuité dans le contexte qui nous intéresse. De plus, si le fluide est incompressible, la densité est partout la même et l'équation précédente se réduit à:

    (34.27)

Ainsi, le rapport des vitesses entrée/sortie dans une conduite tubuliare sera en général (frottements non pris en compte!):

  (34.28)

L'équation de continuité est connue indirectement de tous les enfants et adultes qui jouent avec ou utilisent un tuyau d'arrosage (le pouce sert de "convergent"):

Figure: 34.5 - Application de tous les jours de l'équation de continuité

Considérons maintenant une région dans un fluide où il y a un flux stationnaire comme l'indique la figure ci-dessous:

Figure: 34.6 - Agrandissement sur une région du fluide

Pendant un court intervalle de temps , le fluide qui, initialement, traversait a progressé jusqu'à une surface  à la distance  tandis que le fluide qui traversait se retrouve en  à une distance . Puisque le reste du volume entre les surfaces  et reste inchangé, nous allons porter notre attention sur les deux volumes (égaux) hachurés sur la figure.

Ces deux volumes sont égaux, car le fluide est incompressible et l'équation de continuité est valable. Soient  et  les forces exercées sur les surfaces  et  en raison de la pression existant dans le fluide. À cause de ces forces, le fluide produit ou reçoit du travail en déplaçant les deux volumes. En , la surface est poussée par le fluide et le travail exercé sur le fluide est  alors qu'en  le fluide pousse la surface et le travail effectué par le fluide est . Le travail total exercé sur le volume de fluide situé entre  et est donc:

  (34.29)

en appelant  et  les pressions respectives en  et  et en écrivant: 

  (34.30)

d'après la définition de la pression. Comme:

  (34.31)

d'après l'équation de continuité et l'hypothèse d'incompressibilité, nous pouvons écrire que:

  (34.32)

Le travail extérieur exercé sur le système change son énergie propre comme l'établit la thermodynamique (). Pour le volume de fluide considéré, l'énergie propre des volumes mise en évidence comprend l'énergie cinétique et l'énergie potentielle de gravitation. Le fluide entre   et  gagne de l'énergie dans le volume . Supposons que les deux volumes aient une masse égale m, de nouveau à cause de l'équation de continuité. Alors le gain net d'énergie est:

  (34.33)

Puisque nous avons déjà supposé le fluide incompressible, la densité  est la même partout et m peut être remplacé par  aux deux extrémités. D'où:

  (34.34)

En combinant cette relation avec  nous obtenons:

  (34.35)

ou: 

  (34.36)

Comme l'équation ci-dessus concerne des grandeurs prises en deux points arbitraires le long d'une ligne de courant, nous pouvons généraliser et écrire:

  (34.37)

Ce résultat, connu sous le nom de "théorème de Bernoulli", exprime la constance de la pression le long d'une ligne de courant dans un fluide incompressible, irrotationnel et non visqueux et où les forces volumiques extérieures dérivent d'une énergie potentielle (nous reviendrons là-dessus après avoir déterminé les équations de Navier-Stokes).

Signalons aussi une manière  élégante et simple de retrouver cette relation. La conservation de l'énergie nous donne le long d'une ligne de courant:

  (34.38)

avec respectivement et dans l'ordre la somme de l'énergie cinétique, de l'énergie potentielle et de l'énergie de pression. Soit:

  (34.39)

et si nous divisons tout cela par le volume, nous obtenons alors:

  (34.40)

voilà....

Considérons maintenant deux applications importantes du théorème de Bernoulli.

Si le fluide se déplace dans un plan horizontal, l'énergie potentielle de gravitation reste constante et l'équation de Bernoulli se réduit alors à:

  (34.41)

Donc, dans un tuyau horizontal fermé, la vitesse est d'autant plus grande que la pression est plus faible et réciproquement. Nous utilisons aussi cet effet pour participer à la poussée d'un avion du moins dans le cas d'essais en soufflerie dans une cylindre fermé (attention ce paramètre est mineur dans le cas d'un déplacement dans l'atmosphère qui est un volume ouvert, car ce n'est pas ce qui contribue le plus au vol d'un avion, c'est l'effet Magnus dont la démonstration sera donnée plus loin un jour...).

Figure: 34.7 - Illustration du profil d'une aide avec les pressions correspondantes

Le profil d'une aile est construit de telle sorte que l'air ait une vitesse plus grande au-dessus de la surface de l'aile qu'au-dessous, ce qui produit une pression plus forte au-dessous qu'au-dessus dans le cas d'un courant d'air dans un cylindre fermé (comme c'était le cas lors des premiers essais en soufflerie au début des années 1900!). Il en résulte donc une force résultante vers le haut. 

Autrement dit, une spécialiste dans l'aérodynamique (pour les avions) ou en hydrodynamique (pour les stabilisateurs de roulis des gros bateaux) dirait dans le cas d'essais en volume fermé:

- À l'extrados: Par effet de courbure, les particules d'air (d'eau) vont passer par une surface transversale plus faible dans le cylindre d'essai et par effet Venturi vont alors accélerer. Leur vitesse va donc d'abord s'accroître fortement pour diminuer ensuite afin de retrouver au bord de fuite la vitesse initiale de l'écoulement. Tout l'extrados est donc le siège d'une dépression locale généralisée.

- À l'intrados: Par effet de courbure, les particules d'air (d'eau) vont passer par une surface transversale plus grande dans le cylindre d'essai et par effet Venturi vont alors décélérer. Leur vitesse va donc diminuer fortement pour augmenter ensuite afin de retrouver au bord de fuit la vitesse initiale de l'écoulement. Tout l'intrados est donc le sièce d'une surpression locale généralisée.

La portance d'une aile en ce qui concerne sa géométre serait due en plus grande partie par la dépression sur l'extrados, et non à la surpression sur l'intrados. l'aile ne "repose" pas sur l'air, mais est aspiré par ce dernier vers le haut

C'est bien mieux ainsi non ?

Autre chose encore, si le fluide n'est pas en mouvement, nous avons l'équation de Bernoulli qui s'écrit:

  (34.42)

Il s'agit de "'équation de Laplace" en hydrostatique (utilisée dans les vases communicants).

THÉORÈME DE TORRICELLI

Le théorème de Torricelli permet de déterminer la vitesse d'écoulement d'un liquide. C'est un cas classique d'étude dans les petites écoles.

Considérons un volume fermé contenant un liquide de masse volumique et muni d'un orifice de surface , duquel le liquide coule vers l'extérieur. Nous voulons déterminer la vitesse d'écoulement du liquide de cet orifice.

Figure: 34.8 - Schéma de principe pour le thoèrme de Toricelli

Le volume est supposé être assez grand pour que ni le niveau du liquide, ni la pression P au-dessus de sa surface ne varient de façon appréciable pendant l'écoulement. Comme le tube d'échappement de liquide va de la région de la surface du liquide à l'orifice ouvert à l'air libre, nous avons . Un liquide coulant à l'air libre est à la pression atmosphérique, , car le liquide est entouré d'air libre et rien ne peut maintenir une différence de pression. D'après l'équation de Bernoulli, avec , nous trouvons sur une ligne de courant:

  (34.43)

d'où:

  (34.44)

De l'équation de continuité (), nous déduisons que si alors et est alors négligeable devant . Dans le cas particulier, mais fréquent, où le réservoir est ouvert à l'air libre (), la densité d'énergie de pression disparaît. Le fluide coule sous l'effet de la gravité, sans être poussé par une différence de pression. Nous trouvons alors (en multipliant par la surface de l'orifice, nous obtenons le débit):

  (34.45)

qui est indépendant des sections! Évidemment en utilisant cette dernière relation, dans le cas où sont donnés le débit et la surface de l'orifice nous pouvons en déduire la vitesse d'écoulement.

Cette relation constitue le "théorème de Torricelli". Chose curieuse, nous avons déjà vu cette relation dans le chapitre de MécaniqueCclassique pour la vitesse de chute libre d'un corps. Il en retourne l'observation faite par Torricelli: si le jet est dirigé directement vers le haut, il atteint presque le niveau de la surface du liquide dans le volume. La raison pour laquelle le jet n'atteint pas effectivement ce niveau est une certaine perte d'énergie à cause du frottement.

De ce résultat nous pouvons étudier un cas intéressant dans la pratique et souvent aussi utilisé dans les cours de modélisation numérique. Il s'agit de déterminer le temps pour qu'un réservoir du type suivant se vide:

Figure: 34.9 - Vidange verticale d'un réservoir

Nous partons donc du théorème de Toricelli dans le cas où l'orifice est beaucoup plus petit que la diamètre du réservoir (nous verrons après que sinon la vitesse n'est plus la même!):

  (34.46)

et le débit est alors trivialement:

  (34.47)

où le signe "-" est là pour indique que le réservoir se vide. Nous avons aussi le débit qui est défini par:

  (34.48)

et le volume V pouvant être exprimé par:

  (34.49)

Nous avons alors explicitement:

  (34.50)

Dans notre cas particulier, la surface ne dépend pas du z. Nous avons alors:

  (34.51)

Soit après réarrangement:

  (34.52)

Maintenant nous intégrons à gauche de H à 0 (H étant la hauteur initiale du fluide) et à droite de 0 à T. Nous avons alors:

  (34.53)

Soit après réarrangement nous en déduisons que le temps T de vidange est:

  (34.54)

et nous remarquons que si le rayon de l'orifice d'évauation est égal au rayon du cylindre on retombe sur l'expression du temps de chute libre d'une masse ponctuelle vu dans le chapitre de Mécanique Classique.

VASES COMMUNICANTS

Parlons un tout petit peu des vases communicants car l'air de rien, encore en ce début du 21^ème siècle, la majorité des immeubles ont un approvisionnement de l'eau courante basée sur ce principe (lacs de réserve en hauteur, sources en hauteur, châteaux d'eau) et de nombreuses personnes ont fait usage du principe des vases communicants pour siphonner un fluide d'un réservoir/récipient d'un autre au moins une fois dans leur vie.

Nous pouvons d'abord introduire le concept intuitivement en nous basant sur le constat expérimental des 4 vases communicants de la figure suivante avec un fluide non visqueux:

Figure: 34.10 -Photo du principe des vases communicants

nous constatons que les que le fluide se stabilise à la même hauteur pour les quatre vases quelle que soit leur forme!

Il en va de même pour un château d'eau (indispensable s'il s'agit de diminuer les coûts d'approvisionnement et si l'emplacement ne permet pas de jouer avec la topographie des lieux):

Figure: 34.11 - Application des vases communicants avec des châteaux d'eaux

Ainsi, si nous voulons au 4ème étage d'un immeuble avoir un débit minimal à un robinet donné, nous allons devoir appliquer le théorème de Torricelli pour savoir à combien de mètres h au-dessus du niveau du robinet soit de trouver le niveau d'eau du château d'eau.

Nous avions obtenu plus haut:

  (34.55)

Donc:

  (34.56)

Soit en utilisant la définition du débit:

  (34.57)

Où D est débit à assurer en mètres cubes par seconde et S, la section à travers laquelle nous devons assurer ce même débit? Ainsi, un débit de 0.05 litre par seconde (typique d'un robinet de cuisine ou de salle de bain) à travers une section ayant un rayon de 0.5 centimètres donnera:

  (34.58)

Valeur qui ne prend donc pas en compte les pertes de charges dans la conduite!

EFFET VENTURI

Certaines applications pratiques de la mécanique des fluides résultent de l'interdépendance de la pression et la vitesse. Il y a une catégorie de situations dans lesquelles la variation d'énergie potentielle gravitationnelle est négligeable. L'équation de Bernoulli relie alors la différence de pression à la différence d'énergie cinétique donc la variation du carré de la vitesse.

Nous considérons un fluide incompressible (!), non visqueux et de masse volumique. Le fluide s'écoule en régime permanent dans une canalisation cylindrique de rayon  et de section  suivie par un tube cylindrique de rayon  et de section et qui reprend ensuite la géométrie initiale de rayon  et de section (il s'agit typiquement d'un racordement qu'il est d'usage d'appeler "tube de Venturi"). Le raccordement est fait par une canalisation cylindrique assez longue pour que l'on reste en régime laminaire:

Figure: 34.12 - Tube de Venturi

Nous savons (équation de continuité) que:

  (34.59)

qui veut dire, comme nous l'avons vu, qu'une diminution de la section traversée par le fluide se traduit par une augmentation de sa vitesse.

Dans toute situation où le flux entrant est environ au même niveau que le rétrécissement , l'équation de Bernoulli s'emploie pour exprimer la différence de pression:

  (34.60)

devient:

  (34.61)

Utilisant l'équation de continuité, pour éliminer (arbitrairement) , nous obtenons:

  (34.62)

Nous pouvons aussi écrire en utilisant l'équation fondamentale de l'hydrostatique:

  (34.63)

Comme le second membre de la relation est positif et : il y a donc une chute de pression dans la région étroite. En arrivant à la région divergente à nouveau en , la pression du fluide augmente de nouveau et la vitesse reprend sa valeur initiale. Cette diminution de la pression qui accompagne l'augmentation de la vitesse est appelée "effet Bernoulli" ou "effet Venturi".

Ainsi, la vitesse du fluide augmente dans un goulot d'étranglement pour satisfaire l'équation de continuité (conservation du flux/masse) et le fait qu'il soit incompressible (sinon il y aurait une sorte de bouchon...).

De la dernière relation, nous tirons trivialement une égalité très utile dans la pratique:

  (34.64)

qu'il suffit de multiplier par la surface pour avoir le débit dans le racordement. Évidemment nous avons de même:

  (34.65)

TUBE DE PITOT

Le tube de Pitot permet la mesure de la vitesse d'écoulement d'un fluide/gaz subsonique parfait (supposé en écoulement permanent). Le tube de Pitot le plus utilisé en aéronautique consiste à pratiquer dans un tube, un orifice de prise de pression en A et en B:

Figure: 34.13 - Tube de Pitot horizontal

Le point A est un point d'arrêt, car la vitesse y est nulle (il n'y a pas d'écoulement dans l'orifice, c'est juste une prise de pression). Loin de l'obstacle (le tube de Pitot) l'écoulement est supposé uniforme de vitesse v et de pression  .

En A (point d'arrêt), en utilisant la relation de Bernoulli le long de la ligne de courant et en considérant la variation de hauteur entre A et B négligeable, la pression vaut:

  (34.66)

Nous avons donc:

  (34.67)

Donc pour les avions à partir de la différence d'une mesure de pression et de la connaissance de la densité du gaz, il est possible de connaître la vitesse! En multiplisant par la section du conduit nous avons aussi alors le débit correspondant.

Il existe une autre variante du tube de Pitot plus utilisé dans le domaine industriel dont voici le schéma:

Figure: 34.14 - Tube de Pitot vertical

Nous appliquons donc aussi le théorème de Bernoulli sur l'axe de la conduite. Nous y avons alors (nous détaillons les développements un peu plus que dans l'exemple précédent):

  (34.68)

or , et donc:

  (34.69)

Mais nous avons aussi en utilisant le théorème fondament de l'hydrostatique:

  (34.70)

Nous avons alors:

  (34.71)

PERTE DE CHARGE (PRESSION)

Lorsque, dans un écoulement d'un fluide parfait, il n'y a aucune machine (ni pompe ni turbine) entre les points (1) et (2) d'une même ligne de courant, la relation de Bernoulli peut s'écrire sous la forme suivante:

  (34.72)

Lorsque le fluide traverse une machine hydraulique, il échange de l'énergie avec cette machine sous forme de travail pendant une durée donnée. La puissance P échangée est alors (cf. chapitre de Mécanique Classique):

  (34.73)

où par convention, si  l'énergie est reçue par le fluide (pompe) sinon, si  l'énergie est fournie par le fluide (turbine).

Si le débit-volume est , la relation de Bernoulli s'écrit alors logiquement:

  (34.74)

où:

  (34.75)

Un fluide parfait n'existe pas. Lors d'un écoulement dans une conduite, les forces de frottement dissipent une partie de l'énergie cinétique et potentielle ce qui se traduit par l'existence de pertes de charges dont il s'agit de tenir compte.

Considérons un écoulement cylindrique horizontal stationnaire et incompressible. Si nous appliquons la relation de Bernoulli entre l'entrée et la sortie, nous obtenons:

  (34.76)

Or, expérimentalement, nous observons qu'il faut imposer une pression plus importante en entrée pour entretenir le régime permanent. En effet, les forces de viscosité résistent à l'écoulement. Il faut donc imposer une suppression  que nous appelons "perte de charge en pression" et qui est due à l'existence de forces de frottements (viscosité) ou de pertes singulières (géométrie des circuits de distribution).

L'équation de Bernoulli généralisée s'écrit alors dans ce cas d'étude qui fait partie de l'ingénierie des procédés:

  (34.77)

Cette relation est souvent utilisée dans l'étude théorique (...) des problèmes de conduite.

Dans la pratique, la perte de charge est calculée à partir de la loi de Poiseuille que nous avons démontrée plus haut:

  (34.78)

où pour rappel J est la notation traditionnelle du débit volumique dans ce domaine particulier.

Ce qui est intéressant à observer avec la loi de Poiseulle dans le cas de l'analyse des pertes de charge c'est que le débit volumique est donc inversement proportionnel à la distance l de la conduite horizontale. Ainsi, la perte de charge et donc la pression à l'extrémité d'une conduite se calcule très facilement en réarrangement la relation ci-dessus:

  (34.79)

Donc évidemment la pression à l'extrimité d'une conduite est moins grande que la pression en amont.

ÉQUATIONS DE NAVIER-STOKES

Soit un parallélépipède élémentaire extrait d'un fluide statique à l'équilibre de dimensions dx, dy, dz représenté à la figure ci-dessous. La matière à l'équilibre composant le parallélépipède est en général soumise à des forces de volume dans toutes les directions (théorème de Pascal) dont les composantes sur les trois axes orthogonaux sont représentées sur la figure ci-dessous (ces forces peuvent être de nature gravitationnelles, électromagnétiques ou inertielles...).

Figure: 34.15 - Parallélépipède élémentaire extrait d'un fluide statique à l'équilibre

Nous pouvons, comme nous l'avons représenté ci-dessus, décomposer et translater l'ensemble des forces auxquelles est soumis le parallélépipède aux centres des faces de ce dernier. Nous représentons bien évidemment chacune des contraintes sur chacune des faces comme la somme des contraintes normales et tangentielles telles que nous l'avions fait pour l'étude des solides sous contrainte (selon les trois axes toujours, d'où la somme de trois composantes!).

Au total, nous nous retrouvons avec 18 composantes de contraintes normales et tangentielles:

  (34.80)

Nous cherchons à minimiser le nombre de composantes normales afin de déterminer quelles sont les contraintes suffisantes sur chacun des axes. Ainsi, nous poserons:

  (34.81)

Donc trois composantes suffisent pour connaître les forces de contraintes normales aux surfaces selon chaque axe.

Si nous effectuons la somme des moments de forces par rapport aux centres de gravité pour chaque axe de symétrie du parallélépipède (XX',YY',ZZ') il est évident que sur les 12 composantes tangentielles, 6 suffisent pour décrire l'ensemble du système.

Ainsi pour le plan XOY passant par le centre de gravité nous avons:

  (34.82)

Pour le plan XOZ:

  (34.83)

Pour le plan ZOY:

  (34.84)

Donc pour chaque plan (XOY, ZOY, ZOX), une composante suffit pour décrire l'ensemble de moments de forces.

Ainsi, par souci de simplification d'écriture, nous poserons (il est plus conforme de faire les développements avec des indices en minuscules):

et    (34.85)

Au total, cela nous fait donc 3 composantes tangentielles plus 3 composantes normales qui sont suffisantes et nécessaires pour décrire les contraintes sur le parallélépipède selon chaque axe du plan de symétrie de ce dernier:

  (34.86)

Nous pouvons obtenir les mêmes composantes d'équilibre en considérant cette fois un tétraèdre régulier élémentaire (extrait du cube) statique. Le but étant de démontrer que nous retrouvons bien les 6 composantes déterminées précédemment.

Figure: 34.16 - Tétraèdre régulier élémentaire extrait d'un fluide à l'équilibre

Pour connaître l'aire des faces OAC, OBC, OAB , nous multiplions la surface ABC (notée ci-après: S) par le cosinus de l'angle que forment les vecteurs   et .

Effectivement, soit les surfaces:

 et   (34.87)

Cependant, nous cherchons à exprimer les  en fonction de S. Le schéma ci-dessous (coupe du tétraèdre) devrait aider à comprendre le raisonnement:

  (34.88)

et donc:

  (34.89)

Finalement:

  (34.90)

Le rapport:

  (34.91)

d'où:

  (34.92)

Le principe d'analyse étant le même pour toutes les autres surfaces telles que:

  (34.93)

Nous écrirons donc:  

  (34.94)

tel que:

  (34.95)

Remarque: Nous pouvons facilement connaître les valeurs des  à l'aide de l'analyse vectorielle. Effectivement, le plan ABC étant d'équation:

  (34.96)

en simplifiant par :

  (34.97)

Le vecteur normal au plan étant bien:

  (34.98)

pour connaître les cosinus de l'angle du vecteur normal avec les , il suffit d'assimiler ces derniers aux vecteurs de base  tel que (trigonométrie élémentaire):

  (34.99)

et en  procédant de même pour tous les autres .

L'équilibre des forces nous donne:

  (34.100)

Après simplification:

  (34.101)

Suivant les autres axes:

  (34.102)

Soit en résumé:

  (34.103)

En utilisant la représentation matricielle, nous obtenons:

  (34.104)

Soit en notation indicielle les contraintes normales et tangentielles sont données par la relation traditionnelle suivante (où nous ne distinguons plus ce qui est tangentiel de ce qui est normal donc il y a une perte de clarté):

  (34.105) .

Nous voyons apparaître une grandeur mathématique  ayant 9 composantes, alors qu'un vecteur dans le même espace  en possède 3. Nous connaissons ce genre d'être mathématique que nous avons déjà étudié en algèbre dans le chapitre de Calcul Tensoriel. La grandeur  est appelée "tenseur des contraintes du second ordre". En outre, certaines composantes peuvent être égales (, si ) , ce qui le rendrait symétrique. Il ne possède alors plus que les 6 composantes distinctes, relativement aux nombres de composantes suffisantes pour décrire totalement un système à l'équilibre.

Pour étudier les déformations d'un milieu continu tel qu'un fluide, nous considérerons d'abord le cas de très faibles déformations. Les petits déplacements  d'un point seront représentés par u, v, w parallèles aux axes d'un référentiel OXYZ. Nous admettons que ces composantes sont des quantités très faibles variant d'une façon continue dans le volume du corps considéré.

Soit un segment linéaire OP situé dans un solide avant déformation. Dans un référentiel OXYZ, nous noterons  et   les coordonnées de O et P.

Pendant la déformation, la ligne OP devient O'P' tel que représenté ci-dessous:

Figure: 34.17 - Segment linéaire dans un solide avant et après déformation

Soient  les déplacements du point O parallèlement aux axes OX, OY, OZ et

 les déplacements du point P parallèlement aux mêmes axes.

Les coordonnées des points O' et P' sont alors:

 et   (34.106)

Avant déformation, soit L  la longueur OP :

  (34.107)

Après déformation, nous avons une longueur L' valant:

  (34.108)

Si  est l'allongement de l'élément OP pendant la déformation, nous avons:

  (34.109)

En effectuant les quelques transformations suivantes:

  (34.110)

En développant:

  (34.111)

Soit:

    (34.112)

En négligeant les termes de déplacement d'ordre supérieur et en tenant compte de la relation:

  (34.113)

il vient que disparaît avec  ainsi que les termes au carré, nous avons:

  (34.114)

Or, la géométrie analytique (trigonométrie élémentaire; rapport des côtés opposés et adjacents à l'hypoténuse) donne les relations suivantes:

  (34.115)

qui sont les cosinus directeurs de la droite L.

Nous pouvons alors écrire:

  (34.116)

La variation  étant un déplacement faible, nous avons recours à un développement en série de Taylor (cf. chapitres Suites Et Séries) dont nous négligeons les termes d'ordres supérieurs (linéarisation des équations):

  (34.117)

Nous avons également:

  (34.118)

La différence donne:

  (34.119)

Donc, nous pouvons maintenant écrire:

  (34.120)

Finalement:

  (34.121)

En groupant, nous avons:

  (34.122)

Cette expression permet en un point quelconque le calcul de la déformation  dans une direction ayant comme cosinus directeur  l, m, n  en fonction des déplacements  u, v, w en ce point!

Soit le cas où la ligne L coïncide avec l'axe OX, nous avons , l'équation précédente devient alors:

  (34.123)

Nous avons, si L coïncide avec l'axe OY  ou avec l'axe OZ :

  (34.124)

Les grandeurs  sont appelées "déformations normales" et n'ont pas d'unités.

Pour l'interprétation des termes , nous nous référerons à la figure suivante:

Figure: 34.18 - Situation permettant de faire émerger les tensions de cisaillement

Soient deux segments de droite OR et OQ situés dans le plan XOY. Avant déformation OR et OQ coïncidaient avec le référentiel orthonormé YOX. Après déformation, ils peuvent prendre la position O'R' et O'Q'. Les composantes du déplacement de O sont u, v .

- La composante du déplacement de R' est calculée comme suit:

 avec   (34.125)

car l'angle est faible .

En toute généralité comme , nous écrirons:

  (34.126)

- La composante du déplacement de Q' est elle:

  (34.127)

Comme avant déformation, l'angle QOR est de , après déformation, l'angle droit est réduit de . Cette réduction  est appelée "déformation de cisaillement" ou "déformation tangentielle" et est notée par .

Nous procéderons de la même façon pour les autres termes, d'où:

  (34.128)

Au vu de ce qui précède, il est d'usage de définir la "matrice d'opérateurs différentiels":

  (34.129)

Compte tenu du quadruplet de groupes d'équations démontrées précédemment dans cette section (voir les déformations des solides):

  (34.130)

Nous pouvons résumer:

  (34.131)

Au vu de ce qui précède, il est d'usage de définir la "matrice de transformation des contraintes en déformations":

  (34.132)

où il est possible d'inverser la matrice pour ainsi obtenir alors la matrice de transformation des déformations en contraintes.

Généralement, nous posons pour simplifier les notations (il faut cependant ne pas croire que la déformation en cisaillement devient une déformation normale! ce n'est qu'une convention d'écriture dont le physicien doit se rappeler!):

  (34.133)

De même, nous posons:

  (34.134)

Soit finalement:

  (34.135)

En tenant compte que:

  (34.136)

Nous obtenons les tensions de cisaillement comme suit:

  (34.137)

Considérons maintenant, pour exemple, un fluide circulant dans la direction de OY avec un gradient de vitesse dans la direction de x:

Figure: 34.19 - Situation permettant de faire émerger les contraintes normales

En se plaçant au niveau de y et au point 1 d'abscisse x, nous avons une vitesse  et au point 2 d'abscisse x+dx, une vitesse:

 (avec )   (34.138)

Dans la direction de x, il n'y a pas de composante de vitesse donc:

 (avec )   (34.139)

Nous supposons maintenant que les tensions de cisaillement sont proportionnelles à  à un facteur près tel que:

  (34.140)

avec pour rappel:

  (34.141)

Il est donc possible de considérer des déplacements par unité de temps en posant:

  (34.142)

En rapprochant cette dernière relation de:

  (34.143)

nous pouvons dire alors que G initialement valable dans un milieu élastique solide considéré par ses déplacements est l'analogue de dans le cas d'un fluide visqueux considéré par ses déplacements par unité de temps. Ainsi, nous voyons que les unités sont conservées.

En considérant également les déformations par unité de temps pour les contraintes normales (nous y reviendrons en détail un peu plus loin), nous avons alors le système d'équations:

  (34.144)

Ainsi, nous obtenons une écriture condensée:

  (34.145)

où  est le symbole de Kronecker:

=   (34.146)

Le tenseur  décrit ainsi en partie l'ensemble des contraintes d'un fluide visqueux dans lequel nous avons supposé dans le cadre de l'hypothèse d'un fluide newtonien qu'il y a des relations linéaires entre les tensions et les déformations normales.

Nous posons maintenant la somme des contraintes dynamiques sous une forme générale que nous allons justifier:

  (34.147)

où le terme se justifie par le fait que dans le cas statique, une pression dynamique constante p existe toujours en un point d'un fluide ce que l'on n'a pas dans le cas d'un solide. Pour justifier le signe négatif, nous observerons que dans l'expression de , les deux premiers termes du membre de droite correspondent, dans l'étude précédente, à des contraintes d'extension, alors que la pression p correspond à une compression du fluide.

Il nous reste  à présent, à déterminer le coefficient  .  Soit , nous avons alors . Il vient successivement et par addition:

  (34.148)

Cette expression doit répondre à un fluide qui est également dans une situation statique (au repos) telle que:

  (34.149)

Il vient alors que dans le cas statique:

  (34.150)

Puisque:

  (34.151)

Nous avons alors:

  (34.152)

L'expression générale des contraintes s'écrit alors:

  (34.153)

Présentement, nous allons introduire les opérateurs de l'analyse vectorielle afin de disposer d'une expression plus générale. De cette façon, nous pourrons adapter la formulation à n'importe quel système de coordonnées (cartésiennes, cylindriques, sphériques,...) ce qui facilitera la résolution de problèmes pratiques.

Nous avons vu que pour un solide, nous avions:

  (34.154)

Nous allons déterminer ces équations sous une forme indicielle en considérant toujours des déplacements par unité de temps (vitesses).

  (34.155)

tel que  et que

Pour  nous avons ainsi:

 ou   (34.156)

Pour  nous avons:

 ou   (34.157)

Nous pouvons dès lors écrire:

  (34.158)

En effectuant la somme des termes de:

  (34.159)

Or, les outils de l'analyse vectorielle nous permettent d'écrire:

  (34.160)

Pour le fluide, nous aurons ainsi:

  (34.161)

L'équation générale dynamique des contraintes s'écrira alors sous la forme suivante pour un fluide newtonien:

  (34.162)

Tenseurs des contraintes que certains auteurs notent (l'écriture est un peu dangereuse mais elle a une justification dans un cadre d'étude plus approfondi des fluides!):

  (34.163)

ou encore pour différencier vecteur et tenseur:

  (34.164)

Si les contraintes normales (fluide incompressible) sont négligeables le deuxième terme se simplifie et nous avons alors (relation que nous retrouverons dans le chapitre de Génie Marin Et Météo):

  (34.165)

Il est, à présent, utile de repasser sous une forme développée pour l'équation précédente, en se rappelant que (voir plus haut):

  (34.166)

Écrivons maintenant le système d'équations de Newton (sommes des contraintes dynamiques internes et externes à un élément de volume d'un fluide) qui est:

  (34.167)

où:

-  est la somme des forces externes par unité de volume

-  est la notation traditionnelle (malheureuse...) de l'accélération massique en

- est la densité du fluide

et qui peut s'écrire sous forme condensée:

  (34.168)

avec:

  (34.169)

Nous avons:

  (34.170)

En introduisant les expressions de  obtenues dans la relation ci-dessus, nous aboutissons aux équations:

  (34.171)

Ce sont les "équations de Navier-Stokes de la dynamique des fluides newtoniens". Il en existe deux formes condensées que nous allons de suite déterminer:

En reprenant la première équation de Navier-Stokes et en la développant, il vient:

  (34.172)

Comme:

  (34.173)

et que:

  (34.174)

Nous obtenons:

  (34.175)

En simplifiant, il vient finalement:

  (34.176)

En opérant de la même manière pour les deux autres composantes, nous pouvons réduire le système d'équations de Navier-Stokes à une seule équation vectorielle:

  (34.177)

Comme (cf. chapitre de Calcul Vectoriel) le laplacien vectoriel est donné par:

  (34.178)

Nous avons:

  (34.179)

Soit au final:

  (34.180)

Remarque: Nous trouvons également parfois dans la littérature, une équation contenant une seconde viscosité , alors que  ne se manifeste rigoureusement que lors du cisaillement pur selon nos hypothèses,   apparaît lors d'une compression omnidirectionnelle s'accompagnant d'une variation de densité.

L'équation précédente s'écrit alors:

  (34.181)

C'est "l'équation de Navier-Stokes" ou aussi appelée "équation de mouvement pour un fluide newtonien".

FLUIDE INCOMPRESSIBLE

Dans un fluide incompressible, nous avons par définition . L'équation de conservation qui est (cf. chapitre de Thermodynamique):

  (34.182)

s'écrit alors:

  (34.183)

soit la divergence du champ de vitesse est nulle:

  (34.184)

L'équation de Navier-Stokes sous la forme:

  (34.185)

s'écrit alors:

  (34.186)

ou autrement:

  (34.187)

Si de plus la viscosité  est négligeable, nous avons donc pour un fluide parfait:

  (34.188)

Cette équation est appelée "équation d'Euler de 1ère forme" ou encore "équation locale du bilan de conservation de la quantité de mouvement". Nous réutiliserons cette relation dans le cadre de notre étude des ondes de gravité (vagues) dans le chapitre de Génie Météo Et Marin.

Il existe une deuxième forme de l'équation d'Euler dans le cadre d'un fluide incompressible et à viscosité négligeable que nous allons de suite déterminer (souvent utilisée dans l'industrie):

Si , nous pouvons écrire:

  (34.189)

Ce qui peut aussi s'écrire:

  (34.190)

Ce qui s'écrit encore:

  (34.191)

Le premier facteur peut être considéré comme le produit scalaire suivant:

  (34.192)

Soit:

  (34.193)

La "dérivée particulaire" peut alors prendre la forme condensée suivante:

  (34.194)

où l'expression entre parenthèses est le "terme d'advection". L'advection est le transport d'une quantité scalaire ou vectorielle conservée, par un champ vectoriel. Un exemple est le transport de matière polluante par le flux d'une rivière. En météorologie et en océanographie, l'advection se réfère surtout au transport horizontal de certaines propriétés par les fluides considérés, dont le transport par le vent ou les courants : advection de vapeur d'eau, de chaleur, de salinité, etc.

L'équation d'Euler de 1^ère forme:

  (34.197)

devient compte tenu de la dérivée particulaire:

  (34.198)

ou encore (forme courante dans la littérature):

  (34.199)

Nous avons vu dans le chapitre de Calcul Vectoriel que:

  (34.200)

Si nous posons , nous avons:

  (34.201)

Soit:

  (34.202)

Finalement, nous obtenons une nouvelle équation appelée "équation d'Euler de 2ème forme" et qui s'écrit:

  (34.203)

Bien que les deux équations d'Euler soient très importantes, il en existe une forme variée très utile en météorologie que nous allons de suite déterminer.

Nous nous basons toujours sur l'écoulement d'un fluide incompressible et non visqueux, mais  dont les forces de volume dérivent cette fois-ci d'un potentiel  (U étant un potentiel).

Dans ce cas, nous recourons à l'équation d'Euler sous sa 1^ère forme:

  (34.204)

Puisque les forces volumiques dérivent d'un potentiel U, nous avons:

  (34.205)

Nous rappelons la relation:

  (34.206)

Soit  un vecteur , il vient:

  (34.207)

donc:

  (34.208)

donc nous pouvons aussi écrire:

  (34.209)

En reprenant la relation:

  (34.210)

l'équation:

  (34.211)

devient alors:

  (34.212)

et en utilisant:

  (34.213)

cette dernière devient:

  (34.214)

et puisque:

  (34.215)

nous pouvons finalement écrire:

  (34.216)

Généralisons cette dernière relation en faisant apparaître d'éventuelles rotations. Pour cela, nous savons que donc:

  (34.217)

En écrivant le produit vectoriel  sous forme développée, nous avons:

  (34.218)

Ce qui donne:

  (34.219)

Supposons que  soit un vecteur vitesse angulaire constant, nous avons alors:

  (34.220)

Définition: Nous disons qu'un "écoulement est tourbillonnaire" si le rotationnel du champ de vitesse est non nul:

  (34.221)

partout ou en certains points. Nous définissons aussi de la relation antéprécédente la "vorticité" par:

  (34.222)

Exemple d'écoulement partiellement tourbillonnaire (en certains points):

Figure: 34.20 - Exemple d'un écoulement tourbillonnaire

L'équation:

  (34.223)

s'écrit alors:

  (34.224)

Nous retrouvons dans cette équation, utilisée en météorologie, l'accélération de Coriolis que nous avions déterminée dans le chapitre de Mécanique Classique.

Si l'écoulement s'effectue à vitesse constante  et n'est pas rotationnel (non turbulent)  , alors l'équation précédente se réduit à:

  (34.225)

En dynamique classique du point matériel rigide, nous avons montré que dans le cas d'un potentiel gravitationnel Terrestre:

  (34.226)

z étant l'altitude d'un point du fluide par rapport à un niveau de référence . Si nous prenons  pour le niveau du sol, l'avant-dernière relation devient donc dans le cas d'un écoulement dit alors "écoulement potentiel":

  (34.227)

Le terme entre crochets pour satisfaire cette relation doit être tel que:

  (34.228)

Nous retrouvons donc bien le théorème de Bernoulli, ce qui conforte notre modèle des fluides newtoniens selon le modèle de Navier-Stokes.

Si inversement l'écoulement est tourbillonaire, donc tel que:

  (34.229)

Or, comme nous l'avons démontré dans le chapitre de Calcul Vectoriel, si le rotationnel d'une variable vectorielle est nul, la variable peut être exprimée comme le gradient d'un potentiel scalaire! Dès lors, dans le cas tourbillonaire, le champ de vitesse dérive alors d'un potentiel de vitesse:

  (34.230)

Et si en plus le le fluide est incompressible, comme nous l'avons vu plus haut:

  (34.231)

Alors en combinant les deux dernières relations il vient (divergence du gradient):

  (34.232)

Soit explicitement:

  (34.233)

Le potentiel des vitesses dans le cas d'un liquide incompressible et non-tourbillonaire vérifie donc l'équation de Laplace!

FLUIDE COMPRESSIBLE

Dans ce cas  est une fonction de la pression p (cas des "fluides barotropes"). Nous considérons également que la viscosité est négligeable. Il vient alors:

  (34.234)

L'équation:

  (34.235)

s'écrit alors:

  (34.236)

FLUIDE STATIQUE

Dans le cas statique  et    l'équation:

  (34.237)

devient simplement:

  (34.238)

qui est "l'équation de la statique des fluides" ou la "loi fondamentale de l'hydrostatique". Sous forme discète et plus classique (réarrangée), nous retrouvons le relation des manuels scolaires:

  (34.239)

ou encore en prenant la hauteur initiale comme étant nulle:

  (34.240)

NOMBRE DE REYNOLDS

Considérons d'abord, pour simplifier, le cas incompressible.

L'équation de continuité, ou de conservation de la masse, (cf. chapitre de Thermodynamique):

  (34.241)

s'écrit alors dans ce cas particulier:

  (34.242)

Nous choisissons maintenant plusieurs grandeurs de références sans dimensions notées par un indice r telles que:

 et      (34.243)

De par ces définitions, nous avons par exemple:

  (34.244)

donc l'équation des déformations par unité de temps devient:

  (34.245)

Mais nous avons également:

  (34.246)

Restreignons-nous à l'étude d'une composante seulement:

  (34.247)

En multipliant cette dernière relation par la densité et par définition de la vitesse:

  (34.248)

Reprenons maintenant une des formulations possible de l'équation de Navier-Stokes démontrée plus haut:

  (34.249)

En n'oubliant pas que pour un fluide incompressible nous avons:

  (34.250)

l'équation de Navier-Stokes précédente, se réduit à:

  (34.251)

Or, pour un fluide nous avions supposé plus haut que les tensions de cisaillement étaient données par:

  (34.252)

Les termes où apparaissent les coefficients de viscosité peuvent être réécrits tels que:

  (34.253)

Ainsi par correspondance:

  (34.254)

que nous pouvons écrire sous forme encore plus condensée en utilisant un peu abusivement la notation tensorielle:

  (34.255)

En introduisant les variables adimensionnelles:

  (34.256)

Maintenant, multiplions cette dernière relation par  et divisons-la par des deux côtés de l'égalité tel qu'elle devienne:

  (34.257)

Au niveau dimensionnel, remarquons que nous avons:

  (34.258)

Finalement:

  (34.259)

Cette équation différentielle exprimée en variables relatives et sans dimensions est appelée "équation de Navier-Stokes-Reynolds adimensionnelle"

Le terme , appelé "nombre de Reynolds", représente au niveau symbolique le rapport des forces d'inerties sur les forces visqueuses:

  (34.260)

où  est la "viscosité cinématique relative". La viscosité dynamique est donc un terme inversement proportionnel à la valeur du nombre de Reynolds.

Nous retrouvons également souvent cette dernière relation sous la forme suivante (identification terme à terme avec la première égalité de l'expression précédente où 2R est le diamètre de la section circulaire du tube qui transporte le fluide):

  (34.261)

Si en lieu et place de la vitesse c'est le débit massique qui est mesuré à travers une section circulaire, nous avons alors en utilisant la relation suivante entre débit massique et vitesse de fluide dans un tube cylindrique:

  (34.262)

Une autre écriture pour la relation antéprécédente que nous retrouvons souvent dans la pratique industrielle:

  (34.263)

Dans la pratique nous calculons régulièrement le temps qu'il faudrait pour remplir un réservoir de volume donné avec un fluide ayant un débit massique, une densité, une viscosité et un Nombre de Reynolds connus dans un tuyau clindrique dont les rayon est lui aussi connu. Dès lors, il vient:

  (34.264)

APPROXIMATION DE BOUSSINESQ

Soit la relation déjà démontrée précédemment:

  (34.265)

En y remettant le terme contenant la viscosité:

  (34.266)

sans oublier qu'au niveau des notations (nous savons… c'est un peu embêtant):

  (34.267)

Si le potentiel est de type gravitationnel, il va de soi que:

  (34.268)

Donc:

  (34.269)

Si l'on peut considérer le contexte de l'expérience telle que la densité volumique est inférieure ou égale à celle de l'eau et que les vitesses sont petites, alors nous pouvons éliminer les termes de second degré, tel que la relation précédente s'écrive:

  (34.270)

Nous nous plaçons dans le cadre d'un fluide faiblement turbulent, dans lequel la pression et la densité s'écrivent:

  (34.271)

où  représentent le terme d'accroissement turbulent par rapport aux valeurs statiques du fluide.

Nous négligeons également les frottements sur les bords et donc la viscosité en supposant que l'effet des turbulences devient vite prépondérant sur la valeur du frottement.

Donc, nous avons le système d'équations:

  (34.272)

qui peut s'écrire:

  (34.273)

et encore:

  (34.274)

ce qui s'écrit aussi:

  (34.275)

Mais dans le cas statique:

  (34.276)

Il nous reste donc:

  (34.277)

En divisant le tout par :

  (34.278)

mais encore une fois:

  (34.279)

L'approximation de Boussinesq consistant à supposer que le fluide est incompressible et que le système est à température constante et peu turbulent, nous avons:

  (34.280)

Ce qui nous donne:

  (34.281)

Cette équation s'appelle "équation de Boussinesq" et va nous permettre d'introduire la théorie du chaos dans le domaine de la météorologie et des fluides dans le cas particulier des cellules de convection.

LOI DE STOKES

La complexité de l'hydrodynamique est un terrain tout désigné pour l'application de l'analyse dimensionnelle dont nous avons parlé au tout début de notre étude de la mécanique analytique. L'exemple analysé ici montre clairement les possibilités, mais aussi les limites de la méthode.

Nous envisageons un solide de forme quelconque plongé dans un fluide incompressible animé d'une vitesse uniforme à grande distance (le problème est équivalent à celui d'un solide qui se déplace à vitesse constante dans un fluide au repos). Nous cherchons à exprimer la force F qu'exerce le fluide sur l'obstacle, supposé immobile (et notamment dépourvu de tout mouvement de rotation).

La solution analytique est trop complexe pour perdre son temps à résoudre ce genre de problème pratique. Il convient de recourir à l'analyse dimensionnelle.

Les paramètres pertinents sont dans notre étude:

- L la dimension linéaire de l'obstacle

- v la vitesse du fluide à grande distance

-  la masse du fluide

-  le coefficient de viscosité du fluide

Comme il se doit, tous ces paramètres sont des constantes, bien que la vitesse varie en direction et en norme au voisinage de l'obstacle: à grande distance, elle est uniforme et sa valeur v est bien un paramètre pertinent.

Nous pourrions nous demander si la pression ne devrait pas compter au nombre de ces paramètres. Ce n'est pas le cas. La pression est conditionnée par la valeur de la vitesse et par celles des paramètres constants comme nous l'avons voyons dans le théorème de Bernoulli. Inutile donc de rajouter un terme redondant.

Sans chercher l'unique combinaison sans dimension des quatre premières, nous appliquons la démarche systématique. Nous voulons déterminer A, B, C, D, tels que:

  (34.282)

Comme:

  (34.283)

Il vient:

  (34.284)

Le système de dimensionnalité s'écrit:

  (34.285)

Ainsi:

  (34.286)

Dès lors:

  (34.287)

et curieusement nous retrouvons ici ce que nous avions vu dans notre développement de l'approximation de Boussinesq:

  (34.288)

Donc la force exercée par le fluide s'écrit:

  (34.289)

Dans la littérature, nous trouvons la notation:

  (34.290)

où C dépend de . Nous retrouvons également cette relation sous la forme condensée:

  (34.291)

où n'apparaît le coefficient de trainée qui est déterminé dans les souffleries ou expérimentalement en se basant sur le fait qu'un objet en chute libre dans un liquide ou un gaz parfait suivra l'équation différentielle:

  (34.292)

Équation différentielle que nous pouvons résoudre astucieusement en écrivant:

  (34.293)

Il vient alors après réarrangement des termes:

  (34.294)

Soit après intégration:

  (34.295)

Il vient alors une relation qui permet de déterminer expérimentalement le coefficient de trainée pour un objet en chute libre sans trop de difficultés:

  (34.296)

Les limites de la méthode analytique dimensionnelle (et même analytique tout court…) apparaît lorsque l'on confronte ce modèle à l'expérience (évidemment nous pourrions faire des modèles numériques de l'équation de Navier-Stokes-Reynolds pour l'ordinateur et ainsi l'honneur serait sauf):

Figure: 34.21 - Illustration du paramètre C pour un cylindre dans différents régimes

Ce graphique correspond à l'écoulement autour d'un cylindre; la vitesse  étant perpendiculaire à l'axe du cylindre. Les régimes sont signalés en chiffres romains: stationnaire (I), périodique laminaire (II), turbulent avec superposition d'état périodique (III), turbulent (IV).

La courbe a deux caractéristiques remarquables:

1. Elle a été obtenue en modifiant de manière indépendante les valeurs des quatre paramètres. Nous constatons que C ne dépend que du seul nombre sans dimension : c'est un succès de l'analyse dimensionnelle.

2. Il est vain d'espérer trouver une fonction analytique simple qui reproduise la courbe expérimentale. Il faut donc aller voir de plus près les divers régimes correspondants à cette courbe complexe.

La figure ci-dessous schématise l'écoulement d'un fluide visqueux autour d'un cylindre pour différentes valeurs du nombre de Reynolds:

Figure: 34.22 - Écoulements autour d'un cylindre en fonction de différentes valeur du nombre de Reynolds

Le régime correspondant à la figure (a) est dit "régime stationnaire". Nous pouvons parler d'un déplacement "quasi-statique" de la part du fluide où en chaque point l'accélération est négligeable. Nous devons donc nous attendre à ce que l'inertie du fluide n'intervienne pas dans l'expression de la force. Pour cela, il faut et il suffit que:

  (34.297)

où C est indépendant de .

Nous avons donc:

  (34.298)

Le paramètre C' sans dimensions ne peut dépendre que de la géométrie de l'obstacle. Dans le cas où l'obstacle est sphérique (cas très important en physique avec L=R), C' a été déterminé expérimentalement comme valant  tel que:

  (34.299)

connue sous le nom de "loi de Stokes" ou "formule de Stokes". Attention.... cette loi ne s'applique bien que pour les petites vitesses et des petites sphères.

Dans le régime décrit par (b), deux tourbillons s'installent symétriquement derrière le cylindre. Quand  augmente au-delà de 40, nous distinguons l'allée de "tourbillons de von Kármán".

PRESSION HYDROSTATIQUE

Nous avons précédemment démontré sans mal que:

  (34.300)

Si la vitesse du fluide est nulle:

  (34.301)

Ce qui donne sous forme différentielle:

  (34.302)

Si nous mesurons la pression du liquide à partir de sa face supérieure :

  (34.303)

Si nous prenons  comme référence, nous pouvons poser que:

  (34.304)

d'où:

  (34.305)

Si nous nous trouvons dans le cas d'un récipient rempli d'un fluide en contact avec l'atmosphère, pour calculer la pression dans ce fluide à une hauteur h donnée, il faudrait prendre en considération la pression atmosphérique qui "s'appuie" également sur le fluide. Ainsi, la "pression hydrostatique" est donnée par:

  (34.306)

Conséquence: Dans un liquide au repos, homogène, les équipotentielles gravifiques sont confondues avec les surfaces isobares. Sans quoi, il y aurait mouvement transversal.

POUSSÉE D'ARCHIMÈDE

La poussée d'Archimède, phénomène mondialement connu..., est souvent rebelle à l'intuition première. Au fait, nous avons trop tendance dans les écoles à poser la poussée d'Archimède comme un "principe" et ce à tort puisqu'une simple analyse mathématique suffit à la démontrer .

Si nous isolons une portion  arbitraire d'un fluide en équilibre statique, les conditions de cet équilibre s'écrivent nécessairement (sinon quoi le volume se dissocie et n'est plus en équilibre statique):

  (34.307)

 désigne le poids ( en première approximation…) de  alors que le terme  décrit la résultante des forces de pression exercée sur la surface de .

Chaque élément de surface dS subit donc une force:

  (34.308)

où p est la pression qui s'exerce localement sur dS. Quant à , il s'agit d'un vecteur unité dirigé normalement (à la perpendiculaire) à dS et vers l'intérieur de . La résultante de toutes ces forces se note historiquement de la façon suivante:

  (34.309)

qui exprime donc, comme vous le devinez, la fameuse "poussée d'Archimède" que le reste du fluide exerce sur l'élément. L'intégrale porte sur toute la surface (cette surface est fermée, d'où l'intégrale curviligne correspondante) de l'élément .

La condition d'équilibre impose donc que:

  (34.310)

Nous comprenons aisément que  soit dirigé vers le haut: sous l'effet du champ gravitationnel et donc p augmente avec la profondeur.

Si nous remplaçons le fluide contenu dans le volume par un objet fluide ou solide quelconque mais qui occupe le même volume, la poussée d'Archimède n'est pas modifiée. À cause de la relation  nous avons coutume de dire qu'elle est équivalente au poids du fluide déplacé.

Dans le cas où la direction et l'intensité dans le temps de  sont uniformes et constantes  nous pouvons écrire:

  (34.311)

et nous retrouvons la relation de la "loi d'Archimède" bien connue de tous les écoliers:

  (34.312)

Il existe une autre possibilité pour arriver à cette démonstration qui demande moins d'outils mathématiques et qui est donc plus abordable:

Considérons un cylindre de volume V plongé dans un liquide à la verticale. Les composantes horizontales des forces de pression s'annulent, mais la composante verticale au sommet du cylindre  (proche de la surface) est inférieure en intensité (sauf cause extérieure) à celle se trouvant à sa base . Nous pouvons donc écrire:

  (34.313)

C'est un peu plus simple et ça tient en une ligne sans intégrales…

Il convient de se rappeler que la poussée d'Archimède est une force qui s'applique à des fluides et donc aussi à des gaz. C'est ainsi grâce à la poussée d'Archimède qu'une montgolfière ou un dirigeable peuvent s'élever dans les airs (dans les deux cas, un gaz de masse volumique plus faible que l'air est utilisé, que ce soit de l'air chauffé ou de l'hélium).

Il est aussi amusant, après démonstration de la loi des gaz parfaits (voir plus loin), de déterminer la pression que devrait avoir notre atmosphère pour avoir la même densité que l'eau et qu'un humain puisse ensuite flotter dans l'air...

VITESSE DU SON DANS UN LIQUIDE

Intéressons-nous un petit moment au calcul de la vitesse du son dans un liquide. Nous avons démontré dans le cas de notre étude des ondes sonores longitudinales du chapitre de Musique Mathématique que:

  (34.314)

où pour rappel, 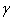est le "coefficient de Laplace", appelé aussi "coefficient adiabatique" défini par:

  (33.315)

et nous avions démontré que la vitesse de l'onde sonore était donnée par:

  (34.316)

En combinant il vient:

  (34.317)

La fraction:

c'est-à-dire le rapport entre une variation de pression et la variation relative de volume qu'elle entraîne reçoit le nom de "module d'élasticité volumique". Remarquez qu'il faut le signe - pour que B soit positif: quand la pression augmente, le volume diminue.

Nous avons alors par exemple pour l'eau:

  (34.318)

La valeur mesurée étant de . Il peut paraître surprenant que la vitesse du son dans un liquide, qui est beaucoup plus difficile à comprimer qu'un gaz soit seulement 5 fois plus grande que dans un gaz. La raison est que la densité d'un liquide est environ mille fois plus élevée que celle d'un gaz. L'une dans l'autre, les deux propriétés se compensent partiellement.

9   0

Notée par 18 visiteur(s) 12345 PageRater 0.5.0 Commentaires: [0]