|

DYNAMIQUE DES POPULATIONS | THÉORIE
DES JEUX ET DE LA DÉCISION | ÉCONOMIE
TECHNIQUES DE GESTION | MUSIQUE MATHÉMATIQUE
Dernière mise à jour de ce chapitre:
2017-01-31 10:13:41 | {oUUID 1.806}
Version: 3.3 Révision 41 | Avancement:
~70%
 vues
depuis
le 2012-01-01:
5'390 vues
depuis
le 2012-01-01:
5'390
 LISTE DES SUJETS TRAITÉS SUR CETTE PAGE
LISTE DES SUJETS TRAITÉS SUR CETTE PAGE
ANALYSE DES SÉRIES TEMPORELLES (A.S.T)
Contrairement à l'économétrie traditionnelle,
le but de "l'analyse des séries temporelles" (A.S.T.)
n'est pas de relier des variables entre elles, mais de s'intéresser à la
dynamique d'une variable dans le temps pour découvrir certaines
régularités afin de pouvoir
extrapoler ou d'établir des prévisions sous réserve
de l'hypothèse
qu'on puisse relier une observation à celles qui l'ont précédée.
Avec une analyse fine, il est même possible d'établir des
prévisions "robustes" vis-à-vis
de ruptures brusques et de changements non-anticipables.
Remarque: Ce domaine est un souvent
appelé "Business
Intelligence" dans
les entreprises (il s'agit d'une sous-famille en réalité).
Une variable analysée
sous forme d'A.S.T. sera elle appelée
un "Indice de Performance Clé" (IPC) et un ensemble
d'IPC un "tableau de bord".
Définition: Une "série
temporelle à temps discret" ou "série
chronologique à temps discret" (plus rigoureusement on devrait parler de "suite"!)
est une suite d'observations 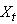 d'une
variable y à différentes dates t. Habituellement
l'espace de base de t est dénombrable, de sorte que d'une
variable y à différentes dates t. Habituellement
l'espace de base de t est dénombrable, de sorte que 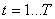 .
Le tout étant noté: .
Le tout étant noté:
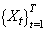 (66.1)
(66.1)
et parfois le Y majuscule est noté par un X (cela
importe peu...).
Attention! On différencie de façon importante les
modèles qui prédisent
des valeurs réelles de ceux qui doivent prédire des
valeurs purement entières (données de comptage). À ce
jour, le contenu de ce site Internet ne traite que des modèles
particulièrement
adaptés aux variables
continues.
Une série temporelle est donc toute suite d'observations correspondant à la
même variable: il peut s'agit de données macroéconomiques (le PIB
d'un pays, l'inflation, les exportations), microéconomiques (les
ventes d'une entreprise donnée, son nombre d'employés, le revenu
d'un individu, ...), financières (le CAC40, le prix d'une option
d'achat ou de ventre, le cours d'une action), météorologiques (la
pluviosité, le nombre de jours de soleil par an...), politiques (le
nombre de votants, de voix reçues par un candidat...), démographiques
(la taille moyenne des habitants, leur âge...).
En pratique, tout ce qui est chiffrable et varie en fonction
du temps peut être analysé relativement pertinemment sous
forme de AST tant que la personne qui manipule le modèle
sait ce qu'elle fait (ce qui est rare dès qu'on sort du
domaine public et étatique...).
Ainsi en finance on utilise ces modèles pour modéliser les rendements
mais aussi la volatilité (écart-type) et la VaR.
Bref, il n'y pas vraiment de limites à l'application.

Figure: 66.1 - Quelques séries temporelles
La dimension temporelle est ici importante car il s'agit de l'analyse
d'une chronique historique: des variations d'une même variable
au cours du temps, afin de pouvoir en comprendre la dynamique.
On représente en général les séries
temporelles sur des graphiques de valeurs (ordonnées) en
fonction du temps (abscisses). Une telle observation constitue
un outil essentiel qui permet au modélisateur
ayant un peu d'expérience de tout de suite se rendre compte
des propriétés dynamiques principales, afin de savoir
quel test statistique pratiquer. La figure précédente
montre différentes séries temporelles à titre
d'exemples.
Une série temporelle se décompose principalement en trois éléments
de base:
1. La "tendance séculaire à long
terme" ou "trend".
Elle correspond
à un mouvement conjoncturel non saisonnier qui traduit l'évolution
à long terme de la variable mesurée.
2. Les "variations saisonnières" sont
des fluctuations périodiques
qui se produisent régulièrement (périodiquement:
jours, mois, trimestres ou années).
3. Les "aléas" ou "variations
résiduelles/accidentelles" sont
des fluctuations de type aléatoires, en général de faible amplitude.
Définitions:
D1. Les séries qui oscillent autour de leur moyenne sont
appelées "séries
stationnaires" (nous verrons une définition
rigoureuse un peu plus loin).
D2. Les séries qui semblent croître ou baisser sur
l'ensemble de l'échantillon observé sont appelées
des "séries tendancielles" et
leurs moyennes ne sont pas constantes.
D3. Les séries qui ne sont ni stationnaires ni tendancielles
haussière
ou baissière à long terme sont appelées "séries
non-stationnaires" ou "séries
aléatoires" ou encore
"séries stochastiques".
T out processus dont l'évolution temporelle peut être
analysée
en termes de probabilité est donc dit "processus
stochastique".
D4. Les séries qui présentent une périodicité (fluctuation)
régulière
sont appelées "séries
saisonnières". Régulièrement,
les séries stationnaires
sont des séries tendancielles avec une composante
périodique.
D5. Les séries qui semblent saisonnières ou semblent avoir une
composante saisonnière mais dont la périodicité est variable, sont
appelée "séries cycliques".
Soit 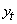 une
valeur de la série, une
valeur de la série, 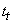 sa
composante tendancielle, sa
composante tendancielle, 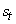 sa
composante saisonnière et sa
composante saisonnière et 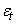 sa
partie aléatoire, nous définissons: sa
partie aléatoire, nous définissons:
- Un modèle additif par une expression du type:
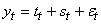 (66.2)
(66.2)
- Un modèle multiplicatif simple:
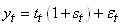 (66.3)
(66.3)
où nous avons donc que la composante saisionnière
est liée à la composante tendancielle (à l'opposé du modèle additif
où la composante saisonnière est la même d'un multiple de périodes
à l'autre).
- Un modèle multiplicatif complet:
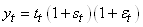 (66.4)
(66.4)
- Un modèle mixte:
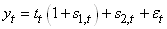 (66.5)
(66.5)
Les caractéristiques de ces graphiques sont toutes modélisables
et analysables dans le cadre de l'analyse des séries temporelles.
Il existe pour cela des outils plus ou moins complexes dont certains
ne peuvent être mis en doute et dont d'autres sont des modèles
heuristiques qu'il faut savoir manipuler et utiliser avec précaution.
Dans le texte qui va suivre, nous allons nous intéresser qu'aux
modèles élémentaires accessibles sans une artillerie mathématique
lourde.
L'humilité dans le métier de prévisionniste est cependant de mise
pour accepter l'erreur de manière récurrente, tout en cherchant à améliorer
la qualité de ses prévisions (ventes, volatilité des marchés,
corrélation d'actifs, etc.) et l'identification des composantes non aléatoires
des phénomènes. Il convient de se rappeler des 4 critères suivants:
1. Les prévisions sont très généralement inexactes. Il faut donc
un écosystème robuste pour réagir rapidement à l'imprévu (savoir
que l'on ne peut pas prévoir, ne signifie pas que l'on ne peut
pas tirer profit de l'imprévisibilité) ce ce d'autant plus que
certains multinations (dont je vais taire le nom... demandent des
projections sur 20 mois!!!).
2. Une bonne prévision est plus qu'une valeur numérique. Puisque
les prévisions sont généralement inexactes, une bonne prévision
doit également inclure une mesure de l'erreur anticipée pour la
prévision
3. Les prévisions agrégées sont plus précises. De manière générale,
nous remarquons que l'erreur faite pour la prévision de ventes
d'une ligne de produits est généralement moindre que l'erreur faite
dans la prévision de ventes d'un seul élément.
4.
Les prévisions à long terme sont moins précises. Il n'y a pas grand-chose à en
dire car c'est intuitif...
5. Les prévisions peuvent être sensibles aux conditions initiales
(pensez aux modèles chaotiques de la météorologie ou de la dynamique
des populations...)
Remarque: Les exemples de cas où de
grands dirigeants de multinationales ont, faute de connaissances
statistiques ou mal conseillés par
des gestionnaires non statisticiens/non économistes, fait des prévisions
de bénéfices ou ventes sur plus de 10 à 20 ans (ce qui est une
aberration!!) dans les médias sont légion! Évidemment les chiffres
donnés et la stratégie de développement associée ont conduit certaines
de ces multinationales à la quasi-catastrophe.
Signalons que les techniques prévisionnelles quantitatives utilisent également
et principalement les outils suivants (il est bien évidemment possible
de les combiner) pour lesquels nous avons déjà donné des exemples
dans les chapitres respectifs:
- Marche aléatoire simple (cf. chapitre
d'Économie)
- Régression linéaire simple (cf.
chapitre de Méthodes Numériques)
- Régression linéaire
multiple (cf. chapitre
de Méthodes Numériques)
- Régression logistique (cf.
chapitre de Méthodes Numériques)
- Interpolation polynomiale
(cf. chapitre
de Méthodes Numériques)
- Linéarisation logarithmique et
exponentielle (cf.
chapitre de de Méthodes Numériques)
- Modélisation
par mouvement brownien (cf.
chapitre d'Économie)
- Moyenne Mobile (cf. chapitre de Statistiques)
-
Analyse de corrélations (cf. chapitre
de Statistiques)
- Cartes de contrôle (cf.
chapitre de Génie
Industriel)
- Réseaux de neurones (cf.
chapitre de Méthodes Numériques)
et ils peuvent être regroupés en deux familles principales:
1. Les modèles causes-effets basés sur plusieurs variables explicatives
2. Les modèles en série chronologique dont la seule variable
explicative est le temps
et c'est toujours délicat pour un prévisionniste de choisir laquelle
est la mieux adaptée à son cadre de travail et au niveau de compréhension
de ses supérieurs. La partie intéressante du métier est qu'une
fois le ou les modèles choisis (encore faut-il choisir parmi la
centaine de modèles empiriques publiés...), nous pouvons les confronter
aux données statistiques passées de l'entreprise et voir si les
prévisions
sont en accord avec ce qui c'était réellement passé.
Remarque: Il est préférable d'utiliser des modèles basés sur
les statistiques que des modèles déterministes qui sont de piètre
qualité (comme la moyenne mobile simple ou double ainsi que les
lissages exponentiels et régressions linéaires simples ou multiples).
TYPES D'ERREURS
Avant de construire des modèles de prévision il
faut pouvoir estimer la qualité de celle-ci (à des fins
de comparaison aussi entre modèles) et pour cela il est
d'usage d'utiliser plusieurs indicateurs empiriques qui sont:
- "L'erreur prévisionnelle":
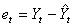 (66.6)
(66.6)
qui est donc la différence entre le réel et la modélisation.
- "L'écart-moyen" ou "biais
de prévision" ("Mean Error" en anglais):
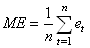 (66.7)
(66.7)
qui va seulement nous dire s'il y une erreur systématique positive
ou négative entre la prévision et le réel (car si la valeur de ME est
non nulle, le modèle est biaisé). Mais comme cette valeur est souvent
très petite (les valeurs négatives équilibrant les positives dans
certains modèles) nous lui préférons la mesure d'erreur suivante:
- "L'écart moyen absolu" ("Mean
Absolute Deviation" ou "Mean Absolute Error" ou
encore "Mean Forecast Error" en anglais):
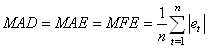 (66.8)
(66.8)
qui est la moyenne des erreurs absolues faites par le modèle
de prévision sur toute la durée de celle-ci, sans égard au fait
que l'erreur soit une surestimation ou une sous-estimation.
- Le "carré moyen des résidus" ("Mean
Square Deviation" ou "Mean Square Errors" en anglais):
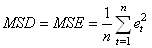 (66.9)
(66.9)
qui permet de pénaliser les grandes erreurs plus que les petites
puisque chaque erreur est multipliée par elle-même, donnant ainsi
un poids plus grand aux grandes erreurs qu'aux petites erreurs.
Le problème avec les indicateurs précédents est que l'amplitude
de l'erreur dépend des amplitudes des valeurs analysées. Pour éviter
cet inconvénient, il est plus intéressant de travailler avec un
pourcentage (valeur relative). Ainsi, nous définissons "l'erreur
relative" indiquée en pourcents ("Percentage Error" en
anglais) par:
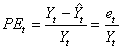 (66.10)
(66.10)
qui est donc la différence en pourcents entre le réel et la modélisation
par rapport au réel. Il s'ensuit alors "l'erreur
relative moyenne" ou "biais
relatif de prévision" ("Mean Percentage Error" en
anglais) toujours indiquée en
pourcents:
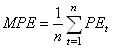 (66.11)
(66.11)
Pour les mêmes raisons que l'indicateur ME nous lui préférons
la mesure d'erreur suivante.
- "L'écart relatif moyen absolu" ("Mean
Absolute Percentage Error" en anglais) toujours indiqué en
pourcents:
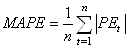 (66.12)
(66.12)
Le seul problème avec les indicateurs relatifs c'est lorsque
la série temporelle analysée contient des zéros...
- Les "moments temporels" sont
les deux paramètres de position et de dispersions élémentaires
en statistiques que sont la moyenne et l'écart-type masi pris simplement
sur une certaine période temporelle (très utilisé en finance!).
Ainsi, la moyenne d'une variable mesurée sur une fenêtre [t-p,t]
sera donnée triviallement par:
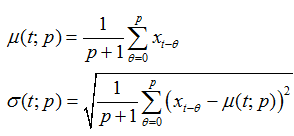 (66.13)
(66.13)
- Le "hit score" (très utilisé
en finance des marchés) dont l'idée est très simple. Il s'agit
simplement du ratio du nombre de bonne prévisions périodiques (le
concept de "bonne" étant empirique car il existe des dizaines de
choix) sur le nombre total de périodes passées.
Enfin, pour clore cette partie concernant les indicateurs, signalons
que dans le domaine du prévisionnel il faut aussi vérifier
sur le long terme si un modèle théorique est viable
ou non pour le remplacer par un autre. Les techniques de base pour
cela consistent à faire usage des cartes de
contrôles
autocorrélées (cf. chapitre
de Génie Industriel)
où les mesures seront simplement les écarts (sans
en prendre la valeur absolue!) entre les valeurs projetées
et ce qui a réellement eu lieu.
DÉCOMPOSITION
Certains modèles utilisant les séries chronologiques sont des
outils de prévision adéquats pour autant que la variation ait montré un
patron stable dans le temps et que les conditions dans lesquelles
le patron est
apparu s'appliquent toujours.
Parfois, un patron n'est pas apparent lors de l'analyse
des données brute; celles-ci peuvent toutefois être décomposées
de manière à révéler des patrons qui facilitent la projection des
données dans le futur (nous verrons la décomposition par transformée
de Fourier plus loin). Voici les quatre composantes généralement
reconnues (et déjà mentionnées plus haut) pour les séries chronologiques
hors analyse spectrale: tendance (linéaire, exponentielle,
sigmoïde, etc.), saisonnalité, cyclicité, aléatoire.
Voyons cela avec un exemple pratique utilisant (pour faire simple)
la version française de Microsoft Excel 14.0.6123.
Créons une composante
aléatoire
basée
sur la valeur absolue d'une loi normale de moyenne 10 et d'écart-type
20 et ce sur une période de 32 mois avec la formule suivante dans
la colonne B (de B1 à B32):
=ABS(LOI.NORMALE.INVERSE.N(
ALEA.ENTRE.BORNES(0.1;10000)/10000;10;20))
où la colonne A contiendra la numérotation des périodes allant
de 1 à 32 (de A1 à A32).
Ce qui donnera une simulation d'un graphique aléatoire dont nous
allons fixer les valeurs. Par exemple:

Figure: 66.2 - Tracé d'un exemple de la fonction aléatoire avec Microsoft Excel 14.0.6123
Ensuite, ajoutons une composante de tendance (drift) linéaire
de pente 4 et d'ordonnée à l'origine de 20 à cette composante aléatoire
de manière à avoir cette fois dans la colonne B la formule suivante:
=ABS(LOI.NORMALE.INVERSE.N(
ALEA.ENTRE.BORNES(0.1;10000)/10000;10;20))+(4*A1+20)
La somme donnant graphiquement:

Figure: 66.3 - Tracé de la somme de la fonction aléatoire et la tendance
avec
Microsoft Excel 14.0.6123
Ajoutons maintenant une composante saisonnière de type sinusoïdale
avec une amplitude de 50 et une période de 12 mois et sans déphasage:

Figure: 66.4 - Tracé de la partie saisonnière seule avec Microsoft Excel 14.0.6123
La somme des trois composantes donnera dans la colonne B:
=ABS(LOI.NORMALE.INVERSE.N(
ALEA.ENTRE.BORNES(0.1;10000)/10000;10;20))+(4*A1+20)
+50*SIN(A1*2*PI()*1/12)
et graphiquement cela donne:

Figure: 66.5 - Tracé de la somme de la fonction aléatoire, la tendance
et la saisonnalité avec
Microsoft Excel 14.0.6123
et enfin ajoutons une composante cyclique qui sera encore une
fois pour l'exemple une fonction sinusoïdale d'amplitude 20 et
de période 64:

Figure: 66.6 - Tracé de la partie cyclique seule avec Microsoft Excel 14.0.6123
La somme des quatre composantes donnera dans la colonne B:
=ABS(LOI.NORMALE.INVERSE.N(
ALEA.ENTRE.BORNES(0.1;10000)/10000;10;20))+(4*A1+20)
+50*SIN(A1*2*PI()*1/12)+ 20*SIN(A1*2*PI()*1/64)
et graphiquement cela donne:

Figure: 66.7 - Somme des toutes les composantes avec Microsoft Excel 14.0.6123
Maintenant, comme nous l'avons introduit en détail dans le chapitre
de Suites Et Séries, faisons une transformée de Fourier rapide
(analyse spectrale) - abrégée TFR - avec l'Utilitaire
d'Analyse de données
intégré dans
Microsoft Excel 14.0.6123. Cela nous donne alors:

Figure: 66.8 - Tableau de la TFR avec l'Utilitaire d'analyse de Microsoft Excel 14.0.6123
Mais à la différence du chapitre de Suites Et Séries, nous allons
cette fois-ci tracer le spectre de fréquence. Pour cela, nous créons
d'abord une colonne avec une numérotation allant de 0 à 31 et juste à côté nous
mettons la formule visible dans la capture ci-dessous

Figure: 66.9 - Formules pour obtenir les fréquences dans Microsoft Excel 14.0.6123
ce qui donne:

Figure: 66.10 - Valeurs des fréquences de la TFR
Soit graphiquement pour les 16 premiers points (les autres étant
identiques par symétrie):

Figure: 66.11 - Tracé des pics de fréquence de la TFR avec Microsoft Excel 14.0.6123
Nous voyons donc que la transformée met en évidence une composante
constante (de fréquence nulle) qui est très importante. Nous pouvons
abusivement l'assimiler à la composante linéaire.
Nous voyons ensuite que trois points sortent du lot avec les
périodes respectives (inverse de la fréquence): 31 mois, 15.50,
10.33. Mais nous n'allons considérer uniquement que
les deux premières valeurs pour les associer respectivement au
cycle (ayant la plus grande période par définition) et à la saisonnalité.
Ainsi, la transformée de Fourier nous amène à considérer une
tendance constante, un phénomène cyclique ayant une période 31
mois (alors que nous avons simulé un cycle ayant une période de
64 mois...) et un phénomène saisonnier ayant une période 15 mois
(alors que nous en avions simulé un avec une période de 12 mois).
Nous voyons donc bien que ce type d'analyse a ses limites mais
qu'il peut être utile en tant qu'outil d'aide à la décision.
MODÈLES PRÉVISIONNELS DÉTERMINISTES
L'analyse de séries temporelles comporte deux grandes approches:
1. L'approche déterministe qui ne fait à la base aucunement appel
aux outils statistiques
2. L'approche statistique qui permet d'inférer sur les
prévisions
Il va de soi que la première méthode est plus simple
que la deuxième
mais que la deuxième inclut la première et est scientifiquement
parlant plus acceptable puisqu'il va être possible de définir
des intervalles de confiance.
Ces concepts généraux étant présentés
nous allons passer maintenant à la présentation de
quelques modèles mathématiques de régression
des séries temporelles. Il faut savoir à ce sujet
que:
1. Il en existe (à ma connaissance) une soixantaine
2. Certains sont déterministes, d'autres stochastiques
(ces derniers étant les meilleurs)
3. Ils sont (à ma connaissance) tous empiriques
4. Un logiciel comme Microsoft Excel suffit pour modéliser la
majorité d'entre eux
Voici la liste des noms des techniques les plus connues et utilisées
par certaines multinationales dans la pratique: Moyenne Mobile,
Single Exponential Smoothing (SES), Régression Logistique,
Méthode Linéaire de Holt, Holt-Winters, Méthode
de Brown, Stochastique Linéarisée, ARIMA, etc.
Nous allons voir ci-dessous les démonstrations
de celles qui nécessitent une démarche mathématique.
Les autres n'étant que des boîtes à outils,
elles n'ont pas leur place sur un site web tel que Sciences.ch.
Nous allons dans ce qui suit bien évidemment nous concentrer
d'abord sur les grands classiques scolaires de la première
famille de modèles.
MOYENNE MOBILE SIMPLE (LISSAGE PAR MOYENNE MOBILE)
La technique prévisionnelle de la moyenne mobile simple d'ordre k ou "Simple
Moving Average" en anglais (MA) est certainement
la technique empirique la plus simple et aussi la plus mauvaise
en termes de pouvoir prédictif. Basée sur la définition de la
moyenne mobile (cf. chapitre de Statistiques)
elle est définie par:
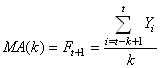 (66.14)
(66.14)
et constitue donc une prévision déterministe portant uniquement
sur une unique période ultérieure.
Voyons un exemple avec la version anglaise de Microsoft Excel 11.8346 comportant une prévision
sur l'horizon d'un mois avec des modèles de lissage par
moyenne mobile dans les colonnes D et E (comme le domaine de la
finance
est essentiellement en anglais nous ferons
toutes
les
captures
avec la version anglophone du logiciel):

Figure: 66.12 - Tableau de base pour l'exemple du lissage MA dans Microsoft Excel 11.8346
Avec donc les relations suivantes:

Figure: 66.13 - Formules pour obtenir les lissages MA(3) et MA(5) avec Microsoft Excel
11.8346
et le graphique correspondant:

Figure: 66.14 - Tracé des observations et des deux lissages avec Microsoft Excel 11.8346
Nous n'avons pas utilisé l'outil d'Utilitaire d'analyse de Microsoft Excel 11.8346 (ce dernier intégrant un outil faisant automatiquement les
calculs de la moyenne mobile) uniquement pour bien montrer au lecteur
l'application explicite des relations mathématiques données plus
haut.
Le choix du nombre de périodes k à utiliser dans le calcul
de la moyenne mobile simple dépend beaucoup des variations attendues
dans les données. Ceci peut être illustré par deux caractéristiques
de la prévision:
- Stabilité: En faisant la moyenne de plusieurs périodes, on
atténue les fluctuations aléatoires afin que la prévision soit
plus stable. La stabilité est la propriété de la prévision à ne
pas fluctuer de manière désordonnée. Gagner en stabilité est un
avantage s'il y a beaucoup de fluctuations aléatoires dans les
données. Une moyenne mobile gagnera en stabilité si un plus grand
nombre de périodes est utilisé dans le calcul de la moyenne. Un
gain en stabilité est désirable seulement jusqu'au point où les
fluctuations aléatoires sont atténuées. Si le nombre de périodes
utilisées dans le calcul de la moyenne est trop grand, la moyenne
sera tellement stable qu'elle ne répondra que trop lentement aux
changements non aléatoires de la demande.
- Réactivité: La réactivité est la propriété qu'a la prévision à s'ajuster
rapidement à un changement dans le niveau moyen réel de la demande.
L'utilisation d'une prévision réactive est appropriée dans le cas
où les fluctuations aléatoires sont faibles. Plus le nombre de
périodes utilisées dans le calcul de la moyenne mobile est petit,
plus le modèle prévisionnel sera réactif.
Remarque: Signalons que certaines
techniques de prévision font
des moyennes mobiles de moyennes mobiles... Dans la littérature
spécialisée, cela s'appelle la "moyenne
mobile double"... Il y a encore des modèles qui appliquent
des poids empiriques aux périodes passées, cela s'appelle la "moyenne
mobile pondérée" et c'est à mon avis hors d'intérêt.
MODÈLE LINÉAIRE AVEC COEFFICENTS SAISONNIERS
La technique prévisionnelle linéaire avec coefficients saisonniers
est simple à mettre en place et à comprendre. Elle
associe une simple régression linéaire (cf.
chapitre de Méthodes Numériques) et des coefficients saisonniers calculés sur
la base des valeurs passées
par rapport au modèle
linéaire. Cette technique permet de dégager des tendances en lissant
des séries chronologiques et en faisant apparaître des variations
importantes dans le temps. Les moyennes mobiles sont des moyennes
généralement calculées pour des données journalières ou hebdomadaires
et qui sont ensuite décalées période par période.
Voyons donc un exemple toujours avec Microsoft Excel 11.8346:

Figure: 66.15 - Valeurs de départ dans Microsoft Excel 11.8346 pour l'exemple
Ce qui ressemble à:

Figure: 66.16 - Graphique des ventes correspondant dans Microsoft Excel 11.8346
La première chose à faire est de déterminer l'équation de la
droite de régression (ce qui permet donc in extenso de faire aussi
de l'inférence!). Ce qui est
simple avec la méthode
des moindres carrés démontrée dans le chapitre de Méthodes Numériques
et extrêmement simple à obtenir avec les outils automatiques
intégrés à Microsoft Excel 11.8346:

Figure: 66.17 - Régression linéaire des ventes avec équations dans
Microsoft Excel 11.8346
Ce qui nous permet d'avoir deux nouvelles colonnes dans le tableau
Microsoft Excel 11.8346. Une avec les valeurs du modèle linéaire
et une autre avec le rapport entre les valeurs réelles et le modèle
linéaire
(ce qui correspond donc au coefficient saisonnier):

Figure: 66.18 - Report du modèle théorique avec rapport réel/modèle
dans Microsoft Excel 11.8346
Nous faisons ensuite une prévision sur la base de la régression
linéaire multipliée par la moyenne des coefficients saisonniers
de chaque mois. Ce que nous noterons dans le cas présent:
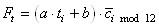 (66.15)
(66.15)
Il s'agit donc d'une méthode déterministe permettant de faire
de la prévision sur autant de périodes ultérieures que désirées
avec la possibilité de faire de l'inférence statistique si besoin
est (c'est le seul modèle déterministe sur lequel l'inférence est
directement possible).
LISSAGE EXPONENTIEL SIMPLE
La prévision 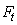 fournie
par la méthode de lissage exponentiel (EWMA pour "Exponential
Weighted Moving Average" ou SES pour "Simple Exponential
Smoothing"
en anglais), appelée
aussi "moyenne
mobile exponentielle pondérée", avec la "constante
de lissage" fournie
par la méthode de lissage exponentiel (EWMA pour "Exponential
Weighted Moving Average" ou SES pour "Simple Exponential
Smoothing"
en anglais), appelée
aussi "moyenne
mobile exponentielle pondérée", avec la "constante
de lissage" 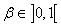 est
donnée comme nous allons le démontrer plus loin par: est
donnée comme nous allons le démontrer plus loin par:
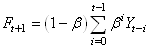 (66.16)
(66.16)
Cette définition repose sur une idée simple (mais néanmoins totalement
empirique): nous supposons que les observations influencent d'autant
moins la prévision qu'elles sont éloignées de la date t pour
laquelle nous faisons la prévision et que cette influence décroît
exponentiellement (ce modèle reste même en ce début de 21ème siècle
très utilisé pour modéliser la variance d'instruments financiers).
Nous voyons alors assez facilement dans un premier temps que:
- Plus la constante de lissage est proche de 1, plus l'influence
des observations passées remonte loin dans le temps et plus la
prévision est rigide, c'est-à-dire peu sensible aux fluctuations
conjoncturelles.
- Au contraire, plus la constante de lissage est proche de zéro,
plus la prévision est influencée par les observations récentes
(prévision souple).
Démontrons dans un tout premier temps que la définition précédente
s'écrit sous une autre forme moins technique qui est la plus commune
dans les livres de statistiques:
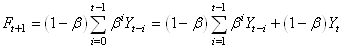 (66.17)
(66.17)
et nous avons aussi in extenso:
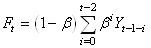 (66.18)
(66.18)
Dès lors si nous réindexons la somme nous retrouvons une écriture
très connue dans le monde de la finance (mesure de volatilité du
modèle RiskMetrics):
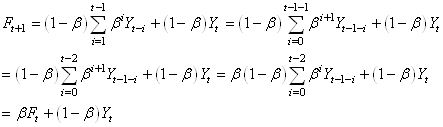 (66.19)
(66.19)
La prévision 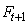 apparaît
donc comme une moyenne pondérée entre la prévision apparaît
donc comme une moyenne pondérée entre la prévision 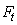 faite à la
date t et la dernière observation faite à la
date t et la dernière observation 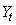 ,
le poids donné à cette dernière observation étant d'autant plus
fort que la constante de lissage est faible. ,
le poids donné à cette dernière observation étant d'autant plus
fort que la constante de lissage est faible.
Nous allons démontrer maintenant pourquoi les logiciels projettent
les modèles EWMA avec une espérance égale à la dernière valeur
mesurée:
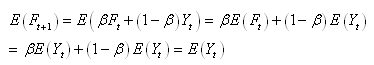 (66.20)
(66.20)
En pratique, le choix de la constante de lissage est souvent
fondé sur des critères subjectifs de rigidité ou de souplesse de
prévision. Il existe cependant une méthode plus objective qui consiste
à déterminer des outils de recherche opérationnelle
(cf.
chapitre de Méthodes Numériques), la constante qui minimise
la somme des carrés des erreurs de prévisions.
Attention!!! Dans la majorité des ouvrages de statistiques contemporains,
la constante de lissage est définie comme étant:
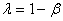 (66.21)
(66.21)
Il vient alors:
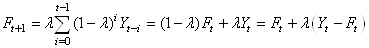 (66.22)
(66.22)
écriture qui amène à considérer le lissage exponentiel simple
comme une bête moyenne mobile pondérée.
L'une et l'autre des écritures sont bien sûr équivalentes mais
il faut sur certains logiciels faire attention de bien savoir à laquelle
des deux constantes de lissage nous avons affaire... Nous allons
continuer personnellement avec cette dernière forme pour la suite
de nos développements.
Maintenant, repartons de la relation précédente pour l'écrire
sous une autre forme en utilisant la récursivité:
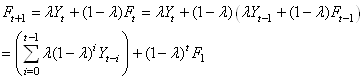 (66.23)
(66.23)
Montrons maintenant que la somme des poids est égale à l'unité afin
de constater qu'il s'agit bien d'une pondération. Nous avons
donc:
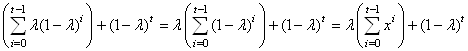 (66.24)
(66.24)
Nous avons démontré dans le chapitre de Suites Et Séries que:
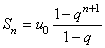 (66.25)
(66.25)
Il vient alors dans notre exemple:
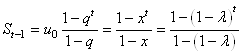 (66.26)
(66.26)
Donc:
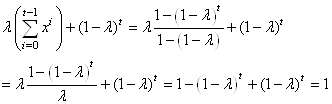 (66.27)
(66.27)
Enfin, parlons de l'origine du nom de cette technique. Nous avons
donc:
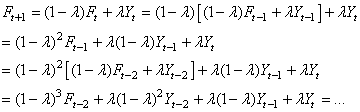 (66.28)
(66.28)
Nous y retrouvons:
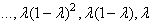 (66.29)
(66.29)
et comme 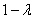 est
strictement inférieur à l'unité, les facteurs est
strictement inférieur à l'unité, les facteurs 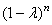 décroissent
de manière exponentielle (il suffit de représenter graphiquement
la fonction): décroissent
de manière exponentielle (il suffit de représenter graphiquement
la fonction):
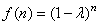 (66.30)
(66.30)
pour le constater avec 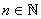 . .
Ceci étant fait, parlons du problème des valeurs initiales. Nous
avons donc:
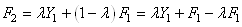 (66.31)
(66.31)
Il est alors de convention de prendre:
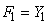 (66.32)
(66.32)
Ce qui nous donne:
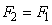 (66.33)
(66.33)
Raison pour laquelle un logiciel comme Microsoft Excel 11.8346 nous
retournera pour 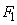 l'erreur
#N/A. l'erreur
#N/A.
Pour la suite il est nécessaire que nous étudiions l'origine
de l'expression du lissage exponentiel simple. L'idée à la base
des mathématiciens était de réduire l'erreur entre la valeur réelle 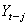 et
la prévision considérée comme constante a: et
la prévision considérée comme constante a:
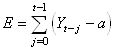 (66.34)
(66.34)
mais le but était aussi d'affaiblir les erreurs plus petites
que l'unité et d'amplifier celles qui en étaient plus grandes en
élevant les écarts au carré tels que:
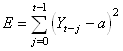 (66.35)
(66.35)
et enfin de pondérer celles qui étaient éloignées dans le temps
de la prévision par un coefficient tel que nous ayons à minimiser
au final:
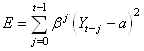 (66.36)
(66.36)
En prenant la dérivée de E par rapport à a, et
en l'annulant il vient:
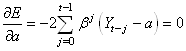 (66.37)
(66.37)
Nous obtenons alors pour 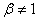 : :
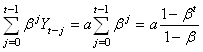 (66.38)
(66.38)
et donc au final:
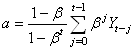 (66.39)
(66.39)
et pour t grand il vient:
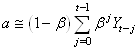 (66.40)
(66.40)
Nous retrouvons donc la relation définie au début de l'étude
de ce modèle et qui était:
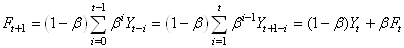 (66.41)
(66.41)
Il est à noter qu'il n'est pas du tout évident que la constante
recherchée qui minimise l'erreur puisse être utilisée comme fonction
de prévision. Cependant c'est l'usage qu'il en est fait par de
nombreux praticiens... Certains spécialistes
préfèrent
noter ce dernier résultat sous la forme (il ne faut pas chercher
à trop comparer cette notation avec celle de la relation précédente):
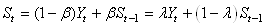 (66.42)
(66.42)
où S fait référence au "S" qu'il y a dans le
mot "eStimé". Il y a même des logiciels de statistiques
qui proposent à notre étonnement de faire une prévision à un
temps 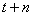 en
se basant sur cette méthode... ce qui nous semble un peu limite
limite... (affaire à suivre). en
se basant sur cette méthode... ce qui nous semble un peu limite
limite... (affaire à suivre).
Remarque: Le lissage exponentiel simple a été suggéré en premier
par Charles C. Holt en 1957, mais la formulation (forme de la relation
prévisionnelle) est attribuée à Brown. Il s'agit d'une technique
que l'on retrouve implémentée dans la quasi-totalité des logiciels
de statistiques.
 Exemple: Exemple:
Nous voulons donc appliquer:
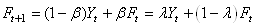 (66.43)
(66.43)
Considérons le tableau suivant (la colonne C contient déjà le
modèle mathématique dont nous allons détailler les
formules juste après):

Figure: 66.19 - Données de départ avec modèle de lissage exponentiel
dans Microsoft Excel 14.0.6123
Nous n'allons pas utiliser l'outil d'Utilitaire d'analyse de
Microsoft Excel 14.0.6123 (ce dernier intégrant un outil faisant
automatiquement les calculs du lissage exponentiel simple) uniquement
pour bien
montrer au lecteur l'application explicite des relations mathématiques
démontrées plus haut. De plus l'Utilitaire d'analyse de Microsoft
Excel 14.0.6123 souffre d'un gros défaut: il demande la valeur de la constante
de lissage plutôt que d'en calculer une valeur optimale automatiquement.
Il n'y a que trois colonnes qui ont des formules, le reste étant
des saisies statiques. Nous avons:

Figure: 66.20 - Formules correspondantes au modèle de lissage exponentiel simple
avec Microsoft Excel 14.0.6123
où le lecteur attentif aura remarqué la prévision à la ligne
28 sur un horizon de un mois.
Avec un peu plus loin dans la feuille les valeurs indispensables à l'optimisation du modèle
avec le solveur que nous allons de suite voir: 
Figure: 66.21 - Constante de lissage et indicateurs d'erreur pour optimiser le modèle
avec
Microsoft Excel 14.0.6123
Maintenant, nous allons utiliser le solveur pour minimiser soit
l'erreur MAPE, soit l'erreur MAD ou enfin l'erreur MSD. Nous avons
alors par exemple en minimisant l'erreur MAPE:

Figure: 66.22 - Paramétrage du solveur avec Microsoft Excel 14.0.6123
Ce qui donne le résultat suivant:

Figure: 66.23 - Solution proposée par le solveur de Microsoft Excel 14.0.6123
Soit graphiquement:

Figure: 66.24 - Tracé de la comparaison des observations et du modèle
SES avec
Microsoft Excel 14.0.6123 (sans la prévision)
et donc le tableau de valeurs devient:

Figure: 66.25 - Tableau correspondant après optimisation avec le solveur dans
Microsoft
Excel 14.0.6123
et nous voyons donc la prévision à la ligne 28 du tableau
qui vaut:
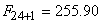 (66.44)
(66.44)
Pour clore, indiquons que si nous faisons l'hypothèse
forte que pour tout temps t:
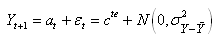 (66.45)
(66.45)
Alors dans le cas d'une série infinie (ou supposée
comme telle...):
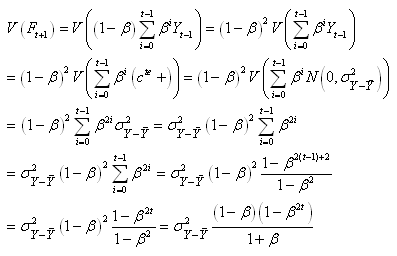 (66.46)
(66.46)
Or, comme 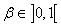 et
si t est suffisamment grand, il vient: et
si t est suffisamment grand, il vient:
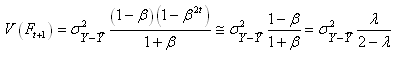 (66.47)
(66.47)
et considérons l'erreur:
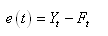 (66.48)
(66.48)
Nous avons sous l'hypothèse que les deux termes
soustraits sont indépendants...:
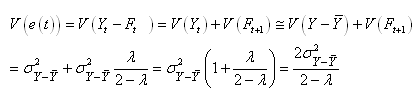 (66.49)
(66.49)
Il s'ensuit sous l'hypothèse de Normalité (ce
qui est le cas depuis le début de ce développement)
et que 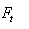 est
l'espérance de est
l'espérance de 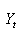 : :
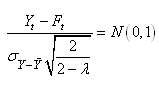 (66.50)
(66.50)
et dons sous l'hypothèse que la variance est parfaitement
connue, il vient:
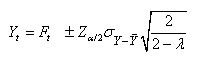 (66.51)
(66.51)
Mais si l'écart-type est seulement estimé,
il faut
évidemment utiliser la loi de Student (cf.
chapitre de Statistiques):
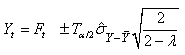 (66.52)
(66.52)
Et ce sera tout en ce qui concerne le modèle
de lissage exponentiel simple.
LISSAGE EXPONENTIEL DOUBLE À UN PARAMÈTRE (MÉTHODE DE BROWN)
L'idée du lissage exponentiel double (DEBS: "Double Exponential
Brown Smoothing" en anglais) est à nouveau
de réduire
l'erreur totale mais cette fois-ci en utilisant non pas une simple
constante mais une droite au voisinage de t telle que:
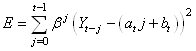 (66.53)
(66.53)
ce qui est écrit traditionnellement (le est absorbé dans le
paramètre a et le fait que les paramètres de la droite
soient recalculés à chaque t est omis afin de ne pas le
confondre avec l'indice de sommation...):
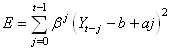 (66.54)
(66.54)
Pour minimiser nous différencions E:
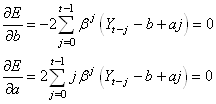 (66.55)
(66.55)
d'où:
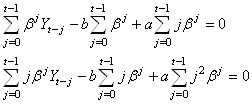 (66.56)
(66.56)
Simplifions tout cela en remplaçant d'abord lorsque t est
grand:
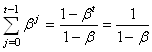 (66.57)
(66.57)
Pour les autres, sous certaines conditions qui sont respectées
dans notre cas, nous pouvons dériver terme à terme une série convergente
pour obtenir la dérivée de celle-ci. Ainsi, étant donné que:
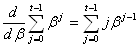 (66.58)
(66.58)
et vu que dans les conditions susmentionnées:
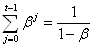 (66.59)
(66.59)
nous avons alors immédiatement:
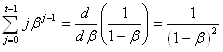 (66.60) .
(66.60) .
En multipliant par 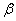 à gauche
et à droite nous obtenons au final: à gauche
et à droite nous obtenons au final:
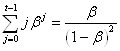 (66.61)
(66.61)
qui est la deuxième simplification recherchée.
Pour la troisième il suffit de dériver encore une fois l'égalité précédente.
Nous obtenons alors:
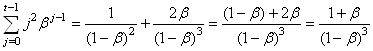 (66.62)
(66.62)
Et nous terminons en multipliant à gauche et à droite par 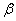 : :
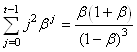 (66.63)
(66.63)
Nous obtenons alors:
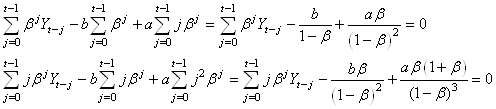 (66.64)
(66.64)
Ce que nous pouvons écrire sous la forme:
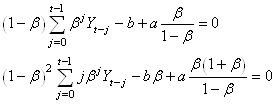 (66.65)
(66.65)
Définissons la série lissée:
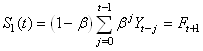 (66.66)
(66.66)
et la série doublement lissée (d'où le nom de la technique...):
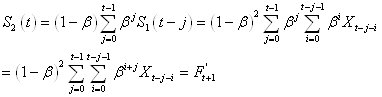 (66.67)
(66.67)
Après le changement de variable 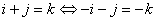 nous
obtenons: nous
obtenons:
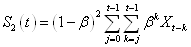 (66.68)
(66.68)
L'indice de la deuxième somme s'expliquant par le fait que k est
la nouvelle variable d'indexation (donc elle doit forcément être
dans l'indice!) et quand i est nul nous avons:
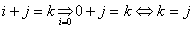 (66.69)
(66.69)
Pour le suffixe de la somme il s'explique par le fait que pour
la valeur maximale nous avons 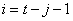 et
donc comme et
donc comme 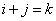 ,
il vient si nous y substituons i: ,
il vient si nous y substituons i:
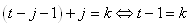 (66.70)
(66.70)
Ensuite, le lecteur vérifiera lui-même.... sur papier que nous
pouvons réarranger
les termes de la manière suivante:
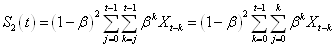 (66.71)
(66.71)
Nous avons alors:
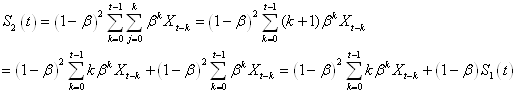 (66.72)
(66.72)
En substituant ces résultats dans:
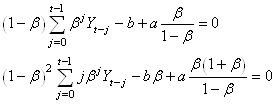 (66.73)
(66.73)
il vient:
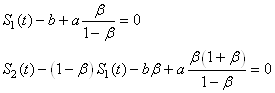 (66.74)
(66.74)
Il vient alors après simplification successives:
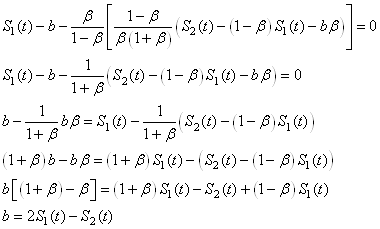 (66.75)
(66.75)
et donc aussi après simplifications successives:
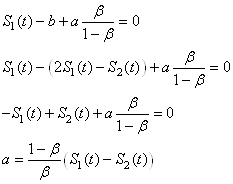 (66.76)
(66.76)
Résultats qu'il est d'usage de noter:
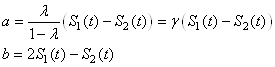 (66.77)
(66.77)
Donc:
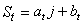 (66.78)
(66.78)
est la droite constituée d'un double lissage exponentiel qui
approche au mieux (l'estimé) à un temps t les données
réelles et qui minimise l'erreur totale. Contrairement au lissage
exponentiel simple, nous pouvons par contre maintenant faire des
prévisions (cependant cela reste un usage abusif du résultat mathématique)
de par la présence de la variable j.
Explicitement, cette droite s'écrira en changeant un peu les
notations (ne pas oublier qu'au début nous avions implicitement
injecté un signe négatif dans le terme a):
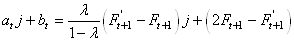 (66.79)
(66.79)
Il vient donc que notre prévision s'écrira:
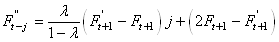 (66.80)
(66.80)
Et évidemment, si nous voulons 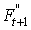 ,
il faudra choisir ,
il faudra choisir 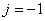 .
Dès lors: .
Dès lors:
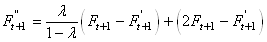 (66.81)
(66.81)
Pour débuter les prévisions avec ce modèle, il faut un estimé de 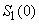 et et 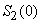 .
Les premières prévisions seront grandement affectées par ces estimés.
Il faut aussi toujours vérifier ce que les logiciels utilisent
comme méthode de détermination pour ces premiers paramètres afin
de la spécifier dans les rapports. .
Les premières prévisions seront grandement affectées par ces estimés.
Il faut aussi toujours vérifier ce que les logiciels utilisent
comme méthode de détermination pour ces premiers paramètres afin
de la spécifier dans les rapports.
Remarque: Le lissage exponentiel de
Brown est rarement intégré dans
les logiciels statistiques. On lui préfère le modèle de Holt que
nous allons de suite voir après et qui le contient implicitement.
 Exemple: Exemple:
Considérons le tableau suivant dans Microsoft Excel 14.0.6123 qui contient les
données observées dans la colonne B ainsi que le modèle dans les
colonnes C à F dont nous allons détailler les formules juste après:

Figure: 66.26 - Données de départ avec modèle de lissage exponentiel
double de Brown
dans Microsoft Excel 14.0.6123
Indiquons les formules pour les C, D, E, F, G (H et I étant
les mêmes que pour le lissage exponentiel simple). Il vient alors:

Figure: 66.27 - Formules correspondantes au modèle de lissage de Brown
avec Microsoft Excel 14.0.6123
Avec un peu plus loin dans la feuille les valeurs indispensables à l'optimisation
du modèle avec le solveur que nous allons de suite voir:

Figure: 66.28 - Constante de lissage et indicateurs d'erreur pour optimiser le modèle
avec Microsoft Excel 14.0.6123
La procédure pour minimiser soit l'erreur MAPE, soit l'erreur
MAD ou enfin l'erreur MSD avec le solveur est exactement la même
que pour le lissage exponentiel simple! Nous ne la détaillerons
donc pas.
Le résultat donnera graphiquement (et aussi en
comparaison avec le lissage exponentiel simple):

Figure: 66.29 - Tracé de la comparaison des observations et du modèle
SES/DEBS
avec Microsoft Excel 14.0.6123 (avec la prévision)
Nous voyons que le lissage double est meilleur que le lissage
simple (son MAPE minimisé étant de 6.90% contre 7.89% pour le lissage
simple). Cette comparaison est pour rappel une forme de "back-testing".
La projection à la
25ème
période
est par contre très
proche.
Ce qui est ensuite intéressant et particulier avec le lissage
exponentiel double est de jouer avec la valeur de j. Ainsi,
en imposant 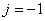 ,
nous aurons pour chaque valeur de la colonne G, sa projection à la
période correspondante à sa ligne plus ,
nous aurons pour chaque valeur de la colonne G, sa projection à la
période correspondante à sa ligne plus 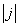 périodes. Évidemment,
pour les deux premières lignes, les projections ne sont pas à prendre
en considération! périodes. Évidemment,
pour les deux premières lignes, les projections ne sont pas à prendre
en considération!
Faisons un petit exemple visuel. En posant 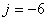 (donc
projection à six mois...) nous avons alors: (donc
projection à six mois...) nous avons alors:

Figure: 66.30 - Projection avec le modèle DEBS dans Microsoft Excel 14.0.6123
Ainsi, nous pouvons observer qu'au quatrième mois (période),
le modèle donne une projection de 168.04 pour le dixième mois (période)
et qu'en réalité il y a eu 180. Nous voyons un exemple d'une très
mauvaise projection du modèle le sixième mois (période) où le modèle
donne une projection de 139.65 alors qu'en réalité il y a eu 171...
Ensuite, ce qui est intéressant c'est de se rappeler que si nous
posons 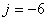 ,
la 20ème période, projette alors pour 26ème, la 21ème sur
la 27ème, etc. Nous obtenons alors graphiquement: ,
la 20ème période, projette alors pour 26ème, la 21ème sur
la 27ème, etc. Nous obtenons alors graphiquement:

Figure: 66.31 - Projection sur un horizon de un semestre en utilisant le DEBS
avec
Microsoft Excel 14.0.6123
Évidemment, comme tout modèle, il faut être
très
prudent avec des projets à 6 mois car le modèle ne
prend pas en compte les facteurs de la bourse, des catastrophes
naturelles,
des pandémies, des guerres, etc. Donc tant qu'il y n'a pas
d'inférence
statistique, il n'est pas possible de donner un intervalle de
confiance pour la prévision ce qui est scientifiquement
parlant pas vraiment acceptable.
LISSAGE EXPONENTIEL DOUBLE À 2 PARAMÈTRES DE HOLT (MODÈLE
ADDITIF)
Nous allons présenter ici une technique dont la construction
est empirique et qui est due à Charles C. Holt (1957).
Même
dans l'article d'origine de Holt il n'y a pas de démonstration
rigoureuse de la construction de ce modèle. Il s'agit donc plus
d'ingénierie
mathématique que de mathématique pure à proprement parler (donc
la présentation de ce modèle n'aurait normalement pas lieu d'être
présente sur ce site Internet).
L'idée est la suivante comme pour le modèle précédent, d'avoir
un modèle de la forme:
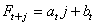 (66.82)
(66.82)
mais avec une approche empirique qui consiste à s'imposer que:
- La pente 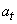 de
la droite du modèle dont l'origine du repère est en t sera
obtenue par lissage exponentiel simple de toutes les pentes des
droites précédentes. de
la droite du modèle dont l'origine du repère est en t sera
obtenue par lissage exponentiel simple de toutes les pentes des
droites précédentes.
- L'ordonnée à l'origine 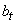 de
la droite en t sera obtenue par lissage exponentiel
simple de toutes les ordonnées à l'origine des droites précédentes. de
la droite en t sera obtenue par lissage exponentiel
simple de toutes les ordonnées à l'origine des droites précédentes.
Rappelons d'abord que nous avions obtenu pour le lissage exponentiel
simple:
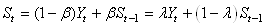 (66.83)
(66.83)
Il est clair que la pente de chaque droite de l'estimé est donnée
par (voir figure ci-dessous):
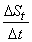 (66.84)
(66.84)
et pour le dernier estimé, plus spécifique, nous aurons:
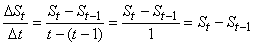

Figure: 66.32 - Schéma du principe de base de construction du modèle
et l'idée étant de faire un lissage exponentiel de la pente de
toutes les droites dont la pente se calcule de la même manière,
soit (à comparer à l'expression du lissage exponentiel simple):
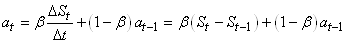 (66.85)
(66.85)
Cette dernière expression est souvent appelée "estimé de
la pente à la période t".
Maintenant, pour l'ordonnée à l'origine, nous remarquons sur
la figure que 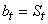 .
Dès lors, il vient dans un premier temps que: .
Dès lors, il vient dans un premier temps que:
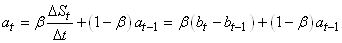 (66.86)
(66.86)
Une fois ce constat fait, nous choisissons un modèle où l'ordonnée à l'origine
est un lissage exponentiel de toutes les ordonnées à l'origine
avec sa propre constante de lissage précédente tel que:
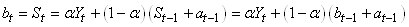 (66.87)
(66.87)
Ce qui peut paraître parfois déroutant ici, c'est la dernière
parenthèse. Au fait, techniquement, on devrait plutôt l'écrire:
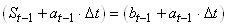 (66.88)
(66.88)
mais comme le 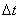 est
toujours égal à 1, nous omettons son écriture. Donc la dernière
parenthèse représente l'estimé à une unité de temps précédente à laquelle
on ajoute l'accroissement d'une unité de temps de la pente de l'estimé au
même temps t. est
toujours égal à 1, nous omettons son écriture. Donc la dernière
parenthèse représente l'estimé à une unité de temps précédente à laquelle
on ajoute l'accroissement d'une unité de temps de la pente de l'estimé au
même temps t.
L'expression:
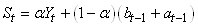 (66.89)
(66.89)
est un peu malheureusement appelée dans la pratique "estimé du
niveau de la série à la période t".
Au final, nous travaillons avec les trois relations:
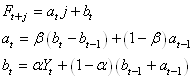 (66.90)
(66.90)
Pour débuter les prévisions avec ce modèle, il faut un estimé de 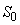 et
de et
de 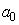 .
Les premières prévisions seront grandement affectées par ces estimés.
Il faut aussi toujours vérifier ce que les logiciels utilisent
comme méthode de détermination pour ces premiers paramètres afin
de la spécifier dans les rapports. .
Les premières prévisions seront grandement affectées par ces estimés.
Il faut aussi toujours vérifier ce que les logiciels utilisent
comme méthode de détermination pour ces premiers paramètres afin
de la spécifier dans les rapports.
 Exemple: Exemple:
Considérons le tableau suivant dans Microsoft Excel 14.0.6123 qui contient les
données observées dans la colonne B ainsi que le
modèle dans les colonnes C à F dont nous allons détailler
les formules juste après:

Figure: 66.33 - Données de départ avec modèle de lissage exponentiel
double de Holt
dans Microsoft Excel 14.0.6123
Indiquons les formules pour les C, D, E (G et H étant les mêmes
que pour le lissage exponentiel simple). Il vient alors:

Figure: 66.34 - Formules correspondantes au modèle de lissage exponentiel de Holt
avec
Microsoft Excel 14.0.6123
Avec un peu plus loin dans la feuille les valeurs indispensables à l'optimisation
du modèle avec le solveur que nous allons de suite voir:

Figure: 66.35 - Constante de lissage et indicateurs d'erreur pour optimiser le modèle
avec
Microsoft Excel 14.0.6123
La procédure pour minimiser soit l'erreur MAPE, soit l'erreur
MAD ou enfin l'erreur MSD avec le solveur est exactement la même
que pour le lissage exponentiel simple! Nous ne la détaillerons
donc pas.
Ce qui donne graphiquement (et aussi en comparaison avec le lissage
simple et double):

Figure: 66.36 - Projection sur un horizon de un semestre en utilisant le modèle
de Holt
avec
Microsoft Excel 14.0.6123
Le lissage de Holt a un MAPE de 7.38% alors que celui de Brown à un
MAPE de 7.12% (cette comparaison est pour rappel une forme de "back-testing").
Cependant l'avantage du modèle de Holt est qu'on
peut faire des projections à plus d'une période.
Il est bien évidemment intéressant de comparer les projections à six
mois entre la méthode additive de Holt et le lissage de Brown:

Figure: 66.37 - Comparaison entre modèle de Brown et Holt additif
Nous voyons donc que le modèle de Holt a
presque toujours des valeurs de projection supérieures au
modèle
de Brown.
Il convient avant de juger ces valeurs de les comparer
aux observations qui
seront constatées dans l'avenir.
LISSAGE EXPONENTIEL TRIPLE À 3 PARAMÈTRES DE HOLT ET
WINTERS (MODÈLE MULTIPLICATIF)
Nous allons présenter ici une technique dont la construction
est elle aussi empirique et qui est fortement inspirée du modèle
de lissage exponentiel double de Holt. Je n'ai jamais trouvé de
démonstration rigoureuse de ce modèle. Il s'agit donc probablement
aussi plus d'ingénierie mathématique que de mathématique pure à proprement
parler mais comme c'est un classique dans les logiciels de statistiques,
nous allons nous attarder dessus un petit moment.
Winters (étudiant de Holt) s'est basé en 1960
sur la méthode de son professeur pour définir un modèle qui prend
en considération la composante saisonnière. L'idée consiste à utiliser
trois équations de lissage: une pour le niveau de la demande (désaisonnalisée),
une pour la tendance et une pour la saisonnalité.
Remarque: Il existe deux méthodes de Winters selon que la saisonnalité est
additive ou multiplicative. Nous ne présentons ici que le modèle
multiplicatif car c'est celui le plus couramment utilisé. Et puis
nous ne pouvons pas présenter tous les modèles existants car ils
sont tous empiriques et il en existe des centaines voire probablement
des milliers!
Soit N, le nombre de périodes dans chaque cycle saisonnier
(cycle supposé constant!). Trois équations de lissage exponentiel
sont utilisées à chaque période pour actualiser les estimés de
la série désaisonnalisée, les facteurs saisonniers et la tendance.
Ces équations peuvent avoir différentes constantes de lissage notées
traditionnellement  , , 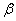 et et 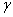 . .
La première équation est définie assez naturellement par:
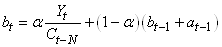 (66.91)
(66.91)
où 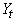 est
alors le niveau actuel de la série désaisonnalisée par le
facteur saisonnier approprié est
alors le niveau actuel de la série désaisonnalisée par le
facteur saisonnier approprié 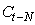 (nous
retrouvons sinon la méthode de Holt). (nous
retrouvons sinon la méthode de Holt).
La deuxième équation est elle aussi naturellement définie par:
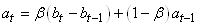 (66.92)
(66.92)
où nous retrouvons donc la pente de la tendance identiquement
au modèle de Holt.
La troisième équation est totalement nouvelle, ce qui n'empêche
pas qu'elle est relativement intuitive et est donnée par:
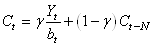 (66.93)
(66.93)
et finalement la prévision est resaisonnalisée (c'est la forme
de la prévision qui fait que nous parlons de "modèle
multiplicatif"):
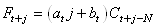 (66.94)
(66.94)
Cette dernière équation assume que 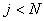 .
Si .
Si 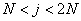 ,
le facteur saisonnier approprié serait ,
le facteur saisonnier approprié serait 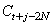 .
Si .
Si 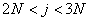 ,
le facteur saisonnier approprié serait ,
le facteur saisonnier approprié serait 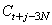 et
ainsi de suite. et
ainsi de suite.
Donc au final, nous avons le système:
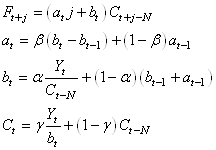 (66.95)
(66.95)
Pour débuter les prévisions avec ce modèle, il faut aussi un
estimé des paramètres initiaux. Encore une fois, les premières
prévisions seront grandement affectées par ces estimés. Il faut
aussi toujours vérifier ce que les logiciels utilisent comme méthode
de détermination pour ces premiers paramètres afin de la spécifier
dans les rapports.
 Exemple: Exemple:
Considérons le tableau suivant dans Microsoft Excel 14.0.6123
qui contient les données observées dans la colonne
D ainsi que le modèle dans les colonnes E à H dont
nous allons détailler
les formules juste après (ici, nous avons N qui vaut
zéro
donc). Remarquez que nous avons 6 années avec chacune 4 trimestres
(donc in extenso il y aura 4 coefficients saisonniers qui sont les
4 premières lignes de la colonne G):

Figure: 66.38 - Données de départ avec modèle de lissage exponentiel
triple de Holt
et Winters
dans Microsoft Excel 14.0.6123
Indiquons les formules pour les E, F, G, H (I et J étant les
mêmes que pour le lissage exponentiel simple). Il vient alors:

Figure: 66.39 - Formules correspondantes au modèle de lissage exponentiel de Holt
et Winters
avec Microsoft Excel 14.0.6123
Avec un peu plus loin dans la feuille les valeurs indispensables à l'optimisation
du modèle avec le solveur que nous allons de suite voir:

Figure: 66.40 - Constante de lissage et indicateurs d'erreur pour optimiser le modèle
avec
Microsoft Excel 14.0.6123
La procédure pour minimiser soit l'erreur MAPE, soit l'erreur
MAD ou enfin l'erreur MSD avec le solveur est exactement la même
que pour le lissage exponentiel simple! Nous ne la détaillerons
donc pas.
Ce qui donne graphiquement (et aussi en comparaison avec le lissage
simple, double et le modèle additif de Holt):

Figure: 66.41 - Projection sur un horizon de un semestre en utilisant le modèle
de Holt et Winters
avec
Microsoft Excel 14.0.6123
Le lissage de Holt avait donc un MAPE de 7.38% et celui de Brown à un
MAPE de 7.12%. Le lissage saisonnier de Holt et Winters a un MAPE
de 9.61%. Cependant l'avantage du modèle de Holt et Winters est
qu'on peut faire des projections à plus d'une période avec cycles
ainsi que nous pouvons le voir sur le graphique.
Il est bien évidemment intéressant de comparer les projections à 6
mois entre la méthode additive de Holt et le lissage de Brown:

Figure: 66.42 - Comparaison entre modèle de Brown, et Holt additif et Holt et
Winters
Donc nous voyons encore une fois qu'en fonction de la technique
choisie, les différences sont relativement importantes.
RÉGRESSION LOGISTIQUE
Il arrive toujours dans les entreprises que dans l'analyse d'un
produit ou d'un service, que celui-ci voie son nombre de ventes
croître, ensuite passer par un point d'inflexion et ensuite
aller vers une asymptote pour diminuer à nouveau par la
suite avec une caractéristique similaire.
Le modèle logistique permettant de simuler un tel comportement
dans le cadre de l'analyse des séries temporelles (à ne
pas confondre avec la régression logistique vue dans le
chapitre de Méthodes Numériques!) est défini
ainsi:
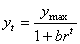 (66.96)
(66.96)
Il s'inspire de nombreux modèles que nous retrouvons
en physique et où 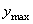 est
le seuil de saturation (asymptote horizontale) qui peut être déterminé suite à un
audit du marché et son % de pénétration. est
le seuil de saturation (asymptote horizontale) qui peut être déterminé suite à un
audit du marché et son % de pénétration.
Remarque: Il faut aussi savoir que
ce modèle est bien meilleur que celui utilisé par
le lissage exponentiel compris dans l'Utilitaire d'Analyse de Microsoft
Excel 14.0.6123 (même si comme nous l'avons vu mathématiquement,
ils ne fonctionnent absolument pas sur les mêmes bases).
Une simple observation comparative des résultats obtenus
suffit à s'en rendre compte.
b et r sont eux deux paramètres du modèle
tels que:
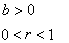 (66.97)
(66.97)
le point d'inflexion est toujours donné par le cumul de
50% du seuil de saturation. Le résultat est alors une courbe
en S du type suivant:

Figure: 66.43 - Comparaison mesures avec modèle logistique
où en jaune a été représenté les données
actuelles d'une entreprise et en bleu le modèle théorique
prévisionnel associé.
Pour déterminer l'équation de la courbe logistique,
nous pouvons utiliser directement les solveurs de certains logiciels.
Mais ceux-ci ont parfois besoin d'avoir des données de départ
proches de la valeur théorique. Nous allons donc d'abord
montrer comment ces valeurs de départ peuvent être déterminées
avec un exemple.
Considérons le tableau suivant fait avec Microsoft Excel
11.8346 (les ventes sont en centaines de milliers d'unités):

Figure: 66.44 - Ventes en fonction des semaines
et le graphique associé:

Figure: 66.45 - Tracé des mesures précédentes
qui pourrait être jugé comme linéaire
suivant le moment auquel débute l'analyse
descriptive des ventes dans l'entreprise.
Pour déterminer le modèle théorique, nous
allons linéariser l'équation logistique en
utilisant un seuil hypothétique (objectifs de ventes du
marché)
de 800.
Donc:
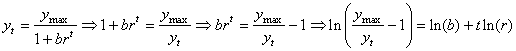 (66.98)
(66.98)
Soit à calculer la nouvelle variable à expliquer:
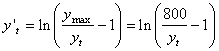 (66.99)
(66.99)
et nous écrirons le modèle linéaire correspondant:
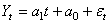 (66.100)
(66.100)
avec donc:
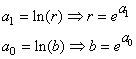 (66.101)
(66.101)
Soit:
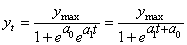 (66.102)
(66.102)
Dans notre exemple, la régression linéaire (cf.
chapitre de Méthodes Numériques) donne:
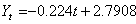 (66.103)
(66.103)
soit:
Nous avons alors immédiatement:
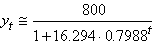 (66.104)
(66.104)
Soit sous forme graphique:

Figure: 66.46 - Comparaison mesures avec modèle logistique
avec ce modèle formel, nous avons une somme des carrés
des écarts entre les mesures et le modèle (cf.
chapitre de Statistiques) de:
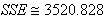 (66.105)
(66.105)
Maintenant, entrons ces données dans Microsoft Excel 14.0.6123
sous la forme suivante:

Figure: 66.47 - Comparaison mesures et valeurs du modèle théorique
avec la structure suivante:

Figure: 66.48 - Formules explicites pour le calcul du modèle théorique
Si nous lançons le solveur de Microsoft Excel 14.0.6123
avec les paramètres
suivants (nous avons mis 0.0001 comme plus petite valeur puisque
le solveur ne propose pas de relation d'ordre stricte):

Figure: 66.49 - Paramètres du solveur pour minimiser SSE
Ce qui donne:

Figure: 66.50 - Résultat du solveur
Soit:
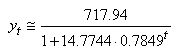 (66.106)
(66.106)
avec:
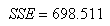 (66.107)
(66.107)
soit nettement inférieur à notre approche utilisant
la régression linéaire et donc meilleur. Effectivement
voyons le tableau de résultat:

Figure: 66.51 - Valeurs données par le modèle obtenu par optimisation
et graphiquement cela donne:

Figure: 66.52 - Comparaison entre mesures, modèle par régression et modèle
par optimisation
Nous voyons nettement que le modèle du solveur (modèle
numérique) est meilleur que le modèle formel donné par
une régression linéaire et il est aussi meilleur
comme déjà mentionné que le lissage exponentiel
proposé par l'Utilitaire d'analyse de Microsoft Excel 11.8346!
Pour en finir avec ces modèles de prévisions, rappelons que ceux-ci
doivent être suivis régulièrement pour s'assurer que le modèle
et les paramètres utilisés sont toujours appropriés. Comme le lecteur
l'aura peut-être deviné, un modèle de prévision ne doit pas avoir
de biais. La somme des erreurs doit donc voisiner zéro, avec parfois
des surestimations et parfois des sous-estimations. Lorsque le
modèle a tendance à toujours surestimer (ou sous-estimer), ce dernier
a un biais et il doit être révisé.
Afin de détecter que le modèle est biaisé, on fera typiquement
le suivi de la différence entre la prévision et l'observation sur
une carte de contrôle (cf. chapitre de Génie
Industriel).
Il faut aussi pour conclure rappeler qu'il existe une différence
parfois importante entre les valeurs observées (ventes effectives)
et les observations qu'il y aurait eu réellement si l'offre était
infinie. Effectivement, les ventes observées ne prennent pas en
compte les ventes ratées parce que faute de stock dans une des
milliers de succursales que possède votre entreprise, un client
est allé voir chez la concurrence. Ainsi, les ventes observées
sont toujours un "minimum" faute des ventes loupées!
Remarque: Indiquons qu'il est
aussi trivialement possible de faire la différence de tous
les points consécutifs dans le temps d'une série
temporelle et ensuite de faire un histogramme pour déterminer
la loi de probabilité des fluctuations, ce qui permet de
faire de l'inférence statistique avec toutes les précautions
nécessaires.
MODÈLES AUTORÉGRESSIFS
Dans l'étude d'une série chronologique, il est naturel
de penser que la valeur de la série à la date t peut dépendre
en partie des valeurs
prises aux dates précédentes:
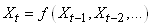 (66.108)
(66.108)
ce qui évidemment est une écriture limitée à une
série univariée
(nous n'étudierons par les séries multivariées),
discrète, et dont la fréquence d'échantillonage
est constante (au contraire que ce qui se fait dans dans certains
domaines des
transactions
financières).
Nous avons vu dans le chapitre de Probababilité que lorsque
nous nous tenons uniquement à une dépendance avec
l'instant t-1,
nous parlons alors de "chaîne de Markov", ou plus
rigoureusement de "chaîne de Markov
d'ordre 1".
Avant de continuer, ouvrons un paranthèse sur l'intérêt
des chaînes de Markov (rappel
orienté finance)...
Considérons
que nous avons des valeurs boursières à une fréquence
fixe (par exemple journalière ou horaire... peu importe!).
Il est alors très aisé de calcul la proportion de
Augmentations (A) versus
les Diminutions (D) des valeurs d'intérêt.
Ainsi, en prenant en compte l'ensemble de l'historique, nous aurons
typiquement un tableau
du genre (les valeurs proviennent des indices du S&P 500 entre
1947 et 2007):
|
Proportion Augmentations (A) |
Proporitions
Diminutations (D) |
Total |
|
0.474 |
0.526 |
1 |
Tableau: 66.1 - Proportion de variations A/D sur l'ensemble d'un historique
Mais bon cela ne sera pas vraiment à grand chose... Si
nous compliquons un peu l'analyse en nous demandant quelle proportion
nous avons deux augmentations
successives (AA), diminutions successives (DD),
ou alternance (DA) et (AD) dans l'ensemble de
l'historique cela double le travail et pourrait nous donner typiquement
un tableau du genre:
|
(A) |
(D) |
Total |
|
0.519 |
0.481 |
1 |
(A) |
0.433 |
0.567 |
1 |
Tableau: 66.2 - Proportion de variations A/D sur l'ensemble par rapport à la période
précédente
Les valeurs ci-dessus peuvent donc bien évidemment
être vues commes les probabilités conditionnelles:
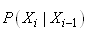 (66.109)
(66.109)
Et si maintenant nous faisons une analyse non pas
que sur la période précédente mais sur les deux dernières, cela
signifie que nous calculons les proportions des séquences
(DDD),
(DDA), (DAD), (DAA), (ADD),
(ADA), (AAD), (AAA) et cela double encore
une fois le nombre de calculs:
| |
|
|
|
|
|
(A) |
(D) |
Total |
(D) |
(D) |
0.501 |
0.499 |
1 |
(D) |
(A) |
0.412
|
0.588
|
1
|
(A) |
(D) |
0.539 |
0.461 |
1 |
(A) |
(A) |
0.449 |
0.551 |
1 |
Tableau: 66.3 - Proportion de variations A/D sur l'ensemble par rapport à 2 périodes
précédentes
Les valeurs ci-dessus peuvent donc bien évidemment être
vues commes les probabilités conditionnelles:
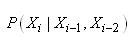 (66.110)
(66.110)
Nous voyons donc qu'en ajoutant à chaque fois une période
précédente
supplémentaire à l'analyse, nous doublons le nombre
de calculs. Ainsi, en prenant les 20 dernières périodes,
cela nous amène à
près de 1 millions de probabilités conditionnelles
(proportions). Nous comprenons alors tout l'intérêt
de nous restreindre à un faible
nombre de valeurs antérieures ou a une seule valeur comme
le font les chaînes de Markov. Ainsi, la probabilité que la séquence
des 4 prochains jours soit AADA sera sans hypothèse simplificatrice:
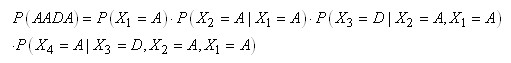 (66.111)
(66.111)
mais se réduira dans
l'hypothèse d'une chaîne de Markov (c'est-à-dire
une dépendance
seulement avec
la période précédente) à:
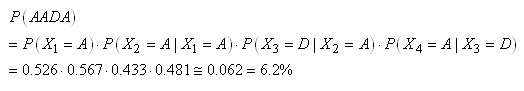 (66.112)
(66.112)
Savoir si le modèle de probabilités conditionnelles
totales ou la version simplifié de Markov est un vaste débat.
L'hypothèse
de la marche aléatoire (implicitement: le modèle
de Markov) est défendue par une majorité d'économistes...
mais cette hypothèse
à bien évidemment aussi un certain nombre de condradicteurs.
Il n'est généralement pas nécessaire de prendre en compte tout
le passé de la série ou seulement le dernier événement
et nous pouvons le plus souvent nous limiter à p valeurs:
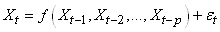 (66.113)
(66.113)
où 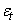 est
un bruit blanc est
un bruit blanc 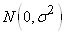 ou
processus de Wiener noté parfois WN. Plus rigoureusement,
et pour des raisons d'application de techniques statistiques, un
bruit
blanc est défini par: ou
processus de Wiener noté parfois WN. Plus rigoureusement,
et pour des raisons d'application de techniques statistiques, un
bruit
blanc est défini par:
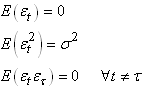 (66.114)
(66.114)
La seule différence par rapport au mouvement
brownien standard c'est que comme nous le verrons plus loin, il
y a ici la présence
d'un facteur d'inertie noté traditionnellement 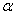 dans
les cas simples qui
influence fortement la dynamique du processus tel que: dans
les cas simples qui
influence fortement la dynamique du processus tel que:
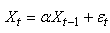 (66.115)
(66.115)
Effectivement, comme
il est très facile de le faire dans Microsoft Excel conformément à la
procédure indiquée lors de notre étude des processus de Wiener:
Voici différents tracés de la série temporelle en fonction de
quelques valeurs du facteur d'inertie:

Figure: 66.53 - Processus autorégressif d'ordre 1
Si nous considérons 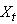 comme
une variable aléatoire spécifique (ayant une fonction
de densité donnée)
que nous noterions X et comme
une variable aléatoire spécifique (ayant une fonction
de densité donnée)
que nous noterions X et 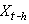 comme
une autre variable aléatoire spécifique (ayant une
fonction de densité donnée) que nous noterions Y,
alors rien ne nous empêche étant connues les fonctions de
densité de chacune de ces
variables, de calculer leur covariance: comme
une autre variable aléatoire spécifique (ayant une
fonction de densité donnée) que nous noterions Y,
alors rien ne nous empêche étant connues les fonctions de
densité de chacune de ces
variables, de calculer leur covariance:
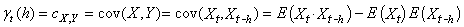 (66.116)
(66.116)
Par exemple, dans la pratique nous connaissons souvent les espérances 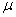 des
deux variables aléatoires aux deux moments différents
ainsi que quelques-unes des valeurs de leurs distributions sous-jacentes
(réalisations aléatoires). Alors, il devient aisé de
calculer leur covariance. Mais ce n'est pas un indicateur vraiment
utile. Rien
ne nous empêche en supposant une relation linéaire d'utiliser
le coefficient de corrélation
linéaire: des
deux variables aléatoires aux deux moments différents
ainsi que quelques-unes des valeurs de leurs distributions sous-jacentes
(réalisations aléatoires). Alors, il devient aisé de
calculer leur covariance. Mais ce n'est pas un indicateur vraiment
utile. Rien
ne nous empêche en supposant une relation linéaire d'utiliser
le coefficient de corrélation
linéaire:
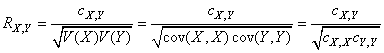 (66.117)
(66.117)
Mais qui se note alors traditionnellement et trivialement dans
le cas des séries temporelles:
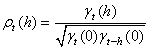 (66.118)
(66.118)
et est appelé "coefficient
d'autocorrélation" souvent abrégé dans
les logiciels de statistiques ACF.
Personnellement je préfère réécrire la relation
précédente sous la forme explicite suivante (la covariance
est explicitée):
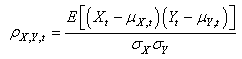 (66.119)
(66.119)
Il faut savoir que lorsque nous faisons de l'analyse
de séries temporelles, dans la pratique, nous comparons
souvent une suite avec elle-même mais comportant un décalage
temporel h. L'autocorrélation d'ordre h est
donc la corrélation entre la série et elle-même retardée de h relevés.
Ainsi, puisque les deux suites sont dépendantes
et ont les mêmes caractéristiques statistiques, nous écrivons
dans ce cas particulier dit de "processus
stationnaire du second ordre" la relation suivante appelée "coefficient
d'autocorrélation empirique":
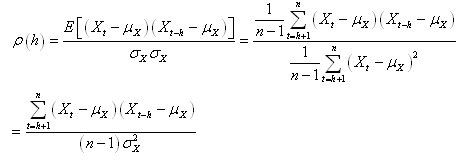 (66.120)
(66.120)
où évidement il ne faut pas oublier que dans la
pratique l'espérance
et l'écart-type ne sont que des estimateurs bien que cela
ne soit pas explicite dans la définition ci-dessus puisque le domaine
de l'analyse temporelle n'indique
que très rarement les petites chapeaux au-dessus des estimateurs
(contrairement à ce que nous avons fait dans le chapitre
de Statistiques).
Évidemment dans le cas de l'analyse de séries
temporelles où nous soupçonnons une cyclicité,
la valeur la plus grande de 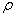 pour
un h donné indique la fréquence
(respectivement la périodicité) de la cyclicité sous-jacente à la
série ce qui peut aider par exemple pour le choix du type
de moyenne mobile (voir plus bas). pour
un h donné indique la fréquence
(respectivement la périodicité) de la cyclicité sous-jacente à la
série ce qui peut aider par exemple pour le choix du type
de moyenne mobile (voir plus bas).
Définition: Nous appelons "corrélogramme", le
diagramme représentant les coefficients d'autocorrélatioon
d'ordre 1, 2, 3, ..., h, ... de la série.
Remarque: Il existe différentes variantes de cette relation
dans certains logiciels. Il peut arriver d'obtenir des petites
différences numériques par rapport à l'utilisation
de la relation ci-dessus.
Voici par exemple une famille de séries temporelles:

Figure: 66.54 - Quelques exemples de séries temporelles
avec leur corrélogramme
correspondant avec bien évidemment pour différentes
valeurs de h en abscisse et la valeur de 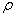 en
ordonnée: en
ordonnée:

Figure: 66.55 - Corrélogrammes correspondants
Faisons un exemple pratique de calcul de corrélogramme
avec Microsoft Excel 14.0.6123 et des données fictives:

Figure: 66.56 - Données avec moyenne et coefficients d'autocorréation
Il suffit alors dans la cellule D3 d'écrire la relation
générale pour tout h (j'ai pas trouvé plus
simple à ce jour et qui soit parfaitement juste...)
=(SOMME((DECALER($A$4:$A$23;0;0;NB($A$4:$A$23)-E4)
-DECALER($B$4:$B$23;0;0;NB($B$4:$B$23)-E4))
*(DECALER($A$4:$A$23;E4;0;NB($A$4:$A$23)-E4)
-DECALER($B$4:$B$23;E4;0;NB($B$4:$B$23)-E4)))
/((ECARTYPE($A$4:$A$23)^2)*(NB($A$4:$A$23)-1)))
et donc le corrélogramme correspondant:

Figure: 66.57 - Corrélogramme correspondant à l'exemple
Définitions:
D1. Une série temporelle
est dite "stationnaire
au sens faible" ou plus simplement un "processus
stationnaire faible" si le premier (espérance)
et second (variance) moment existent, sont finis et constants
dans le temps (donc ne dépendant pas du temps):
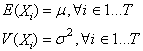 (66.121)
(66.121)
La première condition (constance de l'espérance) élimine
donc toute tendance. Si la fonction de densité sous-jacente à chaque 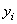 est
une loi Normale, alors nous parlons de "processus
Gaussien".
D2. Si nous avons N séries temporelles non stationnaires
et que leur somme pondérée (la somme des poids étant égal
comme
à l'habitude à l'unité): est
une loi Normale, alors nous parlons de "processus
Gaussien".
D2. Si nous avons N séries temporelles non stationnaires
et que leur somme pondérée (la somme des poids étant égal
comme
à l'habitude à l'unité):
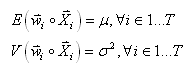 (66.122)
(66.122)
donne une processus stationnaire faible,
nous disons alors que les séries
temporelles
sont "cointégrées".
Ceci est utile en finance pour pouvoir avec certains instruments
non stationnaires fabriquer un portefeuille dont le rendement
l'est (pour des raisons de traitement de mathématique).
Remarque: Certains auteurs rajoutent
à la définition des processus stationnaires faibles que ceux-ci
doivent avoir une covariance qui existe, soit finie et indépendante
des instants choisis, ou plus exactement ne dépende que
de l'écart
entre les instants choisis, c'est-à-dire:

Considérons un cas important dans de nombreuses entreprises sur
certaines périodes plus ou moins longues. Soit:
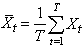 (66.123)
(66.123)
la moyenne temporelle. Si 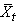 converge
en probabilité vers converge
en probabilité vers 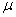 quand quand 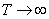 nous
disons que le processus est "ergodique
pour la moyenne".
Donc quand nous
disons que le processus est "ergodique
pour la moyenne".
Donc quand 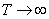 : :
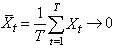 (66.124)
(66.124)
PROCESSUS AUTORÉGRESSIFS AR(p)
Présentons le concept de processus autorégressif en introduisant
le cas particulier de processus autorégressif d'ordre 1, noté AR(1)
et défini par la relation (à une constante additive près):
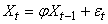 (66.125)
(66.125)
Il s'agit donc d'une chaîne de Markov d'ordre 1 (nous pouvons
toujours vérifier dans la pratique si le modèle obtenu est à posteriori
avec des résidus gaussiens ou non!).
Nous disons que le processus autorégressif AR(1) est stationnaire
si nous avons à toute date t:
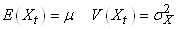 (66.126)
(66.126)
En toute généralité, nous avons:
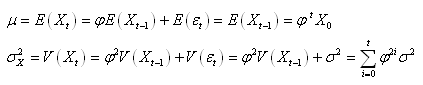 (66.127)
(66.127)
et donc la stationnarité implique obligatoirement que (se rappeler
que la constante additive a été posée comme
nulle dans la définition
ci-dessus, dans le cas contraire cela change les conclusions ci-dessous):
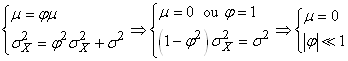 (66.128)
(66.128)
Donc la stationnarité implique in extenso les deux résultats
utiles:
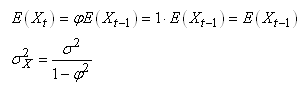 (66.129)
(66.129)
Il est intéressant de remarquer que la variance est
indépendante du temps et donc qu'elle ne diverge pas. Cependant,
il ne faut pas considérer
cela comme forcément
positif car il n'est pas très cohérent dans la pratique
que la volatilié soit constante (processus homoscédastique).
Raison pour laquelle nous aborderons des modèles plus complexes
dont la volatilité est dépendante du temps.
Remarquons aussi
que pour que la variance soit toujours positive (par définition
de la variance) il faut que 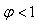 . .
Voyons ce que l'hypothèse de stationnarité implique et pour cela,
nous allons d'abord avoir besoin de l'égalité suivante:
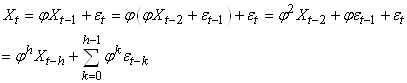 (66.130)
(66.130)
Donc in extenso:
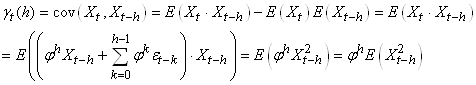 (66.131)
(66.131)
Et rappelons la relation de Huyghens (cf.
chapitre de Statistiques):
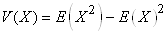 (66.132)
(66.132)
Il vient alors:
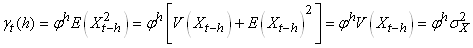 (66.133)
(66.133)
Donc l'autocorrélation vaut:
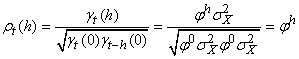 (66.134)
(66.134)
Puisque la stationnarité implique que 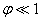 ,
les corrélogrammes (ACF) des processus AR(p) auront des
allures décroissantes
amorties: le processus oublie en quelque sorte les valeurs passées. ,
les corrélogrammes (ACF) des processus AR(p) auront des
allures décroissantes
amorties: le processus oublie en quelque sorte les valeurs passées.
Nous
avons aussi pour un processus AR(1) stationnaire avec constante
(offset):
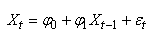 (66.135)
(66.135)
l'espérance suivante:
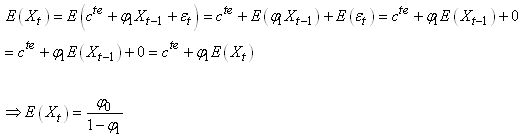 (66.136)
(66.136)
Donc si la constante est nulle nous retrouvons bien une espérance
nulle comme démontré plus haut. La variance aura
la même expression
que celle déjà démontrée plus haut,
c'est-à-dire:
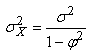 (66.137)
(66.137)
puisque l'ajout d'une constante ne change rien à la variance
de la série. Nous avons donc obtenu ci-dessus l'espérance
et la variance (inconditionnelles) d'un processus AR(1).
Si, 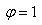 nous
avons alors le processus AR(1) qui s'écrit: nous
avons alors le processus AR(1) qui s'écrit:
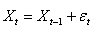 (66.138)
(66.138)
qui n'est dès lors donc par construction pas stationnaire. La
non stationnarité est courante dans la pratique et pose problèème
pour faire des analyses. Il existe dès lors une astuce pour rendre
stationnaires certaines séries non-stationnaires et faire des manip
dessus et ensuite les rendre à nouveau non stationnaires par la
procédure inverse.
Ainsi, en ce qui concerne l'AR(1) avec 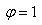 ,
l'idée est d'utiliser ce que l'on appelle la "propriété
d'intégration"
d'une série temporelle. Ainsi, l'AR(1) est une série intégrée
d'ordre 1, désignée par I(1) car si on la différencie d'une unité
temporelle, nous obtenons alors une série stationnaire: ,
l'idée est d'utiliser ce que l'on appelle la "propriété
d'intégration"
d'une série temporelle. Ainsi, l'AR(1) est une série intégrée
d'ordre 1, désignée par I(1) car si on la différencie d'une unité
temporelle, nous obtenons alors une série stationnaire:
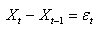 (66.139)
(66.139)
Ce qui s'écrit avec "l'opérateur retard" L:
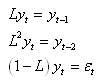 (66.140)
(66.140)
Et donc une série est ingérée d'ordre 2 s'il faut la "différencier"
deux fois pour la rendre stationnaire.
Un processus AR(2) est un processus autorégressif qui vérifie
une relation de la forme (à une constante additive près):
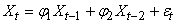 (66.141)
(66.141)
Donc dans un tel modèle, l'influence du passé se manifeste par
une régression linéaire sur les deux valeurs antérieures. Selon
les valeurs de 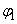 et et 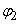 il
n'est pas toujours possible de trouver un processus stationnaire
vérifiant cette dernière relation. il
n'est pas toujours possible de trouver un processus stationnaire
vérifiant cette dernière relation.
En général, un processus AR(p) est un processus qui dépend
linéairement des p valeurs antérieures (à une constante
additive près):
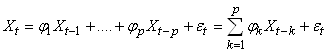 (66.142)
(66.142)
PROCESSUS AUTORÉGRESSIFS MA(q)
D'abord une mise en garde. Il ne faut pas confondre ce processus
stationnaire avec les moyennes mobiles. En effet, le terme n'est
pas très bien choisi car s'il y a bien mobilité (ce qui est la
moindre des choses de la part d'un processus), il est abusif de
parler de moyenne...
Nous sommes en fait dans le cadre d'une chronique de prévisions
qui montrent des erreurs autocorrélées mais rien d'autre (au fait
cela servira pour un mélange un peu plus loin).
Présentons le concept de processus autorégressif de moyenne mobile
en introduisant le cas particulier de processus autorégressif de
moyenne mobile d'ordre 1, noté MA(1) et défini par la relation:
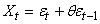 (66.143)
(66.143)
Pour un tel processus, nous avons par définition du bruit blanc:
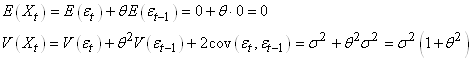 (66.144)
(66.144)
Donc les deux moments sont indépendants du temps est nous
avons affaire à un processus stationnaire faible. Cependant,
il ne faut pas considérer cela comme forcément positif
car il n'est pas très cohérent dans la pratique que
la volatilié soit constante (processus homoscédastique).
Raison pour laquelle nous aborderons des modèles plus complexes
dont la volatilité est
dépendante du temps.
En ce qui concerne l'autocorrélation, nous avons d'abord (ne
pas oublier de revoir les trois conditions qui définissent le bruit
blanc et particulièrement la troisième):
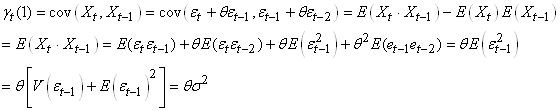 (66.145)
(66.145)
Le coefficient d'autocorrélation d'ordre 1 vaut donc:
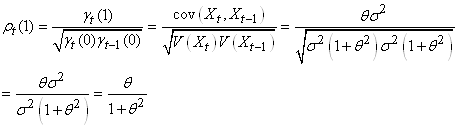 (66.146)
(66.146)
Pour 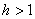 ,
nous avons immédiatement en faisant le même développement que: ,
nous avons immédiatement en faisant le même développement que:
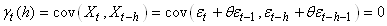 (66.147)
(66.147)
donc les coefficients d'autocorrélations d'ordre supérieur à 1
sont tous nuls!
Un processus MA(2) est un processus autorégressif qui vérifie
une relation de la forme:
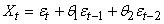 (66.148)
(66.148)
Et nous pouvons réitérer les mêmes développements que pour MA(1)
avec enthousiasme... pour arriver aussi à la conclusion que l'autocorrélation
(ACF) est nulle pour 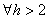 . .
En général, un processus MA(q) est un processus qui dépend
linéairement des q valeurs antérieures:
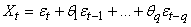 (66.149)
(66.149)
et donc pour un tel processus on peut admettre sans faire la
démonstration générale que:
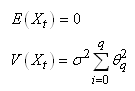 (66.150)
(66.150)
et que l'autocorrélation est nulle pour 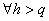 .
Ainsi, on peut facilement reconnaître un processus MA(q)
car son ACF présente un "cut-off" à partir de q. .
Ainsi, on peut facilement reconnaître un processus MA(q)
car son ACF présente un "cut-off" à partir de q.
PROCESSUS ARMA
Nous pouvons bien évidemment envisager de combiner les deux modèles
précédents (MA(q) et AR(p)) en introduisant:
- Une dépendance du processus vis-à-vis de son passé avec un
processus AR(p)
- Un effet retard des aléas avec un processus MA(q)
Un tel modèle, appelé "autorégressif-moyenne
mobile non saisonnier" ou "ARMA
non saisonnier",
est caractérisé par le paramètre p de la partie autorégressive
et le paramètre q de la partie moyenne mobile.
Ainsi, un processus ARMA(p, q) non saisionner
vérifie
la relation:
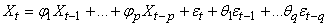 (66.151)
(66.151)
Le principal avantage des processus ARMA non saisonniers
tient au fait qu'ils permettent de fournir des prévisions
pour des échéances
éloignées (du moins plus éloignée dans
le temps que la prochaine date). Effectivement, rappelons que pour
les processus AR(1), nous avons obtenu:
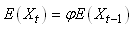 (66.152)
(66.152)
Nous avons alors:
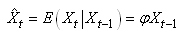 (66.153)
(66.153)
Soit in extenso:
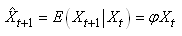 (66.154)
(66.154)
Les prévisions s'obtiennent ensuite de manière
récursive:
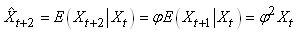 (66.155)
(66.155)
Et donc d'une façon plus générale:
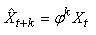 (66.156)
(66.156)
et donc lors k devient très grand, nous
avons alors:
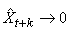 (66.157)
(66.157)
Autrement dit, pour un ordre k élevée,
le moèle AR(1) se contente de fournir comme espérance
conditionnelle la prévision la moyenne (historique)
du processus. Quand l'espérance conditionnelle est nulle, nous disons
alors dans le domaine des séries temporelles que "l'espérance
est orthogonale à tout
passé".
Donc comme noous puvons le voir, les processus ARMA
ont une espérance qui a une mémoire de type exponentiellement décroissante
à cause du facteur 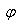 qui
est à la puissance k dans la relation antéprécédente.
Alors qu'un processus de type MA seul a une fonction qui coupe
sec la mémoire dans temporielle à une valeur q (cut-off
de q périodes). Ces deux processus sont donc considérés
comme à mémoire courte. qui
est à la puissance k dans la relation antéprécédente.
Alors qu'un processus de type MA seul a une fonction qui coupe
sec la mémoire dans temporielle à une valeur q (cut-off
de q périodes). Ces deux processus sont donc considérés
comme à mémoire courte.
PROCESSUS ARIMA
Les modèles de séries chronologiques vus précédemment sont en
réalité que des cas particuliers d'un modèle général empirique
que l'on appelle les modèles "ARIMA" pour "AutoRegressive
Integrated Moving Average" connus aussi sous le nom
de "technique de Box-Jenkins".
Cette technique présuppose que la série chronologique est générée
par un processus aléatoire (brownien ou autre) et que les valeurs
futures sont liées aux erreurs passées.
Cependant ce modèle a une limitation importante, et le fait que
l'on retrouve à travers cette généralisation les lissages exponentiels
signifie que ceux-ci ont aussi la même limitation: la série chronologique
doit être stationnaire. Donc pour rappel, cela signifie que les
moments comme l'espérance ou la variance et l'autocorrélation doivent être
constants dans le temps.
Un modèle ARIMA est souvent classifié sous la notation:

où p est le nombre de termes autorégressifs, d le
nombre de différences non-saisonnales et q le nombre
de termes d'erreurs dans l'équation de prédiction. Voici quelques
exemples:
- Moyenne: ARIMA(0,0,0) avec constante
- Naif: ARIMA(0,1,0)
- Drift: ARIMA(0,1,0) avec constante
- ARMA: ARIMA(1,0,1)
- Lissage exponentiel simple:
ARIMA(0,1,1)
- Lissage exponentiel
double de Holt: ARIMA(0,2,2)
- Lissage exponentiel
de Holt-Winters (multiplicatif): pas d'équivalent ARIMA à ma connaissance
- Lissage exponentiel
de Holt-Winters (additif): SARIMA(0,1,m+1)(0,1,0)
Revenons un peu sur les techniques de projection (prédiction)
des modèles ARIMA. Commençons par un cas partiulièrement
simple (c'est
à notre avis plus pédagogique) en considérant
le processus noté AR(1)
et défini
pour rappel par la la relation (à une constante additive
près):
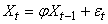 (66.158)
(66.158)
Lorsque nous faisons l'estimation ponctuelle d'une
projection de ce modèle, sur l unités de temps
ultérieures, il est d'usage de
noter
la valeur ponctuelle estimée par différentes notations d'usage:
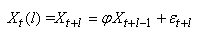 (66.159)
(66.159)
où 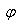 est
bien évidemment supposé avoir été detérminé à l'aide
des valeurs historiques connues. Cependant, l'estimation ponctuelle
projetée est... justement une estimation!!!! Il nous faudrait
donc connaître son espérance. L'hypothèse naïve
la plus simple est alors d'utiliser l'espérance conditionnelle
de la valeur projetée, qui nous avait mené (voir
juste plus haut) au résultat: est
bien évidemment supposé avoir été detérminé à l'aide
des valeurs historiques connues. Cependant, l'estimation ponctuelle
projetée est... justement une estimation!!!! Il nous faudrait
donc connaître son espérance. L'hypothèse naïve
la plus simple est alors d'utiliser l'espérance conditionnelle
de la valeur projetée, qui nous avait mené (voir
juste plus haut) au résultat:
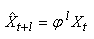 (66.160)
(66.160)
qui tend donc vers 0 quand l tend vers l'infini comme
nous l'avons déjà mentionné. Mais n'oubliez
pas que ce modèle AR(1)
est défini à une constante additive près (qui
est souvent la moyenne arithmétique ou la médiane
des valeurs connues de la série
temporelle), donc dans le cas général cela tend vers
une constante.
Au passage, observons que nous avons explicitement
l'erreur de prévision qui est donnée par:
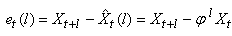 (66.161)
(66.161)
Et rappelons que nous avons démontré plus
haut que pour les AR(1):
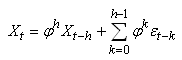 (66.162)
(66.162)
Et considérons h (respectivement l) grand
et 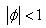 , nous avons alors: , nous avons alors:
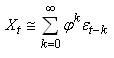 (66.163)
(66.163)
Adapté à notre contexte de notation:
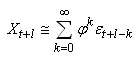 (66.164)
(66.164)
Soit, un processus 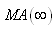 . Alors: . Alors:
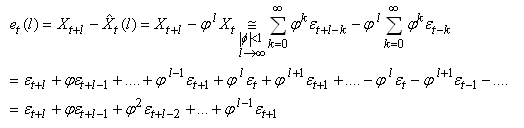 (66.165)
(66.165)
Nous remarquons donc que l'erreur de projection 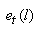 est
un processus du type est
un processus du type 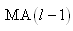 .
Il vient alors de façon immédiate de ce dernier développement: .
Il vient alors de façon immédiate de ce dernier développement:
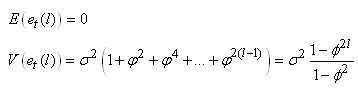 (66.166)
(66.166)
où la somme des carrées a été simplifiée
en utilisant un résultat démontré dans le
chapitre de Suites Et Séries. Nous voyons ainsi que la variance
de l'erreur de prévision ne diverge pas (du moins dans le
cas d'un AR(1)) et tend vers une valeur finie (ce qui n'est pas
le cas de tous les processus) quand l tend
vers l'infini à condition
que 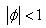 .
La difficulté dans la pratique étant
de choisir une technique pour déterminer .
La difficulté dans la pratique étant
de choisir une technique pour déterminer 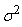 (il
en existe une quantité: adéquation, Monte-Carlo,
Boostrapping, bayésienne, etc.!).
Raison pour laquelle il ne faut jamais se limiter à l'utilisation
d'un seul logiciel statistique pour faire des projections mais au
moins à trois
différents. (il
en existe une quantité: adéquation, Monte-Carlo,
Boostrapping, bayésienne, etc.!).
Raison pour laquelle il ne faut jamais se limiter à l'utilisation
d'un seul logiciel statistique pour faire des projections mais au
moins à trois
différents.
Pourquoi revenir là-dessus penserez-vous peut-être???
Pour la simple raison qu'il nous faut un intervalle
statistique de prédiction. Ainsi, étant donné que
nous avons un estimateur ponctuel 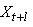 qui
est la réalisation de la variable aléatoire de la
valeur projetée et son espérance associée qui
est la réalisation de la variable aléatoire de la
valeur projetée et son espérance associée 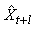 ,
nous pouvons écrire: ,
nous pouvons écrire:
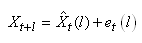 (66.167)
(66.167)
Et faire l'hypothèse à la vue des développement précédents
que l'erreur de prévision suit une loi Normale centrée:
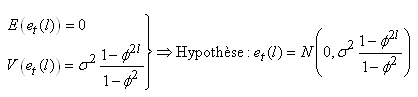 (66.168)
(66.168)
Nous avons alors à un seuil de confiance donné si 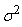 est
parfaitement déterminé: est
parfaitement déterminé:
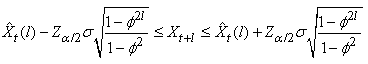 (66.169)
(66.169)
et si nous n'avons qu'un estimateur de 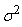 alors
nous prendrons (cf. chapitre de Statistiques): alors
nous prendrons (cf. chapitre de Statistiques):
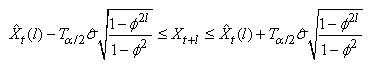 (66.170)
(66.170)
La pratique de ces modèles de projections tendrait
à montrer qu'ils sous-estiment le risque (la variance). Donc plutôt
que de prendre un intervalle à 95% il vaut peut-être mieux prendre
un intervalle plus élevé en fonction du retour sur expérience.

- Calculs commerciaux et bancaires, J.-Ch.
Corbaz + D. Goetschi, Collection C.C.L
- Théorie de la spéculation,
L. Bachelier, Éditions Jacques Gabay, ISBN10: 2876471299
(148 pages) - Réimprimé en 1995
- Théorie Financière, R.
Cobbaut, Éditions
Economica, ISBN10: 2717834427
(560 pages) - Imprimé en
2005
- The mathematics of financial derivates,
P. Wilmott + S. Howison, Éditions Cambridge, ISBN10:
0521497892 (317 pages) - Imprimé en
1997
- Finance des marchés, Techniques
quantitatives et applications pratiques, S. Bossu,
P. Henrotte, Éditions Dunod, ISBN13:
9782100518128 (274 pages) - Imprimé en
2008
- Mastering Financial Modelling in
Microsoft Excel, Éditions Prentice Hall,
Alastair L. Day, ISBN13: 9780273643104 (370
pages) - Imprimé en
2001
- Financial Risk Manager Handbook, Éditions
GARP, Philippe Jorion, ISBN13: 9780471217633
(749 pages) - Imprimé en
2009
- Options, Futures and other derivates, Éditions
Pearson, John Hull, ISBN13: 9782744075339 (850 pages)
- Imprimé en
2011
|