|

ASTRONOMIE | ASTROPHYSIQUE | RELATIVITÉ RESTREINTE
RELATIVITÉ GÉNÉRALE | COSMOLOGIE | THÉORIE
DES CORDES
Dernière mise à jour de ce chapitre:
2017-12-31 17:56:19 | {oUUID 1.728}
Version: 3.1 Révision 13 | Avancement: ~90%
 vues
depuis le 2012-01-01: 0 vues
depuis le 2012-01-01: 0
 LISTE DES SUJETS TRAITÉS SUR CETTE PAGE
LISTE DES SUJETS TRAITÉS SUR CETTE PAGE
Comme
nous l'avons vu dans le chapitre précédent, la
relativité restreinte
est une réussite remarquable d'un point de vue théorique
aussi bien que d'un point de vue pratique en formant
un continuum d'espace-temps où les
grandeurs d'espace et de temps se voient
donner la même dimension physique (celle d'une distance
métrique pour rappel!). Cependant, celle-ci s'applique
aux repères
euclidiens seulement et aux référentiels
inertiels/Galiléens
(à vitesse constante pour rappel... ). Il convient donc
de généraliser
l'ensemble de la mécanique d'abord en exprimant ses
principes et ses résultats fondamentaux sous une forme
généralisée indépendante
du type de systèmes de coordonnées choisi (in
extenso: du type d'espace) en faisant usage du calcul tensoriel
et ensuite de prendre en
compte les systèmes non inertiels. L'équivalence
des systèmes
inertiels par le relativité restreinte et la non-équivalence
des systèmes non inertiels peut être donc résumé (un
peu sommairement...) en disant que la vitesse est relative mais
l'accélération est
absolue. Ainsi, nous ne pouvons jamais distinguer le repos d'un
mouvement uniforme, mais nous pouvons distinguer ceux-ci d'un
mouvement accéléré.
Il
convient aussi de prendre en compte que le fait que
la relativité
restreinte ne s'applique qu'aux référentiels
Galiléens est restrictif
car toute masse crée un champ gravitationnel dont la
portée est
infinie. Pour pouvoir trouver un vrai référentiel
galiléen, il est
donc nécessaire de se situer infiniment loin de toute
masse. La mécanique relativiste bâtie à partir
de la relativité restreinte
ne constitue donc qu'une approximation des lois de la nature,
dans
le cas où les champs gravitationnels ou les accélérations
sont suffisamment faibles. Cette limitation d'application
n'est plus adaptée à l'astrophysique relativiste
dont l'activité
s'est intensifiée à la fin du 20ème siècle.
C'est ici qu'encore une
fois intervient Albert Einstein et nombre de ses confrères
à travers le temps!
POSTULATS ET PRINCIPES
Einstein
croyait
en une physique ne devant privilégier aucun référentiel
puisque telle
était à ses yeux la réalité de l'Univers
(nous en avons déjà
fait mention). Mais comment se soustraire alors au phénomène
d'accélération?
L'idée géniale fut d'énoncer le "postulat
d'équivalence" ci-dessous (qui encore
aujourd'hui en ce début
du 21ème siècle n'est toujours pas pris en défaut
par les expériences
récentes) en plus du postulat d'invariance et du principe
cosmologique que nous avons énoncés dans le
chapitre de Relativité Restreinte et de l'hypothèse
selon laquelle le mouvement d'une particule qui ne subit
aucune autre
interaction
que la
gravitation est une ligne géodésique (voir plus
loin la démonstration).
POSTULAT
D'ÉQUIVALENCE
Dans un premier temps, Albert
Einstein va améliorer le postulat d'équivalence
dont les versions les plus anciennes sont dues à Galilée
et à Newton:
Postulat: L'accélération (uniforme!) d'une masse
(hors champ gravitationnel) due à l'application d'une
force mécanique et l'accélération de cette
même masse soumise à un champ gravitationnel (uniforme!)
sont supposées
parfaitement équivalentes. Ainsi, les résultats
des analyses mathématiques
dans un cas, peuvent s'appliquer dans l'autre (déjà là c'est
fort mais cohérent... l'idée est très
très bonne encore fallait-il l'avoir...!)
Autrement dit, le champ
de gravité possède une propriété fondamentale qui le distingue
de tous les autres champs connus dans la nature: le mouvement
de chute libre des corps est universel, indépendant de la masse
et de la composition des corps.
Corollaire: La masse au
repos d'un corps doit alors être la même qu'elle soit
mesurée
dans un référentiel dans un champ gravitationnel
ou hors champ gravitationnel (nous parlons
alors
de masse inertielle
et de masse pesante comme nous l'avons vu au tout début
de notre
étude de la mécanique classique).
Remarque: Il faut bien prendre garde et vérifier
que le corollaire du postulat d'équivalence soit vrai
sinon toute la relativité générale
s'écroulerait (en ce début de 21ème siècle
des expériences sont
toujours en cours pour essayer de mettre en défaut
cette équivalence)!
Donc tout champ de
gravitation statique et uniforme est équivalant à un
référentiel
accéléré dans le vide. Nous pouvons physiquement
considérer tout champ de gravitation comme
statique et uniforme dans une région assez petite de l'espace
et pendant un laps de temps assez court pour éviter les
effets de marées. Nous sommes donc amenés à poser
le
"principe d'équivalence faible"
(PEF):
Pour tout événement de l'espace-temps dans
un champ de gravitation arbitraire, nous pouvons choisir
un
référentiel
dit "référentiel
localement inertiel" tel que dans un voisinage
de l'événement
en question le mouvement libre de tous les corps (qui sont
donc aussi dans le champ de gravité) soit rectiligne
et uniforme tel qu'on puisse y appliquer les transformations
de Lorentz (cf. chapitre de Relativité
Restreinte).
Si nous mettons expérimentalement
PEF en défaut, alors nous mettons en défaut
le principe d'équivalence
lui-même... ce qui n'a jamais pu être réalisé
en laboratoire à ce
jour!
Remarque: Le concept de localité est très
important car il n'existe pas naturellement de champ de gravité uniforme.
Par exemple, sur Terre, deux corps ponctuels distants d'une
certaine
longueur lâchés d'une certaine hauteur tomberont au
sol avec une distance plus courte que la distance qui les
séparait
au moment où ils ont été lâchés.
C'est ce que nous appelons en physique les "effets
de marées": le champ gravitationnel n'est
jamais uniforme (dans la nature en tout cas...).
Donc le principe d'équivalence
(qui inclut le principe d'équivalence faible) affirme finalement
que la force de Newton:
 (50.1)
(50.1)
et celle de la gravitation
selon la forme de la loi de Newton-Poisson (cf.
chapitre d'Astronomie):
 (50.2)
(50.2)
sont équivalentes
telles que la masse inerte égale la masse pesante et l'accélération
égale la pesanteur et qu'il n'est pas possible de distinguer
les deux:
 (50.3)
(50.3)
 (50.4)
(50.4)
En quoi ce postulat permet-il de
résoudre toutes les difficultés alors ? C'est
simple ! L'idée
est la suivante:
Lorsque nous allons considérer
un corps en accélération, nous allons d'abord
toujours assimiler celle-ci à l'accélération
due à la chute dans un champ gravitationnel
(de par l'application du principe d'équivalence).
Ensuite, nous allons supposer, et devrons le vérifier
(démonstration
plus bas) en retrouvant la loi de Newton, que l'accélération
due à ce
champ gravitationnel n'est pas due au champ lui-même mais à la
géométrie
de l'espace déformé par la présence de
la masse (in extenso l'énergie)
qui crée le champ gravitationnel. Ainsi, l'objet n'est
plus en "chute
libre" mais sera vu comme glissant sur la trame spatiale
déformée pour acquérir ainsi son accélération.
Au fait, l'enjeu est double:
1. Si le calcul tensoriel permet d'exprimer
les lois de la mécanique classique et relativiste restreinte
dans n'importe quel système de coordonnées,
il est alors possible de voir comment le système de
coordonnées (la métrique) agit sur l'expression
des lois de l'Univers (Albert Einstein ne le savait pas tant
qu'il
n'avait pas terminé ses calculs mais le pressentait)!
2. Si l'expression tensorielle naturelle
des lois de la mécanique fait apparaître le glissement (in extenso
l'accélération) sur la trame spatiale suivant la métrique (locale)
considérée, alors le pari est gagné et alors l'accélération peut
être vue comme un effet dont la cause est purement géométrique.
Ainsi, l'extension de la
relativité
restreinte ne se fait plus en prenant en compte seulement les
systèmes
non inertiels mais la géométrie du système!!
Nous pouvons (et arrivons!) ainsi (à) contourner le
problème
initial et le pire... c'est que cela marche!!!!
 Exemple: Exemple:
Supposons que deux fusées,
que nous nommerons A et B, se trouvent dans une
région
de l'espace éloignée de toute masse. Leurs moteurs
sont arrêtés
ce qui se traduit physiquement par un mouvement rectiligne
uniforme.
Dans chaque fusée, des physiciens réalisent des expériences
de mécanique
avec des objets dont ils connaissent la masse inerte. Soudain,
le moteur de la fusée A démarre
et lui communique une accélération dont l'effet
ressenti
à l'intérieur du vaisseau spatial est une force d'inertie
qui plaque les objets vers le plancher. Pour les physiciens de
la fusée A les
lois de la mécanique sont alors les mêmes
que celles que l'on observe dans un champ gravitationnel. Ils
sont donc logiquement
amenés à interpréter la force d'inertie comme
la manifestation d'un
champ gravitationnel. À l'aide d'une balance, ils peuvent alors
peser leurs objets et leur attribuer une masse gravitationnelle.
Supposons que les physiciens
de la fusée B puissent observer ce qui se
passe dans la fusée
A. Ils savent que ce que leurs collègues interprètent
comme le poids des objets n'est en fait qu'une force d'inertie.
La force
d'inertie étant proportionnelle à l'accélération
et à la
masse inerte. Si la masse gravitationnelle était différente
de la masse inerte les physiciens de la fusée A pourraient
distinguer les effets des forces d'inertie de ceux d'un
champ de gravitation car les masses mesurées seraient
distinctes. Or, nous savons que la masse inerte et la masse
gravitationnelle
sont équivalentes (principe d'équivalence Galiléen).
Il s'ensuit que les physiciens de la fusée A n'ont
aucun moyen de faire la différence entre des forces d'inertie
résultant d'un mouvement accéléré de
leur vaisseau spatial et les forces d'attraction gravitationnelles.
Il
faut toutefois tempérer les conclusions de cette expérience:
les vrais champs de gravitation se distinguent d'un référentiel
accéléré dans la mesure où l'accélération
gravitationnelle varie avec la distance qui sépare
les corps alors que dans un référentiel
accéléré, l'accélération
est identique en tout point de l'espace.
Cependant, localement, un champ gravitationnel et un référentiel
accéléré ne peuvent être différenciés.
Nous sommes amenés maintenant
à énoncer le "principe
d'équivalence
d'Einstein" (PEE) tel que l'a fait Einstein:
localement, toutes les lois de la physique sont les mêmes
dans un champ gravitationnel et dans un référentiel
uniformément accéléré.
Ceci a une conséquence:
Si la masse (qui est équivalente à de l'énergie
comme nous l'avons vu en relativité restreinte) d'un
objet n'est pas différenciable
que nous soyons dans un champ
gravitationnel
ou dans un référentiel uniformément
accéléré c'est que tous les types d'énergie
(énergie de cohésion
nucléaire, énergie électrostatique, énergie
gravifique propre de l'objet, etc.) de cet objet ne sont
pas différenciables. Donc
les lois de la relativité restreinte sont elles aussi
valables quel que soit le référentiel considéré!
Si les lois ne sont pas
les mêmes, alors PEE est mis en défaut, donc
in extenso PEF aussi et plus généralement le
principe d'équivalence dans sa généralité
mais ceci n'est encore jamais arrivé expérimentalement.
Remarque: De par le PEF, il est intéressant
de constater que le champ gravitationnel agit aussi sur l'énergie
potentielle gravitationnelle des autres corps. Nous disons
alors que le champ
gravitationnel est un "champ couplé".
Étant donné qu'en
relativité générale, le champ gravitationnel
est censé être décrit par la métrique
 (dont
est munie la variété différentiable à 4
dimensions que constitue l'espace-temps), nous pouvons voir
un référentiel
localement inertiel comme un système de coordonnées
de l'espace-temps dans lequel la métrique (dont
est munie la variété différentiable à 4
dimensions que constitue l'espace-temps), nous pouvons voir
un référentiel
localement inertiel comme un système de coordonnées
de l'espace-temps dans lequel la métrique  devient plate (pseudo-Riemannienne):
devient plate (pseudo-Riemannienne):
 (50.5)
(50.5)
Un tel système de coordonnées existe toujours, ce
qui traduit l'existence, pour tout champ gravitationnel, de référentiels
localement inertiels!
Lorsque la métrique n'est cependant pas plate, les
coordonnées
sont appelées "coordonnées
normales de Riemann" et la métrique décrit
alors un espace Riemannien (espace courbe) et dépend
elle-même de manière non triviale
des coordonnées du système.
PRINCIPE
DE MACH
Si le principe d'équivalence met en
évidence l'égalité des masses inerte et gravitationnelle,
il ne nous éclaire pas sur la nature de ces deux masses.
Finalement, que sont les masses inerte et gravitationnelle?
La nature profonde de la masse inerte devrait nous renseigner
sur celle de l'inertie elle-même. L'inertie se manifeste sous
une forme passive - le principe d'inertie - et une forme active
- la seconde loi de Newton. D'une manière générale,
elle exprime un comportement universel des corps à résister
au changement du mouvement. Or nous savons que le mouvement
inertiel est relatif,
c'est-à-dire qu'il
n'existe aucun référentiel absolu. En est-il
de même du mouvement
accéléré? Considérons, pour
illustrer cette interrogation, une fusée dans laquelle
se trouve un physicien et réalisons deux
expériences:
- Première expérience. La fusée accélère:
le physicien est soumis à une force d'inertie orientée
dans la direction opposée à celle de l'accélération.
- Deuxième expérience. Maintenant supposons
que l'on imprime à l'ensemble de l'Univers - à l'exception
de la fusée qui se déplace selon un mouvement
inertiel - une accélération
exactement opposée à celle de la fusée lors
de l'expérience précédente.
Si le mouvement accéléré est relatif
alors, pour un observateur, il n'est pas possible de distinguer
les deux expériences. Notamment, le physicien situé à l'intérieur
de la fusée doit observer l'apparition d'une force
d'inertie
absolument identique à celle qu'il a notée
lors de la première
expérience.
La masse inerte trouverait alors son origine dans les interactions
de la masse gravitationnelle des corps avec l'ensemble des
masses gravitationnelles de l'Univers! Tout
se passe comme si en déplaçant toutes les masses
de l'Univers, celles-ci entraînaient avec elles les objets
se trouvant dans la fusée, donc le physicien ressent
alors une force qui le tire dans le même sens que l'accélération
appliquée aux étoiles.
Selon Ernst
Mach, un physicien et philosophe du 19ème siècle,
le mouvement quel qu'il soit, inertiel
ou accéléré, serait relatif. Cette théorie fut baptisée
par Einstein "principe de Mach".
Jusqu'à ce jour, le principe de Mach n'a pas été confirmé,
mais pas davantage infirmé. Il est vrai que sa vérification
expérimentale
dépasse de beaucoup les capacités humaines!
MÉTRIQUES
Einstein supposa donc que la gravitation
n'était que la manifestation de déformations
de l'espace-temps. Pour tenter d'illustrer de façon simpliste
mais très imagée l'idée
d'Einstein, considérons une roue dentée roulant à vitesse
constante (disons une dent à la seconde) sur une crémaillère.
Imaginons que nous ayons le pouvoir de modifier simultanément
le pas de la crémaillère
et celui de la roue quand et où nous le désirons. Faisons
alors en sorte que le pas de la crémaillère augmente
légèrement d'une
dent à l'autre. Pour des observateurs fixes la roue est alors
animée
d'un mouvement uniformément accéléré car,
en effet, à chaque tour
celle-ci parcourt une distance toujours plus grande. En revanche,
si l'on choisit la crémaillère comme référentiel
et le pas de celle-ci comme étalon de mesure, le mouvement
de la roue est alors uniforme (une dent par seconde). L'accélération
de la roue est la conséquence
de l'augmentation du pas de la crémaillère.
Poursuivons
l'analogie: le pas de la crémaillère joue
le rôle d'étalon
de mesure local dans notre espace à une dimension
que constitue la crémaillère.
En géométrie, il porte le nom de "métrique".
La métrique est ce qui permet de déterminer
la distance entre deux points, elle représente en quelque
sorte l'étalon infinitésimal
d'un
espace. En géométrie euclidienne la métrique
est une constante, ce qui nous permet de créer des étalons
de mesure universels. Bernhard Riemann, inventa une géométrie
où la métrique peut varier d'un
point
à un autre de l'espace, ce qui lui permit de décrire
des espaces courbes comme la surface d'une sphère par exemple
(cf.
chapitre de Géométries Non-Euclidiennes).
Lors de notre étude du calcul
tensoriel, des géométries
non-euclidiennes et de la géométrie
différentielle (chapitres dont la lecture est plus
que recommandée!!!), nous avons vu que la mesure de
la distance ds entre
deux points positionnés dans un espace à deux
ou trois dimensions peut s'effectuer au moyen d'un grand nombre
de
système de coordonnées
par "l'équation métrique"
(cf.
chapitre de Calcul Tensoriel):
 (50.6)
(50.6)
En relativité générale,
l'idée est de rendre
le modèle théorique indépendant du fond
et donc le construire sous une forme covariante (ce que certains
assimilent à un postulat sous le nom de "principe
de covariance").
Un excellent candidat pour ce type de démarche
est donc d'utiliser le formalisme tensoriel. Raison pour laquelle
l'équation de métrique en constitue aussi un
des piliers.
 Exemples: Exemples:
E1. Les coordonnées
rectangulaires (dans  ): ):
 (50.7)
(50.7)
Si la distance au carré satisfait
à cette relation alors nous sommes dans un espace plat (cf.
chapitre de Géométries Non-Euclidiennes).
E2. Les coordonnées polaires
(dans  ): ):
 (50.8)
(50.8)
d'où:

(50.9)
d'où:
 (50.10)
(50.10)
Si la distance au carré satisfait à
cette relation alors nous sommes dans un espace plat (cf.
chapitre de Géométries Non-Euclidiennes).
E3. Les coordonnées cylindriques (dans
 ) pour
lesquelles nous avons: ) pour
lesquelles nous avons:
 (50.11)
(50.11)
à remplacer dans  nous obtenons de façon quasiment identique à précédemment: nous obtenons de façon quasiment identique à précédemment:
 (50.12)
(50.12)
Si la distance au carré satisfait à cette relation
alors nous sommes dans un espace courbe (de type cylindrique)
mais qui localement peut être plat (cf.
chapitre de Géométries Non-Euclidiennes).
En réalité, pour avoir la métrique de
la surface du cylindre et non pas simplement du plan
exprimé en coordonnées cylindriques, il
faudra prendre la métrique suivante:
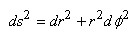 (50.13)
(50.13)
dont l'origine a été démontrée
dans le chapitre de Géométrie Différentielle.
E4. Les coordonnées sphériques
(dans
 )
pour lesquelles nous avons: )
pour lesquelles nous avons:
 (50.14)
(50.14)
à remplacer dans  nous obtenons: nous obtenons:
 (50.15)
(50.15)
Petit
rappel préalable:
 (50.16)
(50.16)
Donc:
 (50.17)
(50.17)
Après
une première série de mise en commun et de simplifications élémentaires
des termes identiques, nous obtenons:
 (50.18)
(50.18)
Si la distance au carré satisfait à cette relation
alors nous sommes dans un espace courbe (de type sphérique)
mais qui localement peut être plat (cf.
chapitre de Géométries Non-Euclidiennes).
En réalité, pour avoir la métrique de la surface de la sphère
et non pas simplement du plan exprimé en coordonnées sphériques,
il faudra prendre la métrique suivante:
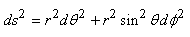 (50.19)
(50.19)
dont l'origine a été démontrée
dans le chapitre de Géométrie
Différentielle. Nous avions par ailleurs vérifié dans
le chapitre de Calcul Tensoriel, que la courbure de Ricci
de la métrique
sphérique antéprécédente était
nulle. Par contre, nous avions tout de suite après vérifié
que si nous prenions la métrique
précédente
de la surface de la sphère, la courbure de Ricci était
non nulle (et c'est encore heureux!).
Jusque-là, vous vous demandez peut-être où nous voulons
en venir. Au fait, nous cherchons à définir à partir
de ces relations, un être mathématique
qui en concordance avec l'hypothèse d'Einstein, exprime
les propriétés
géométriques d'espaces donnés.
Comment allons-nous faire?: Nous allons
d'abord changer d'écriture tout simplement. Au lieu d'utiliser
les symboles  nous
allons écrire nous
allons écrire  .
Attention! Les chiffres en suffixes ne sont pas des puissances.
Ce sont des valeurs muettes qui sont là uniquement pour symboliser
la x-ème
coordonnée d'un repère donné. .
Attention! Les chiffres en suffixes ne sont pas des puissances.
Ce sont des valeurs muettes qui sont là uniquement pour symboliser
la x-ème
coordonnée d'un repère donné.
Écrivons maintenant à nouveau
nos équations métriques
avec cette nouvelle notation en considérant qu'il ne s'agit
que d'exemples particuliers qui n'ont pas nécessairement
un sens physique pertinent (nous l'avons par ailleurs mentionné
précédemment!):
- Coordonnées rectangulaires:
 (50.20)
(50.20)
- Coordonnées polaires:
 (50.21)
(50.21)
- Coordonnées cylindriques:
 (50.22)
(50.22)
- Coordonnées sphériques:
 (50.23)
(50.23)
Maintenant rappelons
encore une fois que le "tenseur
métrique" (nommé ainsi car il étalonne l'espace-temps)
noté:
 (50.24)
(50.24)
intervient
dans l'équation métrique de la manière suivante:  (50.25)
(50.25)
et remarquez que les composantes de la
matrice sont sans dimensions aussi.
Cet être mathématique qui
est un tenseur contient donc les paramètres de la
courbure (nous disons parfois aussi de la "contrainte" ou
de la "tension") dans
lequel un espace se trouve. Mais alors que contient le tenseur
métrique
d'espace-temps pour un espace euclidien plat?
Selon la convention d'écriture
de sommation d'Einstein (cf. chapitre de
Calcul Tensoriel) par exemple,
pour  nous
avons: nous
avons:
 (50.26)
(50.26)
Donc si nous revenons à notre
tenseur pour l'espace euclidien plat, nous savons déjà (cf.
chapitre de Calcul Tensoriel) que m et n vont
de 1 à 3 et
que nous avons dans notre tenseur  pour pour
 et et
 pour pour
 (tenseur symétrique). Donc:
(tenseur symétrique). Donc:
 (50.27)
(50.27)
Ainsi:
 (50.28)
(50.28)
où comme d'habitude sur ce site nous faisons l'abus
de notation (déjà mentioné dans le chapitre
de Calcul Tensoriel) de ne pas mettre  entre
crochets (puisqu'un tenseur et sa forme matricielle sont normalement
deux choses distinctes en toute rigueur). entre
crochets (puisqu'un tenseur et sa forme matricielle sont normalement
deux choses distinctes en toute rigueur).
Ce résultat est remarquable, car le
tenseur métrique va donc nous permettre de définir
les propriétés
d'un espace à partir d'un simple être mathématique
facilement manipulable formellement.
En coordonnées polaires le tenseur
 s'écrit: s'écrit:
 (50.29)
(50.29)
Vérification:
 (50.30)
(50.30)
En coordonnées cylindriques le
tenseur  s'écrit: s'écrit:
 (50.31)
(50.31)
La vérification
ne se fait même plus tellement le résultat est évident.
En coordonnées sphériques le tenseur
 est
un peu plus complexe et s'écrit: est
un peu plus complexe et s'écrit:
 (50.32)
(50.32)
La vérification ne se fait même plus tellement le résultat
est
évident.
En
relativité restreinte, nous avons vu que les notions d'espace
et de temps
étaient implicitement liées. Ainsi, pour étudier la physique (cela
intéresse peu le mathématicien), nous avons besoin d'ajouter à notre
tenseur métrique la composante du temps pour obtenir ce que nous
appelons le "tenseur métrique d'espace-temps".
Pour
déterminer l'écriture de ce tenseur, nous allons nous
placer dans un premier temps dans un espace
de Minkowski où
nous avions rappelons-le (cf. chapitre de
Relativité Restreinte):
 (50.33)
(50.33)
qui est donc l'intervalle infinitésimal d'espace-temps
entre deux
événements infiniment voisins (ou considérés
comme tels à une certaine
échelle...).
Ainsi,
en posant:
 (50.34)
(50.34)
Nous
avons:
 (50.35)
(50.35)
avec la "signature":
 (50.36)
(50.36)
Remarque: Pour tous les tenseurs métriques que
nous avons déterminés avant, si nous les exprimons
dans l'espace-temps (donc en rajoutant le temps), les composantes
spatiales ont toutes
un signe négatif!
Nous verrons par la suite d'autres métriques beaucoup moins intuitives
une fois que nous aurons démontré bien plus loin l'équation d'Einstein
des champs.
CRITÈRE
DE SCHILD
Nous allons maintenant voir
que pour étudier la gravitation, la géométrie
courbe est nécessaire après quoi (il nous faudra
démontrer
l'équation des géodésiques avant!) nous montrerons
qu'elle est également suffisante. Nous verrons que la gravitation
telle qu'elle est formulée en mécanique newtonienne
est entièrement descriptible à partir d'une formulation
de courbure de l'espace-temps.
Imaginons d'abord une tour
d'une très grande hauteur h construite à la
surface de la Terre. Un homme A se trouve au pied de
la tour, et envoie un signal de pulsation  à son collègue B situé en haut de la
tour. Il se trouve, et nous allons de suite le démontrer,
que la pulsation
à son collègue B situé en haut de la
tour. Il se trouve, et nous allons de suite le démontrer,
que la pulsation  de l'onde reçue par B diffère de
de l'onde reçue par B diffère de  selon:
selon:
 (50.37)
(50.37)
D'où:
 (50.38)
(50.38)
Ce
décalage des pulsations (respectivement des fréquences)
dans un champ gravitationnel est ce que nous appelons "l'effet
Einstein", ou encore "redshift
gravitationnel".
Nous allons démontrer
cette relation à l'aide d'arguments classiques et connus
maintenant.
Un corps matériel
envoyé du sol vers le ciel doit lutter contre la force
de gravitation qui l'attire vers le bas. Il perdra donc une
certaine
quantité d'énergie, équivalant à l'énergie
potentielle gravitationnelle gagnée durant le trajet.
L'énergie
 du corps au niveau du sol est donc son énergie de masse à
laquelle s'ajoute l'énergie potentielle à la
hauteur de la tour:
du corps au niveau du sol est donc son énergie de masse à
laquelle s'ajoute l'énergie potentielle à la
hauteur de la tour:
 (50.39)
(50.39)
L'énergie de ce corps
une fois arrivé en haut de la tour est simplement son énergie
de masse:
 (50.40)
(50.40)
car il a dû dépenser
la quantité d'énergie mgh durant le trajet.
Le rapport des énergies est alors:
 (50.41)
(50.41)
Ce rapport étant indépendant
de la masse, on peut prendre la limite  afin d'avoir la relation pour le photon. Nous obtenons alors:
afin d'avoir la relation pour le photon. Nous obtenons alors:
 (50.42)
(50.42)
ce qui implique:
 (50.43)
(50.43)
Nous allons maintenant étudier
ce phénomène dans le cadre de l'espace-temps
de Minkowski. Nous verrons apparaître une contradiction,
ce qui motivera le passage vers un espace-temps courbe:
c'est l'argument
en
faveur d'une géométrie courbe qui a été
utilisé par Schild.
Considérons à
nouveau le schéma d'expérience de l'homme A
qui envoie une onde vers son ami B. Soit  le temps mis par A pour émettre exactement 1 cycle
de l'onde (cf. chapitre de Mécanique
Ondulatoire):
le temps mis par A pour émettre exactement 1 cycle
de l'onde (cf. chapitre de Mécanique
Ondulatoire):
 (50.44)
(50.44)
et  le temps mis par B pour recevoir ce cycle:
le temps mis par B pour recevoir ce cycle:
 (50.45)
(50.45)
À cause de l'effet Einstein,
nous savons que  et donc
et donc  en temps propre! Soit en fait que le temps passe plus lentement
pour quelqu'un au sol (A) que pour une autre personne
en haut d'une montagne (B)!
en temps propre! Soit en fait que le temps passe plus lentement
pour quelqu'un au sol (A) que pour une autre personne
en haut d'une montagne (B)!
Mais comme nous sommes en
géométrie plate et que le champ gravitationnel est
supposé statique, nous en déduisons que les trajectoires
d'espace-temps décrites par les signaux doivent être
parallèles. Ceci mène à la conclusion que l'intervalle
de temps propre serait  (selon la relativité restreinte).
(selon la relativité restreinte).
Si nous optons pour un espace courbe, nous pouvons préserver
la relation  ,
c'est-à-dire le fait que le temps avance plus lentement pour
A que pour B. Ceci se traduit simplement par le fait
qu'en géométrie courbe, le temps propre (!) d'un observateur
dépend de la métrique. ,
c'est-à-dire le fait que le temps avance plus lentement pour
A que pour B. Ceci se traduit simplement par le fait
qu'en géométrie courbe, le temps propre (!) d'un observateur
dépend de la métrique.
Les mêmes développements
peuvent être faits en assimilant l'expérience
précédente
à un train qui se déplace avec une accélération
constante g. L'observateur A se trouve dans
le compartiment arrière (équivalant au sol de
la Terre dans l'expérience
précédente) et envoie une onde à son
collègue
B situé à l'avant du train (à une
distance
h).
L'observateur B reçoit l'onde après un temps
 .
Durant ce laps de temps, le train a accéléré,
et sa vitesse a augmenté d'une valeur .
Durant ce laps de temps, le train a accéléré,
et sa vitesse a augmenté d'une valeur  .
Par conséquent, l'onde perçue par B sera
altérée
par l'effet Doppler conventionnel (cf. chapitre
de Mécanique Ondulatoire): .
Par conséquent, l'onde perçue par B sera
altérée
par l'effet Doppler conventionnel (cf. chapitre
de Mécanique Ondulatoire):
 (50.46)
(50.46)
Nous retrouvons le résultat
initial de l'effet Einstein en écrivant simplement:
 (50.47)
(50.47)
ce qui donne glorieusement:
 (50.48)
(50.48)
Nous retrouvons plus souvent cette relation sous la forme
ci-dessous dans la littérature en utilisant les relations
entre pulsation et fréquence et la force de gravitation
de Newton pour expliciter g
et en posant h comme valant 1:
 (50.49)
(50.49)
Nous retrouvons également cette dernière relation
sous la forme condensée suivante:
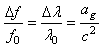 (50.50)
(50.50)
Le même résultat peut être obtenu en utilisant la
métrique de
Schwarzschild (voir plus loin), d'où le nom de cet effet qui
peut aussi être obtenu à partir des outils de la relativité générale
d'Einstein. Nous démontrerons simplement plus tard à
l'aide de cette métrique que le temps s'écoule
effectivement moins vite dans un champ gravitationnel (hypothèse
que nous avons faite quelques paragraphes plus haut).
Nous voyons dans tous les cas que  puisque
le terme de droite est positif et non nul. Cela signifie simplement
que l'onde électromagnétique en analogie au spectre des couleurs
se décale vers le rouge. Ainsi, l'effet Einstein est bien un redshift
gravitationnel. puisque
le terme de droite est positif et non nul. Cela signifie simplement
que l'onde électromagnétique en analogie au spectre des couleurs
se décale vers le rouge. Ainsi, l'effet Einstein est bien un redshift
gravitationnel.
La différence de fréquence est très faible et par conséquent difficilement
mesurable même avec les meilleurs spectroscopes. La moindre perturbation
peut totalement masquer l'effet Einstein. Il faudra véritablement
attendre 1960 pour que l'expérience de Pound et Rebka permette de
mesurer un décalage de fréquences avec une précision de 1% ne laissant
dès lors plus aucun doute quant à la réalité du phénomène.
ÉQUATIONS
DU MOUVEMENT
Nous allons démontrer ici que l'équation du
mouvement d'une particule libre est constante le long de sa
ligne d'Univers
en nous limitant d'abord au cas d'un espace plat (de type espace
de Minkowski). Après quoi, nous généraliserons
ce résultat
à tout type d'espace en utilisant un développement
simple, pour montrer de manière assez évidente
que l'équation
du mouvement est indépendante de la masse et suit
la courbure de l'espace!!! Enfin, nous présenterons
une deuxième
démonstration dans tout type d'espace en utilisant
le principe variationnel.
Commençons donc par démontrer
l'équation du mouvement d'une particule libre dans un
espace plat.
Lors de notre étude
de la relativité restreinte, nous avons démontré
le lagrangien relativiste d'une particule libre donné par
(attention! la notation m est celle de la masse au
repos
 de la particule conformément
à ce que nous avons montré dans le chapitre de Relativité
Restreinte!!!):
de la particule conformément
à ce que nous avons montré dans le chapitre de Relativité
Restreinte!!!):
 (50.51)
(50.51)
et pour cela nous étions
partis de l'action (hypothétique):
 (50.52)
(50.52)
et nous étions arrivés
à écrire:
 (50.53)
(50.53)
Maintenant, montrons quelque
chose d'intéressant. Rappelons que pour l'espace-temps
de Minkowski, nous avons obtenu:
 (50.54)
(50.54)
en nous restreignant à
une seule dimension spatiale, nous obtenons comme relation:
 (50.55)
(50.55)
et alors... eh bien voilà
au fait, si nous posons:
 (50.56)
(50.56)
nous avons finalement:
 (50.57)
(50.57)
nous retrouvons donc la même
action à partir d'une forme plus générale
(pure) de l'action qui est:
 (50.58)
(50.58)
résultat que nous avions aussi démontré dans
le chapitre d'Électrodynamique!! Nous pouvons même
faire mieux en termes d'élégance...! Si nous
observons bien les développements
des lignes précédentes, nous observons qu'au
fait la relation:
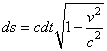 (50.59)
(50.59)
est le cas particulier à une dimension de la relation:
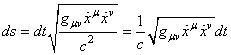 (50.60)
(50.60)
avec comme défini plus haut:
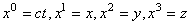 (50.61)
(50.61)
et donc:
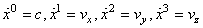 (50.62)
(50.62)
Effectivement, si nous prenons le cas à une dimension dans
un espace plat de Minkowski:
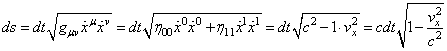 (50.63)
(50.63)
Ainsi, nous avons le facteur de Fitzgerald-Lorentz qui est
donné en toute généralité par:
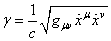 (50.64)
(50.64)
comme généralisation de la Relativité Restreinte!
Ceci étant fait, revenons à nos moutons... Dans
un espace sans champ de potentiel, nous avons démontré dans
le chapitre de
Mécanique
Analytique que le lagrangien se réduit à la simple
expression de l'énergie
cinétique tel que:
 (50.65)
(50.65)
Si nous souhaitons généraliser
cette relation pour qu'elle soit valable dans n'importe
quel type
d'espace (courbe ou plat), il nous faut introduire les coordonnées
curvilignes telles que nous les avons étudiées
en calcul tensoriel (cf. chapitre de
Calcul Tensoriel).
Dans un premier temps, cela
donne:
 (50.66)
(50.66)
où rappelons-le ds est
l'abscisse curviligne de la trajectoire.
Et nous avons démontré
en calcul tensoriel que:
 (50.67)
(50.67)
Cette dernière relation s'écrit
dans le contexte de la mécanique relativiste de manière
plus standard:
 (50.68)
(50.68)
t étant
un paramètre qui correspond en mécanique au temps
propre de la particule et qui dans la littérature spécialisée
est souvent noté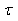 . .
Avant de nous intéresser
aux espaces courbes décrits par la métrique  (ce que nous ferons lors de notre démonstration du lagrangien
libre généralisé), restreignons-nous à
l'espace euclidien avec la métrique (ce sera un bon
exercice pour bien comprendre) donnée par la matrice
de Minkowski (cf. chapitre de Relativité Restreinte):
(ce que nous ferons lors de notre démonstration du lagrangien
libre généralisé), restreignons-nous à
l'espace euclidien avec la métrique (ce sera un bon
exercice pour bien comprendre) donnée par la matrice
de Minkowski (cf. chapitre de Relativité Restreinte):
 (50.69)
(50.69)
que nous noterons  pour la différencier des autres (car plus souvent utilisée).
Nous avons finalement dans l'espace euclidien:
pour la différencier des autres (car plus souvent utilisée).
Nous avons finalement dans l'espace euclidien:
 (50.70)
(50.70)
Maintenant, appliquons le
principe variationnel:
 (50.71)
(50.71)
La variation de ds
peut être trouvée plus simplement à partir de
la variation de  : :
 (50.72)
(50.72)
nous trouvons:
 (50.73)
(50.73)
Le facteur "2" provient du
fait que par symétrie de l'espace euclidien, les variations
de  et
et  sont égales.
sont égales.
Remarque: Comme nous le verrons après, cette relation
de

ne sera plus identique lorsque nous traiterons des espaces courbes.
En simplifiant un peu, nous
obtenons:
 (50.74)
(50.74)
Ce qui est équivalant
à écrire:
 (50.75)
(50.75)
Nous pouvons maintenant revenir
à l'action:
 (50.76)
(50.76)
Nous réécrivons l'intégrale
précédente (ce sera plus simple à traiter):
 (50.77)
(50.77)
Effectivement, vérifions
que cette forme est bien équivalente:
 (50.78)
(50.78)
Donc revenons à notre
intégrale:
 (50.79)
(50.79)
Nous avons donc deux intégrales
qu'il va être un peu plus simple d'analyser. La
première
intégrale:
 (50.80)
(50.80)
donne simplement une expression
évaluée aux extrémités temporelles  .
Dès lors, comme les valeurs de .
Dès lors, comme les valeurs de  sont parfaitement connues aux extrémités temporelles,
le variationnel
sont parfaitement connues aux extrémités temporelles,
le variationnel  est nul aux deux bornes et cette intégrale est nulle.
est nul aux deux bornes et cette intégrale est nulle.
Il ne nous reste alors plus
que l'intégrale:
 (50.81)
(50.81)
Donc pour que le principe
variationnel 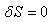 (cf.
chapitre de Mécanique
Analytique) soit respecté,
il faut que nous ayons: (cf.
chapitre de Mécanique
Analytique) soit respecté,
il faut que nous ayons:
 (50.82)
(50.82)
Or, nous pouvons réécrire
une partie de cette expression. Effectivement, nous avons:
 (50.83)
(50.83)
Rappelons par ailleurs que
nous avons démontré plus haut que:
 (50.84)
(50.84)
et que nous avons:
 (50.85)
(50.85)
Donc:
 (50.86)
(50.86)
Maintenant, rappelons que
lors de notre étude de la relativité restreinte,
nous avons démontré le cheminement qui nous amenait à
définir le quadrivecteur d'énergie impulsion:
 (50.87)
(50.87)
Donc finalement, ce qui annule
le variationnel de l'intégrale d'action peut s'écrire:
 (50.88)
(50.88)
Nous retrouvons donc l'équation
de conservation de la quantité de mouvement (conservation
de l'impulsion) que nous appelons dans le cadre de la relativité
générale "équation
du mouvement". Cette forme de l'équation
du mouvement semble dépendante de la masse mais en
fouillant un peu, nous verrons qu'il n'en est rien.
En multipliant cette relation
par  nous pouvons aussi écrire:
nous pouvons aussi écrire:
 (50.89)
(50.89)
et de même pour un
autre observateur:
 (50.90)
(50.90)
En d'autres
termes, l'impulsion de la particule reste constante sur toute
sa ligne d'Univers.
Mais nous pouvons aussi écrire:
 (50.91)
(50.91)
donc:
 (50.92)
(50.92)
Une forme plus importante
encore de l'équation du mouvement peut être obtenue.
Effectivement:
 (50.93)
(50.93)
alors:
 (50.94)
(50.94)
cette relation est donc la
forme "sans masse" de l'équation du mouvement
dans un espace euclidien ou autrement dit, dans un espace-temps
de type
Minkowski. Autrement dit, il existe donc un système de
coordonnées
en chute libre dans lequel le mouvement de la particule est
celui d'un déplacement uniforme dans l'espace-temps.
Il sera très intéressant de la comparer
avec l'équation du mouvement dans un espace courbe que
nous verrons plus loin (appelée "équation des
géodésiques").
Remarque: Il est équivalent d'écrire
les relations des équations du mouvement par rapport à l'abscisse
curviligne propre ds ou au temps propre dt (noté
traditionnellement  )
Nous pouvons maintenant montrer
que l'équation du mouvement, au même titre que l'équation
des géodésiques que nous verrons de suite après,
est invariante par transformation de Lorentz:
 (50.95)
(50.95)
Maintenant,
voyons une forme plus générale de l'équation
du mouvement pour tout type d'espace. L'objectif ici est
de mettre
en évidence, et ce en quelques lignes de calculs, que
le mouvement suivi par une particule libre est indépendant
de sa masse (vous pouvez déjà anticiper sur l'interprétation
de la trajectoire d'un photon dans un espace courbe...!).
Nous avons démontré
en calcul tensoriel (et précédemment) que:
 (50.96)
(50.96)
ce qui donne pour le lagrangien
généralisé d'une particule libre avec  (nous
retrouvons bien l'expression générale de l'énergie cinétique): (nous
retrouvons bien l'expression générale de l'énergie cinétique):
 (50.97)
(50.97)
où t est le
temps propre de la particule, c'est un invariant !
Remarque: Cette relation est appelée "lagrangien
géodésique" par certains auteurs.
Rappel: Le temps propre
est une
sorte d'horloge imaginaire qui voyage sur la particule et
quels que soient les observateurs qui regardent l'horloge,
ils seront
mathématiquement
d'accord sur la valeur de l'intervalle de temps entre deux "TIC"
de l'horloge.
Ce qui nous permet d'écrire
(attention il faut bien se rappeler des différentes
relations que nous avions déterminées lors
de notre étude du formalisme
lagrangien dans le chapitre traitant de la Mécanique
Analytique):
 (50.98)
(50.98)
Remarque: L'élimination du facteur 1/2 du Lagrangien
provient de la symétrie du tenseur métrique.
Si ce dernier n'est pas symétrique, nous pouvons toujours
le caractériser
par un tenseur qui l'est.
Effectivement,
soit  un
vecteur de coordonnées un
vecteur de coordonnées  et
soit: et
soit:
 (50.99)
(50.99)
Les  ne
sont pas symétriques a priori, mais nous pouvons écrire: ne
sont pas symétriques a priori, mais nous pouvons écrire:
 (50.100)
(50.100)
Nous posons ensuite:
 (50.101)
(50.101)
Donc:
 (50.102)
(50.102)
et les  sont
symétriques. sont
symétriques.
La forme
quadratique q peut
donc toujours s'écrire avec une matrice symétrique, il y a
même
bijection. La conclusion étant qu'un tenseur métrique
doit être symétrique si l'on veut le caractériser
par la forme quadratique qu'il définit.
L'interlude mathématique étant
terminé, continuons notre développement physique.
En conséquence
de la dernière relation, l'expression de l'hamiltonien
devient bien évidemment:
 (50.103)
(50.103)
puisque nous considérons être dans
un espace sans champ de potentiel. Le carré de la vitesse étant
dès lors constant sur toute la trajectoire, nous avons:
 (50.104)
(50.104)
Établissons maintenant les
équations du mouvement de tout corps. Nous avons:
 et
et  (50.105)
(50.105)
et comme:
 (50.106)
(50.106)
alors:
 (50.107)
(50.107)
d'où:
 (50.108)
(50.108)
en mettant en commun:
 (50.109)
(50.109)
que nous pouvons écrire identiquement
pour les  en
procédant de façon identique à ci-dessus. en
procédant de façon identique à ci-dessus.
La relation précédente donne
donc la trajectoire d'un corps en mouvement, dans un espace sans
champ de potentiel, en fonction de ses coordonnées curvilignes et
de la métrique de l'espace considéré.
Ce qui est particulièrement
intéressant dans ce résultat, c'est que la masse m
(à nouveau) s'élimine
identiquement dans cette équation du mouvement:
 (50.110)
(50.110)
Remarquez, que nous aurions
pu utiliser aussi un autre paramètre invariant que le temps
propre tel que l'abscisse curviligne ds. Dès lors
l'équation précédente s'écrirait:
 (50.111)
(50.111)
Nous pouvons encore simplifier
cette relation mais nous garderons cette simplification pour la
deuxième démonstration de l'équation du mouvement
dans un espace quelconque (en faisant usage du principe variationnel
cette fois) juste après.
Il est très (très)
intéressant d'observer que si nous restreignons la métrique
à celle d'un espace euclidien:
 (50.112)
(50.112)
avec:
 (50.113)
(50.113)
Nous obtenons alors la
simplification:
 (50.114)
(50.114)
Nous retrouvons donc la
première
équation du mouvement obtenue pour un espace plat! Le résultat
est remarquable !
Conclusion: Aux mêmes conditions
initiales de position et de vitesse curvilignes dans un espace
(plat ou courbe) sans champ de potentiel (c'est ce que nous
pourrions
penser du moins selon nos hypothèses initiales...), correspond
la même trajectoire quelle que soit la masse m
de la particule (même pour les photons - la lumière
- dont la masse est nulle!!).
Nous
pouvons maintenant étudier le principe de moindre action dans le but
de rechercher le plus court chemin (aussi bien au niveau spatial que
temporel) entre deux points dans un espace de géométrie donnée
avant de s'attaquer au cas beaucoup plus complexe du lagrangien
qui prend
en compte le tenseur des champs...
ÉQUATION
DES GÉODÉSIQUES
Intéressons-nous maintenant
à obtenir le même résultat mais en faisant usage
cette fois-ci du principe variationnel. Nous retomberons sur la
même équation que précédemment pour tout
type d'espace à la différence que cette fois-ci, nous
prendrons la peine de la simplifier pour arriver à "l'équation
des géodésiques".
En partant de (voir développements
précédents):
 (50.115)
(50.115)
avec une paramétrisation telle que
 et et
 sont
fonction d'un paramètre temporel ou spatial. sont
fonction d'un paramètre temporel ou spatial.
Pour une surface donnée sous forme
paramétrique,
nous cherchons donc à minimiser la longueur d'un arc ds en
appliquant donc le principe variationnel (non dépendant du temps
car les photons ne peuvent avoir un chemin plus rapide au sens
temporel du terme entre deux points mais uniquement un chemin plus
court - au sens métrique du terme):
 (50.116)
(50.116)
en unités naturelles. Or:
 (50.117)
(50.117)
En
développant, et comme les indices ont le même domaine de variation:
 (50.118)
(50.118)
d'où (nous avons déjà multiplié l'expression
après
la seconde égalité
par ds/ds par anticipation de l'intégrale
qui va suivre):
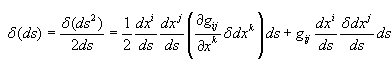 (50.119)
(50.119)
Ensuite, il nous faut donc introduire ce développement
sous l'intégrale:
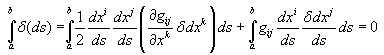 (50.120)
(50.120)
En
travaillant sur la seconde intégrale (après l'égalité),
nous posons:
 et et
 (50.121)
(50.121)
Donc par l'intégration par
partie (cf. chapitre de Calcul Différentiel
Et Intégral):
 (50.122)
(50.122)
devient:
 (50.123)
(50.123)
Soit finalement:
 (50.124)
(50.124)
Le terme non intégré ci-dessous est
négligeable à cause de la présence du facteur  : :
 (50.125)
(50.125)
Donc nous avons:
 (50.126)
(50.126)
Nous effectuons un changement d'indice:
 (50.127)
(50.127)
ce qui nous permet de factoriser
 : :
 (50.128)
(50.128)
Comme  et et
 sont
différents de zéro, c'est l'intégrande
qui doit être nulle: sont
différents de zéro, c'est l'intégrande
qui doit être nulle:
 (50.129)
(50.129)
En développant le second terme:
 (50.130)
(50.130)
Qui s'écrit encore:
 (50.131)
(50.131)
et
qui se simplifie en:
 (50.132)
(50.132)
Nous obtenons (à nouveau!!!)
le système d'équations qui définit les "géodésiques",
c'est-à-dire les droites de  .
Ces dernières constituent donc les extrémales
de l'intégrale qui
mesure la longueur d'un arc de courbe joignant deux points
donnés
dans .
Ces dernières constituent donc les extrémales
de l'intégrale qui
mesure la longueur d'un arc de courbe joignant deux points
donnés
dans  . .
Cette dernière équation,
est celle qui nous intéresse dans le cas du lagrangien
libre. Effectivement, si nous prenons le cas extrême de la
lumière (ou des photons si
vous préférez), cette dernière ne va pas
chercher le chemin le plus rapide (le plus vite) au niveau
temporel. Ce serait totalement en
contradiction avec le postulat d'invariance de voir la lumière
accélérer
en fonction du chemin!!! Dans ce contexte, cela signifie que
sur
la trame spatio-temporelle, la seule chose qui a un sens est
le plus court chemin spatial et non le plus court chemin temporel!
C'est la raison pour laquelle cette dernière équation
est appelée
"équation des géodésiques" ou
encore "équation
d'Euler-Lagrange généralisée".
Cependant, nous pouvons écrire cette
dernière équation de façon plus condensée en introduisant les symboles
de Christoffel si la métrique est un tenseur symétrique tel que
 .
Effectivement: .
Effectivement:
 (50.133)
(50.133)
et comme le symbole de Christoffel
de première espèce (cf.
chapitre de Calcul Tensoriel) est défini par:
 (50.134)
(50.134)
Remarque: Il est important de se rappeler que ce symbole contient
toute l'information sur la métrique de l'espace-temps. Nous
verrons un exemple plus bas comme quoi dans un référentiel
localement inertiel ce symbole de Christoffel est nul.
Alors l'équation d'Euler-Lagrange s'écrit:
 (50.135)
(50.135)
La multiplication contractée
(cf. chapitre de Calcul Tensoriel)
de la relation précédente
dans la base canonique par  nous donne:
nous donne:
 (50.136)
(50.136)
dans la littérature
un changement d'indice est souvent effectué afin d'avoir
au final (c'est toujours la même expression étant donné
que les indices ont le même domaine de variation!):
 (50.137)
(50.137)
avec  étant donc le symbole de Christoffel de deuxième
espèce
(cf. chapitre de Calcul Tensoriel)
donné par:
étant donc le symbole de Christoffel de deuxième
espèce
(cf. chapitre de Calcul Tensoriel)
donné par:
 (50.138)
(50.138)
et est appelé dans le cadre de la relativité générale
la "connexion
affine" ou encore "coefficients
de connexion" et qui
permet de trouver le système
de coordonnées
(via la résolution d'un système d'équations
différentielles) en
chute libre dans lequel l'équation de la particule est
celle d'un déplacement uniforme dans l'espace-temps
en fonction d'un système
de référence (les deux systèmes étant
donc reliés par la connexion
affine!).
Cette relation,
de la plus haute importance, nous permet de déterminer
comment un corps en mouvement va naturellement se déplacer
dans un espace courbe et ce peut-être... indépendamment
de sa masse !!!
Elle nous donne donc la métrique dans laquelle nous devons poser un
référentiel
pour qu'il soit inertiel par rapport au corps considéré.
L'équation des géodésiques antéprécédente
est aussi l'équation différentielle du second
ordre que doit donc satisfaire la représentation paramétrique
d'une ligne sur une surface où s
est la longueur le long de la ligne afin que sa longueur totale soit extrémale.
Selon le principe d'équivalence, nous sommes donc
en droit d'interpréter cette relation comme l'équation
du mouvement dans
un champ de gravitation
quelconque, et donc d'interpréter le deuxième terme
supplémentaire
de l'équation comme l'opposé d'un terme de force gravitationnelle
par unité de
masse, c'est-à-dire comme l'opposé d'un champ gravitationnel.
Remarque: Nous pouvons également écrire
l'équation
des géodésiques et utilisant le temps propre:
 (50.139)
(50.139)
ou encore en
utilisant la quadrivitesse:
 (50.140)
(50.140)
Encore une
fois, si nous nous restreignons à un espace-temps plat,
nous voyons trivialement que nous retombons sur la première équation
du mouvement que nous avions obtenue:
 (50.141)
(50.141)
car les composantes de la métrique de Minkowski étant constantes
les coefficients de Christoffel sont tous nuls.
Les solutions de cette dernière équation sont des lignes droites
ordinaires données par:
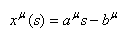 (50.142)
(50.142)
Bien évidemment, dans un espace-temps courbe général,
les géodésiques
ne pourront pas être globalement représentées
par des lignes droites. Cependant avec une approximation au
deuxième ordre en développement
de Taylor (cf. chapitre sur les Suites
Et Séries) nous arrivons à nous ramener à des
droites (ce qui revient
à ramener l'espace courbe à un espace plat).
L'important
dans tout cela, c'est que l'équation des géodésiques
permet de constater que la courbure de l'espace détermine
les trajectoires des corps qui s'y meuvent quelle que soit
leur masse, qu'ils soient
en
mouvement
uniforme ou non (observez la dérivée seconde
dans l'équation des géodésiques!). Il
ne nous reste plus alors qu'à effectuer la fin du travail
et de mettre en relation la courbure de l'espace-temps avec
l'énergie
qui s'y trouve !
LIMITE
NEWTONIENNE
Nous avons montré
plus haut (argument de Shild) que pour étudier la gravitation
(en particulier l'effet Einstein), la géométrie
courbe est nécessaire. Nous avions promis de montrer
aussi qu'elle
était suffisante. Il est temps maintenant de le faire !
Définition: La "limite
Newtonienne" est une situation physique où les
trois conditions ci-dessous sont satisfaites:
C1. Les particules se déplacent
lentement par rapport à la vitesse de la lumière.
Ce qui s'exprime comme le fait que les variations des composantes
spatiales de
leur quadrivecteur sont très inférieures à celles
de la composante temporelle (t étant le temps
propre):
 (50.143)
(50.143)
C2. Le champ de gravitation
est statique. En d'autres termes, toute dérivée temporelle
de la métrique est nulle.
C3. Le champ gravitationnel
est faible, c'est-à-dire qu'il peut être vu comme une
faible perturbation d'un espace plat:
 avec
avec  (50.144)
(50.144)
et où  est constant (seul
est constant (seul  dépend des coordonnées).
dépend des coordonnées).
Considérons l'équation
des géodésiques obtenue précédemment:
 (50.145)
(50.145)
La première condition (C1)
nous amène à la simplifier sous la forme:
 (50.146)
(50.146)
Les deux autres conditions
(C2 et C3 dont l'application a été mise en évidence dans le
développement ci-dessous) nous offrent plusieurs simplifications
dans l'expression du
symbole
de Christoffel
de deuxième
espèce:
 (50.147)
(50.147)
L'équation des géodésiques
devient alors:
 (50.148)
(50.148)
et vaut alors pour la composante temporelle
( ) : ) :
 (50.149)
(50.149)
Or (rappel de la métrique
de Minkowski)  pour
pour  et pour
et pour  nous avons (métrique statique)
nous avons (métrique statique)  .
Donc obligatoirement, nous devons conclure que .
Donc obligatoirement, nous devons conclure que  est une constante (et ce quel que soit le choix de la signature
de la métrique de Minkowski).
est une constante (et ce quel que soit le choix de la signature
de la métrique de Minkowski).
Quant aux composantes spatiales, nous savons
que  lorsque
réduit à sa partie spatiale est une simple
matrice identité lorsque
réduit à sa partie spatiale est une simple
matrice identité 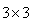 ,
ce qui donne pour chaque composante spatiale dans le cas
où nous
choisissons (par tradition uniquement!) la signature - +
+ + de la métrique de Minkowski: ,
ce qui donne pour chaque composante spatiale dans le cas
où nous
choisissons (par tradition uniquement!) la signature - +
+ + de la métrique de Minkowski:
 (50.150)
(50.150)
Bien évidemment, le lecteur peut s'amuser à faire
le
développement qui va suivre
avec la signature inverse (+ - - - ) et il verra que cela change
seulement le signe du potentiel dans le résultat final
du développement):
Notons maintenant le temps
propre  comme
il est d'usage. Nous avons alors: comme
il est d'usage. Nous avons alors:
 (50.151)
(50.151)
En divisant par  et en rétablissant
et en rétablissant  ,
nous obtenons: ,
nous obtenons:
 (50.152)
(50.152)
À partir d'ici nous posons (car nos illustres prédécesseurs
ont tâtonné avant nous):
 (50.153)
(50.153)
tel que (relation qui nous sera très utile lors de l'étude de
la métrique de Schwarzschild plus loin):
 (50.154)
(50.154)
où  est le potentiel gravitationnel, nous retrouvons l'expression
de l'accélération gravitationnelle (équation
de Newton-Poisson) de la mécanique Newtonienne (cf.
chapitre de Mécanique Classique):
est le potentiel gravitationnel, nous retrouvons l'expression
de l'accélération gravitationnelle (équation
de Newton-Poisson) de la mécanique Newtonienne (cf.
chapitre de Mécanique Classique):
 (50.155)
(50.155)
avec  . .
Ce développement,
simple mais néanmoins remarquable par son interprétation,
prouve que la géométrie courbe est suffisante
pour décrire la gravitation (et donc la théorie
de Newton)!! Cette vérification est nommée
par certains le
"principe
de correspondance".
TENSEUR D'ÉNERGIE-IMPULSION
Le tenseur d'énergie-impulsion (T.E.I.) est un outil
mathématique
utilisé (notamment) en relativité générale
afin de représenter la
répartition de masse et d'énergie dans l'espace-temps.
Prenons pour exemple le T.E.I. qui considère en relativité générale
la matière comme pouvant être approximée par un fluide parfait.
Dans le chapitre de Mécanique Des Milieux Continus nous avons démontré:
 (50.156)
(50.156)
où  a
les unités d'une force et a
les unités d'une force et  celles
d'une surface. Ainsi avec une écriture plus conventionnelle: celles
d'une surface. Ainsi avec une écriture plus conventionnelle:
 (50.157)
(50.157)
Sous forme variationnelle cela donne:
 (50.158)
(50.158)
Calculons maintenant:
 (50.159)
(50.159)
Remarque: Nous ne travaillons exprès pas avec
des éléments différentiels
afin de ne pas être coincé plus tard. C'est un peu du
bricolage
à la physicienne, mais bon cela marche (confirmé par l'expérience).
En supposant que seuls le volume et le temps font que la
force varie (ce qui suppose une densité constante quand
même et que le
système est inertiel) nous avons alors:
 (50.160)
(50.160)
Ce qui donne simplement (cf. chapitre
de Calcul Tensoriel) le
produit tensoriel des vitesses:
 (50.161)
(50.161)
Si nous généralisons cette relation aux quadrivecteurs-vitesse
de la relativité restreinte, nous avons alors par définition le "tenseur
d'énergie-impulsion":
 (50.162)
(50.162)
ou sous forme indicielle:
 (50.163)
(50.163)
soit sous forme contravariante:
 (50.164)
(50.164)
Cette relation est la justification pour laquelle
la relativité générale est aussi indiquée
comme étant une théorie des milieux continus par certains
spécialistes.
Maintenant démontrons que la dérivée:
 (50.165)
(50.165)
Remarque: Ce qui comme nous l'avons déjà signalé dans
le chapitre de Calcul Tensoriel s'écrit  dans
les vieux livres.
D'abord, rappelons que (cf. chapitre de
Relativité Restreinte):
 (50.166)
(50.166)
et admettons que nous sommes dans les faibles vitesses telles
que  .
Dès lors dans une métrique de Minkowski (+, -,
-, -): .
Dès lors dans une métrique de Minkowski (+, -,
-, -):
 (50.167)
(50.167)
Or, nous reconnaissons dans les parenthèses l'équation
de continuité (conservation
de la masse) que nous avons démontré dans le
chapitre de Thermodynamique et qui nous le savons est nulle!
Ainsi:
 (50.168)
(50.168)
Regardons par ailleurs ce que contient la composante  du
T.E.I.: du
T.E.I.:
 (50.169)
(50.169)
En termes d'unités, il s'agit d'une densité d'énergie
(nous voyons directement que cette grandeur ne peut être que
positive).
Regardons maintenant les autres composantes avec  et et
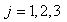 : :
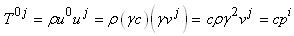 (50.170)
(50.170)
où  a les
unités d'une densité de quantité de mouvement. a les
unités d'une densité de quantité de mouvement.
Regardons maintenant les composantes du tenseur
lorsque  (nous
omettons donc la première ligne et la première colonne): (nous
omettons donc la première ligne et la première colonne):
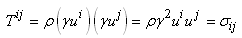 (50.171)
(50.171)
Nous retrouvons donc les composantes du tenseur des contraintes
d'un fluide parfait.
Donc finalement, le T.E.I. peut s'écrire sous la forme d'une
matrice  réelle symétrique: réelle symétrique:
 (50.172)
(50.172)
Dans le cas où les vitesses sont faibles, c'est-à-dire
 , nous avons: , nous avons:
 (50.173)
(50.173)
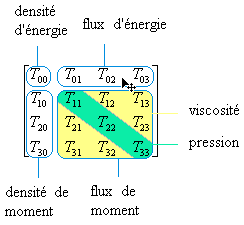
Nous retrouvons donc dans ce tenseur les interprétations suivantes
des grandeurs physiques (bien que rigoureusement toutes les composantes
aient des unités qui peuvent être vues comme densité d'énergie
soit comme une pression).
-  est
la densité volumique d'énergie (elle est positive) est
la densité volumique d'énergie (elle est positive)
-  sont
les densités de moments sont
les densités de moments
-  sont
les flux d'énergie sont
les flux d'énergie
Nous comprenons alors mieux pourquoi les anglo-saxons appellent
aussi bien cette matrice "Energie-Momentum Tensor" que "Stress-Energy-Momentum
Tensor" puisque implicitement il s'agit de modèliser l'espace
par une fluide parfait sous des contraintes de cisaillement
(forces tangentielles) et de tension (forces normales).
Remarque: La sous-matrice des composantes spatiales:
 (50.174)
(50.174)
est la matrice dite "matrice des
flux de moments" (appellation tout à fait discutable...).
En mécanique des milieux continus (cf.
chapitre de Mécanique Des Milieux Continus), nous avons
démontré que
sa diagonale correspond à la pression, et les autres composantes
aux efforts tangentiels dus à la viscosité dynamique.
Bref, pour résumer sous forme covariante:
 (50.175)
(50.175)
Montrons que la dérivée covariante (cf.
chapitre de Calcul Tensoriel) du tenseur d'énergie-impulsion
est nulle telle que:
 (50.176)
(50.176)
Donc:
 (50.177)
(50.177)
Commençons par développer le premier terme:
 (50.178)
(50.178)
Or, nous avons:
 (50.179)
(50.179)
d'où:
 (50.180)
(50.180)
Nous retrouvons entre les crochets l'équation de continuité qui
est nulle. Par contre, le premier terme entre parenthèses
est non nul comme nous l'avons vu lors de notre étude
du quadrivecteur accélération
dans le chapitre de Relativité Restreinte:
 (50.181)
(50.181)
Mais selon le principe d'équivalence faible (PEF),
nous pouvons toujours nous placer dans un référentiel
tel que localement l'accélération
soit nulle tel que (pour rappel, on ne met pas de flèches
de vecteur pour les quadrivecteurs):
 (50.182)
(50.182)
et il vient alors:
 (50.183)
(50.183)
Donc nous avons maintenant:
 (50.184)
(50.184)
Regardons ce que donne ce dernier terme mais en rappelant
d'abord que dans le chapitre de Relativité Restreinte
nous avions démontré que
la quadri-accélération s'exprimait selon:
 (50.185)
(50.185)
Soit (nous ne prenons que les deux premières composantes comme
exemples):
 (50.186)
(50.186)
Nous allons maintenant au fait montrer que:
 (50.187)
(50.187)
Commençons par montrer que  : :
 (50.188)
(50.188)
Or:
 et et  (50.189)
(50.189)
d'où:
 (50.190)
(50.190)
Maintenant montrons que  (les
autres composantes se vérifiant alors automatiquement): (les
autres composantes se vérifiant alors automatiquement):
 (50.191)
(50.191)
et donc nous avons bien:
 (50.192)
(50.192)
mais selon le PEF  alors: alors:
 (50.193)
(50.193)
et nous avons donc bien finalement:
 (50.194)
(50.194)
qui est l'expression de la conservation de l'énergie
en relativité générale! En abaissant les
indices, il vient:
 (50.195)
(50.195)
ÉQUATION D'EINSTEIN DES CHAMPS
Il est temps
maintenant de nous attaquer au plus beau, à l'une
des équations
les plus fameuses de notre époque et qui fait briller
les yeux de beaucoup de jeunes étudiants: l'équation
d'Einstein des champs. Celle qui explique pourquoi la matière
(l'énergie) courbe l'espace.
Il existe plusieurs manières de l'obtenir. Les deux plus courantes consistent
soit:
1. À avoir une approche "à l'ingénieur": C'est-à-dire que
nous procédons par comparaison avec un résultat limite connu
qui
est
la loi de gravitation de Newton (c'est celle que nous avons
choisie)
2. À avoir une approche "matheuse" (très élégante
mais un peu tombée du ciel): C'est-à-dire que
nous utilisons le formalisme lagrangien et cherchons par tatonnements
une
densité
lagrangienne
qui
nous
permet de
retomber
sur quelque chose de connu.
Bon ceci ayant été dit, rappelons avant de commencer quelques
résultats que nous avons obtenus jusqu'ici. Premièrement,
nous avons réussi à démontrer avec
brio que toute particule (supposée libre mais cela
est laissé
à l'interprétation... dans un espace courbe...)
suit l'équation du mouvement des géodésiques:
 (50.196)
(50.196)
Dans le chapitre
de Calcul Tensoriel, nous avons démontré (non sans
peine) que ce que nous appelons le "tenseur
d'Einstein" (qui est une constante dans un espace
Riemannien donné) est donné par:
 (50.197)
(50.197)
où 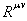 est
le tenseur de Ricci (cf. chapitre de Calcul
Tensoriel). est
le tenseur de Ricci (cf. chapitre de Calcul
Tensoriel).
Puisque la dérivée covariante du tenseur d'Einstein est nulle
et que nous avons démontré que la dérivée
covariante de T.E.I. l'est aussi, il est tentant de poser:
 (50.198)
(50.198)
où  est
un constante de normalisation et devant satisfaire la relation
pour qu'elle soit homogène au niveau des unités.
Ainsi, il vient: est
un constante de normalisation et devant satisfaire la relation
pour qu'elle soit homogène au niveau des unités.
Ainsi, il vient:
 (50.199)
(50.199)
Pour trouver l'expression de la constante, nous allons nous
placer en limite Newtonienne et exiger que la relation précédente
reproduise l'équation de Poisson pour le potentiel gravitationnel  (cf.
chapitre d'Astronomie): (cf.
chapitre d'Astronomie):
 (50.200)
(50.200)
Remarque: Cette relation montre que le potentiel de
gravitation est relié à la matière de
façon linéaire
par l'intermédiaire de ses dérivées secondes.
Einstein pensa donc que le premier membre des équations
du champ en relativité générale, membre
supposé
décrire la géométrie de l'espace-temps,
devait donc inclure d'une manière ou d'une autre les
dérivées
secondes, non pas du potentiel de gravitation, mais des potentiels
de la métrique. En fait, Einstein essaya de généraliser
le membre de droite de l'équation de Poisson: la grandeur
recherchée devait inclure non seulement la densité
de matière mais aussi l'impulsion (dès que le
corps est en mouvement, son énergie augmente et donc
sa masse). Pour évaluer l'effet gravitationnel d'un
corps il fallait donc combiner sa masse au repos avec son
impulsion. Il s'agissait
finalement du T.E.I. de rang 2 qui est la généralisation
du quadrivecteur impulsion de la relativité restreinte.
Nous avons montré plus haut que dans la limite Newtonienne
(approximation du champ faible):
 (50.201) (50.201)
et dans notre définition du T.E.I., pour
une distribution de matière au repos (ou dans un référentiel
comobile c'est selon....) seule la composante suivante est
non nulle:
 (50.202)
(50.202)
Il vient dès lors que l'équation de Poisson
peut s'écrire:
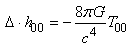 (50.203)
(50.203)
Maintenant revenons sur la relation:
 (50.204)
(50.204)
En contractant les deux membres de la relation précédente, il
vient:
 (50.205)
(50.205)
Or, le scalaire de Ricci (cf. chapitre
de Calcul Tensoriel) est
donné par  .
Il vient donc: .
Il vient donc:
 (50.206)
(50.206)
Or dans la métrique de Minkowski (avec la signature
-,+,+,+) il est immédiat
que:
 (50.207)
(50.207)
Donc:
 (50.208)
(50.208)
En utilisant cette dernière relation, l'équation:
 (50.209)
(50.209)
qui peut s'écrire aussi:
 (50.210)
(50.210)
peut finalement se mettre sous la forme:
 (50.211)
(50.211)
Intéressons-nous à la composante  telle
que la relation précédente s'écrive: telle
que la relation précédente s'écrive:
 (50.212)
(50.212)
Explicitons cette dernière relation en utilisant la définition
du tenseur de Ricci (cf.
chapitre de Calcul Tensoriel):
 (50.213)
(50.213)
Il vient alors:
 (50.214)
(50.214)
Or, le tenseur de Riemann-Christoffel sous forme développée
dans ce cas particulier est donné par (cf.
chapitre de Calcul Tensoriel):
 (50.215)
(50.215)
Remarque: En absence de champ gravitationnel et en
coordonnées
cartésiennes, il est logique que tous les symboles
de Christoffel soient nuls. En effet, les symboles de Christoffel
ne traduisent rien de plus
que
les forces d'inertie. Mais quand nous avons un champ de gravitation,
les trajectoires suivies ne sont plus des droites, même dans
le cas Newtonien alors les Christoffel sont non nuls...
À l'approximation du champ faible lentement variable
dans le temps, les symboles de Christoffel sont d'ordre O et
leurs produits sont d'ordre  et
les dérivées temporelles sont négligeables
devant les dérivées
spatiales. Il reste donc seulement les termes d'ordre O tel
que: et
les dérivées temporelles sont négligeables
devant les dérivées
spatiales. Il reste donc seulement les termes d'ordre O tel
que:
 (50.216)
(50.216)
Or, nous avons vu dans le chapitre de Calcul Tensoriel que:
 (50.217)
(50.217)
Dès lors:
 (50.218)
(50.218)
Or dans l'approximation du champ faible la variation de la métrique
par rapport au temps étant négligeable par rapport à la variation
spatiale (l'approximation est un peu tirée par les cheveux il faut
dire...):
 (50.219)
(50.219)
Par conséquent, la relation:
 (50.220)
(50.220)
devient:
 (50.221)
(50.221)
et nous constatons immédiatement qu'il s'agit de l'équation de
Poisson si et seulement si:
 (50.222)
(50.222)
constante qui est parfois appelée "constante
d'Einstein". Il s'ensuit immédiatement que
le scalaire de Ricci est positif et donc que nous sommes localement
dans
un espace à courbure de type sphérique.
L'équation d'Einstein des champs est donc sous forme définitive:
 (50.223)
(50.223)
ou de manière plus conventionnelle:
 (50.224)
(50.224)
La partie de gauche représente la courbure de l'espace-temps
telle qu'elle est déterminée par la métrique
et l'expression de droite représente une modélisation
du contenu masse/énergie de
l'espace-temps. Cette équation peut alors être interprétée
comme un ensemble d'équations décrivant comment
la courbure de l'espace-temps est reliée au contenu
masse/énergie de l'Univers. Ces équations,
ainsi que l'équation de la géodésique,
forment le coeur de la formulation mathématique de la
relativité générale.
L'équation d'Einstein est donc une équation dynamique qui décrit
comment la matière et l'énergie modifie la géométrie de l'espace-temps.
Cette courbure de la géométrie autour d'une source de matière est
alors interprétée comme le champ gravitationnel de cette source.
Le mouvement des objets dans ce champ étant décrit très précisément
par l'équation de sa géodésique.
Par ailleurs, nous venons aussi de voir que l'équation
d'Einstein se réduit aux lois de la gravité de
Newton en utilisant l'approximation des champs faibles et des
mouvements lents.
Puisque le tenseur d'énergie-impulsion comporte 16
composantes dont au fait 10 sont réellement uniques
(indépendantes) puisque
le tenseur est symétrique, nous pouvons voir l'équation
d'Einstein des champs comme dix équations différentielles
du second ordre couplées sur tenseur de champ métrique  . .
Ces équations différentielles
sont en général cauchemardesques à résoudre,
les scalaires et tenseurs de Ricci sont des contractions
du tenseur de Riemann,
qui incluent les dérivées et les produits des
symboles de Christoffel, qui eux-mêmes sont construits
sur le tenseur métrique inverse
et sur les dérivées de celui-ci. Pour corser
le tout, il est possible de construire des tenseurs d'énergie-impulsion
qui peuvent invoquer la métrique aussi. Il est donc
très
difficile de résoudre
les équations d'Einstein des champs dans le cas général
et nous devons donc souvent nous appuyer sur des hypothèses
simplificatrices.
SOLUTION DE SCHWARZSCHILD
La "métrique de Schwarzschild" (1916)
est une solution approximative de l'équation d'Einstein
dans le cas d'un champ gravitationnel isotrope et à grande
distance de la source. Elle fournit les
trois
preuves principales
de la Relativité Générale: le décalage
des horloges, la déviation
de la lumière par le Soleil et l'avance du périhélie
de Mercure. Ces trois preuves sont très importantes
car l'équation d'Einstein
n'était pas démontrée expérimentalement à l'époque.
Pour introduire cette métrique imaginons une source (par exemple
le Soleil) qui produit un champ de gravitation à l'aide de sa masse M.
Nous cherchons, pour comparer par rapport à l'expérience, les solutions
de l'équation d'Einstein (en d'autres termes: la métrique)
en dehors de la source (du Soleil donc...) de masse M.
Remarque: Il existe plusieurs techniques mathématiques
pour introduire la métrique de Schwarzschild. Le lecteur intéressé
pourra chercher par exemple dans la littérature our sur Internet
celle utilisant une transformation de jauge ("jauge d'Einstein"
avec la "jauge harmonique") pour la contrainte de perturbation
locale. Cette deuxième méthode est très élégante mais plutôt
"matheuse" et nous préférons la méthode "à l'ingénieur"...
En d'autres termes, cela revient à avoir dans la région
de l'espace qui nous intéresse (en considérant
qu'il n'y a que l'astre en question et rien d'autre autour,
n'y même l'énergie/masse propre au champ
gravitationnel) la propriété suivante:
 (50.225)
(50.225)
Donc l'équation d'Einstein des champs démontrée juste
plus haut:
 (50.226)
(50.226)
devient alors:
 (50.227)
(50.227)
Mais nous avions montré plus haut que cette dernière
relation peut aussi s'écrire à l'aide de la définition
du scalaire de Ricci  : :
 (50.228)
(50.228)
et comme la paratnèse n'est pas nulle puisque nous avons démontré
plus haut que  ,
il reste: ,
il reste:
 (50.229)
(50.229)
et donc in extenso le scalaire de Ricci est nul aussi.
Nous devons donc trouver la métrique qui satisfait
cette relation (en d'autres termes, une métrique qui
loin de la source correspond à un espace plat puisque
le tenseur de Ricci est nul). Comme il y en a plusieurs
intéressons-nous à un
cas particulièrement élégant
avec comme les aiment les physiciens... plein de symétries.
L'idée est donc de trouver une métrique si
possible indépendante
du temps (donc le champ gravitationnel aussi) et... à symétrie
sphérique
(l'astre étant lui-même de cette forme), prenant en
compte la masse de l'astre central (c'est l'objectif majeur!)
et telle qu'assez
loin de la source (...) ou lorsque la masse est nulle
nous retrouvions la métrique classique connue vue plus
haut:
 (50.230)
(50.230)
Mais ceci n'est pas totalement exact! Effectivement, nous
travaillons dans l'espace-temps. Or, nous avons vu que l'équation de la métrique curviligne
est donné dans un espace-temps plat
par:
 (50.231)
(50.231)
en passant en coordonnées sphériques nous avons alors:
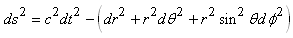 (50.232)
(50.232)
Et c'est sur cette équation de la métrique
que nous devons retomber lorsque nous sommes éloignés
de la source ou que la masse de celle-ci est extrêmement faible
(la métrique de Schwarzschild doit donc être asymptotiquement
plate, c'est-à-dire correspondre alors à l'espace plat de Minkowski).
Donc mettons-nous à la tâche. D'abord, nous partons
de ce que nous savons (vaut mieux!). C'est-à-dire que:
 (50.233)
(50.233)
et en coordonnées sphériques avec le temps
nous avons pour composantes  .
En toute rigueur, nous notons: .
En toute rigueur, nous notons:
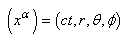 (50.234)
(50.234)
les "coordonnées de Schwarzschild".
Sur un total de 16 termes qu'implique la relation antprécédent,
nous en retenons finalement 10 à savoir
les 4 termes de la diagonale et 6 autres termes d'interaction
de sorte d'obtenir:
 (50.235)
(50.235)
où A, B, C, ...sont des coefficients à déterminer.
Avant de s'attaquer à ce travail, nous savons que selon
une de nos contraintes de départ, lorsque la masse est
faible ou que nous sommes éloignés de la source,
nous devons donc retomber sur:
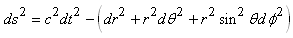 (50.236) (50.236)
dès lors intuitivement nous pouvons déjà écrire:
 (50.237)
(50.237)
ce qui admettons-le... est un net progrès...!
Si comme nous nous le sommes imposés au début,
l'équation de la
métrique est indépendante du temps, nous pouvons
par symétrie du
temps (hypothèse...) faire le changement de variable
suivant:
 (50.238) (50.238)
sans
que cela ne change quoi que ce soit dans notre  .
Or, nous nous rendons tout de suite compte que cela ne sera
pas le cas. Immédiatement, pour que cela soit satisfait
il faut: .
Or, nous nous rendons tout de suite compte que cela ne sera
pas le cas. Immédiatement, pour que cela soit satisfait
il faut:
 (50.239)
(50.239)
ce qui nous amène (c'est déjà mieux!) à:
 (50.240)
(50.240)
Maintenant si le système est bien sphérique,
l'équation de la
métrique doit être invariante par la transformation  (le
contraire se saurait depuis longtemps si ce n'était
pas le cas expérimentalement) et/ou également
pour la transformation (le
contraire se saurait depuis longtemps si ce n'était
pas le cas expérimentalement) et/ou également
pour la transformation  . .
Donc pour que cela soit juste, nous voyons immédiatement que
dans la relation précédente, nous devons imposer:
 (50.241)
(50.241)
Donc finalement nous n'avons plus que:
 (50.242)
(50.242)
où A, B, C, D seront bien évidemment indépendants
du temps (le contraire contredirait notre contrainte initiale)
mais peuvent
par symétrie de la sphère être dépendants
de r tel que:
 (50.243)
(50.243)
Maintenant, imaginons-nous sur la sphère (rigoureusement c'est
une hypersphère mais cela aide quand même...) à une
distance r fixe
du centre de la source du champ à un instant donné t fixé.
Nous n'avons alors plus que:
 (50.244)
(50.244)
puisque dt est nul (temps fixé) et dr aussi
(distance r fixée).
Nous avons par ailleurs enlevé
le signe - car nous avons anticipé le fait qu'il va s'éliminer
à la troisième égalité qui va suivre et nous le remettrons ensuite.
Maintenant, imaginons-nous proche du pôle nord de la sphère  nous
n'avons alors plus qu'en première approximation: nous
n'avons alors plus qu'en première approximation:
 (50.245)
(50.245)
et à l'équateur  : :
 (50.246)
(50.246)
Par symétrie du champ, un déplacement angulaire
infinitésimal
en chacune de ces deux zones particulières doit pourtant être égal.
Dès lors, nous ne pouvons que poser:
 (50.247)
(50.247)
Dès lors, l'équation de la métrique se réduit à:
 (50.248)
(50.248)
Montrons maintenant que nous pouvons choisir un système de coordonnées
pour lequel  . .
Introduisons pour cela une distance définie par:
 (50.249)
(50.249)
d'où:
 (50.250)
(50.250)
Il vient dès lors:
 (50.251)
(50.251)
d'où:
 (50.252)
(50.252)
Ce qui se simplifie encore en:
 (50.253)
(50.253)
Mettons le tout au carré et divisons à gauche et à droite par  : :
 (50.254)
(50.254)
d'où:
 (50.255)
(50.255)
Dès lors, l'équation de la métrique s'écrit:
 (50.256)
(50.256)
C'est donc comme si  : :
 (50.257)
(50.257)
Donc:
 (50.258)
(50.258)
Soit:
 (50.259)
(50.259)
et le tenseur métrique contravariant correspondant (dont nous
allons avoir besoin plus loin):
 (50.260)
(50.260)
tel que pour rappel (cf. chapitre de
Calcul Tensoriel):
 (50.261)
(50.261)
Maintenant, pour déterminer les coefficients restants
(soit A et B)
nous allons nous aider de la relation que doit satisfaire la
métrique si elle est effectivement localement de type
Minkowski (plate):
 (50.262)
(50.262)
et dès lors la première identité de
Bianchi (cf.
chapitre de Calcul Tensoriel) sera
automatiquement satisfaite.
Soit sous forme développée (cf. chapitre
de Calcul Tensoriel):
 (50.263)
(50.263)
avec bien évidemment (cf. chapitre de Calcul
Tensoriel):
 (50.264)
(50.264)
C'est dire que l'on a du travail sur la planche... Bon d'abord
puisque la métrique est simple les seules dérivées non nulles sont:
 (50.265)
(50.265)
Nous en déduisons simplement les 9 éléments
non nuls de la connexion (les détails sont donnés
suite à la
demande d'un lecteur):
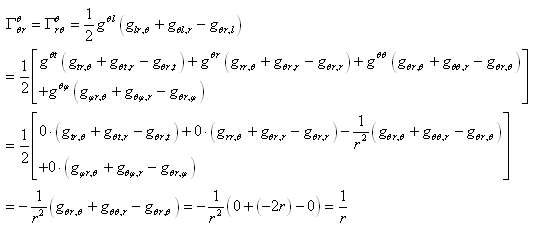 (50.266)
(50.266)
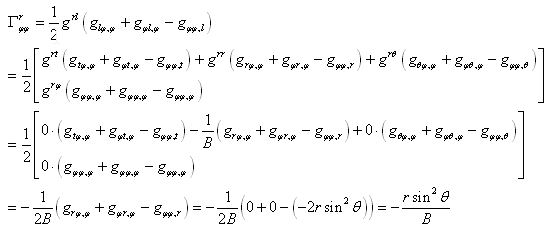 (50.267)
(50.267)
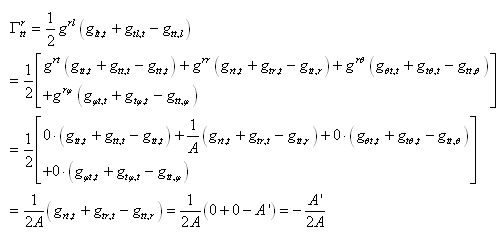 (50.268)
(50.268)
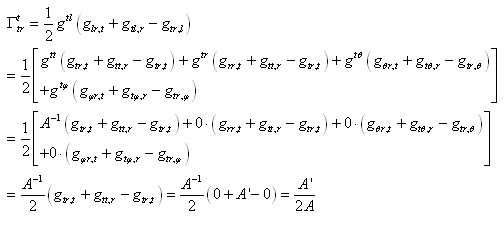 (50.269)
(50.269)
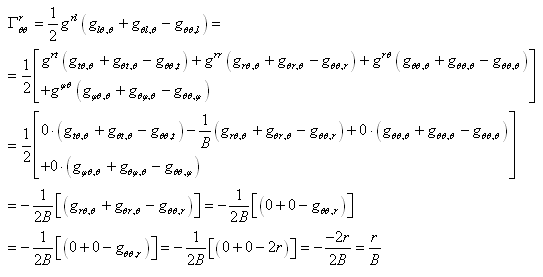 (50.270)
(50.270)
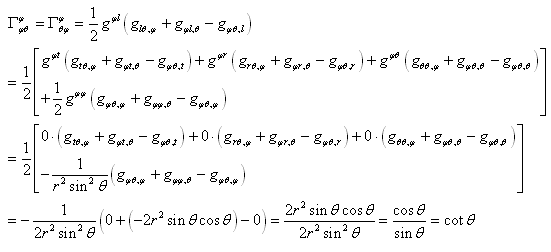 (50.271)
(50.271)
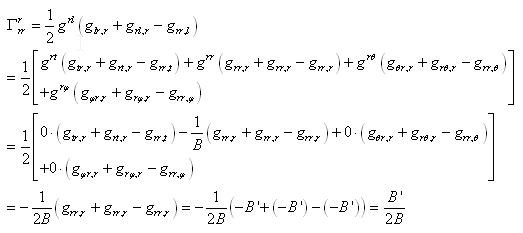 (50.272)
(50.272)
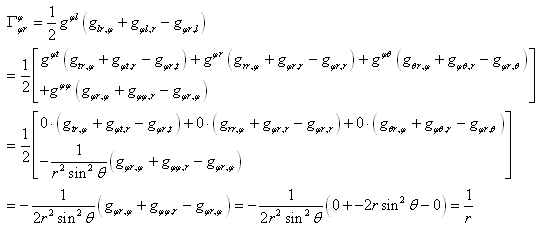 (50.273)
(50.273)
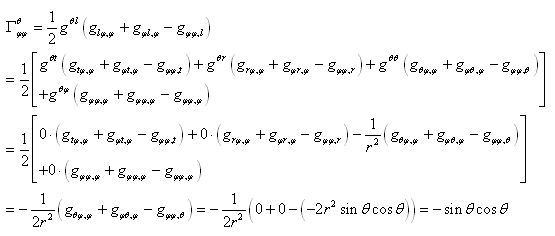 (50.274)
(50.274)
Soit pour résumer (nous avons repris
les résultats avec la signature -, +, +, + de la métrique
au lieu de +, -, -, - pour être conforme à la
tradition mais cela ne change rien au résultat final):
 (50.275)
(50.275)
Maintenant que nous avons ces termes de la connexion, il
nous faut calculer leur dérivée pour pouvoir
exprimer les deux premiers termes de:
 (50.276)
(50.276)
Il y a alors 10 termes non nuls qui sont:
 (50.277)
(50.277)
Nous avons finalement pour chaque composante du tenseur de Ricci:

(50.278)
Les seuls éléments directement non nuls sont
alors:
 (50.279)
(50.279)
Sous une forme plus conventionnelle (conforme à la
littérature)
nous pouvons simplifier un peu et par ailleurs ne garder que
les trois premières équations:
 (50.280)
(50.280)
Si nous additionnons les deux premières équations,
il nous reste:
 (50.281)
(50.281)
ce qui équivaut à:
 (50.282)
(50.282)
et cela nous donne aussi:
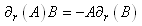 (50.283)
(50.283)
Nous avons donc:
 (50.284)
(50.284)
qui devient:
 (50.285)
(50.285)
où nous avons divisant par 2A lors du passage
de la deuxième à la troisième ligne.
Le lecteur pourra vérifier qu'une solution de l'équation
différentielle
est:
 (50.286)
(50.286)
où S est une constante réelle non nulle. En
conséquence,
la métrique pour une solution statique, symétriquement
sphérique
et dans le vide (...), s'écrit:
 (50.287)
(50.287)
Il nous reste à déterminer un coefficient. Mais comme:
 (50.288)
(50.288)
il vient:
 (50.289)
(50.289)
soit:
 (50.290)
(50.290)
Donc finalement:
 (50.291)
(50.291)
Notons que l'espace-temps représenté par cette
métrique est asymptotiquement
plat, ou, en d'autres termes lorsque  ,
la métrique s'approche de celle de Minkowski, et la
variété de
l'espace-temps ressemble à celle de l'espace de Minkowski. ,
la métrique s'approche de celle de Minkowski, et la
variété de
l'espace-temps ressemble à celle de l'espace de Minkowski.
Pour calculer les constantes K et S, nous utilisons
l'approximation du champ faible. En d'autres termes, nous nous
plaçons loin du centre, là où le champ de gravitation est faible.
Dans ce cas, la composante  de
la métrique peut être calculée. de
la métrique peut être calculée.
Effectivement, nous avions étudié plus haut
la limite newtonienne et avions obtenu la relation suivante:
 (50.292)
(50.292)
avec (cf. chapitre d'Astronomie)  .
Donc in extenso nous pouvons poser sans trop de crainte: .
Donc in extenso nous pouvons poser sans trop de crainte:
 (50.293)
(50.293)
soit:
 et et  (50.294)
(50.294)
Finalement nous avons pour la "métrique de Schwarzschild":
 (50.295)
(50.295)
soit en unités naturelles:
 (50.296)
(50.296)
Ce qui donne donc au final le tenseur métrique de Schwarzschild:
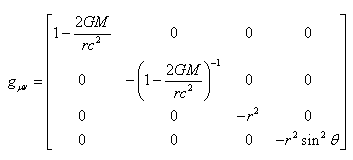 (50.297)
(50.297)
Attention!!! Certains ouvrages de référence ont la métrique
de Schwarzschild avec des signes différents car ils
prennent la métrique
-,+,+,+ au lieu de la métrique +,-,-,-.
Une singularité toute (physiquement) apparente apparaît
lorsque:
 (50.298)
(50.298)
ou en d'autres termes, lorsque la coordonnée du rayon r vaut:
 (50.299)
(50.299)
Ce rayon, que nous avions déjà déterminé lors de notre étude
la mécanique classique, est appelé "rayon
de Schwarzschild".
Le rayon de Schwarzschild est défini comme le rayon critique
prévu par la géométrie de Schwarzschild, en
deçà duquel rien ne peut s'échapper: si une étoile
ou tout autre objet atteint un rayon égal ou inférieur à son
rayon de Schwarzschild (qui dépend de sa masse, cf. ci-dessous),
alors elle devient un Trou Noir, et tout objet s'approchant à une
distance de celui-ci inférieure au rayon de Schwarzschild
ne pourra s'en échapper. Le terme est utilisé en
physique et en astronomie pour donner un ordre de grandeur de la
taille caractéristique à laquelle des effets de relativité générale
deviennent nécessaires pour la description d'objets d'une
masse donnée. Les seuls objets qui ne sont pas des trous
noirs et dont la taille est du même ordre que leur rayon
de Schwarzschild sont les étoiles à neutrons (ou
pulsars), ainsi, curieusement, que l'univers observable en son
entier.
Remarques:
R1. La singularité dans la métrique lorsque
l'on atteint le rayon de Schwarzschild est apparente car il
ne s'agit
que d'un effet
du système de coordonnées utilisées.
R2. Un théorème remarquable affirme que la métrique de Schwarzschild
est l'unique solution aux équations d'Einstein dans le vide possédant
la symétrie sphérique. Comme la métrique de Schwarzschild est également
statique, ceci montre qu'en fait dans le vide toute solution sphérique
est automatiquement statique. Une des conséquences intéressantes
de ce théorème est que n'importe quelle étoile pulsante qui reste
à symétrie sphérique ne peut pas générer d'ondes gravitationnelles
(puisque la région de l'espace-temps extérieure à l'étoile doit
rester statique).
R3. Comme les développements précédents se basent sur l'hypothèse
d'outils mathématiques (identité de Bianchi) qui nécessite
un tenseur de torsion nul, il existe des modèles plus complets
qui ne peuvent par extension pas utiliser l'équation d'Einstein
des champs.
Maintenant que nous avons la métrique de Schwarzschild revenons
sur le critère de Schild que nous avions vu lors de notre étude
classique de l'effet Einstein.
Si nous réécrivons la métrique de Schwarzschild
pour un corps immobile, nous avons la métrique qui
se simplifie en:
 (50.300)
(50.300)
En faisant intervenir le potentiel gravitationnel (cf.
chapitre d'Astronomie):
 (50.301)
(50.301)
la métrique s'écrit:
 (50.302)
(50.302)
d'où en introduisant le temps propre:
 (50.303)
(50.303)
d'où:
 (50.304)
(50.304)
soit:
 (50.305)
(50.305)
Le développement au deuxième ordre en série de Maclaurin (cf.
chapitre de Suite Et Séries) de la racine négative donne:
 (50.306)
(50.306)
Ainsi, nous avons:
 (50.307)
(50.307)
Donc cela démontre que la courbure (la gravitation)
engendre une dilatation du temps d'autant plus importante (dans
le sens
qu'il s'écoule plus vite) que le champ de gravité
est intense (la masse M est grande) ou que nous sommes
près du corps sous l'influence du champ (rayon r petit).
Or, pour la Terre, le terme:

est relativement faible. Mais pour un Trou Noir
ou une étoile à Neutrons, ce n'est plus vraiment le cas et la dilatation
devient importante et les effets accessibles à la mesure.
VÉRIFICATIONS EXPÉRIMENTALES
Nous allons maintenant passer en revue les quatre vérifications
expérimentales classiques du 20ème siècle
de la théorie de la relativité générale
qui sont:
1. La précession du périhélie qui au niveau
des résultats numériques nous posait problème
avec les outils de la mécanique classique (cf.
chapitre d'Astronomie).
2. La déflexion des ondes électromagnétiques
(lumière) passant proches d'un corps stellaire massif
qui au niveau des résultats numériques nous
posait aussi problème avec les outils de la mécanique
classique (cf. chapitre d'Astronomie).
3. La démonstration du critère de Schild (déjà
faite dans les paragraphes précédents) comme
seul moyen d'expliquer rigoureusement le redshift gravitationnel
et l'hypothèse
de ralentissement du temps dans un champ gravitationnel.
4. Le retard des signaux électromagnétiques
se propageant près du corps massif. Retard désigné sous
le nom "d'effet Shapiro" dont les applications numériques
sont utilisées pour le fonctionnement du G.P.S et que
nous verrons plus loin.
PRÉCESSION DU PÉRIHÉLIE DE MERCURE
Traitons donc maintenant un des plus fameux exemples de la
relativité
générale: la précession du périhélie
de Mercure. Nous avions déjà
traité ce cas dans le chapitre d'Astronomie,
mais nous avions mentionné
que le résultat théorique numérique ne
correspondait pas à l'expérience.
Nous allons voir en l'équivalent d'une dizaine de pages
A4 de développements
détaillés comment la relativité générale
permet de réconcilier
théorie
et expérience.
Pour étudier ce cas, nous allons utiliser le formalisme
lagrangien vu dans le chapitre de Mécanique Analytique.
D'abord, rappelons que nous avons obtenu pour la métrique de Schwarzschild:
 (50.308)
(50.308)
Ce que nous noterons en divisant par  : :
 (50.309)
(50.309)
et pour abréger les notations, nous posons  tel
que: tel
que:
 (50.310)
(50.310)
Maintenant rappelons que (cf. chapitre
de Mécanique Analytique) en unités naturelles:
 (50.311)
(50.311)
Donc (c'est très grossier mais cela fonctionne... c'est aussi ça
parfois la physique...):
 (50.312)
(50.312)
Enfin cela signifie que le lagrangien est:
 (50.313)
(50.313)
Les équations de Lagrange nous donnent pour la coordonnée  : :
 (50.314)
(50.314)
avec donc:
 (50.315)
(50.315)
d'où:
 (50.316)
(50.316)
et:
 (50.317)
(50.317)
d'où finalement pour la coordonnée  : :
 (50.318)
(50.318)
Faisons de même pour  .
Nous avons d'abord: .
Nous avons d'abord:
 (50.319)
(50.319)
et:
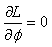 (50.320)
(50.320)
et il vient immédiatement de par l'application de l'équation
d'Euler-Lagrange:
 (50.321)
(50.321)
Faisons de même pour t:
 (50.322)
(50.322)
et il vient ici aussi immédiatement:
 (50.323)
(50.323)
Dès lors:
 (50.324)
(50.324)
Maintenant nous allons supposer que le mouvement de Mercure
est dans le plan équatorial tel que  .
Dès lors, la relation obtenue plus haut: .
Dès lors, la relation obtenue plus haut:
 (50.325)
(50.325)
se simplifie en:
 (50.326)
(50.326)
d'où:
 (50.327)
(50.327)
Nous avons aussi dès lors l'expression de la ligne
d'Univers qui pour rappel est:
 (50.328)
(50.328)
qui puisque  (qui
est donc une constante) se
simplifie en: (qui
est donc une constante) se
simplifie en:
 (50.329)
(50.329)
Faisons mainentenant le remplacement suivant:
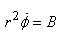 (50.330)
(50.330)
qui est donc une constante comme nous l'avons
démontré juste plus haut ainsi que le remplacement
suivant (qui est aussi une constante comme nous l'avons démontré juste
plus haut):
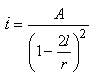 (50.331)
(50.331)
dans
l'élément de ligne d'Univers et nous obtenons::
 (50.332)
(50.332)
Considérons aussi r comme fonction  alors: alors:
 (50.333)
(50.333)
d'où:
 (50.334)
(50.334)
Ainsi, nous pouvons réécrire la ligne d'Univers
sous la forme:
 (50.335)
(50.335)
Faisons un changement de variable en posant:
 (50.336)
(50.336)
d'où:
 (50.337)
(50.337)
Ce qui donne pour notre ligne d'Univers:
 (50.338)
(50.338)
ou:
 (50.339)
(50.339)
en différenciant:
 (50.340)
(50.340)
ou écrit autrement:
 (50.341)
(50.341)
ce qui se simplifie et se factorise en:
 (50.342)
(50.342)
La première solution possible est bien évidemment:
 (50.343)
(50.343)
d'où comme r=1/u:
 (50.344)
(50.344)
Le mouvement circulaire est donc aussi une solution du problème
de Kepler en relativité générale dans un champ de Schwarzschild.
L'autre solution sera:
 (50.345)
(50.345)
Soit écrit autrement:
 (50.346)
(50.346)
elle correspond à l'orbite du problème de Kepler.
Faisons la comparaison en considérant en mécanique de Newton
le mouvement d'une particule de masse m dans un potentiel U.
Le lagrangien (cf. chapitre de Mécanique
Analytique)
est alors:
 (50.347)
(50.347)
En coordonnées polaires nous avons déjà vu
dans différents chapitres
(de Calcul Vectoriel et d'Astronomie) que la vitesse s'écrit
alors:
 (50.348)
(50.348)
En utilisant l'équation d'Euler-Lagrange nous avons l'équation
du mouvement:
 (50.349)
(50.349)
ce qui donne:
 et et
 (50.350)
(50.350)
d'où:
 (50.351)
(50.351)
et comme nous l'avons vu dans le chapitre d'Astronomie:
 (50.352)
(50.352)
est la constante des aires. Introduisons:
 (50.353)
(50.353)
d'où:
 (50.354)
(50.354)
et donc:
 (50.355)
(50.355)
Ainsi:
 (50.356)
(50.356)
L'équation:
 (50.357)
(50.357)
devient alors:
 (50.358)
(50.358)
Or:
 (50.359)
(50.359)
d'où:
 (50.360)
(50.360)
soit:
 (50.361)
(50.361)
ou:
 (50.362)
(50.362)
Il s'agit donc de la "formule
de Binet non relativiste" qui donne donc la relation
entre u=1/r et  pour
une force centrale (cf. chapitre d'Astronomie). Dans le cas
d'un potentiel newtonien: pour
une force centrale (cf. chapitre d'Astronomie). Dans le cas
d'un potentiel newtonien:
 (50.363)
(50.363)
d'où:
 (50.364)
(50.364)
avec pour rappel:
 (50.365)
(50.365)
Or, rappelons la forme de celle que nous avions obtenue avec la
relativité générale:
 (50.366)
(50.366)
Ainsi, nous voyons que le terme analogue en relativité est:
 (50.367)
(50.367)
et que la relativité générale ajoute
le terme  .
Or, comme en relativité générale: .
Or, comme en relativité générale:
 (50.368)
(50.368)
Alors:
 (50.369)
(50.369)
Or, dans le cas de l'approximation des champs faibles:
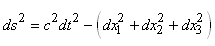 (50.370)
(50.370)
d'où:
 (50.371)
(50.371)
donc finalement:
 (50.372)
(50.372)
Ceci dit, il est vraiment intéressant de remarquer que l'équation
pour la relativité générale:
 (50.373)
(50.373)
peut être interprétée comme l'équation de Binet pour la mécanique
classique:
 (50.374)
(50.374)
avec le potentiel:
 (50.375)
(50.375)
avec  . .
Revenons maintenant à notre équation:
 (50.376)
(50.376)
Nous aimerions savoir si le deuxième terme à droite
de l'égalité
est négligeable ou non par rapport au premier terme
de droite de l'égalité et ce afin de pouvoir
appliquer la théorie des perturbations.
Nous allons d'abord poser à l'aide de l'approximation des champs
faibles faite plus haut:
 (50.377)
(50.377)
Maintenant calculons le rapport:
 (50.378)
(50.378)
Rappelons qu'en coordonnées polaires:
 (50.379)
(50.379)
en approximation, nous pouvons grossièrement poser
que:
 (50.380)
(50.380)
Dès lors pour Mercure...:
 (50.381)
(50.381)
Donc nous voyons de suite que nous pourrons appliquer les
théories
variationnelles sur le terme  .
Ainsi, posons: .
Ainsi, posons:
 (50.382)
(50.382)
L'équation:
 (50.383)
(50.383)
prend alors la forme:
 (50.384)
(50.384)
Pour résoudre cette équation différentielle,
nous allons utiliser l'approche de la théorie des perturbations
(cf.
chapitre de Calcul Différentiel Et Intégral).
Nous allons donc nous intéresser à une solution
de la forme d'un développement de Taylor en deuxième
ordre seulement en  : :
 (50.385)
(50.385)
où  sont
bien évidemment dépendants de sont
bien évidemment dépendants de  et
devront être déterminés! Pour cela, nous savons qu'il faut remplacer
l'expression précédente dans l'équation différentielle telle que: et
devront être déterminés! Pour cela, nous savons qu'il faut remplacer
l'expression précédente dans l'équation différentielle telle que:
 (50.386)
(50.386)
Ce qui se simplifie en:
 (50.387)
(50.387)
où rappelons que:
 (50.388)
(50.388)
est l'équation classique obtenue plus haut:
 (50.389)
(50.389)
considérons la solution du type:
 (50.390)
(50.390)
où D est une constante arbitraire. Or, comme nous l'avons
vu dans le chapitre d'Astronomie dans le cas de la précession
du périhélie:
 (50.391)
(50.391)
est au fait une ellipse. Ce qui signifie que toute solution de
la forme:
 (50.392)
(50.392)
est aussi une ellipse!
Pour l'équation en  : :
 (50.393)
(50.393)
qui se simplifie en:
 (50.394)
(50.394)
Puisque (cf. chapitre de Trigonométrie):
 (50.395)
(50.395)
Il vient:
 (50.396)
(50.396)
Pour déterminer  ,
décomposons-le en
trois termes: ,
décomposons-le en
trois termes:
 (50.397)
(50.397)
Ce qui nous donne immédiatement (en injectant les trois
termes respectivement dans la dérivée seconde et le terme seul):
 (50.398)
(50.398)
Donc finalement:
 (50.399)
(50.399)
La solution cherchée est finalement:
 (50.400)
(50.400)
C'est donc avec:
 (50.401)
(50.401)
qu'il faut calculer le déplacement du périhélie (on y arrive...).
Nous voyons relativement vite en observant la relation précédente
que le seul terme dont l'amplitude n'est pas constante est  . .
Rappelons alors que (cf. chapitre de Trigonométrie):
 (50.402)
(50.402)
Ce qui peut grossièrement s'écrire aussi en
première approximation en utilisant les développement
de Maclaurin au premier ordre (cf. chapitre
de Suites Et Séries):
 (50.403)
(50.403)
d'où:
 (50.404)
(50.404)
Nous savons que l'orbite d'ordre zéro est:
 (50.405)
(50.405)
L'effet du dernier terme:
 (50.406)
(50.406)
est donc d'introduire une petite variation périodique dans la
distance radiale. Ce terme n'affecte pas le déplacement du périhélie.
C'est le terme  dans: dans:
 (50.407)
(50.407)
qui introduit une non-périodicité qui peut être non négligeable
dans le cas où  est
grand. est
grand.
Le périhélie (point le plus proche du Soleil) se présente donc
quand r est minimum soit  maximum.
Or, u est maximum quand le terme qui nous intéresse est maximum,
c'est-à-dire: maximum.
Or, u est maximum quand le terme qui nous intéresse est maximum,
c'est-à-dire:
 (50.408)
(50.408)
Nous avons approximativement:
 (50.409)
(50.409)
Pour deux périhélies successifs, nous avons un intervalle:
 (50.410)
(50.410)
au lieu de  .
Ainsi, le déplacement pour une révolution est: .
Ainsi, le déplacement pour une révolution est:
 (50.411)
(50.411)
où K est donc la constante des aires et M la masse
de l'astre central et puisque:
 (50.412)
(50.412)
Bref, nous avons au final:
 (50.413)
(50.413)
Relation à comparer avec celle que nous avons obtenue dans
le chapitre d'Astronomie avec un traitement newtonien classique:  (50.414)
(50.414)
Nous retrouvons donc à la perfection le facteur 6
qui manquait dans les traitements classiques!
Pour Mercure une application numérique donne:  (50.415)
(50.415)
et l'expérience donne  .
De l'aveu même d'Einstein, en obtenant ce résultat il eut des
palpitations et l'impression de frôler la crise cardiaque et
satisfait de son effort herculéen qui l'avait totalement épuisé
il prit une longue période de repos. .
De l'aveu même d'Einstein, en obtenant ce résultat il eut des
palpitations et l'impression de frôler la crise cardiaque et
satisfait de son effort herculéen qui l'avait totalement épuisé
il prit une longue période de repos.
Pour terminer sur ce sujet, signalons une deuxième écriture
fréquente dans la littérature concernant le résultat
obtenu. Effectivement, nous avons démontré dans le chapitre
d'Astronomie que le paramètre focal était donné par:
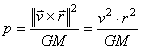 (50.416)
(50.416)
Il reste donc:
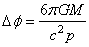 (50.417)
(50.417)
et nous avons démontré aussi dans le chapitre de Géométrique
Analytique que:
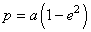 (50.418)
(50.418)
Il vient donc au final la forme la plus classique:
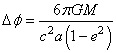 (50.419)
(50.419)
DÉFLÉXION DE LA LUMIÈRE
Nous avons donc montré que:
 (50.420)
(50.420)
en remplaçant les facteurs par leurs valeurs respectives,
nous avons:
 (50.421)
(50.421)
Mais nous avons vu plus haut que:
 (50.422)
(50.422)
et comme K est la constante des aires donnée par la conservation
du moment cinétique lui-même constant (cf.
chapitre de Mécanique Classique):
 (50.423)
(50.423)
Nous avons alors pour un photon  . .
Finalement l'équation du mouvement d'un photon se résume à:
 (50.424)
(50.424)
Posons maintenant pour simplifier les notations:
 (50.425)
(50.425)
alors:
 (50.426)
(50.426)
Le terme à droite de l'égalité est petit (vu les constantes qui
y interviennent...) si bien qu'une forme approchée de l'équation différentielle
est:
 (50.427)
(50.427)
Dont une solution particulière, qui nous le savons
d'avance, est intéressante:
 (50.428)
(50.428)
Nous portons cette solution approximée dans l'équation différentielle
initiale et nous obtenons:
 (50.429)
(50.429)
Soit:
 (50.430)
(50.430)
Soit:
 (50.431)
(50.431)
La suite va être très subtile (comment deviner quelque chose comme
cela...?). D'abord nous allons créer une nouvelle équation différentielle:
 (50.432)
(50.432)
L'astuce consiste à multiplier cette équation par i et
la sommer à l'équation différentielle d'origine:
 (50.433)
(50.433)
Ce que nous noterons:
 (50.434)
(50.434)
L'astuce est de chercher une solution particulière de la relation
précédente sous la forme:
 (50.435)
(50.435)
Nous avons alors:
 (50.436)
(50.436)
Ceci injecté dans notre nouvelle équation différentielle donne:
 (50.437)
(50.437)
Nous en déduisons immédiatement:
 (50.438)
(50.438)
Une solution particulière de l'équation différentielle d'origine
est donc:
 (50.439)
(50.439)
Soit en utilisant les relations trigonométriques remarquables:
 (50.440)
(50.440)
Il vient:
 (50.441)
(50.441)
La solution générale est finalement:
 (50.442)
(50.442)
Si nous admettons que la lumière est très faiblement déviée par
le Soleil, le rayon de courbure (1/r) de sa trajectoire sera
très faible.
Ainsi:
 (50.443)
(50.443)
tel que:
 (50.444)
(50.444)
Le premier terme est prédominant par rapport au deuxième à cause
du facteur  qui
est très petit sur le deuxième. Pour la suite, nous procédons
comme dans le chapitre d'Astronomie (juste les notations
changent) pour
l'étude de l'angle de déflexion (si vous n'y revenez pas
vous ne pourrez comprendre la justification de ce qui va être
fait!). Nous posons sans perdre en généralité que: qui
est très petit sur le deuxième. Pour la suite, nous procédons
comme dans le chapitre d'Astronomie (juste les notations
changent) pour
l'étude de l'angle de déflexion (si vous n'y revenez pas
vous ne pourrez comprendre la justification de ce qui va être
fait!). Nous posons sans perdre en généralité que:
 (50.445)
(50.445)
Soit:
 (50.446)
(50.446)
et comme:
 (50.447)
(50.447)
il vient:
 (50.448)
(50.448)
En utilisant les relations trigonométriques à nouveau:
 (50.449)
(50.449)
Il vient:
 (50.450)
(50.450)
 étant
supposé très petit nous faisons un développement de Maclaurin
(cf. chapitre de Suites Et Séries)
au premier ordre des fonctions trigonométriques: étant
supposé très petit nous faisons un développement de Maclaurin
(cf. chapitre de Suites Et Séries)
au premier ordre des fonctions trigonométriques:
 (50.451)
(50.451)
Ce qui donne:
 (50.452)
(50.452)
Donc après une série d'approximations... et
d'hypothèses limites
acceptables..., nous arrivons à:
 (50.453)
(50.453)
au lieu du résultat que nous avions obtenu selon l'approche newtonienne
dans le chapitre d'Astronomie:
 (50.454)
(50.454)
Nous trouvons donc le facteur 2 qui faisait défaut
au traitement classique du problème, relativement aux
mesures expérimentales,
que nous avons vues dans le chapitre d'Astronomie.
 (50.455)
(50.455)
Ce qui est souvent représenté de façon imagé
dans les médias par le dessin suivant:

Cette déviation a pu être mise
en évidence en mesurant la position des étoiles
au voisinage du disque solaire lors de l'éclipse
de 1919 par Arthur Eddington et son équipe.
Après
l'avance du périhélie de Mercure,
il s'agissait du second test passé avec succès
par la Relativité Générale.
C'est cet événement
qui a rendu Albert Einstein célèbre auprès
du grand public. Aujourd'hui, la déviation
des rayons lumineux a pu être mesurée avec
beaucoup plus de précision en considérant les
signaux radio émis par des sources extragalactiques
(quasars, AGN, etc.): la prédiction de la Relativité Générale
a été confirmée au millième près.
La déviation des rayons lumineux est
aujourd'hui très importante en cosmologie observationnelle,
puisqu'elle est à l'origine du phénomène
de mirage gravitationnel, encore appelée "lentille
gravitationnelle".
Il est intéressant de remarquer que toute
la théorie des mirages gravitationnels est basée
sur la relation:
 (50.456)
(50.456)
du moins pour un détecteur ponctuel.
C'est le seul ingrédient de Relativité Générale
utilisé dans
le calcul des images.
EFFET SHAPIRO
En 1964, Shapiro démontra qu'un rayon lumineux n'était
pas seulement dévié en passant près d'une
masse, mais également que la durée de
son trajet était allongée par rapport à une
géométrie euclidienne.
Il calcula que le retard devait atteindre environ 200 microsecondes,
donc parfaitement mesurable, pour une ligne de visée
rasant le Soleil. Il suggéra alors de mesurer systématiquement
la durée mise par un
signal radar pour effectuer le trajet aller-retour entre la
Terre et une planète passant derrière le Soleil
(pour que l'effet soit maximal). Cela fut d'abord accompli
avec des échos radar sur Mars,
Vénus ou Mercure, avec une précision de l'ordre
de 20%. Le résultat
est très net: la durée nécessaire à un
signal radar pour faire l'aller-retour Terre-Planète
augmente brutalement juste avant que la planète passe
derrière le Soleil et diminue tout aussi brutalement
quand celle-ci réapparaît.
Remarque: Nous parlons parfois de "ralentissement de la
lumière"
près du Soleil pour décrire l'effet Shapiro
mais c'est une expression maladroite et erronée. Comme
cela a déjà été mentionné, la
vitesse de la lumière est constante en relativité générale
aussi bien qu'en relativité restreinte. Dans le cas
de l'effet Shapiro (et dans d'autres cas similaires), ce qui
change c'est l'écoulement
du temps là où
passe la lumière, par rapport à ce qu'il est là où se
situe l'observateur.
Bien qu'il s'agisse d'un effet faible, on a pu le vérifier très
précisément depuis l'arrivée des sondes Viking sur Mars en 1976,
à l'aide de signaux envoyés depuis la Terre vers Mars et réfléchis
sur cette dernière par les sondes (voir le principe de l'expérience
sur la figure suivante). En outre, il existe même désormais un
objet de plus en plus courant pour le fonctionnement duquel
l'effet Shapiro
doit être pris en compte: le "G.P.S." (Global Positioning
System). En effet, malgré la faiblesse du champ de gravitation
terrestre, une précision géographique de quelques mètres nécessite
de tels détails dans les calculs. Toutefois, un satellite a été lancé récemment
dont le but est de vérifier, dans le champ de gravitation terrestre,
un effet encore plus faible prédit par la relativité générale
et qui n'intervient même pas dans le GPS: l'entraînement de
l'espace-temps, aussi nommé "effet
Lense-Thirring".
Signalons pour le GPS que deux phénomènes d'erreur sont connus
dans le cadre de la relativité:
1. Les satellites tournant autour de la Terre à une
vitesse approximative de 20'000 kilomètres par heure
retardent alors de 7 millionièmes
de seconde par jour (relativité restreinte).
2. À l'altitude de 20'200 kilomètres, celle
de l'orbite des satellites, le champ gravitationnel plus faible
fait avancer les horloges satellitaires
de 45 millionièmes de seconde par jour.
La somme des deux corrections donne une dérive de 38 millionièmes
de seconde par jour, un chiffre ahurissant pour un système GPS
dont la précision se doit d'être de 50 milliardièmes de seconde
par jour.
Faisons le calcul pour un rayon frôlant la surface du Soleil.
Pour cela, nous reprenons notre métrique de Schwarzschild:
 (50.457)
(50.457)
avec:
 (50.458)
(50.458)
Pour un photon, nous savons que  et
donc l'équation de la métrique de Schwarzschild s'écrit alors: et
donc l'équation de la métrique de Schwarzschild s'écrit alors:
 (50.459)
(50.459)
La trajectoire du photon ayant lieu dans le plan équatorial du
Soleil, nous posons:
 (50.460)
(50.460)
ce qui simplifie encore l'équation de la métrique en:
 (50.461)
(50.461)
Pour simplifier encore plus nous faisons l'hypothèse
que la trajectoire (en coordonnées polaires)
du photon rasant le Soleil est rectiligne telle que (pour
une des composantes polaires
du plan):
 (50.462)
(50.462)
où 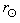 est
le rayon du Soleil. Nous allons utiliser cette hypothèse
pour simplifier l'équation de la métrique.
Pour cela nous réarrangeons: est
le rayon du Soleil. Nous allons utiliser cette hypothèse
pour simplifier l'équation de la métrique.
Pour cela nous réarrangeons:
  (50.463)
(50.463)
Nous dérivons (cf. chapitre de Calcul Différentiel
Et Intégral):
 (50.464)
(50.464)
Si nous mettons le tout au carré:
 (50.465)
(50.465)
d'où:
 (50.466)
(50.466)
Nous pouvons maintenant récrire l'équation de la métrique:
 (50.467)
(50.467)
En prenant la racine:
 (50.468)
(50.468)
Étant donné que  et
que et
que  alors: alors:
 (50.469)
(50.469)
Dès lors nous avons en utilisant les développements de Maclaurin
(cf. chapitre de Suites Et Séries)
au premier ordre:
 (50.470)
(50.470)
Nous avons alors:
 (50.471)
(50.471)
Nous avons finalement une fois condensé:
 (50.472)
(50.472)
Ce qu'il est de tradition de noter (nous sortons le 1/c
des différents termes):
 (50.473)
(50.473)
S'il n'y a pas de masse alors l'espace-temps est plat et  .
Dès lors: .
Dès lors:
 (50.474)
(50.474)
Nous pouvons ainsi distinguer le temps classique du temps
supplémentaire
engendré par l'espace courbe. Le "retard" sera donc donné par:
 (50.475)
(50.475)
Ensuite, pour intégrer les quatre fonctions de r il
faut se placer dans un référentiel placé si
possible au centre de l'astre principal (le Soleil typiquement)
puisque la métrique de Schwarzschild
est basée sur cette hypothèse pour rappel...
Ainsi, pour connaître
le retard d'un rayon lumineux partant du Soleil jusqu'à la
Terre, nous choisirons logiquement comme rayon de départ
celui du Soleil
lui-même
et comme rayon d'arrivée, la distance Soleil-Terre (donc
cela correspondra une fois les primitives calculées aux bornes
d'intégration).

Figure: 50.1 - Temps d'aller-retour d'un signal en fonction de la position
de Mars
Bon cela dit c'est bien joli de connaître les notations
d'usage, mais c'est encore mieux de faire une application numérique!
Nous allons donc d'abord déterminer la primitive de
chacun des termes ci-dessous:
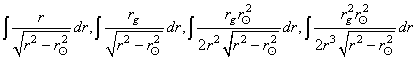 (50.476)
(50.476)
Les deux premières primitives sont simples car il s'agit
de primitives usuelles démontrées en détail
dans le chapitre de Calcul Différentiel Et Intégral:
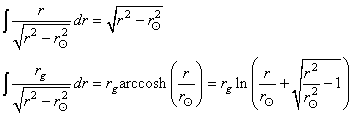 (50.477)
(50.477)
où pour la dernière primitive nous avons préservé la constante
d'intégration (contrairement à ce qui a été fait dans le chapitre
de Calcul Différentiel Et Intégral car 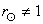 ). ).
Maintenant il nous reste les deux dernières intégrales. Commençons
dans l'ordre par:
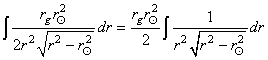 (50.478)
(50.478)
En posant:
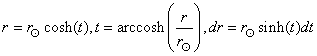 (50.479)
(50.479)
et en utilisant les résultats démontrés dans le chapitre
de Calcul Différentiel Et Intégral, nous avons alors:
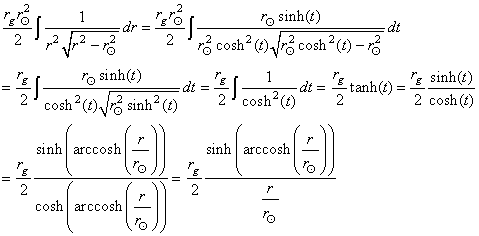 (50.480)
(50.480)
Puisque nous avons (cf. chapitre de
Trigonométrie):
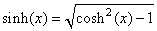 (50.481)
(50.481)
Alors:
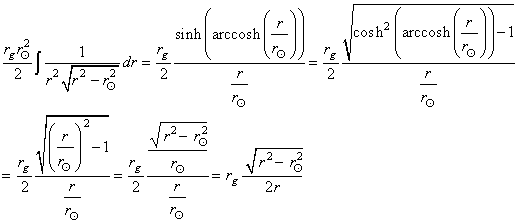 (50.482)
(50.482)
Enfin, il reste la dernière primitive:
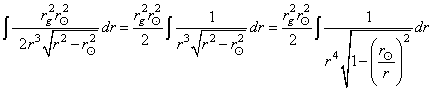 (50.483)
(50.483)
Nous posons pour la suite:
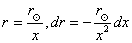 (50.484)
(50.484)
Il vient alors:
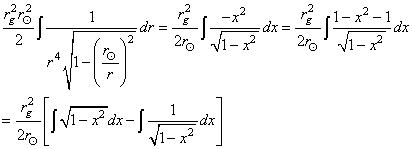 (50.485)
(50.485)
Dans le chapitre de Calcul Différentiel Et Intégral nous
avons démontré que:
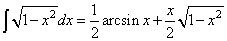 (50.486)
(50.486)
et que:
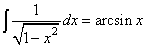 (50.487)
(50.487)
Donc:
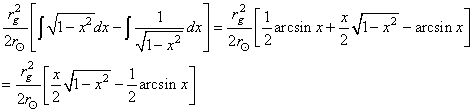 (50.488)
(50.488)
Pour revenir à l'intégrale du début on se rappelle que  .
Donc: .
Donc:
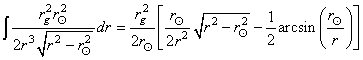 (50.489)
(50.489)
Nous avons donc au final en prenant tous les primitives calculés
plus haut en en choississant une borne de départ et d'arrivée
pour le calcul:

(50.490)
Nous voyons dans le cas limite Newtonien où  ,
cette relation se réduit comme peau de chagrin à: ,
cette relation se réduit comme peau de chagrin à:
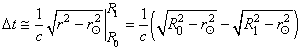 (50.491)
(50.491)
Donc pour un aller-retour (entre planète et satellite par
exemple), il vient alors dans ce cas simplifié:
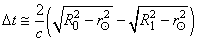 (50.492)
(50.492)
TROUS NOIRS
En restant toujours à notre métrique de Schwarzschild....Une
trajectoire radiale de type lumière implique:
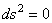 (50.493)
(50.493)
donc: 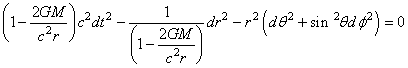 (50.494)
(50.494)
et dans une trajectoire radiale directe (par définition)
nous avons aussi:
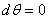 et et 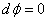 (50.495)
(50.495)
donc:
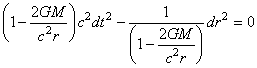 (50.496)
(50.496)
Dès lors:
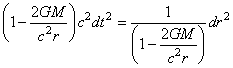 (50.497)
(50.497)
Il vient alors:
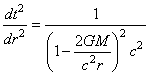 (50.498)
(50.498)
D'où:
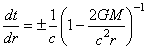 (50.499)
(50.499)
Posons en unités naturelles 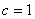 .
Il vient alors: .
Il vient alors:
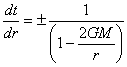 (50.500)
(50.500)
Lorsque 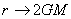 le
membre de droite de l'égalité tend vers le
membre de droite de l'égalité tend vers 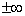 ,
donc l'évolution du temps t (observateur extérieur)
en fonction de r tend vers l'infini par rapport au temps
propre de la lumière. ,
donc l'évolution du temps t (observateur extérieur)
en fonction de r tend vers l'infini par rapport au temps
propre de la lumière.
La sphère donnée par le rayon:
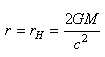 (50.501)
(50.501)
définit "l'horizon
du Trou Noir de Schwarzschild".
Vers cette frontière limite, la lumière
semble mettre un temps infini par rapport à un observateur
extérieur à se
déplacer
lorsqu'elle approche un Trou Noir. Elle ne parvient donc jamais
vraiment à l'atteindre
par rapport à l'observateur, d'où le fait que les Trous
Noirs peuvent être
entourés en fonction de leur environnement d'un halo
lumineux aux abords du rayon de Schwarzschild. De plus, puisque
le temps
semble
arrêté, la fréquence de la lumière
environnant le Trou Noir tend vers zéro et donc vers
l'infra-rouge.
Signalons encore un point très important.
Avant Einstein, la géométrie était considérée
comme partie intégrante des lois. Einstein a montré que
la géométrie de l'espace évolue dans le
temps selon d'autres lois, encore plus profondes. Il est important
de bien comprendre ce point. La géométrie de
l'espace ne fait pas partie des lois de la nature. Par conséquent,
rien que nous puissions trouver dans ces lois ne dit ce qu'est
la géométrie de l'espace. Ainsi, avant de commencer à résoudre
les équations de la théorie générale
de la relativité d'Einstein, nous n'avons strictement
aucune idée de ce qu'est la géométrie.
Nous la découvrons seulement une fois les équations
résolues.
Cela signifie que les lois de la nature doivent
s'exprimer sous une forme qui ne présuppose pas que
l'espace ait une géométrie fixe. C'est le coeur
de la leçon einsteinienne. Cette forme se traduit en
un principe appelé "indépendance
par rapport au fond". Ce principe énonce
donc que les lois de la nature peuvent être décrites
dans leur totalité sans présupposer la géométrie
de l'espace.
In extenso, le choix des quatre dimensions fait
partie du fond. Serait-il possible qu'une autre théorie
plus profonde ne nécessite pas de présupposer
le nombre de dimensions?
En résumé, l'idée de l'indépendance
par rapport au fond, dans sa formulation la plus générale
est une façon sage de faire de la physique: faite de
meilleures théories, dans lesquelles les choses qui,
avant, étaient postulées, seront expliquées
en permettant à de telles choses d'évoluer dans
le temps en fonction de lois nouvelles.
C'est là aussi une difficulté de
la théorique quantique. Elle est dépendante de
fond contrairement à la relativité générale.

- La relativité générale,
M. Ludvigsen, Éditions Dunod, ISBN10: 210004896
(241 pages) - Imprimé en 2005
 16 16  0 0 |
Commentaires:
Warning: mysql_connect() [function.mysql-connect]: [2002] Connection timed out (trying to connect via tcp://p101.arquivo.pt:3306) in /home/www/f9f6c3f0bb515fb7fa59d2c99a31acd3/web/htmlfr/php/commentaires/config/fonctions.lib.php on line 46
Warning: mysql_connect() [function.mysql-connect]: Connection timed out in /home/www/f9f6c3f0bb515fb7fa59d2c99a31acd3/web/htmlfr/php/commentaires/config/fonctions.lib.php on line 46
Warning: mysql_select_db() expects parameter 2 to be resource, boolean given in /home/www/f9f6c3f0bb515fb7fa59d2c99a31acd3/web/htmlfr/php/commentaires/config/fonctions.lib.php on line 47
Warning: mysql_query() expects parameter 2 to be resource, boolean given in /home/www/f9f6c3f0bb515fb7fa59d2c99a31acd3/web/htmlfr/php/commentaires/config/fonctions.lib.php on line 50
Warning: mysql_fetch_array() expects parameter 1 to be resource, null given in /home/www/f9f6c3f0bb515fb7fa59d2c99a31acd3/web/htmlfr/php/commentaires/config/fonctions.lib.php on line 51
[] 
Warning: mysql_close() expects parameter 1 to be resource, boolean given in /home/www/f9f6c3f0bb515fb7fa59d2c99a31acd3/web/htmlfr/php/commentaires/config/fonctions.lib.php on line 58
|
|