|

CALCUL ALGÉBRIQUE | ALGÈBRE
ENSEMBLISTE | CALCUL
DIFFÉRENTIEL ET INTÉGRAL
SUITES
ET SÉRIES | CALCUL
VECTORIEL | ALGÈBRE
LINÉAIRE | CALCUL
TENSORIEL
CALCUL
SPINORIEL
|
10.
CALCUL DIFFÉRENTIEL ET INTÉGRAL (2/2)
|
Dernière mise à jour de ce chapitre:
2017-01-31 10:12:07 | {oUUID 1.685}
Version: 3.4 Révision 6 | Avancement: ~95%
 vues
depuis le 2012-01-01:
7'523 vues
depuis le 2012-01-01:
7'523
 LISTE DES SUJETS TRAITÉS SUR CETTE PAGE
LISTE DES SUJETS TRAITÉS SUR CETTE PAGE
INTÉGRALES CURVILIGNES
Les intégrales curvilignes sont aussi très importantes
en physique. Le lecteur les retrouvera ainsi dans le chapitre de
Mécanique Classique, Magnétostatique et Électrodynamique
pour calculer le travail d'une force ou encore la "circulation
d'un champ", ou encore dans le chapitre de Géométrie
Euclidienne pour le calcul du centre de gravité de courbes
(fonctions) pesantes, ou encore dans le chapitre Formes Géométriques
pour le calculer la surface de certains corps de révolution
mais aussi en Physique Quantique Corpusculaire pour la fameuse "intégrale
de chemin" (qui n'est d'autre que le terme utilisé par les
physiciens pour dire "intégrale curviligne") ou encore pour le
calcul d'intégrales
particulières
utilisant le théorème des résidus démontré dans
le chapitre d'Analyse Complexe ou encore pour de nombreuses transformations
d'état dans le chapitre de Thermodynamique. Raison pour
laquelle il n'y aura pas ici d'exemple d'application tellement
ils sont nombreux dans les autres chapitres.
Avec la définition des ce intégrales, nous pourrons
démontrer deux résultats très importants détaillés
dans le chapitre de Calcul Vectoriel et qui sont respectivement
le théorème de Green, le théorème de
Stokes ou encore le théorème des résidus démontré dans
le chapitre d'Analyse Complexe et déjà mentionné dans
le paragraphe précédent (c'est suffisamment important
pour le mentionner deux fois!).
INTÉGRALE CURVILIGNE D'UN CHAMP SCALAIRE
Considérons une courbe C paramétrée
(cf.
chapitre de Géométrie Différentielle)
par une fonction vectorielle 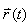 avec avec
 de
classe de
classe  par
morceaux (cette condition est nécessaire pour
que l’on puisse intégrer
sur la courbe sans problèmes). par
morceaux (cette condition est nécessaire pour
que l’on puisse intégrer
sur la courbe sans problèmes).
Définitions: D1. La courbe est dite "courbe fermée" si 
D2. La courbe est dite "courbe régulière" si 
Rappelons qu'une courbe paramétrée peut être écrite
sous la forme suivante (toute fonction vectorielle peut être écrite
sous cette forme):
 (10.1)
(10.1)
Considérons une fonction ou un "champ
scalaire" 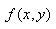 définie
dans un voisinage de C. Subdivisons définie
dans un voisinage de C. Subdivisons 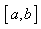 en
n sous-intervalles en
n sous-intervalles 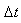 de
même
longueur tel que: de
même
longueur tel que:
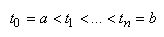 (10.2)
(10.2)
Nous choisissons sur chaque sous-intervalle un point
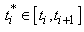 .
Soit .
Soit 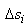 la
longueur de l'arc de C reliant les points la
longueur de l'arc de C reliant les points 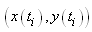 et et
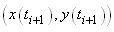 ,
l'intégrale
de f de long de C est définie comme étant "l'intégrale
curviligne" ou "intégrale
de chemin": ,
l'intégrale
de f de long de C est définie comme étant "l'intégrale
curviligne" ou "intégrale
de chemin":
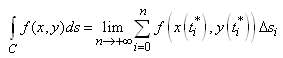 (10.3)
(10.3)
Ce qui comme nous le savons, peut s'écrire
(cf. chapitre de Géométrie Différentielle
ou Formes Géométrique
ou encore Mécanique Analytique):
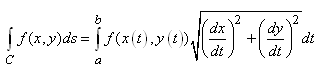 (10.4)
(10.4)
et qui peut évidemment immédiatement être étendu
au cas à 3 variables et plus.
Soit sous forme vectorielle:
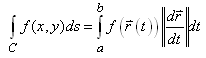 (10.5)
(10.5)
L'intégrale curviligne est linéaire,
c'est-à-dire que si 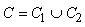 et
que et
que 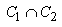 est
un point, alors (sans aller dans la définition rigoureuse
de ce qu'est l'union de deux courbes...): est
un point, alors (sans aller dans la définition rigoureuse
de ce qu'est l'union de deux courbes...):
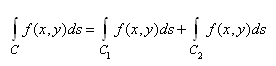 (10.6)
(10.6)
INTÉGRALE CURVILIGNE D'UN CHAMP VECTORIEL
Considérons un champ de vecteur (par exemple un champ de
force) tel que:
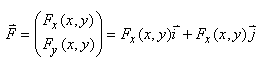 (10.7)
(10.7)
et une élément infinitésimal
d'une courbe (chemin)  morceaux
tel: morceaux
tel:
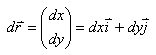 (10.8)
(10.8)
L'idée est alors de considérer que
le produit scalaire (projection de champ vectoriel sur l'élément
de chemin) représente le travail le long de l'élément
différentiel:
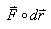 (10.9)
(10.9)
Par conséquent le travail sur tout le chemin sera donné par
(en utilisant au passage la propriété de linéarité de
l'intégrale):
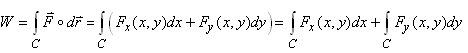 (10.10)
(10.10)
ce qui peut évidemment se généraliser à n dimensions. Indiquons que lorsque l'intégrale curviligne
(de chemin) d'un champ vectoriel est étendue à une
courbe fermée, nous parlons alors de "circulation
du champ vectoriel".
Comme:
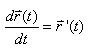 (10.11)
(10.11)
Nous avons alors une écriture assez courante:
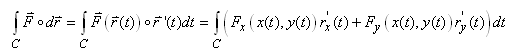 (10.12)
(10.12)
En physique souvent les problèmes sont dans le plan et nécessitent
le passage aux coordonnées polaires, ce qui en outre facilite
les calculs.
 Exemple: Exemple:
Calculons le travail de la force de pesanteur déplaçant
une masse M du point 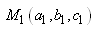 au
point au
point 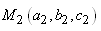 le
long d'un chemin arbitraire C. Les projections de la force de pesanteur
sur les axes de coordonnées
sont: le
long d'un chemin arbitraire C. Les projections de la force de pesanteur
sur les axes de coordonnées
sont:
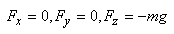 (10.13)
(10.13)
Le travail accompli est alors:
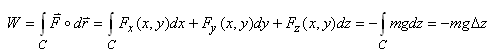 (10.14)
(10.14)
et nous retrouvons un résultat connu du chapitre
de Mécanique Classique.
Une intégrale curviligne d'un champ vectoriel
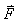 le
long d'une courbe le
long d'une courbe 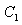 est
indépendante du chemin d'intégration
si: est
indépendante du chemin d'intégration
si:
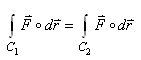 (10.15)
(10.15)
pour toute courbe 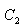 ayant
les mêmes points de
départ et d'arrivée. De plus, si le champ de vecteurs
satisfait (où G en physique est typiquement un potentiel): ayant
les mêmes points de
départ et d'arrivée. De plus, si le champ de vecteurs
satisfait (où G en physique est typiquement un potentiel):
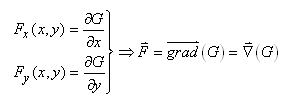 (10.16)
(10.16)
tel que (le lecteur y reconnaîtra une forme
différentielle totale exacte):
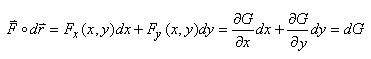 (10.17)
(10.17)
Alors l'intégrale de chemin sur une courbe
arbitraire dépend uniquement de la différence des
valeurs de la fonction G aux deux extrémités!
Démonstration:
Si la forme différentielle du champ de vecteur
satisfait bien une différentielle totale exacte, nous avons:
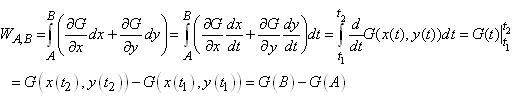 (10.18)
(10.18)
 C.Q.F.D. C.Q.F.D.
Donc l'intégrale curviligne d'une différentielle
totale exacte ne dépend pas du chemin d'intégration
mais seulement des extrémités. Nous en déduisons également
que si 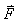 dérive
donc d'un potentiel scalaire et que A = B, l'intégrale
curviligne est alors nulle. dérive
donc d'un potentiel scalaire et que A = B, l'intégrale
curviligne est alors nulle.
En physique ce résultat s’interprète
en disant que le travail fourni par une force 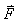 dérivant
d'un potentiel scalaire s'exerçant sur une particule élémentaire
lors d'un déplacement fini ne dépend pas du
chemin suivi. dérivant
d'un potentiel scalaire s'exerçant sur une particule élémentaire
lors d'un déplacement fini ne dépend pas du
chemin suivi.
Définitions:
D1. Lorsque la courbe C est fermée
et que l'intégrale de chemin a un résultat indépendant
du sens dans lequel ce chemin est parcourue, nous utilisons la
notation (la lettre sous l'intégrale pouvant évidemment
varier...):
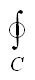 (10.19)
(10.19)
Si cette intégrale fermée est toujours
nulle, nous disons que le champ vectoriel intégré est
un "champ conservatif" et "dérive
d'un potentiel scalaire" (et donc satisfait le théorème
de Schwarz pour pouvoir être écrit sous forme de différentielle
totale exacte) puisque ceci découle de la démonstration donnée déjà
juste plus haut.
D2. Lorsque la valeur de l'intégrale de
chemin fermée dépend du sens de parcours, nous utilisons
la notation suivante (la lettre sous l'intégrale pouvant évidemment
varier...):
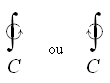 (10.20)
(10.20)
Ainsi, si le sens est direct (c'est-à-dire "anti-horlogique" ou
encore "trigonométrique") comme la notation de
gauche, son signe sera positif; si au contraire le sens est horlogique
son signe sera négatif (voir la démonstration dans
le chapitre d'Analyse Complexe). Nous parlons alors respectivement
souvent de "sens négatif" ou "sens positif".
Ainsi, pour résumer, une intégrale
curviligne (de chemin) est entièrement définie par
l'expression sous le signe de l'intégrale, la forme de la
courbe d'intégration
et le sens d'intégration.
Remarque: Le lecteur pourra trouver des démonstrations
de propriétés très importantes des intégrales
curvilignes dans le chapitre de Calcul Vectoriel comme le théorème
de Green-Riemann ou encore une étude d'application particulière
aux fonctions holomorphes dans le chapitre d'Analyse Complexe.
ÉQUATIONS DIFFÉRENTIELLES
Définition: En mathématiques,
une "équation
différentielle" (E.D.) est une relation entre
une ou plusieurs fonctions inconnues et leurs dérivées
jusqu'à l'ordre
n. "L'ordre" d'une
équation différentielle correspond au degré maximal
de différentiation
auquel une des fonctions inconnues y a été soumise.
Par rapport à notre objectif d'essayer de voir comment
la mathématiques
décrit la réalité sensible, les équations
différentielles remportent
un franc succès, mais sont également la source de
bien des soucis. D'abord des difficultés de modélisation
(voir par exemple le système
d'équation différentielles de la relativité générale...),
des difficultés
de résolution (il n'existe pas de méthode générale!),
puis des difficultés proprement mathématiques, enfin
des difficultés liées
au fait que certaines équations différentielles ne
sont pas stables par nature et donnent des solutions chaotiques
(voir le chapitre
de dynamique des populations pour des exemples simples flagrants!).
Remarque: Les équations différentielles
sont utilisées pour construire
des modèles mathématiques de phénomènes
physiques et biologiques, par exemple pour l'étude de la
radioactivité ou la mécanique céleste.
Par conséquent, les équations différentielles
représentent un immense
champ d'étude, aussi bien en mathématiques pures
qu'appliquées.
L'équation différentielle d'ordre n la plus générale peut
toujours s'écrire sous la forme:
 (10.21)
(10.21)
Nous ne considérons sur ce site que le cas où x
et y sont à valeur dans  .
Une solution à une telle E.D. sur l'intervalle .
Une solution à une telle E.D. sur l'intervalle  est
une fonction est
une fonction  (une
fonction (une
fonction  qui
est n fois continûment dérivable) telle que pour
tout qui
est n fois continûment dérivable) telle que pour
tout  ,
nous ayons: ,
nous ayons:
 (10.22)
(10.22)
Remarques:
R1. Pour des raisons qui seront développées par
la suite, nous disons aussi "intégrer l'E.D." au
lieu de "trouver
une solution à l'E.D.". La première expression se retrouve
particulièrement dans la littérature anglo-saxonne.
R2. Étant donné que tout le site Internet est bourré d'exemples
d'équations différentielles avec conditions initiales
(on parle alors de "problème de Cauchy") et de méthodes
de résolutions
dans les chapitres sur la mécanique, la physique atomique,
la cosmologie, l'économétrie, les suites et séries,
etc., nous ne ferons pas d'exemples ici et ne nous intéresserons
donc qu'à l'aspect théorique
minimal.
ÉQUATIONS DIFFÉRENTIELLES DU 1ER ORDRE
Une équation différentielle du 1er ordre est donc une E.D. qui
ne fait intervenir que la première dérivée y'.
Définition: Une équation différentielle
du 1er ordre
est dite "E.D. d'ordre 1 à variables
séparées" si elle peut s'écrire sous la forme:
 (10.23)
(10.23)
Une telle équation différentielle peut s'intégrer facilement.
En effet, nous écrivons:
 (10.24)
(10.24)
Puis symboliquement:
 (10.25)
(10.25)
Remarque: Nous écrivons ici explicitement la constante d'intégration
arbitraire  (qui
est implicitement présente dans les intégrales indéfinies) pour
ne pas l'oublier!
Il s'agit donc d'abord de trouver des primitives F et G de f et
de g, et ensuite d'exprimer y en terme de x (et
de C):
 (10.26)
(10.26)
La constante d'intégration est fixée lorsqu'on
demande que pour un  donné,
nous ayons une valeur donnée de donné,
nous ayons une valeur donnée de  .
Nous parlons alors de "problème aux valeurs initiales". .
Nous parlons alors de "problème aux valeurs initiales".
ÉQUATIONS DIFFÉRENTIELLES LINÉAIRES
Définition: Une équation différentielle d'ordre n est
dite "E.D. linéaire" (E.D.L.)
si et seulement si elle est de la forme:
 (10.27)
(10.27)
Avec:
 (10.28)
(10.28)
Voyons maintenant une propriété qui peut sembler
négligeable
au premier coup d'oeil mais qui va prendre de l'importance plus
loin!
Nous allons montrer que L est une application linéaire:
 (10.29)
(10.29)
Et pour tout  : :
 (10.30)
(10.30)
Nous disons alors que l'E.D. linéaire représente
un modèle linéaire si les multiples de cette fonction (ou toute
combinaison linéaire) sont aussi solution. Ainsi, en physique,
pour un système linéaire, l'amplification de la cause implique
une amplification de l'effet (les systèmes sont souvent linéaires
dans le cas scolaires mais dans la réalité ils sont plutôt l'exception!).
Par exemple, l'équation différentielle ordinaire
d'ordre 2 du pendule simple démontrée dans le chapitre de Mécanique
Classique n'est pas linéaire car elle contient un terme en sinus
qui n'est pas séparable.
Définition: L'équation différentielle (c'est
la plus courante en physique):
 (10.31)
(10.31)
s'appelle "équation homogène"
(E.H.) ou "équation sans second membre" (ESSM) associée à:
 (10.32)
(10.32)
Nous allons maintenant démontrer une propriété importante
des E.H.: l'ensemble  des
solutions de E.H. est le noyau de l'application linéaire L
(ce qui rappelons-le signifie: des
solutions de E.H. est le noyau de l'application linéaire L
(ce qui rappelons-le signifie:  )
et l'ensemble {S} des solutions à )
et l'ensemble {S} des solutions à  est
donné par: est
donné par:
 avec avec  (10.33)
(10.33)
c'est-à-dire que les solutions de la forme:
 (10.34)
(10.34)
où  est
une "solution particulière" de est
une "solution particulière" de  et et  la "solution
homogène",
parcourent toutes les solutions de l'E.D. la "solution
homogène",
parcourent toutes les solutions de l'E.D.
Démonstration:
La première affirmation sera supposée évidente.
En ce qui concerne la 2ème partie, toute fonction de
la forme  est
solution de est
solution de  . .
En effet c'est trivial et cela découle de la définition du concept
de noyau (cf. chapitre de Théorie Des Ensembles):
 (10.35)
(10.35)
 C.Q.F.D. C.Q.F.D.
Ce qu'il est important aussi de comprendre avec
les E.D. linéaires avec second membre, c'est
que si nous trouvons des solutions à L(y)
avec un second membre donné et des solutions à la même E.D. avec
un autre second membre (différent!), alors la somme de toutes ces
solutions, sera solution de l'E.D. avec la somme des seconds membres!!!
Il existe de nombreuses manières de résoudre
les équations différentielles linéaires ou
non linéaires de manière exacte ou approchée.
Citons les quelques méthodes que nous analyserons plus
loin par l'exemple (mais qui se trouvent déjà de
très très nombreuses fois dans les chapitres de physique):
- La "méthode du
polynôme caractéristique des E.D."
(voir plus bas) utilisée un peu dans tous les chapitre de Physique/Chimie
du présent site.
- La "méthode du
facteur intégrant" (voir
plus bas) pour la culture générale mais utilisée à ce jour sur aucun
cas pratique du site.
- La "méthode de variation de
la constante" (voir plus bas) et utilisée à ce jour
uniquement dans le chapitre de Génie Industriel.
- La "méthode des
perturbations des E.D." (voir
plus bas) utile pour la physique quantique ondulatoire et le physique
quantique des champs.
Signalons également d'autres méthodes
très utilisées
(grands classiques scolaires) mais qui sont prinicpalement traitées
au cas par cas dans les différents
chapitres du site car les approches de résolution sont trop
nombreuses et particulières:
- La "méthode de
séparation des
variables E.D." (équation
de la chaleur dans le chapitre de Thermodynamique, équation
des vagues dans le chapitre de Génie Marin & Météo, équation
d'évolution de
Schrödinger dans le chapitre de Physique Quantique Ondulatoire,
vibration d'un tambour dans le chapitre de Mécanique Ondulatoire)
dont nous verrons un cas très particulier et simple plus bas mais
pour laquelle il vaut mieux se référer aux chapitres mentionnés
pour des exemples concrets.
- La "méthode matricielle
de résolution des E.D."
et "solution
triviales des E.D." (modèle
de Lotka-Volterra dans le chapitre de Dynamique des Populations,
résonance de spin électronique ou nucléaire dans le chapitre de
Physique Quantique Relativiste, modèle de Lorenz dans le chapitre
de Génie Marin & Météo).
- La "méthode spectrale" utilisant le théorème spectral
démontré dans le chapitre d'Algèbre Linéaire (voir le chapitre
de Génie Industriel dans le calcul de fiabilité de système par
chaînes de Markov pour un exemple concret).
- La "méthode de
la transformée
de Fourier des E.D."
ou la "méthode de la transformée
de Laplace des E.D." (équation de la chaleur
dans le chapitre d'Analyse Fonctionnelle, résolution de
l'équation de Black & Scholes
dans le chapitre d'Économie, équation de la poutre sous
charge ponctuelle dans le chapitre de Génie Civil)
- Les "méthodes numériques
des E.D." pour résoudre
les équations différentielles avec l'ordinateur quand elles n'ont
pas de solutions analytique connues (équation de la chaleur dans
le chapitre de Méthodes Numériques).
MÉTHODE DU POLYNÔME CARACTÉRISTIQUE
La résolution des équations différentielles
simples (à coefficients
constants et sans second membre la plupart du temps...) utilise
une technique faisant appel à un polynôme caractéristique
de l'équation
différentielle
dont
nous verrons les détails dans les développements à suivre
sur quelques cas particuliers courants en physique.
C'est une méthode relativement simple à mettre
en place lorsque nous cherchons les solutions homogènes
de l'équation sans second
membre (ESSM). Dans le cas contraire, celui de la présence
d'un second membre, nous additionnons les solutions de l'équation
homogènes
aux solutions particulières.
RÉSOLUTION L'E.H. DE L'E.D.L. À COEFFICIENTS CONSTANTS
D'ORDRE 1
Considérons l'E.D.L. à coefficients constants suivante:
 (10.36)
(10.36)
qui est une version simplifiée de l'E.D.L à coefficients
constants générale suivante:
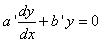 (10.37)
(10.37)
où:
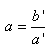 (10.38)
(10.38)
Nous écrivons son équation homogène (ESSM)
associée:
 (10.39)
(10.39)
Ce qui peut s'écrire:
 (10.40)
(10.40)
d'où:
 (10.41)
(10.41)
Il y a derrière cette solution homogène une infinité de solutions: à chaque valeur donnée à C correspond une solution.
Il faut encore à cette solution homogène ajouter la solution particulière  et
nous disposons pour cela d'une collection de recettes, qui dépendent
du type de la fonction f(x) du second membre de l'équation.
Nous les verrons au cas par cas dans les différents chapitres de
Physique. et
nous disposons pour cela d'une collection de recettes, qui dépendent
du type de la fonction f(x) du second membre de l'équation.
Nous les verrons au cas par cas dans les différents chapitres de
Physique.
RÉSOLUTION DE L'E.H. DE L'E.D.L. À COEFFICIENTS NON CONSTANTS
DE L'E.D.L D'ORDRE 1
La solution générale des équations différentielles linéaires
homogènes (ESSM) d'ordre 1 à coefficients non constants:
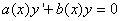 (10.42)
(10.42)
peut toujours se réduire à la forme suivante:
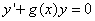 (10.43)
(10.43)
où:
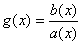 (10.44)
(10.44)
Bon évidemment il y a la solution 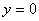 ...
mais cherchons à faire mieux. Nous avons donc: ...
mais cherchons à faire mieux. Nous avons donc:
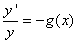 (10.45)
(10.45)
Il vient donc:
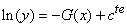 (10.46)
(10.46)
où G(x) est une primitive de g(x).
Dès lors:
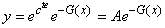 (10.47)
(10.47)
Il est aussi fréquent de retrouver ces développements
sous une autre écriture un tout petit peu plus explicite qui est
la suivante:
Nous repartons donc de l'équation différentielle
sans seconde membre à coefficients non constante:
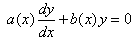 (10.48)
(10.48)
après réarrangement:
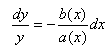 (10.49)
(10.49)
Et donc:
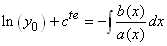 (10.50)
(10.50)
Soit:
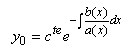 (10.51)
(10.51)
Ce résultat nous sera très utile pour calculer
la transformée de Fourier d'une fonction Gaussienne (cf. chapitre
Suite Et Séries), transformée de Fourier qui
est indispensable pour résoudre de manière assez
générale l'équation
de la Chaleur
(cf. chapitre de Thermodynamique),
résolution qui nous permettra
enfin de démontrer l'équation de Black & Scholes
(cf.
chapitre d'Économie).
RÉSOLUTION L'E.H. DE L'E.D.L. À COEFFICIENTS CONSTANTS
D'ORDRE 2
Considérons l'E.D.L. à coefficients constants suivante:
 (10.52)
(10.52)
qui est une version simplifiée de l'E.D.L à coefficients
constants générale suivante:
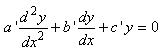 (10.53)
(10.53)
où:
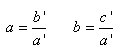 (10.54)
(10.54)
Nous écrivons son équation homogène (ESSM)
associée:
 (10.55)
(10.55)
dans laquelle la fonction du second membre est nulle. Nous pouvons
assez rapidement entrevoir une solution du type (en s'inspirant
de la forme des solutions des E.D. du 1er ordre):
 (10.56)
(10.56)
où  est
une constante. Ce qui nous donne alors: est
une constante. Ce qui nous donne alors:
 (10.57)
(10.57)
Ce que nous pouvons simplifier en:
 (10.58)
(10.58)
Si notre hypothèse de départ est bonne, nous n'avons qu'à résoudre
en K cette "équation caractéristique" (ECAR)
ou "polynôme
caractéristique" de l'équation homogène pour trouver
la solution homogène:
 (10.59)
(10.59)
dont les solutions dépendent du signe du discriminant du polynôme
caractéristique:
 (10.60)
(10.60)
- Si le discriminant est strictement positif, soit  : :
Alors nous savons que le polynôme caractéristique possède deux
racines distinctes et nous avons alors:
 (10.61)
(10.61)
où  et et  .
Nous disons alors que la solution est "retardée" ou "avancée" selon
les valeurs de ces constantes. Mais l'essentiel est de remarquer
que si .
Nous disons alors que la solution est "retardée" ou "avancée" selon
les valeurs de ces constantes. Mais l'essentiel est de remarquer
que si  est
solution, alors est
solution, alors  est
toujours solution! est
toujours solution!
Nous parlons alors de "solution générale de l'équation homogène".
Il y a derrière ce résultat une infinité de solutions: à chaque
valeur donnée aux constantes A, B correspond une
solution.
Les physiciens écrivent aussi parfois cela sous une forme particulière
en posant d'abord:
 (10.62)
(10.62)
avec donc:
 (10.63)
(10.63)
Et en utilisant les fonctions de trigonométrie hyperbolique
(cf. chapitre de Trigonométrie):
 (10.64)
(10.64)
d'où finalement la possibilité d'écrire la solution homogène sous
la forme (lorsque nous omettons l'avance ou le retard  ): ):
 (10.65)
(10.65)
Par ailleurs, montrons que les solutions de l'ESSM forment un
espace vectoriel de dimension 2 (correspond donc à l'ordre de notre
E.D.)!
En effet:
- La fonction zéro:  est
solution de l'ESSM (ça c'est inutile de le démontrer... évident!). est
solution de l'ESSM (ça c'est inutile de le démontrer... évident!).
- La somme ou soustraction des solutions reste solution (ça nous
l'avons déjà démontré plus haut)
- Les éléments de la base de l'espace vectoriel (les solutions
de l'ESSM) sont linéairement indépendants (ça c'est intéressant
car nous en aurons besoin!).
Posons:
 (10.66)
(10.66)
Alors:
 (10.67)
(10.67)
Ces relations injectées dans l'ESSM sous forme généralisée:
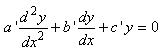 (10.68) (10.68)
donne alors:
 (10.69)
(10.69)
Donc nous avons bien une structure d'espace vectoriel.
Rappelons que inversement deux fonctions sont linéairement
dépendantes
si:
 (10.70)
(10.70)
- Si le discriminant est nul, soit  : :
L'équation caractéristique possède une racine double réelle K.
En allant un peu vite nous dirons alors:
 (10.71)
(10.71)
et que c'est fini... mais au fait ce serait oublier que la base
vectorielle doit être formée de deux solutions indépendantes!
Donc la deuxième solution est probablement... de la forme:
 (10.72)
(10.72)
Alors:
 (10.73)
(10.73)
Si nous l'injectons cela dans l'ESSM sous forme généralisée:
 (10.74)
(10.74)
alors:
 (10.75)
(10.75)
Soit dans notre cas:
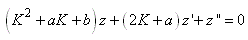 (10.76)
(10.76)
Or, les deux valeurs de K réelles sont justement
solutions de:
 (10.77)
(10.77)
La relation antéprécédente se réduit alors à:
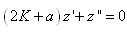 (10.78)
(10.78)
et comme nous sommes dans le cas d'étude où le
discriminant est nul, il vient:
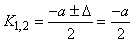 (10.79)
(10.79)
Donc la relation antéprécédente se réduit au final à:
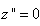 (10.80)
(10.80)
Nous en déduisons:
 (10.81)
(10.81)
Donc finalement:
 (10.82)
(10.82)
Ce qui donne pour la solution générale de l'ESSM:
 (10.83)
(10.83)
- Si le discriminant est négatif, soit  : :
L'équation caractéristique possède deux racines complexes conjuguées
(cf. chapitre d'Algèbre):
 (10.84)
(10.84)
Dès lors:
 (10.85)
(10.85)
Or, si nous cherchons plutôt des solutions réelles, nous pouvons
toujours poser A et B égaux tels que:
 (10.86)
(10.86)
Et si nous posons que le retard et respectivement l'avance sont
nuls ( ),
alors nous retrouvons la relation disponible dans la plupart des
livres: ),
alors nous retrouvons la relation disponible dans la plupart des
livres:
 (10.87)
(10.87)
où A' et B' sont donc deux constantes réelles
quelconques. Il existe une autre forme importante à cette dernière
relation (souvent utilisée en électronique par exemple).
Effectivement, Il est possible, pour tout A' et B'
réels,
de trouver C' et  réels
tels que l'égalité suivante soit vérifiée: réels
tels que l'égalité suivante soit vérifiée:
 (10.88)
(10.88)
Nous posons:
 (10.89)
(10.89)
alors:
 (10.90)
(10.90)
Il est alors possible de trouver  tel
que: tel
que:
 et et  (10.91)
(10.91)
La quantité de départ s'écrit ainsi:
 (10.92)
(10.92)
Finalement:
 (10.93)
(10.93)
Nous pouvons donc faire le résumé suivant:
Tableau: 28.1 - Solutions types de l'E.H. de l' L'E.D.L. à coefficients constants
MÉTHODE DU FACTEUR INTÉGRANT (D'EULER)
La technique du facteur d'intégration est utile lorsqu'il
s'agit de résoudre des équations différentielles
de la forme:
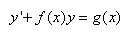 (10.94)
(10.94)
Nous n'avons pas à ce jour de cas pratique
d'application de cette technique dans les autres chapitres du site.
Il faut donc voir cela comme une présentation pour la culture
générale.
L'idée de base étant de trouver une
fonction 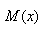 , appelée "facteur
d'intégration",
par laquelle peut être multipliée notre équation
différentielle pour ramener le terme de gauche de l'égalité à une
simple dérivée. Par exemple, pour une équation
différentielle linéaire comme celle ci-dessus, nous
choisissons assez souvent le facteur d'intégration suivant
(mais ce n'est de loin pas la seule possibilité et ce choix
ne permet pas de tout résoudre!): , appelée "facteur
d'intégration",
par laquelle peut être multipliée notre équation
différentielle pour ramener le terme de gauche de l'égalité à une
simple dérivée. Par exemple, pour une équation
différentielle linéaire comme celle ci-dessus, nous
choisissons assez souvent le facteur d'intégration suivant
(mais ce n'est de loin pas la seule possibilité et ce choix
ne permet pas de tout résoudre!):
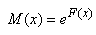 (10.95)
(10.95)
Nous avons alors:
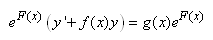 (10.96)
(10.96)
ou en distribuant:
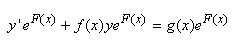 (10.97)
(10.97)
Ce qui peut donc être vu comme:
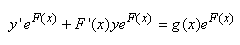 (10.98)
(10.98)
ou encore plus fort (et c'est là que réside toute
l'astuce)...:
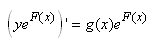 (10.99)
(10.99)
Nous pouvons alors prendre la primitive par rapport à x:
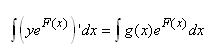 (10.100)
(10.100)
et trivialement (!) nous avons la primitive de gauche
qui est immédiate:
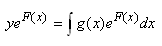 (10.101)
(10.101)
Soit:
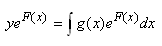 (10.102)
(10.102)
Ce qui est parfois écrit:
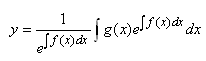 (10.103)
(10.103)
 Exemple: Exemple:
Considérons l'équation différentielle:
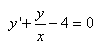 (10.104)
(10.104)
Que nous mettrons sous la forme:
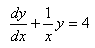 (10.105)
(10.105)
Nous voyons alors que (en assumant que x soit strictement
positif):
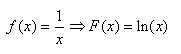 (10.106)
(10.106)
Nous avons alors:
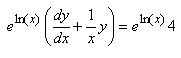 (10.107)
(10.107)
Hasard faisant (l'exemple est exprès simple),
nous avons cette égalité qui se simplifie puisque:
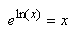 (10.108)
(10.108)
en:
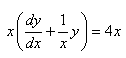 (10.109)
(10.109)
Ce qui peut se condenser en:
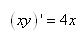 (10.110)
(10.110)
En intégrant:
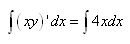 (10.111)
(10.111)
Il vient alors immédiatement:
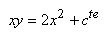 (10.112)
(10.112)
Soit: 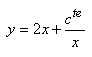 (10.113)
(10.113)
MÉTHODE DE SÉPARATION DES VARIABLES
La méthode de séparation des variables
est une technique très fréquente en physique dès
que nous avons des équations différentielles du deuxième
ordre. De nombreux exemples très complets et pratiquent
se trouvent déjà de part et d'autres dans les différents
chapitres déjà précédemment mentionnés.
Nous allons ici juste en présenter un cas particulier par
principe juste histoire de bien faire les choses mais au minimum
vital!
Considérons le cas fréquent en physique
d'équation différentielle partielle du type:
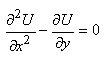 (10.114)
(10.114)
La solution de cette équation nécessite
donc de trouver une fonction U qui dépende de x et
de y tel que:
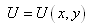 (10.115)
(10.115)
En physique, l'idée consiste alors à poser
que nous pouvons toujours trouver une solution dite séparable
de la forme:
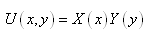 (10.116)
(10.116)
Ainsi, l'équation différentielle s'écrit:
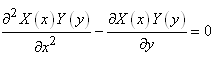 (10.117)
(10.117)
Ce qui peut se simplifier en:
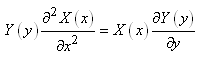 (10.118)
(10.118)
Après réarrangement est il d'usage
en physique de noter cette dernière égalité sous
la forme condensée:
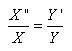 (10.119)
(10.119)
Cette égalité ne peut avoir lieu que
si chacun des termes est une constante puisque X ne dépend
que de x et Y que de y. Il vient alors:
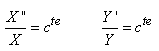 (10.120)
(10.120)
Et chaque équation différentielle
par alors être résolue indépendamment de l'autre
et une fois les solutions trouvées on les multiplie pour
donc déterminer l'expression de U.
MÉTHODE DE VARIATION DE LA CONSTANTE
L'idée de la méthode de variation
de la constante est la suivante: si nous avons une solution particulière
affectée de constantes, nous savons qu'en fonction des conditions
initiales celles-ci sont bien déterminées. L'idée
est alors de généraliser en posant que ces constantes
sont des fonctions. Dans certains cas évidemment les développements
mathématiques montreront que les fonctions sont obligatoirement
des constantes.
L'idée sous-jacente de cette méthode, c'est de se
dire que les solutions de l'équation différentielle
(linéaire) avec second membre vont ressembler aux solutions
de l'équation homogène. Comme le terme de droite
va perturber cette solution, nous faisons varier uniquement les
constantes (qui n'en seront plus), mais nous restons sur la "base" des
solutions homogènes, pour chercher des solutions proches.
Après, nous vérifions que ce raisonnement à la
physicienne donne bien toutes les solutions de l'équation.
Voyons avant de passer au cas général un exemple simple
en considérant
l'équation
différentielle suivante:
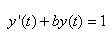 (10.121)
(10.121)
pour laquelle la solution particulière de
l'équation homogène (ESSM) est:
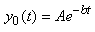 (10.122)
(10.122)
La méthode de variation de la constante consiste
alors à poser:
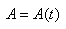 (10.123)
(10.123)
et donc:
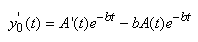 (10.124)
(10.124)
Or de par l'équation différentielle
avec second membre, nous avons:
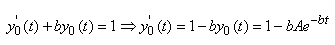 (10.125)
(10.125)
Donc en utilisant les deux dernières relations
il vient:
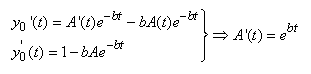 (10.126)
(10.126)
et il s'ensuit que:
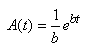 (10.127)
(10.127)
où nous avons éliminé la constante
d'intégration parce que nous voulons c'est une solution
particulière! La solution générale particulière
(pg) est alors la somme de la solution particulière homogène
et celle avec la variation de la constante:
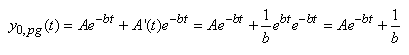 (10.128)
(10.128)
Ainsi, en généralisant l'exemple précédent,
nous avons donc une équation différentielle de la
forme:
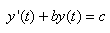 (10.129)
(10.129)
La solution particulière générale
sera alors:
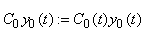 (10.130)
(10.130)
Nous avons alors:
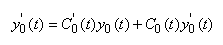 (10.131)
(10.131)
d'où injecté dans l'équation
différentielle d'origine:
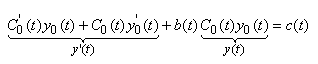 (10.132)
(10.132)
Soit après factorisation des termes semblables:
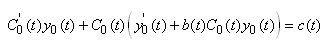 (10.133)
(10.133)
Nous avons donc la relation ci-dessus et la solution
particulière à l'équation différentielle
homogène (donc sans seconde membre):
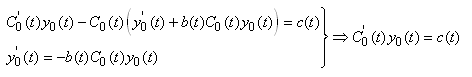 (10.134)
(10.134)
Nous trouvons donc:
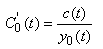 (10.135)
(10.135)
et il suffit alors d'intégrer cette équation pour
trouver 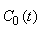 . Ensuite, la solution générale particulière
(pg) est alors la somme de la solution particulière homogène
et de celle avec la variation de la constante. . Ensuite, la solution générale particulière
(pg) est alors la somme de la solution particulière homogène
et de celle avec la variation de la constante.
SYSTÈMES D'ÉQUATIONS DIFFÉRENTIELLES
Voyons maintenant des développements particuliers qui vont
aussi bien être utiles en physique quantique que dans la résolution
de systèmes particuliers d'équations différentielles
(et particulièrement une qui est connue en théorie
du chaos!).
Indiquons d'abord au lecteur avant d'aller plus loin que le cas
plus complexe non homogène (avec seconde membre) et avec
coefficients inconnus est traité directement par l'exemple
dans le chapitre de Génie Industriel lors du traitement
de la fiabilité d'un système réparable sous
la forme d'une chaîne de Markov avec traitement par les déterminants
et valeurs/vecteurs propres.
Pour commencer cette première approche, il va nous falloir
introduire le concept d'exponentiation d'une matrice:
L'ensemble des matrices  à coefficients
dans à coefficients
dans  noté noté  est
un espace vectoriel pour l'addition des matrices et la multiplication
par un scalaire. Nous notons I la matrice identité. est
un espace vectoriel pour l'addition des matrices et la multiplication
par un scalaire. Nous notons I la matrice identité.
Nous admettrons qu'une suite de matrices  converge
vers une matrice A si et seulement si les suites de coefficients
des matrices converge
vers une matrice A si et seulement si les suites de coefficients
des matrices  convergent
vers les coefficients correspondants de A. convergent
vers les coefficients correspondants de A.
 Exemple: Exemple:
Dans  la
suite de matrices: la
suite de matrices:
 (10.136)
(10.136)
converge vers:
 (10.137)
(10.137)
lorsque . .
Si ,
nous avons vu lors de notre étude des nombres complexes
(cf. chapitre sur les Nombres) que
la série: ,
nous avons vu lors de notre étude des nombres complexes
(cf. chapitre sur les Nombres) que
la série:
 (10.138)
(10.138)
converge et sa limite est notée  .
En fait ici il n'y a aucune difficulté à remplacer x par
une matrice A puisque nous savons (nous l'avons montré lors
de notre étude des nombres complexes) que tout nombre complexe
peut s'écrire sous la forme suivante (le corps des nombres
complexes est donc isomorphe au corps des matrices réelles
carrées de dimensions 2 ayant cette forme): .
En fait ici il n'y a aucune difficulté à remplacer x par
une matrice A puisque nous savons (nous l'avons montré lors
de notre étude des nombres complexes) que tout nombre complexe
peut s'écrire sous la forme suivante (le corps des nombres
complexes est donc isomorphe au corps des matrices réelles
carrées de dimensions 2 ayant cette forme):
 (10.139)
(10.139)
et qu'un nombre complexe au carré est équivalant à mettre
sa forme matricielle au carré:
 (10.140)
(10.140)
Effectivement:
 (10.141)
(10.141)
Nous définissons alors l'exponentielle d'une matrice  comme
la matrice limite de la suite: comme
la matrice limite de la suite:
 (10.142)
(10.142)
Si la matrice A est diagonale il est évident que
son exponentielle est facile à calculer. En effet, si:
 (10.143)
(10.143)
Par suite:
 (10.144)
(10.144)
Or, il apparaît évident qu'une matrice non diagonale
va être beaucoup plus compliquée à traiter! Nous
allons alors utiliser la technique de diagonalisation soit une
réduction des endomorphismes (cf.
chapitre d'Algèbre Linéaire).
Alors, remarquons que si  est
inversible et si est
inversible et si  alors: alors:
 (10.145)
(10.145)
Ceci découle du fait que (penser au changement de base
d'une application linéaire comme ce qui a été étudié dans
le chapitre d'Algèbre Linéaire):
 (10.146)
(10.146)
Donc:
 (10.147)
(10.147)
Ce développement va nous permettre de ramener le calcul
de l'exponentielle d'une matrice diagonalisable à la recherche
de ses valeurs propres et de ses vecteurs propres.
 Exemple: Exemple:
Calculons  où: où:
 (10.148)
(10.148)
Les valeurs propres de A sont , ,  et
les vecteurs propres associés sont: et
les vecteurs propres associés sont:
 (10.149)
(10.149)
Effectivement:
 et et  (10.150)
(10.150)
En posant:
 (10.151)
(10.151)
Nous avons:
 (10.152)
(10.152)
avec:
 (10.153)
(10.153)
Par conséquent:
 (10.154)
(10.154)
Maintenant, rappelons que dans le cas des nombres réels
nous savons que si  alors: alors:
 (10.155)
(10.155)
Dans le cas des matrices nous pouvons montrer que si  sont
deux matrices qui commutent entre-elles c'est-à-dire telles
que sont
deux matrices qui commutent entre-elles c'est-à-dire telles
que  ,
alors: ,
alors:
 (10.156)
(10.156)
La condition de commutativité tient au fait que l'addition
dans l'exponentielle est quant à elle commutative. La démonstration
est donc intuitive.
Un corollaire important de cette proposition est que pour toute
matrice , ,  est
inversible. En effet les matrices est
inversible. En effet les matrices  et et  commutent,
par conséquent: commutent,
par conséquent:
 (10.157)
(10.157)
Nous rappelons qu'une matrice  à coefficients
complexes est unitaire si: à coefficients
complexes est unitaire si:
 (10.158)
(10.158)
La proposition suivante nous servira par la suite.
Montrons que si A est une matrice hermitienne (dite aussi "autoadjointe")
(cf. chapitre d'Algèbre Linéaire)
alors pour tout  , ,  est
unitaire. est
unitaire.
Démonstration:
 (10.159)
(10.159)
Donc:
 (10.160)
(10.160)
C.Q.F.D.
Rappelons que cette condition pour une matrice autoadjointe est
liée à la définition de groupe unitaire d'ordre n (cf.
chapitre d'Algèbre Ensembliste).
Une des premières applications de l'exponentielle de matrices
est la résolution des équations différentielles
ordinaires. En effet, de l'équation différentielle
linéaire ci-dessous avec comme condition initiale  et
où A est une matrice: et
où A est une matrice:
 (10.161)
(10.161)
la solution est donnée (cf. chapitre
de Calcul Différentiel et Intégral) par:
 (10.162)
(10.162)
Nous retrouvons fréquemment ce genre de systèmes
d'équations différentielles en biologie (dynamique
des populations), en astrophysique (étude des plasmas) ou
en mécanique des fluides (théorie du chaos) ainsi
qu'en mécanique classique (systèmes couplés),
en astronomie (orbites couplées), en électrotechnique,
etc.
 Exemple: Exemple:
Supposons que nous ayons le système d'équations
différentielles homogène (sans termes constants)
suivant:
 (10.163)
(10.163)
La matrice associée est alors:
 (10.164)
(10.164)
et son exponentielle (voir les développements faits plus
haut):
 (10.165)
(10.165)
La solution générale du système est donc:
 (10.166)
(10.166)
Nous avons donc:
 (10.167)
(10.167)
En calculant la dérivée des relations précédentes
et en comparant à:
 (10.168)
(10.168)
nous déterminons facilement les constantes pour obtenir:
 (10.169)
(10.169)
ce qui nous donne finalement:
 (10.170)
(10.170)
MÉTHODE RÉGULIÈRE DES PERTURBATIONS
Très fréquemment en physique (de pointe), un problème
mathématique
ne peut pas être résolu de manière exacte. Si la
solution est connue il y a parfois une telle dépendance
de paramètres que la solution
est difficile à utiliser en tant que telle.
Il peut arriver cependant qu'un paramètre identifié de
l'équation différentielle, que nous noterons par
tradition avec la lettre grecque  ,
soit tel que la solution soit disponible et raisonnablement
simple pour ,
soit tel que la solution soit disponible et raisonnablement
simple pour  . .
Le souci ensuite est de savoir comment la solution est altérée
pour un  non-nul
mais petit quand même. Cette étude est le centre de la
théorie des
perturbations que nous utilisons par exemple dans le chapitre de
relativité générale pour calculer la précession
du périhélie de
Mercure. non-nul
mais petit quand même. Cette étude est le centre de la
théorie des
perturbations que nous utilisons par exemple dans le chapitre de
relativité générale pour calculer la précession
du périhélie de
Mercure.
Comme la théorie dans le cadre général est trop complexe par rapport
aux objectifs du site, nous nous proposons une approche par l'exemple
d'abord avec une simple équation algébrique et ensuite
avec ce qui nous intéresse: une E.D.
THÉORIE PERTURBATIVE DES ÉQUATIONS ALGÉBRIQUES
Considérons l'équation polynômiale suivante:
 (10.171)
(10.171)
Nous savons de par notre étude du chapitre d'analyse fonctionnelle,
que cette équation polynômiale admet deux racines qui sont trivialement:
 (10.172)
(10.172)
Pour  petit,
ces racines peuvent être approximées par le premier terme en développement
de série de Taylor (cf. chapitre de Suites
Et Séries): petit,
ces racines peuvent être approximées par le premier terme en développement
de série de Taylor (cf. chapitre de Suites
Et Séries):
 (10.173)
(10.173)
La question et de savoir si nous pouvons obtenir les deux relations
précédentes sans a priori de connaissances sur la solution exacte
de l'équation polynômiale initiale? La réponse est bien évidemment
affirmative avec l'aide de la théorie des perturbations.
La technique se base en quatre étapes:
1. Dans la première étape, nous assumons que la
solution de l'équation
polynomiale est une expression du type série de Taylor en  .
Nous avons alors: .
Nous avons alors:
 (10.174)
(10.174)
où  sont
bien évidemment à déterminer. sont
bien évidemment à déterminer.
2. Dans la deuxième étape, nous injectons la solution hypothétique
dans notre équation polynômiale:
 (10.175)
(10.175)
Comme:

(10.176)
et:
 (10.177)
(10.177)
Il vient finalement que l'équation polynômiale s'écrit:
 (10.178)
(10.178)
3. Dans la troisième étape nous égalisons successivement les termes
avec 0 tel que:
 (10.179)
(10.179)
4. Quatrième et dernière étape, nous résolvons successivement
les équations polynômiales ci-dessus pour obtenir:
 (10.180)
(10.180)
En injectant ces résultants dans la solution hypothétique:
 (10.181)
(10.181)
il est évident d'observer que nous retombons sur la solution certaine:
 (10.182)
(10.182)
THÉORIE PERTURBATIVE DES ÉQUATIONS DIFFÉRENTIELLES
La théorie des perturbations est aussi souvent utilisée pour résoudre
un bon nombre d'équations différentielles. C'est le cas par exemple
en mécanique des fluides, en relativité générale ou en physique
quantique.
A nouveau, plutôt que de faire une théorie ultra abstraite et
générale, voyons le concept sur un exemple tel que précédemment.
Considérons l'équation différentielle suivante:
 (10.183)
(10.183)
ou autrement écrit:
 (10.184)
(10.184)
avec les conditions aux limites:
 (10.185)
(10.185)
La résolution exacte est relativement facile à obtenir:
D'abord
nous commençons par l'équation homogène:
 (10.186)
(10.186)
C'est donc une équation différentielle linéaire d'ordre 2 avec
des coefficients constants, équation qu'il est relativement aisé
de résoudre dans le cas général. Soit l'équation:
 (10.187)
(10.187)
Supposons que la fonction y qui satisfait cette équation
différentielle soit de la forme  où
K peut être un nombre complexe. Nous avons alors: où
K peut être un nombre complexe. Nous avons alors:
 ou ou
 (10.188)
(10.188)
pourvu, bien sûr, que  .
Cette dernière relation est donc l'équation quadratique auxiliaire
de l'équation différentielle (polynôme caractéristique). Elle
a deux solutions/racines (c'est une simple résolution d'un polynôme
du deuxième degré) que nous noterons dans le cas général: .
Cette dernière relation est donc l'équation quadratique auxiliaire
de l'équation différentielle (polynôme caractéristique). Elle
a deux solutions/racines (c'est une simple résolution d'un polynôme
du deuxième degré) que nous noterons dans le cas général:  .
Ce qui signifie que: .
Ce qui signifie que:
 et et
 (10.189)
(10.189)
sont satisfaites pour les deux racines. Si nous faisons la somme
puisque les deux sont égales à la même constante:
 (10.190)
(10.190)
Ainsi, il est immédiat que la solution générale de l'équation
homogène de y est du type:
 (10.191)
(10.191)
où A, B sont bien évidemment des constantes à déterminer.
Nous résolvons maintenant le polynôme caractéristique:
 (10.192)
(10.192)
Il vient immédiatement que:
 (10.193)
(10.193)
Donc:
 (10.194)
(10.194)
Maintenant une solution particulière à:
 (10.195)
(10.195)
est relativement trivialement une solution du type:
 (10.196)
(10.196)
où B est bien évidemment une constante à déterminer et
qui vaut simplement une fois injectée dans l'équation différentielle:
 (10.197)
(10.197)
Soit:
 (10.198)
(10.198)
D'où finalement la solution générale:
 (10.199)
(10.199)
Ensuite, avec les conditions initiales qui sont pour rappel
 (10.200)
(10.200)
il
est très facile de trouver A:
 (10.201)
(10.201)
Nous avons aussi:
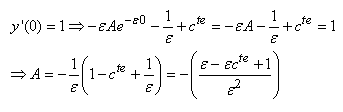 (10.202)
(10.202)
Il est loisible de choisir que 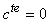 ce
qui nous donne: ce
qui nous donne:
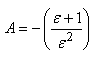 (10.203)
(10.203)
Dès lors:
 (10.204)
(10.204)
devient:
 (10.205)
(10.205)
Maintenant que nous avons la solution générale, si  est
petit nous pouvons prendre le développement d'ordre 4 en série
de Maclaurin de l'exponentielle (cf. chapitre
de Suites Et Séries). Tel que: est
petit nous pouvons prendre le développement d'ordre 4 en série
de Maclaurin de l'exponentielle (cf. chapitre
de Suites Et Séries). Tel que:
 (10.206)
(10.206)
Injecté dans y cela donne (vous remarquerez que
nous exprimons parfois explicitement par anticipation...... le
terme d'ordre 5):
 (10.207)
(10.207)
Maintenant que nous avons ce développement, ce que nous souhaitons
montrer c'est qu'à partir d'un développement perturbatif nous pouvons
retrouver le même résultat en série et ce sans aucune connaissance
préalable sur la solution.
A nouveau, le développement pour cela se fait en 4 étapes:
1. Dans la première étape, nous assumons que la
solution de l'équation
différentielle est une expression du type série de
Taylor en  .
Nous avons alors: .
Nous avons alors:
 (10.208)
(10.208)
où  sont
bien évidemment à déterminer. sont
bien évidemment à déterminer.
2. Dans la deuxième étape, nous injectons la solution
hypothétique
de notre équation différentielle dans celle-ci avec
les conditions initiales et nous développons le tout.
D'abord l'équation différentielle:
 (10.209)
(10.209)
ensuite les conditions initiales:
 (10.210)
(10.210)
3. Dans la troisième étape nous égalisons successivement les termes
avec 0 tel que:
 (10.211)
(10.211)
4. Dans la quatrième étape nous résolvons les équations
différentielles
listées précédemment (si vous ne voyez pas comment nous les résolvons
n'hésitez pas à nous contacter!):
 (10.212)
(10.212)
En injectant ces relations dans la solution supposée développée
en série de Taylor et injectée dans l'équation différentielle:
 (10.213)
(10.213)
Nous retombons sur:
 (10.214)
(10.214)

- Calcul différentiel et intégral (Tome
I), N. Piskunov, Édition Mir (Moscou),
ISBN10: 2729893407 (511 pages) - Imprimé en 1972
- Calcul différentiel
et intégral (Tome II),
N. Piskunov, Édition Mir (Moscou), ISBN10: 2729893415 (616
pages) - Imprimé en 1972
- Calcul différentiel
et intégral (Tome I), J. Douchet + B.
Zwahlen, Éditions Presses polytechniques et romandes,
ISBN10: 2880741963 (244 pages) - Imprimé en 2007
- Calcul différentiel
et intégral (Tome II), J. Douchet + B.
Zwahlen, Éditions Presses polytechniques et romandes,
ISBN10: 2880742579 (172 pages) - Imprimé en 2007
- Advanced Engineering Mathematics
with MATLAB (Third Edition), Dean G. Duffy, CRC
Press Inc, ISBN13: 9781439816240 (1105 pages) - Imprimé en
2010
|