News :: Erreur :: Statistiques :: ClearType :: Imprimer

GÉNIE MARIN & MÉTÉO | GÉNIE MÉCANIQUE | GÉNIE ÉLECTRIQUE
GÉNIE ÉNERGÉTIQUE| GÉNIE CIVIL | GÉNIE BIOLOGIQUE | GÉNIE AÉRONAUTIQUE
GÉNIE SPATIAL | GÉNIE CHIMIQUE | GÉNIE INDUSTRIEL

LISTE DES SUJETS TRAITÉS SUR CETTE PAGE

ÉQUATION FONDAMENTALE DE LA PROPULSION

Un lanceur spatial a pour mission de placer une charge en orbite, pour cela il doit fonctionner dans l'atmosphère et le vide. Les principes utilisés sont ceux de l'action et de la réaction de Newton, et de la conservation de la quantité de mouvement : grossièrement nous pouvons affirmer qu'une fusée accélère en éjectant des gaz à grande vitesse (le ballon baudruche qui se dégonfle donne une bonne idée du phénomène). Après une étude mécanique simple nous pouvons obtenir l'équation fondamentale de la propulsion.

En considérant les différentes parties mobiles et indépendantes de la fusée (en fait la structure principale séparément des gaz éjectés), nous pouvons affirmer à l'aide du principe d'action et réaction (cf. chapitre de Mécanique classique) pour un système donné, la somme des forces extérieures est:

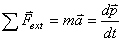  (1)

Ainsi, en prenant le système fusée et gaz ensembles nous avons:

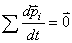  (2)

Soit que:

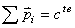  (3)

Le principe de la propulsion s'énonce alors grâce à la conservation de la quantité de mouvement, que nous avons établie.

Considérons une fusée de masse m et de vitesse 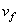, la vitesse d'éjection des gaz étant 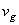. Au temps t, nous avons :

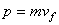  (4)

au temps t+dt nous avons:

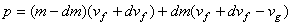  (5)

mais le dm est une perte de masse donc il faut changer son signe sinon la relation précédente ne correspond pas à l'interprétation de la réalité. Ainsi:

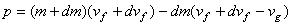
d'après le principe de conservation de la quantité de mouvement:

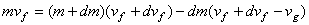  (1)

d'où après simplification:

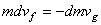  (2)

d'où:

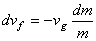  (3)

ce qui par intégration donne "l'équation fondamentale de la propulsion" par fusée hors champ de gravité et dans le vide à vitesse d'éjection constante des gaz...:

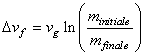  (4)

Nous en déduisons donc qu'un lanceur accélère d'autant plus que la vitesse des gaz est grande, que la poussée dépend de la quantité de gaz fournis et de leur vitesse, et la rapport des masses initiale et finale doit être maximum pour favoriser la propulsion, c'est-à-dire que la structure du système est voulue négligeable (la masse finale est alors minimale).

Cependant dans un champ gravitationnel il faut ajouter le terme qui freine la fusée et qui donnera donc l'expression:

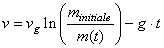  (5)

si nous supposons la gravité g comme constante pendant la phase d'accélération principale.

Exemple:

La fusée Saturne 5 a une poussée totale d'environ 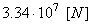 et, au départ, une masse totale de 3'038 tonnes. La premier étage consomme 2'000 tonnes de carburant en comburant en 150 [s] (seulement le premier étage!). La vitesse d'éjection des gaz est de .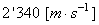 

Si nous négligeons le poids propre de la cellule du premier étage, la vitesse en fin de combustion, calculée é partir de la dernière relation, donne:

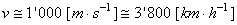  (6)

soit environ 55% d'erreur par rapport à la vraie valeur de 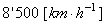 (ce qui est normal avec toutes les hypothèses simplificatrices que nous avons faites...).

La valeur théorique de l'altitude atteinte, même si son expression est très simple à déterminer, est tellement fausse que cela ne vaut pas la peine d'en faire mention.

Les navettes ne vont donc pas à la vitesse de libération avec qu'un seul étage de propulsion et même.... elles n'ont souvent comme seul objectif d'aller seulement à la vitesse de mise en orbite basse... La navette n'est pas libérée de l'attraction terrestre, loin de là!