News :: Erreur :: Statistiques :: ClearType :: Imprimer ::

GÉNIE MARIN & MÉTÉO | GÉNIE MÉCANIQUE | GÉNIE ÉLECTRIQUE
GÉNIE ÉNERGÉTIQUE | GÉNIE CIVIL | GÉNIE BIOLOGIQUE | GÉNIE AÉRONAUTIQUE
GÉNIE SPATIAL | GÉNIE CHIMIQUE | GÉNIE INDUSTRIEL

LISTE DES SUJETS TRAITÉS SUR CETTE PAGE

Le Génie Civil représente l'ensemble des techniques concernant les constructions civiles et les outils qui y sont associés. Les ingénieurs civils s'occupent eux de la conception, de la réalisation, de l'exploitation et de la réhabilitation d'ouvrages de construction et d'infrastructures urbaines dont ils assurent la gestion afin de répondre aux besoins de la société, tout en assurant la sécurité du public et la protection de l'environnement en théorie. Très variées et intéressantes, leurs réalisations se répartissent principalement dans cinq grands domaines d'intervention: structures, géotechnique, hydraulique, transport, et environnement.

Signalons qu'en génie civil il est parfois fait usage du calcul des surfaces minimales. Ceci est déjà traité par un exemple dans le chapitre de Mécanique Analytique.

POULIES

Dans le cadre de la statique des forces il y a un exemple industriel qui est fameux et que nous croisons quasiment toutes les semaines en marchant ou en roulant devant des chantiers (grues), des gares (tendeurs), des ports (bateaux) ou en allant dans des salles de fitness ou garages: la poulie! Son origine est une idée d'Archimède (paraît-il...) qui l'appliqua pour le déplacement de grosses masses nécessaires dans divers chantiers de son époque. La relation avec le génie civil est donc toute justifiée! Voyons donc cela de plus près (exceptionnellement il y a très peu d'équations).

Considérons la situation suivante appelée "poulie simple fixe" avec une masse de 10 [Kg] (soit une force de 100 [N] avec la gravité terrestre arrondie à la dizaine la plus proche) accrochée une corde glissée dans la gouttière d'une poulie:

  (1) Source: Wikipedia

Une poulie simple fixe n'a l'avantage mécanique que de pouvoir exercer la force dans une direction différente à celle du déplacement, la force qui doit être appliquée est la même que celle qui est requise pour déplacer l'objet sans la poulie!

Le point d'ancrage de la poulie doit lui supporter la force nécessaire au déplacement de l'objet plus la force de traction, soit environ deux fois cette force au pire. Sinon le charge totale que doit support le point d'ancrage est fonction de l'angle de tire du cordage (compris entre 90° et 180°) bien évidemment:

  (2)

Pour un angle de 180° le coefficient de charge est de 200%. Une charge de 10 [Kg] sur le cordage représente une charge de 20 [Kg] sur la poulie.

  (3)

Pour un angle de 90°, le coefficient de charge est de 140%. Une charge de 10 [Kg] représente une charge de 14 [Kg] sur la poulie.

Considérons maintenant une situation où nous fixons une extrémité de la corde au support et de tirer avec l'autre extrémité, pour déplacer à la fois la poulie et la charge de 10 [Kg]. Cette configuration est appelée "poulie simple mobile" ou "poulie inversée" (la légende veut dit que c'est ce système qu'Archimède utilisa pour tirer un bateau):

  (4) Source: Wikipedia

Au fait dans ce système (mis en place à la verticale ou à l'horizontale peu importe!) c'est comme s'il y avait deux individus qui se partageaient l'effort du déplacement: le mur et la partie libre de la corde (celle qui est tirée).

La poulie simple mobile permet donc de réduire la force nécessaire au déplacement de moitié (le point d'ancrage supportant l'autre moitié) et en rajoutant ainsi des poulies mobiles, nous continuons à diviser l'action à exercer! C'est bête mais il fallait y penser!

Ce système par contre nécessite un déplacement de l'extrémité de corde tirée du double de la distance du déplacement de la charge et ce indépendamment du rayon de la poulie.

Indiquons aussi que plus la poulie à un rayon grand, plus le moment de force le sera lui aussi! Donc dans le cas de très lourdes charges nous privilégierons des grands rayons pour les poulies si le système qui tire ne peut fournir qu'une faible force.

Une configuration plus réaliste (car nous allons rarement nous placer au-dessus du point d'ancrage pour tirer la corde et en plus le système précédent est peu stable mécaniquement parlant...) de la poulie libre présentée ci-dessus est la suivante:

  (5) Source: Wikipedia

Évidemment quand nous représentons des systèmes comme ceux-ci dans les cas scolaires, nous négligeons de manière simplificatrice la masse des poulies elles-mêmes qu'il faudrait en toute rigueur prendre en compte!

Quand nous utilisons des systèmes de plusieurs poulies qui travaillent ensemble, nous disons que nous avons une configuration de "poulies composées". La configuration de ce type la plus commune est le "palan": les poulies sont distribuées en deux groupes (ou moufle), l'un fixe, l'autre mobile:

  (6) Source: Wikipedia

Dans chaque groupe nous installons un nombre arbitraire de poulies qui démultiplient donc d'un même facteur la charge initiale. La charge est bien évidemment unie au groupe mobile.

Nous avons donc 25 [N] au bout de la corde. Le lecteur peut donc chercher à s'amuser à trouver les 4 points d'accroches dans l'illustration précédente et les deux poulies qui divisent chacune par deux la force nécessaire... Si jamais voici la même configuration mais représentée sous une formé "dépliée":

  (7) Source: Wikipedia

Nous voyons déjà que la grosse poulie supérieure ne sert à rien excepté à changer la direction de la force de tirage. Au fait, les deux poulies qui servent à diviser chacune la force par deux sont les deux inférieures, le reste n'étant là que par commodité pour le mouvement de la corde.

Voyons une application connue des poulies dans certaines gares ferroviaires:

  (8)

Il s'agit d'un palan pour tendre les câbles électriques avec un contrepoids non visible sur la photographie (en bas à droite) qui assure une certaine force donc une certaine tension. L'avantage de ce système est qu'il permet de rajouter des poids au fur et à mesure que le câble se détend et ceux-ci sont alors quatre fois plus élevée au niveau du câble électrique grâce aux deux poulies mobiles (à gauche). Les poulies à droite ne sont là que par commodité pour le mouvement de la corde et la direction de tirage en ce qui concerne la poulie à l'extrémité droite.

Dans le cas d'un levage horizontal ou vertical il est facile de déterminer le rapport de démultiplication D. Effectivement, si nous considérons F la force nécessaire pour soulever l'objet d'une hauteur h en tirant la corde sur une longueur d et 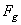 la force de gravitation sur la masse tirée, nous avons alors en négligeant les frottements et le poids des poulies mobiles:

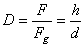  (9)

Enfin, remarquons qu'il est possible de jouer avec le rayon de la poulie de déviation pour diminuer la force à fournir tout en gardant constant le moment de force (nous parlons alors de "palan différentiel") mais au final l'énergie dépensée restera toujours la même pour soulever un objet à une même hauteur (et il faudra tirer la corde encore plus pour soulever la charge à la même hauteur).

SPIRALE DE CORNU

La clothoïde est une courbe transcendante plane dont la courbure est proportionnelle à l'abscisse curviligne.Elle est également appelée "spirale de Cornu", en référence à Alfred Cornu, le physicien français qui l'a inventée. Plus rarement, elle peut apparaître sous le nom de radioïde aux arcs, spirale d'Euler ou spirale de Fresnel.

Cette forme est également adaptée aux fins de courbes dans les tracés des chemins de fer parce qu'un véhicule suivant ce tracé à une vitesse constante subit une accélération angulaire constante, ce qui réduit à la fois les efforts sur les rails et l'inconfort des passagers dans les voitures.

Enfin, les sabots montés sur les pylones de téléphériques, et qui supportent le cable porteur, adoptent cette forme. De fait, il est possible de faire circuler la cabine à sa vitesse maximale sur le pylone, sans incommoder les passagers.

De même cette courbe est utilisée pour les boucles verticales ou loopings dans les montagnes russes pour le confort des passagers, afin que l'accélération verticale subie soit continue

 
  (10)

Lorsqu'un véhicule aborde une courbe circulaire,, il va subir une forme  perpendiculaire à sa direction (force centrifuge) donc de norme (cf. chapitre de Mécanique Classique):

  (11)

dès le début de son entrée dans la courbe. Cet effet est problématique car pour une voiture de poids moyen sur une autoroute, la force centrifuge peut égaler la force de pesanteur (lorsque sa vitesse est dans les valeurs légales!).

Ainsi, l'accélération passe brutalement de 0 à  aussi, les ingénieurs relèvent les courbes pour améliorer l'adhérence, mais il est aussi possible d'essayer de trouver des courbes pour lesquelles l'accélération sera plus progressive. Par exemple si la courbure C donnée par (cf. chapitre de Géométrie Différentielle):

  (12)

est proportionnelle au trajet s (abscisse curviligne) parcouru dans la courbe, nous aurons au début de la courbe  donc l'accélération sera nulle

Ce que nous cherchons est alors des courbes telles que :

  (13)

Pour cela, rappelons que nous pouvons aussi écrire naturellement pour un cercle, la courbure sous la forme:

  (14)

Effectivement, si nous tournons d'un angle  alors nous nous déplaçons d'une longueur  (cf. chapitre de Trigonométrie).

Nous avons donc la relation:

  (15)

Soit:

  (16)

d'où:

  (17)

De plus rappelons que l'équation paramétrique du cercle est:

  (18)

Nous avons donc:

  (19)

Soit:

  (20)

Nous pouvons donc maintenant écrire:

  (21)

Soit:

  (22)

avec un petit changement de variables:

  (23)

il vient:

  (24)

en prenant  (nous pouvons toujours faire une translation par la suite).

Les deux intégrales s'appelent des "intégrales de Fresnel" et ne sont pas calculable directement. Nous pouvons cependant les exprimer sous forme de développement de Taylor sous la forme:

  (25)

Le plot de l'intégral de Fresnel donne dans Maple:

plot([FresnelC(t),FresnelS(t),t=-5..5]);

  (26)

En zoomant sur la partie qui nous intéresse:

  (27)

La même chose à une constante facteur près en utilisant la série de Taylor présentée antérieurement:

  (28)

Les bureaux d'ingénieur utilisent des logiciels spéciaux intégrant des spirales des clothoïdes dans des environnements 2D ou 3D sur la base de relevé topographiques fait par des géomaticiens.

CÂBLES SUSPENDUS

Galilée, fut sans doute le premier à s'intéresser à la chaînette qu'il prit pour un arc de parabole. Jean Bernoulli, Huygens et Leibniz trouvèrent (indépendamment) en réponse au défi lancé par Jakob Bernoulli, sa véritable nature en 1691 : engendrée par un cosinus hyperbolique.

  (29) Source: Chronomaths

Considérons (source: ChronoMath) pour l'étude un câble homogène, flexible, attaché en deux points A et B. Dans sa position d'équilibre, le câble pend dans un plan vertical et semble prendre une forme parabolique. En fait, pas vraiment...

  (30)

Créons dans ce plan un repère orthonormé , où O désigne le point le plus bas du câble et notons  le champ de pesanteur à son endroit.

Appelons  la tension au point O faisant échec à la tension en M de sorte que la portion de câble [OM] de longueur L, soumise à son poids linéique au point G, soit en équilibre au sens statique:

  (31)

Projetons sur les axes de coordonnées en notant  l'angle .

Nous avons alors les décompositions suivantes:

  (32)

Nous pouvons alors écrire le système:

  (33)

Soit après simplification:

  (34)

Soit:

  (35)

En calculant le rapport:

  (36)

Pour obtenir une équation différentielle différentions... (là c'est subtil...):

  (37)

Ensuite:

  (38)

Mais la tangente c'est aussi la dérivée de la fonction décrivant la chaînette. Donc:

  (39)

Il vient alors:

  (40)

Posons  et cherchons la primitive du membre de gauche dans un premier temps (celle du membre droite étant évidente). Les calculs faits dans le chapitre de Calcul Différentiel Et Intégral dans la détermination des primitives usuelles nous donne:

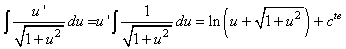  (41)

Nous avons donc:

  (42)

en passant à l'exponentielle:

  (43)

en remarquant que dans notre problème en  nous avons bien.

Pour trouver y' nous utilisons une astuce: Nous savons que la fonction est symétrique. Donc si nous remplaçons x par -x la tangente change aussi de signe et passe de y' a -y':

  (44)

En soustrayant:

 et   (45)

il vient:

  (46)

Donc après intégration:

  (47)

Soit:

  (48)

Nous voyons bien avec Maple la différence entre une parabole et la chainette:

> plot([x^2,cosh(x)],x=-4...4);

  (49)

Considérons maintenant deux points dans le plan ,  et déterminons l'équation de la chaînette de longueur L ayant ces deux points comme extrémités.

Nous avons les deux équations :

  (50)

Nous obtenons une troisième équation à l'aide de la longueur L qui est connue. En effet  (cf. chapitre de Mécanique Analytique):

  (51)

où nous avons toujours:

  (52)

Ainsi nous obtenons un système non linéaire de trois équations à trois inconnues ():

  (53)

Déterminons à titre d'exemple la chaînette de longueur 38 cm passant par les points, .

Il faut alors résoudre le système suivant :

  (54)

Voici les commandes Maple qui nous permettent d'obtenir le résultat.

e1:=0=k*cosh(-9/k+c1)+c2;
e2:=10=k*cosh(9/k+c1)+c2;
e3:=38=k*(sinh(9/k+c1)-sinh(-9/k+c1));
fsolve({e1,e2,e3},{k,c1,c2},{k=0..infinity});
Maple donne : k = 4.073758798, c1 = .2694982504, c2 = -14.46356329.

Graphiquement nous avons alors:

  (55)

Dans le cas des lignes de chemins de fer électrifiées, nous pallions à la flèche (cf. chapitre de Génie Mécanique) rédhibitoire par un câble porteur principal de la caténaire : le câble supérieur (ci-dessous à droite) subit une flèche acceptée, ce qui diminue les tensions entre les pylônes. La caténaire reste ainsi bien linéaire grâce aux accroches auxiliaires multiples à un câble auxiliaire.

  (56) Source Chronomaths

Sinon signalons que nous retrouvons aussi les chaînettes dans tous les endroits de la vie de tous les jours où un câble est suspendu entre deux points sur une même horizontale.

BARRAGES

Considérons le barrage de hauteur z, de longueur L et stockant de l'eau de densité  ci-dessous:

  (57)

Nous avons vu dans le chapitre de Mécanique des Milieux Continus que la pression hydrostatique était donnée par:

  (58)

mais dans cette situation nous avons évidemment:

  (59)

Ainsi lorsque nous nous plaçons à la surface de l'eau en :

  (60)

soit la pression de l'air à la surface du lac de barrage.

Sur un élément de surface d'aire dS il s'exerce une force élémentaire:

  (61)

Or:

  (62)

Ainsi:

  (63)

d'où après intégration

  (64)

Il s'agit donc de la force exercée sur la face immergée. La force sur la face émergée (à gauche sur l'illustration) est simplement donnée en posant . Nous avons donc:

  (65)