|

GÉNIE MARIN &
MÉTÉO | GÉNIE MÉCANIQUE | GÉNIE
ÉLECTRIQUE
GÉNIE ÉNERGÉTIQUE| GÉNIE CIVIL | GÉNIE
BIOLOGIQUE | GÉNIE AÉRONAUTIQUE
GÉNIE SPATIAL | GÉNIE CHIMIQUE | GÉNIE
INDUSTRIEL
Dernière
mise-à-jour de ce chapitre:
09.03.2010 13:58
Version: 1.1 Revision 1
 LISTE DES SUJETS TRAITÉS SUR CETTE PAGE
LISTE DES SUJETS TRAITÉS SUR CETTE PAGE
Nous allons voir dans ce chapitre l'étude
des circuits, montages, puces, et machines, émetteur/récepteurs
que l'ingénieur
doit savoir formaliser, analyser, comprendre, fabriquer et simuler à la
suite de ses études. Pour cette raison, nous avons choisi
sur ce site de nous concentrer sur des cas pratiques en donnant
des exemples d'application dans la vie de tous les jours. Ensuite
le formalisme mathématique
sous forme classique ou complexe sera donné avec éventuellement
les pièges
et dangers du montage.
Nous traiterons ici dans l'électronique analogique, ensuite de
l'électronique de puissance (électrotechnique), de l'électronique
numérique ainsi de que la physique des semi-conducteurs pour bien
comprendre les fondements de certains éléments.
Le génie électrique est donc un hiéarchie de modèles. C'est la
seule façon d'aborder la conception de systèmes complexes. En principe,
le fonctionnement de nombreux dispositifs peut certes toujours
se ramener à l'application des équations de Maxwell (cf.
chapitre d'Electrodynamique), mais cependant humainement impossible de comprendre
la conception de certains systèmes en ce cantonnant à un niveau
aussi théorique.
Il est alors d'usage dans l'industrie de hiérarchiser l'analyse
en 5 niveaux:
N0. Physique du solide: Ce modèle est essentiel pour l'analyse
des propriétés électriques et magnétiques de la matière. Il s'appuie
sur les lois de la physique quantique et mène essentiellement à
la description de bandes d'énergie et au calcul de leur degré d'occupation.
Ce modèle explique par exemple les propriétés fondamentales des
semi-conducteurs.
N1. Électromagnétisme: Ce modèle est essentiel poru l'analyse
des dispositifs travaillant aux hyperfréquences et celle des dispositifs
électromagnétiques. Il s'appuie sur les relations de Maxwell et
fait appel à la théorie mathématique des équations aux dérivées
partielles. Ce modèle ne permet plus d'analyse l'influence d'un
atome car les objets étudiés sont à un niveau plus macroscopique,
décrits pas leurs dimensions, leur permittivité, leur conductabilité,
etc...
N2. Théorie des circuits: Ce modèle est essentiel pour l'analyse
des dispositifs électroniques dans le cas très courant où les dimensions
du dispositifs sont largement inférieurs à la longueur d'oone du
phénomène étudié. Ce modèle s'appuie sur les lemmes de Kirchhoff
et la définition d'une demi-douzaine d'éléments discrets, résistance,
capacité, inductance, cours, etc... Il n'y a plus de géométrique
dans un tel modèle mais seulement une topologie. On peut calculer
le courant et la tension, grandeurs scalaires, alors que les champs
n'ont plus de sens. Les techniques mathématiques sont celles des
équations différentielles ordinaires, transformations de Laplace,
calcul complexe et matriciel, etc...
N3. Schémas fonctionnels: A ce niveau, nous ne tenons plus compte
de courants ou de tensions, in a fortiori de la géométrique du
système. Celui-ci est constitué par la connexion de blocs remplissant
des fonctions caractérisées par des relations entre grandeurs de
sortie et d'entrée.
N4. Systèmes: A ce niveau, nous schématisons en bloc fonctionnel
un ensemble de blocs du niveau 3. Un ordiateurs est par exemple
une interconnexion de différents systèmes logiques réalisant chacun
une fonction particulière.
N5. Logiciel: A partir de ce niveau, l'ingénieur n'ajoute plus
de dispositifs supplémentaires, ne les combine plus en des systèmes
plus vastes, mail il programme la machine. Les méthodes théoriques
se rapprochent alors plus souvent de la linguistique que de la
mathématique.
COURANT ALTERNATIF VS COURANT CONTINU
Le lecteur va remarquer que tout au long de ce chapitre du site,
nous allons principalement travailler avec du courant alternatif.
Il nous semble important d'expliquer l'origine de cet attrait du
monde industriel contemporain pour le courant alternatif avant
d'aller plus loin.
Au fait, l'origine de cet attrait est relativement simple:
Quand des centrales électriques virent le jour, surtout dans
les régions éloignées des centres urbains il fallut transporter
l'énergie électrique produit sur des longues distances. Mais les
câbles qui transportent l'électricité ont une certaine résistance
et cela posa un problème majeur.
Effectivement, une ville moyenne peut largement avoir besoin
d'une puissance d'environ 10 [MW]. Si cette quantité devait être
transportée sous une tension modeste d'environ 100 [V],
comme 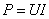 (cf.
chapitre d'Électrocinétique), le courant devait être énorme: 100'000
[A] ! (cf.
chapitre d'Électrocinétique), le courant devait être énorme: 100'000
[A] !
Mais l'effet Joule dans le cuivre de 1 [cm] de diamètre
a une résistance linéaire de 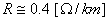 .
Avec un courant de 100'000 [A], la perte d'énergie par effet
Joule serait d'environ (en négligeant la chute de potentiel): .
Avec un courant de 100'000 [A], la perte d'énergie par effet
Joule serait d'environ (en négligeant la chute de potentiel):
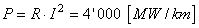 (1)
(1)
... on voit très vite le problème!
Au prix de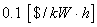 ,
cela représentant un coût (perte) d'environ: ,
cela représentant un coût (perte) d'environ:
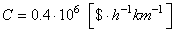 (2)
(2)
humm.....!
Il n'y avait d'autre choix économique que de baisser le courant.
En clair, si la tension atteignait 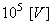 ,
la même puissance pourrait être transportée efficacement par 100
[A]. Ainsi, en élevant la tension par un facteur 1000, nous
pouvons réduire le courant d'un facteur 1000 aussi, et donc la
perte Joule par un facteur ,
la même puissance pourrait être transportée efficacement par 100
[A]. Ainsi, en élevant la tension par un facteur 1000, nous
pouvons réduire le courant d'un facteur 1000 aussi, et donc la
perte Joule par un facteur 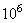 . .
Comme il existait déjà un dispositif simple pour élever et abaisser
la tension alternative (les transformateurs) sans aucun dispositif
comparable pour la tension continue (du moins à l'époque), la course
a été gagnée par les adeptes du courant alternatif.
Il faut rajouter également comme deuxième intérêt que certains
composants électriques linéaires (voir plus loin) n'ont pas pas
beaucoup d'intérêt en courant continu... nous y reviendrons!
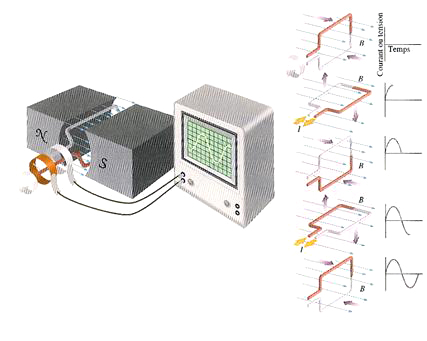
Voyons un montage simple pour générer du courant alternatif monophasé:
(3)
La tension (respectivement le courant) est déterminée par la
loi de Faraday démontrée dans le chapitre d'Electrocinétique:
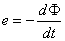 (4)
(4)
qui donne donc la force électromotrice (ou tension dans le cas
d'un générateur sans résistance...) induite.
Nous avons bien évidemment dans la situation ci-dessus si l'aimant
est permanent et la longueur de la spire carrée est L :
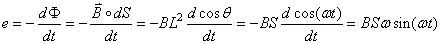 (5)
(5)
Nous voyons déjà que pour obtenir une certaine force électromotrice
il sera préférable de jouer avec la fréquence de rotation plutôt
qu'avec la surface ou l'intensité du champ magnétique... ou encore
d'augmenter le nombre de spires par un montage permettant d'arriver à la
relation suivants:
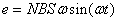 (6)
(6)
Il convient d'indiquer pour les sceptiques qu'il y a bien conservation
de l'énergie dans ce système! Effectivement, l'énergie nécessaire à faire
tourner la spire sera celle en partie utilisée par le système (et
c'est pourquoi les barrages font tourner des turbines avec de l'eau
et les centrales nucléaires avec de la vapeur et les éoliennes
avec du vent...).
Evidemment le cas inverse comme un courant alternatif injecté dans
la spire la fera tourner dans le champ magnétique. Donc dans une
situation nous avons un générateur électrique et dans le cas inverse
un moteur électrique.
Il est possible avec un appareillage similaire de produit une
tension continue à peu près fiable de la manière suivante appelée "dynamo":
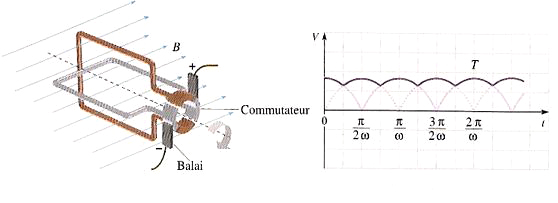
(7)
Le générateur simple donné en premier avec quelques aimants en
fer à cheval produisant le champ magnétique était très utilisé au
début de l'ère de la technologie électrique mais à des tensions élevées (plusieurs
[kV]) et des courants internes élevés aussi (plus de 50
[A]). Les balais métalliques et les bagues collectrices
produisaient alors des étincelles et s'abîmaient relativement vite.
Actuellement, cette machine à armature tournante n'est plus très
utilisée.
Pour éviter les difficultés associées aux tensions dépassant
environ 600 [V], nous faisons aujourd'hui tourner des électroaimants
autour d'une armature immobile. Le courant qui alimente les électroaimants
tournants (qui peuvent aussi être des aiments permanents), est
relativement faible et il ne pose aucun problème
au fonctionnement des bagues et balais. Cette configuration est
appelée alors un "alternateur" (l'exemple
le plus commun étant
la vieille lampe à vélo abusivement appelée dynamo alors que ce
n'est pas une!).
Avec des composants linéaires électriques il est aussi possible
au besoin de redresser la tension (nous verrons cela beaucoup plus
loin). Nous avons alors une dynamo!
CIRCUITS LINÉAIRES EN RÉGIME CONSTANT
Nous allons voir ici des circuits composés d'éléments simples
comme une résistance, une capacité et une impédance. Ces circuits,
dont l'équation représentative est une équation différentielle
linéaire sont appelés "circuits linéaires". Par ailleurs,
ils sont un excellent exemple pour voir la lourdeur des développements
en utilisant des représentations mathématiques classiques à l'opposé d'une
autre technique beaucoup plus souple et puissante.
CIRCUIT RC SÉRIE
Tout circuit possédant un condensateur possède également une
résistance, ne serait-ce que celle des fils de connexion. De tels
circuits RC série sont très courants et parfois d'une grande importance
(stimulateur cardiaque par exemple). Effectivement, quand nous
fermons un circuit qui ne contient que des résistances (circuit
purement résistif), le courant monte à sa valeur nominale dans
un temps extrêmement bref, de sorte que nous pouvons considérer
que le courant et la tension sont constants avec une excelle approximation.
Ainsi, la régime permanent s'établit après un régime transitoire
très bref. Au contraire, dans un circuit RC série, tension et courant
prennent un certain temps pour atteindre leurs valeurs nominales.
Cette dépendance en fonction du temps a de multiples applications
et permet de produire toute une gamme de signaux modulables dans
le temps en fonction des besoins.

(8)
Nous supposons qu'initialement le condensateur est chargé et
qu'il ne circule aucun courant (interrupteur ouvert):
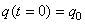 et et 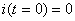 (9)
(9)
Quand nous fermons l'interrupteur les électrons partent du condensateur
C. Nous avons alors aux bornes de la résistance:
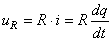 (10)
(10)
aux bornes du condensateur:
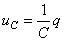 (11)
(11)
L'équation du circuit est alors:
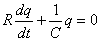 (12)
(12)
Soit:
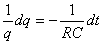 (13)
(13)
Equation différentielle triviale dont la solution est avec les
conditions initiales:
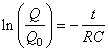 (14)
(14)
Soit:
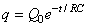 (15)
(15)
Le courant a alors la forme suivant:
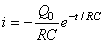 (16)
(16)
Il s'agit donc d'un système où le courant décroît exponentiellement
et ce d'autant plus vite que le facteur RC appelé "constante
de temps" est petit. Nous voyons ce genre de système lorsque
la lumière à l'intérieur d'une voiture s'éteint document après
fermeture des portes.
Lorsque l'on met ce régime sous une tension permanente 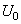 ,
nous avons alors une équation de la forme: ,
nous avons alors une équation de la forme:
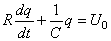 (17)
(17)
Une solution particulière évidente est alors:
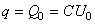 (18)
(18)
Nous avons alors la solution générale:
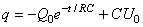 (19)
(19)
soit pour le courant:
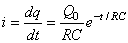 (20)
(20)
Et pour la tension aux bornes du condensateur:
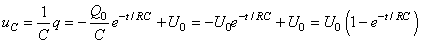 (21)
(21)
ce qui représente donc la tension aux bornes du condensateur
lors de la charge.
Ainsi, en posant 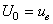 nous
avons respectivement à la fermeture et ouverture du circuit: nous
avons respectivement à la fermeture et ouverture du circuit:

(22)
Etudions maintenant l'aspect énergétique qui est important en
ingénierie puisque la consommation ou perte de puissance (rendement)
est un facteur de vente important dans certaines applications!
Pour cela reprenons la relation:
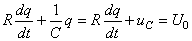 (23)
(23)
et multiplions par i:
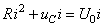 (24)
(24)
Ce que nous écrivons:
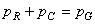 (25)
(25)
Puisque:
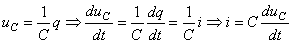 (26)
(26)
où nous voyons donc que dès que le régime transitoire de charge
ou décharge est terminé, la tension aux bornes du condensateur étant
nulle alors le courant est nul.
Nous avons alors:
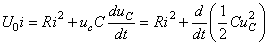 (27)
(27)
où le premier terme est la puissance fournie par le générateur
au circuit, le second est le terme d'effet Joule et le troisième
est la puissance stockée dans le condensateur:
L'énergie fournie par le générateur se retrouve stockée dans
le condensateur et dissipée par la résistance par effet Joule.
Ce qui est le plus important c'est de faire un bilan sur toute
la durée de charge du condensateur pour signaler la puissance dissipée
dans les caractéristique de vente (cela passe mieux que de mettre
des équations...). Pour cela il suffit d'intégrer la relation précédente
de 0 à l'infini pour obtenir l'énergie dissipée.
Le premier terme à gauche de l'égalité donne:
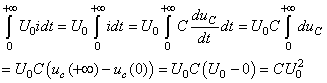 (28)
(28)
Le second terme s'intègre en utilisant i(t):
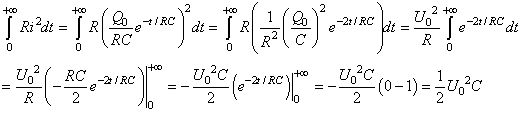 (29)
(29)
Le troisième terme s'intègre immédiatement puisque nous avons
déjà la primitive:
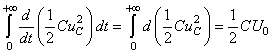 (30)
(30)
Nous obtenons finalement:
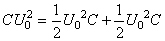 (31)
(31)
Ainsi, pour des durées grandes, la moitié de l'énergie fournie
par le générateur est dissipée par effet Joule et l'autre stockée
dans le condensateur.
CIRCUIT RL SÉRIE
Considérons le circuit suivant:

(32)
Quand nous fermons l'interrupteur nous avons alors aux bornes
de la résistance:
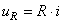 (33)
(33)
et aux bornes de l'inductance:
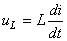 (34)
(34)
et 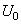 aux
bornes du générateur de tension continue. aux
bornes du générateur de tension continue.
L'équation du circuit est alors:
 (35)
(35)
Soit:
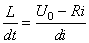 (36)
(36)
En inversant:
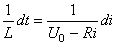 (37)
(37)
Faisons un changement de variable:
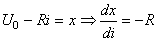 (38)
(38)
Alors:
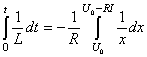 (39)
(39)
Il vient alors après intégration:
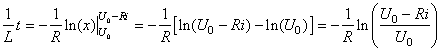 (40)
(40)
Multiplions les deux membres par -R, puis prenons l'exponentielle
des deux membres:
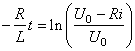 (41)
(41)
et:
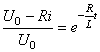 (42)
(42)
Alors:
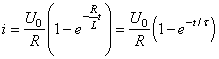 (43)
(43)
où nous avons la constante de temps définie par:
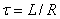 (44)
(44)
Ainsi, à la fermeture de l'interrupteur, la courant croît de
manière exponentielle avec une asymptote à la valeur 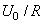 .
Donc contrairement à au circuit RC, le courant tend vers une valeur
fixe non nulle lorsque t tend vers l'infini!!! .
Donc contrairement à au circuit RC, le courant tend vers une valeur
fixe non nulle lorsque t tend vers l'infini!!!
Nous avons donc:
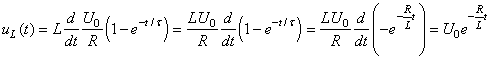 (45)
(45)
Etudions maintenant l'aspect énergétique qui est important en
ingénierie puisque la consommation ou perte de puissance (rendement)
est un facteur de vente important dans certaines applications!
Comme pour le circuit RC, nous allons directement faire un bilan
sur toute la durée du régime transitoire pour signaler la puissance
dissipée dans les caractéristiques de vente (cela passe mieux que
de mettre des équations...)
 (46)
(46)
Multiplions les termes de l'équation différentielle par i(t):
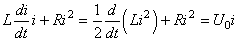 (47)
(47)
Ce que nous écrivons:
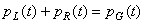 (48)
(48)
Pour calculer l'énergie dissipée, nous procédons de la même manière
que pour le circuit RC série. Nous avons après intégration:
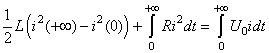 (49)
(49)
soit:
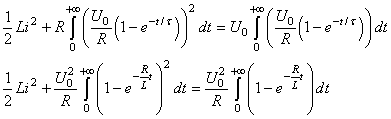 (50)
(50)
Contrairement au cas du circuit RC, nous ne pouvons intégrer
ci-dessus avec les bornes données à cause du "1-" qui
est devant l'exponentielle car celui-ci fait tendre la puissance
consommée vers l'infini ce qui est logique, contrairement au circuit
RC qui finit lui par se bloquer une fois la capacité chargée (le
courant i tendant vers zéro très vite).
Donc soit, nous intégrons seulement jusqu'à un t temps
limite suffisamment grand par rapport aux valeurs des éléments
passifs (deux ou trois 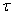 ),
soit nous nous intéressons à titre purement indicatif à la valeur
instantanée de la puissance. Nous avons alors: ),
soit nous nous intéressons à titre purement indicatif à la valeur
instantanée de la puissance. Nous avons alors:
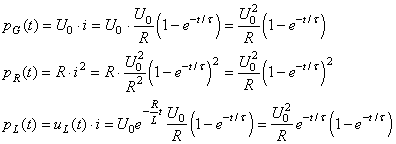 (51)
(51)
Et donc à la fin du régime transitoire quand 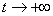 : :
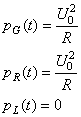 (52)
(52)
donc en régime stable la résistance est le seul élément dissipatif
d'énergie dans le circuit et il suffit de multiplier alors la puissance
dissipée par l'intervalle
de temps désirée pour avoir une estimation de l'énergie dissipée.
CIRCUIT RLC SÉRIE
Un fil électrique (une antenne par exemple) n'est pas un conducteur
parfait. En réalité il peut être assimilé à une résistance, une
capacité et une inductance interne en série. Si prenons le cas
par exemple des générateurs, souvent on ne considère que la résistance
interne comme non négligeable et celle-ci fait bien évidemment
diminuer la tension nominale du générateur d'un facteur en première
approximation proportionnel au courant qui le traverse.
Pour étudier le comportement d'un tel élément souvent appelé "circuit
RLC" nous le représentons d'abord sous la forme suivante:

(53)
Nous supposons qu'initialement le condensateur est chargé et
qu'il ne circule aucun courant (interrupteur ouvert):
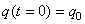 et et 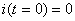 (54)
(54)
Quand nous fermons l'interrupteur les électrons partent du condensateur C.
Nous avons alors aux bornes de la résistance:
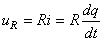 (55)
(55)
aux bornes du condensateur:
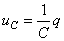 (56)
(56)
aux bornes de la bobine:
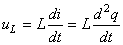 (57)
(57)
La somme des différences de potentiel du circuit est égale à la
différence de potentiel initiale d'où:
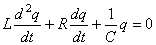 (58)
(58)
ou autrement écrit:
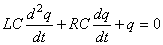 (59)
(59)
Il s'agit d'une équation différentielle linéaire du second ordre.
Pour la résoudre il faut chercher les racines de l'équation caractéristique
associée (cf. chapitre de Calcul Différentiel et Intégral):
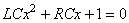 (60)
(60)
Celle-ci a pour discriminant:
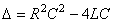 (61)
(61)
La valeur de la résistance pour laquelle ce discriminant est
nul est appelée "résistance critique":
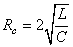 (62)
(62)
Nous pouvons ceci dit écrire le discriminant sous la forme suivante:
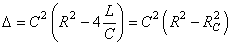 (63)
(63)
Les solutions de l'équation différentielle sont différentes selon
le nombre et le type des racines de l'équation caractéristique.
RÉGIME CRITIQUE
Il s'agit du cas où 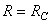 .
L'équation caractéristique admet alors une racine double réelle
puisque: .
L'équation caractéristique admet alors une racine double réelle
puisque:
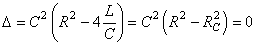 (64)
(64)
Nous avons alors:
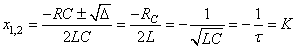 (65)
(65)
avec:
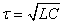 (66)
(66)
L'équation différentielle admet alors une solution du type suivant
lorsque le discriminant est nul (cf. chapitre
de Calcul Différentiel
et Intégral):
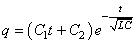 (67)
(67)
en omettant le retard.
Ce qui donne pour l'intensité:
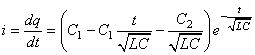 (68)
(68)
Les constantes sont définies par les conditions initiales:
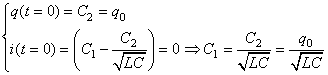 (69)
(69)
Nous obtenons donc pour la solution globale:
(70)
Les figures suivantes illustrent l'allure de l'évolution temporelle
de la charge du condensateur et de l'intensité au travers de l'inductance.
L'intensité est maximale pour 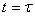 : :

(71)
RÉGIME APÉRIODIQUE (OU HYPERCRITIQUE)
Il s'agit du cas où 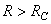 .
L'équation caractéristique admet alors deux racines réelles distinctes: .
L'équation caractéristique admet alors deux racines réelles distinctes:
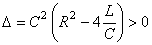 (72)
(72)
Soit:
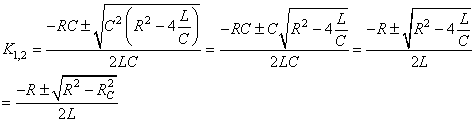 (73)
(73)
Les deux racines sont de même signe car en utilisant les relations
de Viète (cf. chapitre de Calcul Algébrique) nous avons:
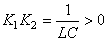 (74)
(74)
Les deux racines sont donc obligatoirement négatives. Nous notons
leurs valeurs absolues:
Ces deux racines sont donc négatives. Nous notons leurs valeurs
absolues :
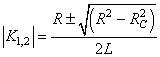 (75)
(75)
qui vérifie donc:
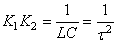 (76)
(76)
Nous avons vu dans le chapitre de Calcul Différentiel Et Intégral
qu'à ce moment la solution (sans déphasage) est de la forme:
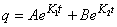 (77)
(77)
Ce qui donne pour l'intensité:
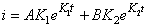 (78)
(78)
Les constantes A et B sont définies par les conditions
initiales:
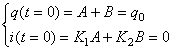 (79)
(79)
Ce qui nous donne:
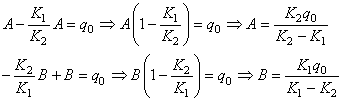 (80)
(80)
Soit sous forme conventionnelle:
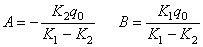 (81)
(81)
Soit en reportant dans les expressions de la charge et de l'intensité:
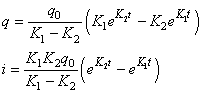 (82)
(82)
Les figures suivantes illustrent l'évolution temporelle de ces
fonctions (se rappeler que les racines sont négatives!).
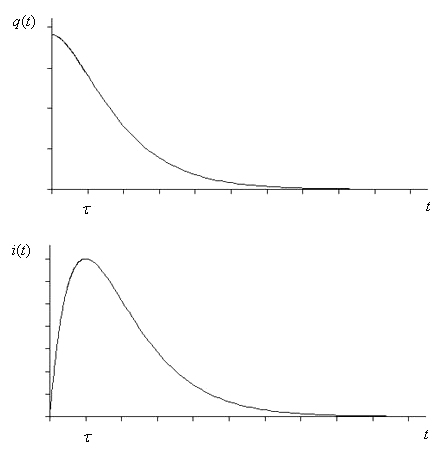
(83)
RÉGIME PSEUDO-PÉRIODIQUE (OU DES OSCILLATIONS AMORTIES)
Il s'agit du cas où 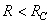 .
L'équation caractéristique admet alors deux racines complexes conjuguées: .
L'équation caractéristique admet alors deux racines complexes conjuguées:
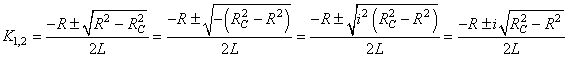 (84)
(84)
qui sont assimilées à la résistance du circuit. Nous l'appelons "impédance
complexe".
Nous allons voir que contrairement à l'intuition de l'époque,
les racines complexes ont une signification physique réelle.
Notons pour cela 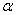 et et 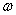 les
valeurs absolues des parties réelle et imaginaires de ces racines: les
valeurs absolues des parties réelle et imaginaires de ces racines:
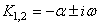 (85)
(85)
avec:
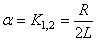 (86)
(86)
et:
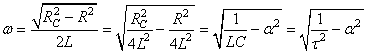 (87)
(87)
Nous avons vu dans le chapitre de Calcul Différentiel et Intégral
que la solution de l'équation différentielle s'écrit alors:
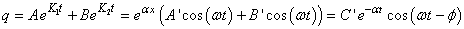 (88)
(88)
Ce qui nous donne pour l'intensité:
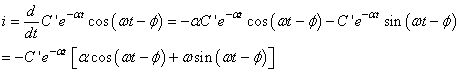 (89)
(89)
Les constantes C' et 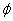 sont
déterminées par les conditions initiales: sont
déterminées par les conditions initiales:
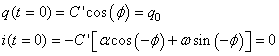 (90)
(90)
Ce qui nous donne:
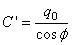 et et 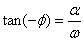 (91)
(91)
Soit:
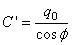 et et 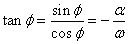 (92)
(92)
Soit en reportant dans les expressions de la charge q et
du courant i:
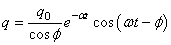 (93)
(93)
et:
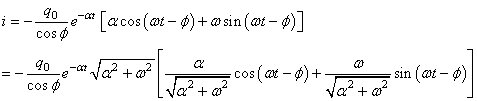 (94)
(94)
D'abord nous avons:
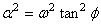 (95)
(95)
d'où:
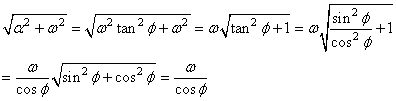 (96)
(96)
Ce qui nous donne:
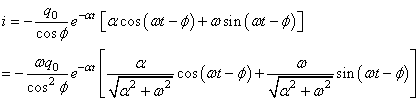 (97)
(97)
Or, nous avons:
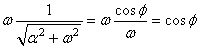 (98)
(98)
et:
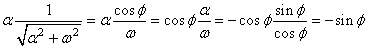 (99)
(99)
Nous avons alors:
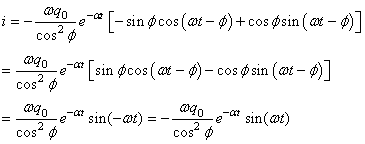 (100)
(100)

(101)
où:
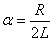 (102)
(102)
est le "facteur d'amortissement". Si nous voulons avoir
de belles oscillations peu amorties, il y a intérêt à avoir ce
terme le plus petit possible donc une valeur de R petite.
Lorsque R est nul nous avons alors:
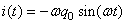 (103)
(103)
avec donc:
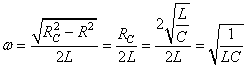 (104)
(104)
Soit une période de:
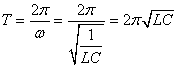 (105)
(105)
Il faut donc jouer alors avec C ou L pour obtenir
la période désirée dans le cas où la résistance est nulle. Signalons également
que cette situation particulière est appelée "oscillateur
harmonique".
Enfin, de par les résultats obtenus nous avons donc la généralisation
des circuits RC, RL ou LC série.
Maintenant, supposons que dans le circuit nous posions une alimentation
continue en série dans le circuit. Nous avons alors:
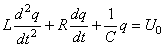 (106)
(106)
L'équation différentielle linéaire à coefficients constants à maintenant
un seconde membre (constant dans ce cas). Nous trouvons alors immédiatement
une solution particulière qu'il suffit ensuite d'ajouter à toutes
les solutions que nous avons obtenues précédemment.
Une solution particulière est donc:
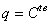 (107)
(107)
Donc:
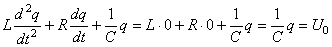 (108)
(108)
Soit:
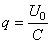 (109)
(109)
Cette solution particulière qui est à ajouter aux solutions précédentes,
n'a aucune influence sur les équations du courant (sa dérivée étant
nulle). Par contre, elle décale sur les graphiques le tracé de q(t)
vers le haut. Voilà donc l'effet qu'il y a à rajouter une source
de tension constante (comme une simple pile par exemple).
CIRCUITS LINÉAIRES EN RÉGIME FORCÉ
L'objectif sera pour commencer, d'étudier le comportement d'un
circuit linéaire
RLC série excité par un générateur de tension sinusoïdale puisqu'il
est une généralisation des circuits RL ou RC (il suffit d'annuler
L ou C respectivement pour tomber sur les solutions d'un circuit
RC ou RL).
Nous avons alors:
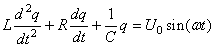 (110)
(110)
Nous pourrions très bien rajouter un déphasage au terme sinus à droite
de l'égalité (arbitraire de phase). Cela ne changerait rien aux
développements qui vont suivre et rappelons aussi que le cosinus
n'est qu'un sinus avec un déphasage bien précis!
Enfin, le plus important, c'est que si nous trouvons une solution
particulière à l'E.D. ci-dessus, alors puisque l'amplitude et la
pulsation peuvent prendre n'importe quelle valeur à un déphasage
arbitraire près alors nous avons donc une infinité de solutions
particulières. Et comme nous avons démontré lors de notre étude
des équations différentielles que la somme de solutions particulières
est aussi solution alors cela signifie qu'une excitation obtenu
avec une série de Fourier aura aussi une solution et en passant à la
limite nous avons une transformée de Fourier!
Donc passons à notre étude. Pour cela, dérivons cette relation
par rapport à t:
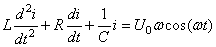 (111)
(111)
Cherchons alors une solution particulière de la forme:
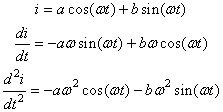 (112)
(112)
Nous remarquons que cette proposition de solution est en tout
point identique à la fondamentale d'une série de Fourier dont le
terme 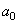 est
nul (qui est la moyenne du signal ou la composante continue si
elle existe)! est
nul (qui est la moyenne du signal ou la composante continue si
elle existe)!
Puis injectons ces relations dans:
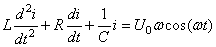 (113)
(113)
en regroupant les termes trigonométriques de même nature:
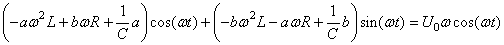 (114)
(114)
Ce qui est équivalent à:
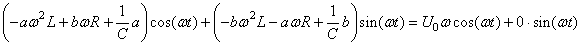 (115)
(115)
d'où en identifiant les termes:
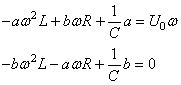 (116)
(116)
Nous pouvons factoriser:
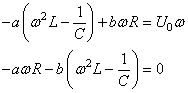 (117)
(117)
Et en simplifiant par 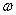 : :
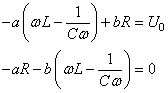 (118)
(118)
et en changeant de signe la deuxième ligne:
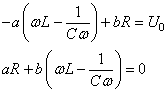 (119)
(119)
Il s'agit donc d'un système de deux équations à deux inconnues a, b que
nous résolvons en posant:
(120)
Ce qui nous donne immédiatement:
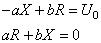 (121)
(121)
d'où:
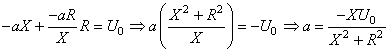 (122)
(122)
et donc:
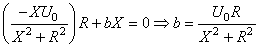 (123)
(123)
Nous posons de plus traditionnellement que:
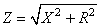 (124)
(124)
Ce qui donne la solution particulière suivante:
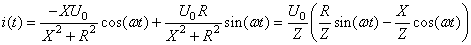 (125)
(125)
à l'arbitraire de phase près.
Il est possible de trouver 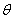 tel
que: tel
que:
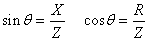 (126)
(126)
Ou autrement écrit (ainsi on voit mieux qu'on balaie toues les
valeurs possibles hors singularités):
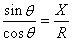 (127)
(127)
Nous avons alors en utilisant les relations trigonométriques
remarquables (cf. chapitre de Trigonométrie):
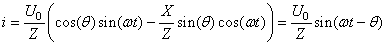 (128)
(128)
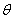 est
donc la phase du courant, soit l'avance ou le retard du courant
sur la tension. Si est
donc la phase du courant, soit l'avance ou le retard du courant
sur la tension. Si 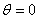 alors
nous avons: alors
nous avons:
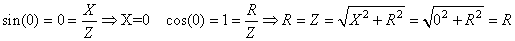 (129)
(129)
et donc:
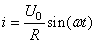 (130)
(130)
nous disons alors qu'il y a résonance du circuit avec donc:
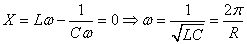 (131)
(131)
FILTRE PASSE-BAS PASSIF
Considérons le cas où L est nul. Nous avons alors:
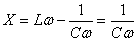 (132)
(132)
Donc:
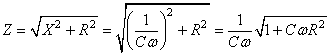 (133)
(133)
D'où:
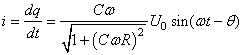 (134)
(134)
Soit:
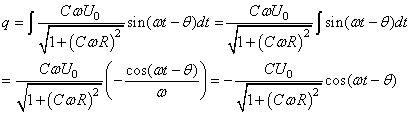 (135)
(135)
Nous avons alors aux bornes du condensateur:
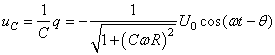 (136)
(136)
Nous voyons donc que la tension aux bornes du condensateur fait
office de ce que nous appelons un "filtre
passe-bas".
C'est-à-dire que l'amplitude de la tension aux bornes du condensateur
par rapport à la tension d'excitation du circuit sera amoindrie
et ce d'autant plus que la fréquence sera grande.
Ce genre d'outil est très pratique pour par exemple éliminer
les harmoniques à haute fréquence d'un signal périodique obtenu
par série de Fourier ou pour nettoyer un bruit à haute fréquence.
On peut également utiliser des filtres passe-bas en cascade afin
de réaliser des analyseurs de spectre.
Voici le tracé du facteur:
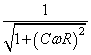 (137)
(137)

Nous voyons bien qu'aux basses fréquences (à gauche) l'amplitude
est conservée (le filtre passe-bas laisse donc passer les basses
fréquences). Au-delà le signal est coupé.
Le rapport:
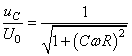 (138)
(138)
est souvent exprimé en décibels soit par définition en utilisant
la mesure:
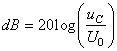 (139)
(139)
et porte alors le nom de "fonction
de transfert" du
filtre.
FILTRE PASSE-HAUT PASSIF
Pour ce qui est de la tension aux bornes de la résistance, nous
avons:
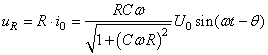 (140)
(140)
ce qui est traditionnellement remanié sous la forme suivante:
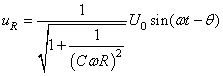 (141)
(141)
Nous voyons donc que la tension aux bornes de la résistance fait
office de ce que nous appelons un "filtre
passe-haut".
C'est-à-dire que l'amplitude de la tension aux bornes de la résistance
par rapport à la tension d'excitation du circuit sera amoindrie
et ce d'autant plus que la fréquence sera faible.
Voici le tracé du facteur:
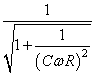 (142)
(142)

Nous voyons bien qu'aux basses fréquences (à droite) l'amplitude
est conservée (le filtre passe-haut laisse donc passer les
hautes fréquences). Au-delà le signal est coupé.
Le rapport:
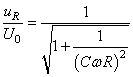 (143)
(143)
est souvent exprimé en décibels soit par définition en utilisant
la mesure:
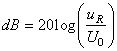 (144)
(144)
et porte alors aussi le nom de "fonction
de transfert" du
filtre.
Avec différents types de filtres assemblés nous pouvons ainsi
supprimer (mais jamais complètement) des plages de fréquences.
Nous parlons alors de filtre coupe-bandes. C'est la technique utilisé par
exemple pour la réception d'une certaine radio ou chaîne de télévision
se trouvant dans une plage de fréquence bien précise. Ou encore
en musique électronique pour atténuer sons graves ou aigus. Ou
encore pour séparer le signal ADSL ou Voix d'une ligne téléphonique.
Un filtre passif se caractérise DONC par l'usage exclusif de
composants passifs linéaires (résistances, condensateurs,
bobines couplées
ou non). Par conséquent, leur gain (rapport de puissance entre
la sortie et l'entrée) ne peut excéder l'unité. Ils ne peuvent
donc qu'atténuer en partie des signaux, mais pas les amplifier
car cela nécessiterait un apport d'énergie (ce qui est le rôle
des "filtres actifs").
INTÉGRATEUR ET DÉRIVATEUR
Nous avons donc aux bornes du condensateur:
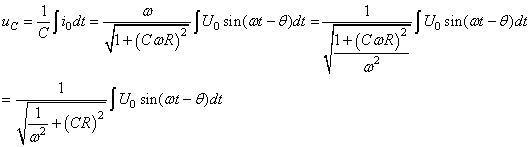 (145)
(145)
Maintenant, si 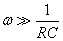 ,
nous avons: ,
nous avons:
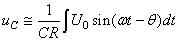 (146)
(146)
Si nous faisons en sorte que 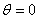 nous
devons avoir: nous
devons avoir:
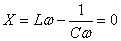 (147)
(147)
Soit:
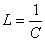 (148)
(148)
Dès lors:
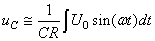 (149)
(149)
Le circuit est alors ce que nous appelons assez logiquement...
un "intégrateur".
Regardons maintenant du côté de la résistance:
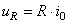 (150)
(150)
Or, nous avons:
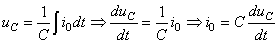 (151)
(151)
Donc:
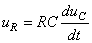 (152)
(152)
Comme:
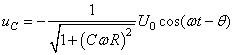 (153)
(153)
Nous avons alors:
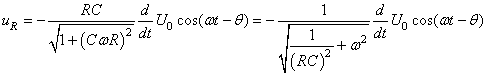 (154)
(154)
Si 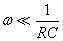 alors: alors:
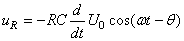 (155)
(155)
Si nous nous arrangeons pour avoir:
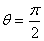 (156)
(156)
alors:
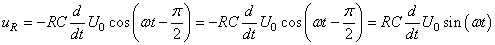 (157)
(157)
Le circuit est alors ce que nous appelons assez logiquement....
un "dérivateur".
L'utilité d'un circuit intégrateur est par exemple de transformer
un signal périodique en une constante (puisque la moyenne temporelle
d'un signal périodique ayant un offset ne sera jamais nulle).
|