|

GÉNIE MARIN & MÉTÉO | GÉNIE
MÉCANIQUE | GÉNIE ÉLECTRIQUE
GÉNIE ÉNERGÉTIQUE| GÉNIE
CIVIL | GÉNIE BIOLOGIQUE | GÉNIE AÉRONAUTIQUE
GÉNIE SPATIAL | GÉNIE
CHIMIQUE | GÉNIE INDUSTRIEL
Dernière
mise-à-jour de ce chapitre:
08.08.2010 20:15
Version: 1.3 Revision 9 | Rédacteur: Vincent Isoz | Avancement: ~60%
 LISTE
DES SUJETS TRAITÉS SUR CETTE PAGE LISTE
DES SUJETS TRAITÉS SUR CETTE PAGE
Le génie industriel englobe la conception, l'amélioration
et l'installation
de systèmes. Il utilise les connaissances provenant des sciences mathématiques,
physiques et sociales, ainsi que les principes et méthodes propres à l'art
de l'ingénieur, dans le but de spécifier, prédire et évaluer
les résultats découlant de ces systèmes.
Nous pouvons résumer tous les domaines qui touchent au génie
industriel (et pas seulement.... cela peut s'appliquer avec adaptation ad hoc
à l'administration) par l'objectif d'optimiser et contrôler
les performances globales de l'entreprise (coûts, délais, qualité)
car:
On ne peut améliorer que ce que l'on mesure!
Remarquons que certaines techniques de génie industriel ont déjà été abordées
dans d'autres chapitres comme les techniques de gestion quantitatives, l'optimisation
(recherche opérationelle), l'analyse financière, l'analyse des
files d'attentes, et autres...
Danc ce chapitre nous traiterons uniquement des deux aspects du SQC (Statistical
Quality Control) soit du contrôle statistique de la qualité (dont
c'est le métier du "qualiticien") dans
le cadre de la fabrication et de la mise en production de biens ou de services.
Selon l'utilisation nous distinguons trois domaines principaux qui dans l'ordre
conventionnel sont:
1. Contrôle statistique de processus, surveillance de fabrication ou
réglage de qualité (Statistical
Process Control, SPC). Il s'agit de la surveillance d'un processus de fabrication
pendant la production de produits de masse, pour découvrir des différences
de qualité et pour pouvoir intervenir et conduire directement.
2. Contrôle de réception ou examen d'échantillon de réception
(Acceptance Sampling, AC). Il s'agit du contrôle d'entrée, d'un
contrôle pendant la production et d'un contrôle final des
produits dans une entreprise (ou usine) sans influence directe sur la production.
Ainsi le montant
de rebut produit est mesuré. Le contrôle initial sert aussi à refuser
la marchandise arrivante. Elle
n'influence par conséquent la production que de manière indirecte.
3. Maintenance préventive et contrôle du veilissement et de la
défaillance et impacts critiques (Analyse des Modes de Défaillances,
de leurs Effets et de leur Criticité, AMDEC). Il s'agit principalement
de calculer la durée de vie de composants ou de machines afin de prévoir
des remplacements à l'avance et les actions y relatives à mener
pour éviter
les situations critiques humaines ou financières.
Indiquons que depuis la fin du 20ème siècle, il est à la
mode de regrouper les deux premiers points dans une méthodologie de
travail appelée "Six Sigma" que nous allons aborder immédiatement.
Enfin, signalons que dans la pratique, pour avoir un intérêt de la direction
d'une entreprise, il faut toujours trouver une relation quantitative entre
non-qualité et les coûts pour pouvoir faire bouger les choses...
SIX SIGMA
Six Sigma est à l'origine une démarche qualité limitée dans un premier temps
aux techniques de "maîtrise statistique des procédés" (M.S.P.)
appelée aussi "statistiques des processus
qualité" (S.P.Q. ou S.P.C. en anglais pour Statistical Process
Control).
C'est une méthodologie de travail utile pour satisfaire
les clients dont l'idée est de délivrer des produits/services
de qualité, sachant que la qualité est inversement
proportionnelle à la variabilité. Par ailleurs, l'introduction
de la qualité doit être optimisée afin de ne pas trop
augmenter les coûts.
Le jeu subtil entre ces deux paramètres (qualité/coûts)
et leur optimisation conjointe est souvent associé au terme de "Lean
management". Si nous y intégrons Six Sigma, nous parlons
alors de "Lean
Six Sigma".
Six Sigma intégre tous
les aspects de la maîtrise de la variabilité en entreprise
que ce soit au niveau de la production, des services, de l'organisation
ou de la gestion
(management). D'où son intérêt! Par ailleurs, dans Six
Sigma un défaut doit
être paradoxalement la bienvenue car c'est une source de progrès
d'un problème
initialement caché. Il faut ensuite se poser plusieurs fois la question "Pourquoi?"
(traditionnellement 5 fois) afin de bien remonter à la source de celui-ci.
Nous distinguons deux types de variablité dans la pratique:
- La "variabilité inhérente" au
processus (et peu modifiable) qui induit la notion de distribution des mesures
(le plus souvent admise par les entreprises comme étant une loi Normale).
- La "variabilité externe" qui
induite le plus souvent un biais (déviation) dans les distributions
dans le temps.
Les processus de fabrication dans l'industrie de pointe ayant une forte tendance à devenir
terriblement complexes, il faut noter que les composants de base utilisés pour
chaque produit ne sont pas toujours de qualité ou de performance égale. Et
si de surcroît, les procédures de fabrication sont difficiles à établir, la
dérive sera inévitablement au rendez-vous.
Que ce soit pour l'une ou l'autre raison, au final bon nombre de produits
seront en dehors de la normale et s'écarteront ainsi de la fourchette correspondant à la
qualité acceptable pour le client. Cette dérive est fort coûteuse pour l'entreprise,
la gestion des rebuts, des retouches ou des retours clients pour non-conformité générant
des coûts conséquents amputant sérieusement les bénéfices espérés.
Comme nous allons le voir dans ce qui suit, une définition possible assez
juste de Six Sigma est: la résolution de problèmes basée sur l'exploitation
de données. C'est donc une méthode scientifique de gestion.
contrôle qualité
Dans le cadre des études qualité en entreprise, nous renonçons souvent à un
contrôle à 100% à cause du prix que cela engendrerait. Nous procédons alors à une
prise d'échantillons. Ceux-ci doivent bien évidemment être représentatifs,
c'est-à-dire quelconques et d'égales chances (in extenso le mélange est bon).
Le but de la prise d'échantillons étant bien évidemment la probabilité du
taux de défaillance réel du lot complet sur la base des défaillances constatées
sur l'échantillonnage.
Rappelons avant d'aller plus loin que nous avons vu dans le chapitre de Statistique
la loi hypergéométrique (et son interprétation) donnée pour rappel par (cf.
chapitre de Statistiques) :
 (1)
(1)
Lors d'un échantillonnage, nous avons normalement un paquet de n éléments
dont nous en tirons p. Au lieu de prendre m (nombre entier!)
comme le nombre d'éléments défectueux nous allons implicitement le définir
comme étant égal à :
 (2)
(2)
où  est
la probabilité (supposée connue ou imposée...) qu'un pièce soit défectueuse.
Ainsi, nous avons pour probabilité de trouver k pièces défectueuses
dans un échantillon de p pièces parmi n : est
la probabilité (supposée connue ou imposée...) qu'un pièce soit défectueuse.
Ainsi, nous avons pour probabilité de trouver k pièces défectueuses
dans un échantillon de p pièces parmi n :
 (3)
(3)
La probabilité cumulée de trouver k pièces défectueuses (entre 0 et k en
d'autres termes) se calcule alors avec la distribution hypergéométrique cumulative
:
 (4)
(4)
 Exemple: Exemple:
Dans un lot n de 100 machines, nous admettons au maximum que 3 soient
défectueuses (soit que  ).
Nous procédons à un échantillonnage p à chaque sortie de commande de
20 machines. ).
Nous procédons à un échantillonnage p à chaque sortie de commande de
20 machines.
Nous voulons savoir dans un premier temps qu'elle est la probabilité que
dans cet échantillonnage p trois machines soient défectueuses et dans
un deuxième temps quel est le nombre de machines défectueuses maximum autorisé dans
cet échantillonnage p qui nous dirait avec 90% de certitude que le lot
de n machines en contienne que de 3 défectueuses.
x |
H(x) |

|
0 |
0.508 |
0.508 |
1 |
0.391 |
0.899 |
2 |
0.094 |
0.993 |
3 |
0.007 |
1.000 |
Tableau: 1
- Application loi hypergéométrique
Ainsi, la probabilité de tirer en une série de tirages trois machines
défectueuses dans l'échantillon de 20 est de 0.7% et le nombre de pièces défectueuses
maximum autorisé dans cet échantillon de 20 qui nous permet avec au moins 90%
de certitude d'avoir 3 défectueuses est de 1 pièce défectueuse trouvée (probabilité cumulée)!
Les valeurs H(x) peuvent être calculées facilement avec MS
Excel. Par exemple la première valeur est obtenue grâce à la fonction LOI.HYPERGEOMETRIQUE(0;20;3;100).
DÉFAUTS/ERREURS
Intéressons-nous donc à exposer pour la culture générale un exemple pratique
et particulier de ce qui n'est qu'une application simple de la théorie des
statistiques et probabilités.
Imaginons une entreprise fabricant trois copies d'un même produit sortant
d'une même chaîne, chaque copie étant composée de huit éléments.
Remarque: Nous
pouvons tout aussi bien imaginer une société de services développant (fabricant)
trois copies d'un logiciel (produit) sortant d'une même équipe de développement
(chaîne), chacun composé d'un nombre égal de modules (éléments).
Supposons que le produit P1 a un défaut, le produit P2 zéro
défauts et le produit P3 deux défauts.
Ici, Six Sigma suppose implicitement que les défauts sont des variables indépendantes
ce qui est relativement rare dans les chaînes de fabrication machines mais
plus courant dans les chaînes dans lesquelles des humains sont les intervenants.
Cependant, nous pouvons considérer lors de l'application SPC sur des
machines qu'un échantillonage
du temps dans le processus de mesure équivaut à avoir une variable
aléatoire!!
Remarques:
R1. Dans le cadre de l'exemple du logiciel pris plus haut, l'indépendance
est peu probable si nous ne prenons pas un exemple dans lequel les modules
sont
personnalisés
selon les besoins du client.
R2. L'inconstance des résultats de production de certaines machines
dont les réglages bougent pendant le fonctionnement... (ce qui est courant),
voir que la matière première change de qualité pendant la production (ce qui
est aussi courant!) posent donc de gros problèmes d'application des méthodes
SPC.
La moyenne arithmétique des défauts nommée dans le standard Six Sigma "Defects
Per Unit" (D.P.U.) est alors défini par :
 (5)
(5)
et donne dans notre exemple :
 (6)
(6)
ce qui signifie en moyenne que chaque produit a un défaut de conception ou
fabrication. Attention! Cette valeur n'est pas une probabilité pour les simples
raisons qu'elle peut d'abord être supérieure à 1 et qu'ensuite elle a comme
dimension des [défauts]/[produits].
De même, l'analyse peut être faite au niveau du nombre total d'éléments défectueux
possibles qui composent le produit tel que nous sommes amenés naturellement à définir
selon le standard Six Sigma le "Defects per Unit
Opportunity" (D.P.O.) :
 (7)
(7)
ainsi, dans notre exemple, nous avons :
 (8)
(8)
et ceci peut être vu comme la probabilité d'avoir un défaut par élément de
produit puisque c'est une valeur sans dimensions :
 (9)
(9)
Par extension nous pouvons argumenter que 87.5% des éléments d'une unité n'ont
pas de défauts et comme Six Sigma aime bien travailler avec des exemples de
l'ordre du million (c'est plus impressionnant) nous avons alors les "Defects
Per Million Opportunities" (D.P.M.O.) qui devient :
 (10)
(10)
ce qui dans notre exemple donne :
 (11)
(11)
Comme la probabilité D qu'un élément d'une pièce
soit non défectueux
est de 87.5% (soit 12.5% de taux de rebus) alors, par l'axiome des probabilités
conjointes (cf.
chapitre de Probabilités), la probabilité qu'un produit
dans son ensemble soit non défectueux est de :
 (12)
(12)
ce qui dans notre exemple donne :
 (13)
(13)
ce qui n'est pas excellent...
Remarque: Dans
Six Sigma, les probabilités conjointes sont aussi naturellement utilisées
pour calculer la probabilité conjointe de produits non défectueux
dans une chaîne
de processus de production P connectés en série. Cette
probabilité conjointe
est appelée dans Six Sigma " Rolled Troughput
Yield" (R.T.Y.) ou " Rendement
Global Combiné" (R.G.C.) et vaut :


(14)
Ce type de calcul étant très utilisé par
les logisticiens qui nomment le résultat "taux
de disponibilité" ainsi que par les chefs de projets pour
la durée d'une phase d'un projet lorsqu'ils considèrent la durées des tâches
comme indépendantes.
Ainsi, dans une chaîne industrielle basée sur l'exemple
précédent
pour avoir une quantité Q bien définie de produits (supposés
utiliser qu'un seul composant de chaque étape) au bout de
la chaîne
il faudra à l'étape A prévoir :
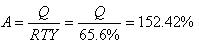 (15)
(15)
soit 52.42% de composants A de plus que prévus. Il
faudra prévoir à l'étape B:
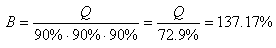 (16)
(16)
soit 37.17% de composants de plus. Et ainsi de suite...
Rappelons maintenant que la densité de probabilité d'avoir k fois
l'événement p et N-k fois l'événement q dans n'importe
quel arrangement (ou ordre) est donné par (cf. chapitre
de Statistiques):
 (17)
(17)
et est appelée la loi binomiale ayant pour espérance et écart-type (cf.
chapitre de Statistiques) :
 (18)
(18)
Ainsi, dans le standard Six Sigma, nous pouvons appliquer la loi binomiale
pour connaître quelle est la probabilité d'avoir zéros éléments
défectueux et 8 autres en bon état de marche sur un produit de
la chaîne de fabrication de notre exemple (si tous les éléments
ont la même
probabilité de tomber en panne...):
 (19)
(19)
et nous retombons bien évidemment sur la valeur obtenue avec les probabilités
conjointes avec :
 (20)
(20)
Ou la probabilité d'avoir un élément défectueux et sept autres en bon état
sur un produit de la chaîne de fabrication :
 (21)
(21)
nous voyons que la loi binomiale nous donne 39.26% de probabilité d'avoir
un élément défectueux sur 8 dans un produit.
Par ailleurs, dans le chapitre de statistiques, nous avons démontré que lorsque
la probabilité p est très faible et tend vers zéro mais que toutefois
la valeur moyenne  tend
vers une valeur fixe si n tend vers l'infini, la loi binomiale de moyenne tend
vers une valeur fixe si n tend vers l'infini, la loi binomiale de moyenne  avec k épreuves était
donnée alors donnée par : avec k épreuves était
donnée alors donnée par :
 (22)
(22)
avec :
 (23)
(23)
Remarque: Dans
un cadre pratique, il est fait usage de l'estimateur de maximum de vraisemblance
de la loi expontentielle pour déterminer la moyenne et l'écart-type
ci-dessus (cf. chapitre de Statistiques).
Ce que Six Sigma note naturellement :
 (24)
(24)
avec :
 (25)
(25)
Ainsi, dans notre exemple, il est intéressant de regarder la valeur obtenue
(qui sera forcément différente étant donné que nous sommes loin d'avoir une
infinité d'échantillons et que p est loin d'être petit) en appliquant
une telle loi continue (la loi continue la plus proche de la loi binomiale
en fait) :
 (26)
(26)
avec :
 (27)
(27)
ce qui est un résultat encore plus mauvais qu'avec la loi binomiale pour
nos produits.
Cependant, si p est fixé au départ, la moyenne  tend également
vers l'infini théoriquement dans la loi de Poissons de plus l'écart-type tend également
vers l'infini théoriquement dans la loi de Poissons de plus l'écart-type  tend également
vers l'infini. tend également
vers l'infini.
Si nous voulons calculer la limite de la distribution binomiale, il s'agira
donc de faire un changement d'origine qui stabilise la moyenne, en 0 par exemple,
et un changement d'unité qui stabilise l'écart, à 1 par exemple. Ce calcul
ayant déjà été fait dans le chapitre de statistique, nous savons que le résultat
est la loi de gauss-laplace :
 (28)
(28)
Ainsi, dans notre exemple, nous avons  et
l'écart-type est donné par l'estimateur sans biais de l'écart-type (cf.
chapitre de Statistique) : et
l'écart-type est donné par l'estimateur sans biais de l'écart-type (cf.
chapitre de Statistique) :
 (29)
(29)
ce qui dans notre exemple donne  . .
Pour calculer la probabilité nous calculons la valeur numérique de la loi
de Gauss-Laplace pour  : :
 (30)
(30)
Ainsi, en appliquant la loi Normale nous avons 24.19% de chance de tirer
au premier coup un produit défectueux. Cet écart par rapport aux autres
méthodes s'expliquant simplement par les hypothèses de départ (nombre d'échantillons
fini, probabilité faible, etc.)
Remarque: Ceux
qui penseraient utiliser la loi triangulaire (cf. chapitres
de Statistiques) doivent tout de suite l'oublier. Effectivement, comme
en qualité la valeur optimiste sera le zéro par définition, la probabilité que
le nombre de défauts soit égal à 0 sera immédiatement de zéro.
INDICES DE CAPABILITÉ
Six Sigma défini plusieurs indices permettant de mesurer pendant le processus
de fabrication la capabilité de contrôle dans le cas d'un grand nombre
de mesures de défauts répartis souvent selon une loi de Gauss-Laplace (loi
Normale).
Basiquement, si nous nous imaginons dans une entreprise, responsable de la
qualité d'usinage d'une nouvelle machine, d'une nouvelle série de pièces, nous
allons être confrontés aux deux situations suivantes:
1. Au début de la production, il peut y avoir de gros écarts de qualité dûs
à des défauts de la machine ou de réglages importants mal initialisés. Ce sont
des défauts qui vont souvent être rapidement corrigés (sur le court terme).
Dès lors pendant cette période de grosses corrections, nous faisons des contrôles
par lot (entre chaque grosse correction) et chacun sera considéré comme une
variable aléatoire indépendante et identiquement distribuée (selon une loi
Normale)
mais de moyenne
et écart-type
bien évidemment différents.
2. Une fois les gros défauts corrigés, nous n'allons avoir en théorie plus
que des défauts minimes très difficilements contrôlables et ce même sur long
terme.
Alors l'analyse
statistique ne se fait plus forcément par lot de pièces mais par pièces et
l'ensemble des
pièces sur le long terme est considéré comme un unique lot à chaque fois.
Ces deux scénarios mettent en évidence que nous n'effectuons
alors logiquement pas les mêmes analyses en début de production
et ensuite sur le long terme. Raison pour laquelle en SPC nous définissons
plusieurs indices (dont les notations sont propre à ce site Internet
car elles changent selon les normes) dont 2 principaux qui sont:
D1. Nous appelons "Capabilité potentielle
du procédé
court terme"
le rapport entre l'étendue de contrôle E de
la distribution des valeurs et la qualité de Six Sigma (6 sigma) lorsque
le processus est centré (c'est-à-dire sous contrôle) tel que :
 (31)
(31)
ce qui s'écrit aussi :
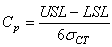 (32)
(32)
où USL est la limite supérieure de contrôle/tolérance ou "Upper
Specification Level" (USL) de la distribution et LSL la limite
inférieure ou "Lower Specification Level" (LSL)
que nous imposons souvent (mais pas toujours!) dans l'industrie comme à distances égales
par rapport à la
moyenne  théorique
souhaitée. théorique
souhaitée.
Ce rapport est utile dans l'industre dans le sens où l'étendue E (qui
est importante car elle représente la dispersion/variation du processus)
est assimilée à la "voix du client" (ses exigences)
et le 6 sigma au dénominateur
au comportement réel du procédé/processus et que la valeur
6 est censée inclure
quasiment toutes les issues possibles. Il vaut donc mieux espérer que
ce rapport soit au pire égal à l'unité!
Voici typiquement un exemple en gestion de projets où lorsque le client
ne paie pas pour une modélisation du risque fine on tombe sur ce type
de distribution (le client accepte que le consultant puisse garantir une variation
qui ne dépassera pas les 50% de l'estimation sans modélisation du risque):

(33)
Remarque: En
MSP, l'étendue E est souvent notée IT, signifiant "intervalle
de tolérance".
L'écart-type au dénominateur étant donné par la relation démontrée dans
le chapitre de Statistique dans le cas de k variables aléatoires
indépendantes et identiquement distribuées selon une loi Normale (mais d'écart-type
et moyenne non-identique):
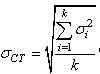 (34)
(34)
où CT est l'abréviation de "court terme" (abréviation
souvent non précisée dans la pratique car supposée connue dans le contexte).
Cet écart-type
est bien évidemment le meilleur pour le premier scénario dont
nous avons fait mention plus haut. Car entre chaque grosse correction, les
lots sont considérés
comme indépendants et ne peuvent pas être analysés comme
un seul et unique lot (ce serait une abérration!).
Attention cependant! Comme souvent dans la situation court terme (lors de
la correction des grosses sources d'erreurs donc) les lots de tests sont petits,
même très petits, afin de diminuer les coûts en production. Dès lors l'écart-type
se trouvant sous la racine (qui est l'estimateur de maximum de vraisemblance
de la loi Normale) n'a pas une valeur vraiment correcte... Il est alors bon
d'utiliser soit d'autres méthodes de calcul assez empiriques comme le font
de nombreux
logiciels, soit de calculer un intervalle de confiance de l'indice de capabilité
en calculant l'intervalle de confiance de l'écart-type court terme comme nous
l'avons vu dans le chapitre de Statistique.
D2. Nous appelons "Performance globale du procédé long
terme" le
rapport entre l'étendue de contrôle E de la distribution des valeurs
et la qualité de Six Sigma (6 sigma) lorsque le
processus est centré tel que :
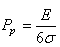 (35)
(35)
ce qui s'écrit aussi :
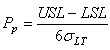 (36)
(36)
L'écart-type au dénominateur étant donné cette
fois par le cas où nous considérons tous les gros défauts
corrigés et le processus
stable afin de considérer toutes les pièces fabriquées comme
un seul et unique lot de contrôle:
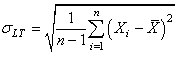 (37)
(37)
où LT est l'abréviation de "long terme" (abréviation
souvent non précisée dans la pratique car supposée connue
dans le contexte).
Cet écart-type est bien évidemment le meilleur pour le deuxième
scénario dont nous avons fait mention plus haut. Car les variations
étant par hypothèses maintenant toutes petites, l'ensemble de la fabrication
peut être supposée comme étant un seul et unique lot de contrôle sur le long
terme (bon cela n'empêche pas qu'il faut parfois nettoyer les valeurs extrêmes
qui peuvent se produire).
Le tolérancement des caractéristiques est donc très important pour l'obtention
de la qualité et de la fiabilité des produits assemblés. Traditionnellement,
une tolérance s'exprime sous la forme d'un bipoint [Min,Max]. Une caractéristique
est alors déclarée conforme si elle se situe dans les tolérances.
Le problème
du tolérancement consiste à tenter de concilier la fixation des limites
de variabilité acceptable les plus larges possibles pour
diminuer les coûts de production et d'assurer un niveau de qualité optimal
sur le produit fini.
Deux approches tentent de résoudre ce problème:
1. Le tolérancement au pire des cas garanti l'assemblage dans toutes les
situations à partir
du moment où les caractéristiques élémentaires sont dans les tolérances.
2. Le tolérancement statistique tient compte de la faible probabilité d'assemblages
d'extrêmes entre eux et permet d'élargir de façon importante les tolérances
pour diminuer les coûts et c'est donc à celui-ci que nous allons nous
intéresser
ici comme vous l'aurez compris.
Un processus est dit "limite capable" (soit
limite stable par rapport aux exigences du client en d'autres termes) s'il
le ratio donné ci-dessus (en choisissant 6 fois l'écart-type)
est supérieur à 1. Mais dans l'industrie on préfère
prendre en réalité la valeur de ~1.33 dans le cas d'une distribution
Normale des données.
Bien évidemment, la valeur  de
l'écart-type peut-être être calculée en utilisant les estimateurs de maximum
de vraisemblance avec ou sans biais vus dans le chapitre de Statistiques mais
il ne s'agit en aucun cas dans la réalité pratique de l'écart-type
théorique mais d'un estimateur. Par ailleurs, nous verrons plus loin
qu'en fonction de l'écart-type utilisé, les notations des indicateurs
changent! de
l'écart-type peut-être être calculée en utilisant les estimateurs de maximum
de vraisemblance avec ou sans biais vus dans le chapitre de Statistiques mais
il ne s'agit en aucun cas dans la réalité pratique de l'écart-type
théorique mais d'un estimateur. Par ailleurs, nous verrons plus loin
qu'en fonction de l'écart-type utilisé, les notations des indicateurs
changent!
Remarque: En
entreprise, il faut faire attention car l'instrument de mesure rajoute son
propre écart-type (erreur) sur celui de la production.
Comme nous l'avons démontré au chapitre de Statistique, l'erreur-type (écart-type
de la moyenne) est :
 (38)
(38)
Dans la méthodologie Six Sigma nous prenons alors souvent pour les processus
à long terme et sous contrôle:
 (39)
(39)
quand nous analysons des cartes de contrôles dont les variables aléatoires
sont des échantillons de n variables aléatoires indépendantes
et identiquement distribuées et que les limites n'ont pas été imposées
par un client ou par une politique interne ou des contraintes techniques! Bien évidemment,
il faut bien être
conscient que UCL et LCL n'ont pas la même expression
dans des cas plus complexes et donc pour des distributions autre que la loi
Normale!
Par ailleurs l'expression précédente diffère aussi pour
les processus à court
terme car l'exemple donnée ci-dessus est pour un cas de mesures sur
le long terme uniquement pour rappel!
Le lecteur remarquera que nous avons maintenant:
 (40)
(40)
Normalement, au sein des entreprise, l'étendue de contrôle est fixe (le numérateur)
et donc quand la valeur de l'écart-type type est grande (plus de variations,
moins de contrôles) la valeur de l'indice est faible et lorsque l'écart-type
est faible (moins de variations, plus de contrôles) la valeur de l'indice est élevé.
Comme le montre les deux exemples ci-dessous :

(41)
L'indice  impose
que la moyenne (l'objectif) est centrée entre LSL et USL. Dès lors, la moyenne
est confondue avec ce que nous appelons la "cible" T du
processus. impose
que la moyenne (l'objectif) est centrée entre LSL et USL. Dès lors, la moyenne
est confondue avec ce que nous appelons la "cible" T du
processus.
Mais la moyenne  dans
la réalité peut être décalée par rapport à l'objectif T initial qui
doit lui toujours (dans l'usage courant) être à distance égale entre USL et
LSL comme le montre la figure ci-dessous dans le cas particulier d'une loi
Normale : dans
la réalité peut être décalée par rapport à l'objectif T initial qui
doit lui toujours (dans l'usage courant) être à distance égale entre USL et
LSL comme le montre la figure ci-dessous dans le cas particulier d'une loi
Normale :

(42)
Mais ce n'est pas forcément le cas dans la réalité où les ingénieurs (quelque
soit leur domaine d'application) peuvent choisir des LSL et USL asymétriques
par rapport à la moyenne ne serait-ce que parce que la loi n'est pas toujours
Normale
(typiquement
le
cas en gestion de projets...)! D'où la définition suivante :
D2. Nous appelons alors "Capabilité
potentielle décentrée court terme du procédé" (dans
le cas décentré) ou "Process
Capability Index (within)" la relation :
 (43)
(43)
avec :
 (44)
(44)
où  est
appelé le "dégré de biais" et T le "target" donné naturellement
par: est
appelé le "dégré de biais" et T le "target" donné naturellement
par:
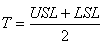 (45)
(45)
qui donne le milieu de la distribution relativement au bi-point [LSL,USL]
imposé (ne pas oublier que l'écart-type au dénominateur
de la relation antéprécédente est l'écart-type
court terme!).
Au fait cet indicateur de capabilité de contrôle peut sembler
très artificiel mais il ne l'est pas totalement.... Effectivement il y a quelques
valeurs remarquables (celles qui intéressent l'ingénieur) qui
permettent de se faire une bonne idée ce qu'il se passe avec celui-ci:
1. Si la moyenne et la cible sont confondues nous avons alors:
 (46)
(46)
nous nous retrouvons donc avec  et
donc et
donc  et
le critère de jugement de la valeur de l'indice sera basée sur l'indice de
capabilité centrée court terme. et
le critère de jugement de la valeur de l'indice sera basée sur l'indice de
capabilité centrée court terme.
2. Si faute d'un mauvais contrôle du processus nous avons :
 (47)
(47)
alors la moyenne  est
soit au-dessus de USL soit en-dessous de LSL ce qui a pour conséquence d'avoir est
soit au-dessus de USL soit en-dessous de LSL ce qui a pour conséquence d'avoir  et
donc et
donc  . .
3. Si nous avons :
 (48)
(48)
alors la moyenne  est
comprise entre les valeurs USL et LSL ce qui a pour conséquence d'avoir est
comprise entre les valeurs USL et LSL ce qui a pour conséquence d'avoir  et
donc et
donc  . .
4. Si nous avons:
 (49)
(49)
alors cela signifie simplement que la moyenne est confondue avec USL ou LSL et nous avons alors  et et  . .
Comme l'interprétation reste cependant délicate et difficile, nous construisons
les indices "Upper
Capability Index CPU" et "Lower Capability
Index CPL" donnés par:
 (50)
(50)
Voyons d'où viennent ces deux valeurs et comment les utiliser:
Démonstration:
D'abord, nous avons besoin de deux formulations particulière du degré de
biais k.
Si:
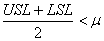 (51)
(51)
alors nous pouvons nous débarrasser de la valeur absolue:
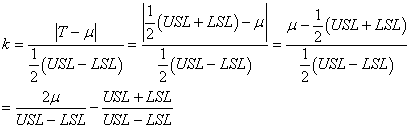 (52)
(52)
Si:
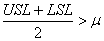 (53)
(53)
alors nous pouvons nous débarrasser de la valeur absolue:
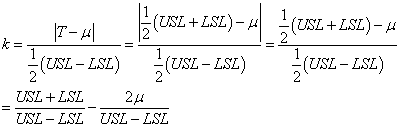 (54)
(54)
Nous avons alors lorsque 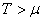 : :
 (55)
(55)
et respectivement lorsque 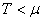 : :
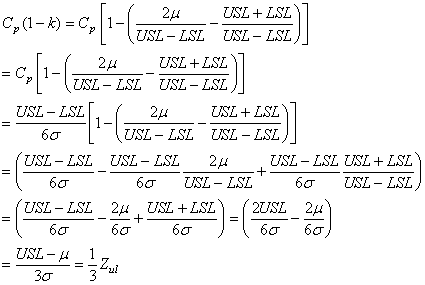 (56)
(56)
 C.Q.F.D. C.Q.F.D.
A long terme dans certaines entreprises il est intéressant de savoir qu'elles
sont les plus mauvaises valeurs prises par les indices CPU et CPL
(c'est le cas dans le domaine de la production mais pas forcément de
la gestion de projets)
Les plus mauvaises valeurs étant trivialement les plus petites, nous prenons
souvent (avec quelques une des notations différentes que l'on peut
trouver dans la littérature spécialisée...):
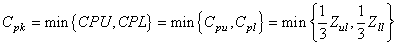 (57)
(57)
Voici par exemple un diagramme d'analyse de la capabilité produit
par le logiciel Minitab (en anglais) avec les différents facteurs susmentionnés
sur un échantillons de 68 données suivant une loi Normale (un
test de normalité a été fait avant):

(58)
Deux lectures typiques sont possibles (nous expliquerons la partie inférieure
gauche du graphique plus loin):
1. En production: Le processus est capable (valeur >1.33) mais avec
une (trop) forte déviation vers le gauche par rapport à la cible
définie
ce qui n'est pas bon (CPL ayant
la
valeur la plus petite) et doit être corrigé.
2. En gestion de projets: Les tâches redondantes sont sous contrôle
(valeur
>1.33) mais avec une forte déviation vers le gauche ce qui peut être
bon si notre objectif est de prende de l'avance par rapport au planifié (rien à corriger).
Il faut vraiment prendre garde au fait que dans la réalité il
n'est pas toujours possible de prendre la loi Normale or tous les exemples
donnés ci-dessus ce sont basés sur cette hypothèse simplificatrice.
Toujours le cadre de la gestion de la qualité en production, la figure
ci-dessous représente bien la réalité dans le cadre d'un processus court ou
long terme:

(59)
Source: MSP/SPC de Maurice Pillet
Chaque petite gaussienne en gris clair, représente une analyse de lots. Effectivement,
nous voyons bien que leurs moyennes ne cessent de bouger pendant la période
de mesures (que cette variation soit grande ou très faible).
Or la relation définissant  supposait,
comme nous l'avons mentionné que le processus est sous contrôle centré (donc
toutes les gaussiennes sont alignées) et sur une optique court-terme. supposait,
comme nous l'avons mentionné que le processus est sous contrôle centré (donc
toutes les gaussiennes sont alignées) et sur une optique court-terme.
De même, la relation définissant 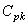 supposait,
comme nous l'avons mentionné que le processus est sous contrôle, sur une optique
court terme et décentré par choix (ou à cause du fait que la loi n'est pas
Normale). supposait,
comme nous l'avons mentionné que le processus est sous contrôle, sur une optique
court terme et décentré par choix (ou à cause du fait que la loi n'est pas
Normale).
Par contre, si le processus n'est pas centré parce qu'il n'est pas sous contrôle
alors qu'il devrait l'être, la variable aléatoire mesurée est la somme
de la variation aléatoire des réglages X de la machine et des variations
aléatoires
non-contrôlables des contraintes des pièces Y.
L'écart-type total est alors, si les deux variables aléatoires suivent une
loi normale, la racine carrée de la somme des écart-types (cf.
chapitre de Statistiques):
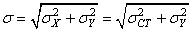 (60)
(60)
Or, si nous n'avons qu'une seule mesure, il vient en prenant l'estimateur
biaisé (c'est un peu n'importe quoi de l'utiliser dans ce cas là mais bon...)
:
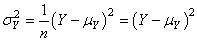 (61)
(61)
Or dans le cas d'étude qui nous intéresse Y représente la moyenne
expérimentale (mesurée) du processus qu'on cherche à mettre sous contrôle.
Cette moyenne est notée traditionnellement m dans le domaine.
Ensuite, 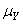 n'étant
pas connu on prend ce qu'il devrait être: c'est la cible T du processus.
Ainsi, nous introduisons un nouvel indice appelé "Capabilité potentielle
décentrée
moyenne court terme du procédé" : n'étant
pas connu on prend ce qu'il devrait être: c'est la cible T du processus.
Ainsi, nous introduisons un nouvel indice appelé "Capabilité potentielle
décentrée
moyenne court terme du procédé" :
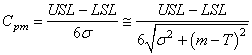 (62)
(62)
où encore une fois il faut se rappeler que l'écart-type dans la racine au
dénominateur est l'écart-type court terme!
Nous voyons immédiatement que plus 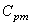 est
proche de est
proche de  mieux
c'est (dans les domaines de production du moins). mieux
c'est (dans les domaines de production du moins).
Nous avons donc finalement les trois indices de capabilités court terme centré et
non centré les plus courants (nous avons délibérément choisi d'uniformiser
les notations et de mettre le maximum d'infos dans celles-ci):
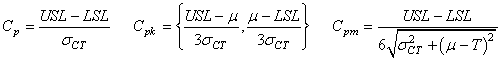 (63)
(63)
De même nous avons aussi les trois indices de capabilités long terme centré et
non centré les plus courants (nous avons délibérément choisi d'uniformiser
les notations et de mettre le maximum d'infos dans celles-ci):
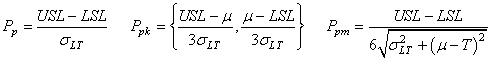 (64)
(64)
Enfin, indiquons que bien que ce soit pas très pertinent, il arrive parfois
que certains ingénieurs fassent les deux analyses (court terme + long terme)
en même temps sur la même base de données de mesures.
Cependant, pour faire de l'analyse objective sur les indices de capabilité vus
jusqu'à maintenant, il faudrait d'abord que les instruments de mesure soient
eux-mêmes capables... ce que nous appelons souvent les "méthodes R&R"
(Répétabilité,
Reproductibilité).
Le principe consiste alors à évaluer la dispersion courte terme ou respectivement
long terme de l'instrument de mesure afin de calculer une "capabilité de
processus de contrôle" définie par:
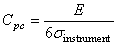 (65)
(65)
Dans les cas classiques, nous déclarons le moyen de contrôle capable pour
une suivi MSP lorsque cette capabilité est supérieure à 4 et nous allons de
suite voir pourquoi. Rappelons pour cela d'abord que:
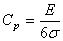 (66)
(66)
Mais la variance observée est au fait la somme de la "vraie" variance
et de celle de l'instrument telle que:
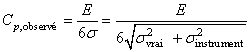 (67)
(67)
Or nous avons:
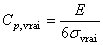 et et 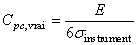 (68)
(68)
En mettant le tout au carré, nous en déduisons:
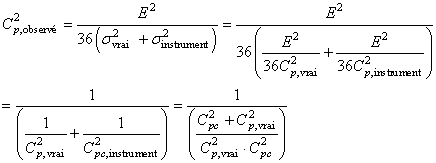 (69)
(69)
D'où:
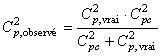 (70)
(70)
Ce qui nous donne:
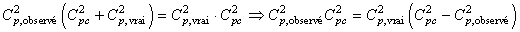 (71)
(71)
Soit:
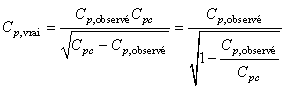 (72)
(72)
Ce qui se traduit par le graphique de la figure suivante qui montre bien
l'intérêt d'un 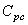 au
moins égal à 4! au
moins égal à 4!

(73)
Dans la pratique, signalons que pour déterminer 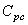 on
se sert d'une pièce étalon mesurée par interférométrie LASER et s'assurer ensuite
que tous les essais répétés de mesure se fassent sur les deux mêmes points
de mesure. on
se sert d'une pièce étalon mesurée par interférométrie LASER et s'assurer ensuite
que tous les essais répétés de mesure se fassent sur les deux mêmes points
de mesure.
Une fois ceci fait, on effectue plusieurs mesures de la cote étalon et on
prend l'écart-type de ces mesures. Ce qui donnera le 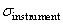 . .
L'étendue E est elle imposée par le client ou par des ingénieurs internes à l'entreprise.
Elle sera souvent prise comme étant au plus dixième de l'unité de tolérance
d'une pièce.
Par exemple, si nous avons un diamètre intérieur de 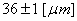 (étendue
de tolérance de 2 microns ce qui est déjà du haut de gamme niveau de précision
car à notre époque le standard se situe plutôt autour des 3!), notre appareil
devra alors avoir selon la règle précédemment citée une étendue de 0.2 microns....
Il est alors aisé de déterminer qu'elle devra être l'écart-type maximum de
l'instrument si on se fixe une capabilité de processus de contrôle de 4 (et
encore... 4 c'est grossier!). (étendue
de tolérance de 2 microns ce qui est déjà du haut de gamme niveau de précision
car à notre époque le standard se situe plutôt autour des 3!), notre appareil
devra alors avoir selon la règle précédemment citée une étendue de 0.2 microns....
Il est alors aisé de déterminer qu'elle devra être l'écart-type maximum de
l'instrument si on se fixe une capabilité de processus de contrôle de 4 (et
encore... 4 c'est grossier!).
Certains ingénieurs apprécient de savoir à combien d'éléments en millions
d'unités produites (parties par million: PPM) seront considérées comme défectueuses
relativement.
Le calcul est alors aisé puisque l'ingénieur a à sa disposition au moins
les informations suivantes:
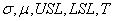 (74)
(74)
et que les données suivent une loi Normale alors il est immédiat que (cf.
chapitre de Statistiques):
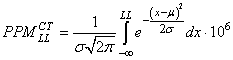 (75)
(75)
et:
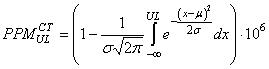 (76)
(76)
valeurs très aisées à obtenir avec n'importe quel tableur comme MS Excel
par exemple.
Nous avons alors
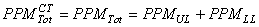 (77)
(77)
il en est de même pour la capabilité long-terme (il suffit de prendre alors
l'expression correspondante de l'écart-type).
NIVEAUX DE QUALITÉS
Signalons un point important relativement à Six Sigma. Au fait, objectivement,
l'idée de cette méthode est certes de faire de la SPC (entre
autres, mais ça
ce n'est pas nouveau) mais surtout de garantir au client selon la tradition
couramment admise avec un écart-type ayant une borne supérieure
de 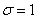 avec
une déviation à la moyenne (en valeur absolue) de 1.5 avec
une déviation à la moyenne (en valeur absolue) de 1.5 par
rapport à la cible ce qui garantit au plus 3.4 PPM (c'est-à-dire 3.4
rejets par million). par
rapport à la cible ce qui garantit au plus 3.4 PPM (c'est-à-dire 3.4
rejets par million).
Remarque: Ce choix empirique vient de la mise
en pratique de la méthode Six Sigma par son créateur (Bill Smith).
Il a observé dans
son entreprise (Motorola) que sous contrôle statistique il avait
quasimment systématiquement une déviation comprise entre 1.2
et 1.8  à
la moyenne pour tous ses procédés industriels.
Voyons d'où vient cette dernière valeur à l'aide des deux tableaux suivants:
1. D'abord construisons un tableau de type idéal qui présente des données
d'un procédé court terme (mais les calculs sont parfaitement identiques pour
du long terme) centré sur la cible (de cible nulle ici, ce qui est un cas typique),
de moyenne nulle (donc sur la cible et alors donc 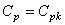 )
et d'écart-type unitaire avec USL et LSL symétriques (ce qui restreint par
contre le champ d'application): )
et d'écart-type unitaire avec USL et LSL symétriques (ce qui restreint par
contre le champ d'application):
Cp |
Cpk |
Défauts (PPM) |
Niveau de qualité Sigma |
Critère |
0.5 |
0.5 |
133614 |
1.5 |
Mauvais |
0.6 |
0.6 |
71861 |
1.8 |
|
0.7 |
0.7 |
35729 |
2.1 |
|
0.8 |
0.8 |
16395 |
2.4 |
|
0.9 |
0.9 |
6934 |
2.7 |
|
1 |
1 |
2700 |
3 |
|
1.1 |
1.1 |
967 |
3.3 |
|
1.2 |
1.2 |
318 |
3.6 |
|
1.3 |
1.3 |
96 |
3.9 |
Limite |
1.4 |
1.4 |
27 |
4.2 |
|
1.5 |
1.5 |
6.8 |
4.5 |
|
1.6 |
1.6 |
1.6 |
4.8 |
|
1.7 |
1.7 |
0.34 |
5.1 |
|
1.8 |
1.8 |
0.067 |
5.4 |
|
1.9 |
1.9 |
0.012 |
5.7 |
|
2 |
2 |
0.002 |
6 |
Excellent |
Tableau: 2
- Capabilité, Niveau de qualité Sigma et P.P.M. dans procédé centré
où tout les données sont obtenues à l'aide des relations suivantes à partir
de l'indice de capabilité potentielle uniquement:
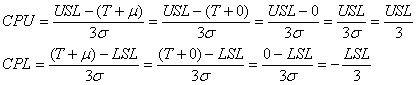 (78)
(78)
si l'écart-type est réduit (ce qui peut toujours être fait et ne change point
la justesse des résultats!). Et puisque dans le tableau ci-dessus LSL et USL sont
symétrique par rapport à la cible:
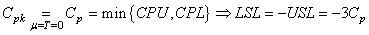 (79)
(79)
et les PPM sont conformément à ce que nous avons vus juste avant donnés par:
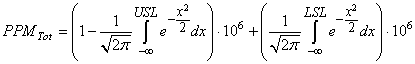 (80)
(80)
et donc puisque dans l'exemple ci-dessus LSL et USL sont symétrique par rapport à la
cible cela se simplifie en:
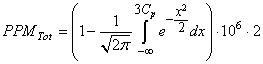 (81)
(81)
où par exemple la valeur du PPM donnée à la ligne "Limite" est obtenue
avec Maple à l'aide de la commande:
>evalf((1-1/sqrt(2*Pi)*int(exp(-x^2/2),x=-infinity..3.9))*2)*1E6;
ou avec MS Excel (version anglais):
=(1-NORMDIST(3.9;0;1;1))*1E6
Il nous reste à voir d'où provient le "niveau
de qualité sigma" noté 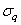 qui
est au fait donné à l'aide du tableau que nous avions construit dans le chapitre
de Statistique: qui
est au fait donné à l'aide du tableau que nous avions construit dans le chapitre
de Statistique:
Niveau
de qualité Sigma |
Taux
de non-défection assuré en % |
Taux
de défection en parties par million |

|
68.26894 |
317'311 |

|
95.4499 |
45'500 |

|
99.73002 |
2'700 |

|
99.99366 |
63.4 |

|
99.999943 |
0.57 |

|
99.9999998 |
0.002 |
Tableau: 3
- Capabilité, Taux de non-défection en % et PPM
et nous avions donné la commande Maple pour obtenir ses valeurs qui sont
toutes valables pour tout écart-type et toute espérance!
2. Maintenant construisons le tableau au pire selon Six Sigma, soit un tableau
en procédé non centré (c'est-à-dire où 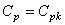 n'est
pas satisfait) avec une déviation
de la moyenne de n'est
pas satisfait) avec une déviation
de la moyenne de 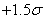 (donc à droite
mais on pourrait prendre à gauche et les résultats seraient les mêmes)
par rapport à la
cible et d'écart-type unitaire avec USL et LSL symétriques (ce
qui restreint toujours le champ d'application): (donc à droite
mais on pourrait prendre à gauche et les résultats seraient les mêmes)
par rapport à la
cible et d'écart-type unitaire avec USL et LSL symétriques (ce
qui restreint toujours le champ d'application):
Cp |
Cpk |
Défauts (PPM) |
Niveau de qualité Sigma |
Critère |
0.5 |
0 |
501350 |
1.5 |
Mauvais |
0.6 |
0.1 |
382572 |
1.8 |
|
0.7 |
0.2 |
27412 |
2.1 |
|
0.8 |
0.3 |
184108 |
2.4 |
|
0.9 |
0.4 |
115083 |
2.7 |
|
1 |
0.5 |
66810 |
3 |
|
1.1 |
0.6 |
35931 |
3.3 |
|
1.2 |
0.7 |
17865 |
3.6 |
|
1.3 |
0.8 |
8198 |
3.9 |
Limite |
1.4 |
0.9 |
3467 |
4.2 |
|
1.5 |
1 |
1350 |
4.5 |
|
1.6 |
1.1 |
483 |
4.8 |
|
1.7 |
1.2 |
159 |
5.1 |
|
1.8 |
1.3 |
48 |
5.4 |
|
1.9 |
1.4 |
13 |
5.7 |
|
2 |
1.5 |
3.4 |
6 |
Excellent |
Tableau: 4
- Capabilité, Niveau de qualité Sigma et P.P.M. dans procédé décentré
où tout les données sont obtenues à l'aide des relations suivantes à partir
de l'indice de capabilité potentielle uniquement:
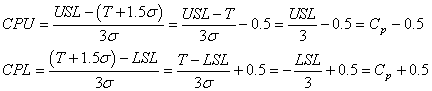 (82)
(82)
et donc:
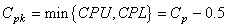 (83)
(83)
d'où:
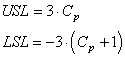 (84)
(84)
et les PPM sont conformément à ce que nous avons vus juste avant donnés par:
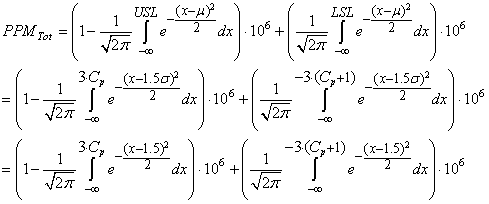 (85)
(85)
où la ligne "Limite" du tableau précédent est par exemple obtenue
avec Maple à l'aide
de la commande:
>evalf((1-1/sqrt(2*Pi)*int(exp(-(x-1.5)^2/2),x=-infinity..(1.3*3))))*1E6+evalf((1/sqrt(2*Pi)*int(exp(-(x-1.5)^2/2),x=-infinity..-(3*(1.3+1)))))*1E6;
ou avec MS Excel:
=(((1-NORMDIST(3*1.3;1.5;1;1))+NORMDIST(-3*(1.3+1);1.5;1;1)))*1E6
On comprend enfin en voyant cette fameuse ligne "Limite" pourquoi
un procédé sous-contrôle est dit "limite capable" avec un indice
de capabilité potentielle de 1.33 étant donné le nombre de PPM!
Donc le but dans la pratique c'est bien évidemment d'être dans la situation
du premier tableau avec pour valeur correspondante dans ce premier tableau à un
niveau de qualité sigma de 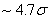 pour
avoir l'équivalent des 3.4 PPM du deuxième tableau (car il est plus facile
de centrer un procédé que de contrôler ses écarts). pour
avoir l'équivalent des 3.4 PPM du deuxième tableau (car il est plus facile
de centrer un procédé que de contrôler ses écarts).
Toute l'importance des valeurs calculées ci-dessous est dans l'application
de procédés de fabrication à n-étapes
en série
(considérés sous la dénomination de "processus"). Cette
application sera présentée dans le chapitre sur les Techniques de Gestion.
 Exemple: Exemple:
Faisons un résumé de tout cela en considérant une nouvelle
petite production de 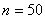 pièces
par lot de 10 (afin d'ajuster en cours de production). La mesure de côtes de
5 pièces chaque heure pendant 10 heures avec une tolérance de pièces
par lot de 10 (afin d'ajuster en cours de production). La mesure de côtes de
5 pièces chaque heure pendant 10 heures avec une tolérance de 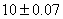 soit
en termes de centièmes un étendue de: soit
en termes de centièmes un étendue de:
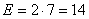 (86)
(86)
et une cible de 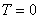 (en
termes d'écarts). Nous avons les données suivantes: (en
termes d'écarts). Nous avons les données suivantes:
| |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
1 |
-2 |
-4 |
-1 |
0 |
4 |
0 |
3 |
0 |
1 |
-1 |
2 |
0 |
-3 |
0 |
-2 |
1 |
-2 |
0 |
1 |
-1 |
2 |
3 |
-1 |
0 |
-3 |
-1 |
0 |
0 |
-1 |
-1 |
3 |
1 |
4 |
1 |
1 |
-2 |
2 |
2 |
0 |
1 |
0 |
4 |
0 |
5 |
-1 |
-1 |
-3 |
0 |
0 |
3 |
3 |
2 |
1 |
0 |

|
-0.6 |
-1.4 |
-1.8 |
-0.2 |
1.4 |
0.2 |
1.2 |
0.4 |
1.6 |
0.5 |

|
1.14 |
2.07 |
1.30 |
1.48 |
1.67 |
1.79 |
1.79 |
1.14 |
1.95 |
1.14 |
Tableau: 5
- Application d'analyse de maîtrise statistique des procédés
Nous voyons immédiatement que le processus de fabrication a été non-stationnaire
pendant cette première production il faudra donc apporter des corrections à l'avenir:

(87)
ou sous forme de carte de contrôle (comme je les aime) avec la représentation
d'un écart-type de 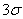 (ce
qui est suffisant pour des petites quantité des pièces bon marché à fabriquer): (ce
qui est suffisant pour des petites quantité des pièces bon marché à fabriquer):

(88)
Donc on devine quand même que le processus est limite....
Remarque: Une chose intéressante c'est que l'on peut analyser aussi ce graphique
en utilisant les outils mathématiques de l'analyse des séries temporelles
(cf. chapitre d'Économétrie).
D'abord, si nous voulons faire une étude statistique pertinente des différentes
données ci-dessus nous pouvons calculer la moyenne générale des écarts qui
sous l'hypothèse d'une distribution Normale est la moyenne arithmétique (cf.
chapitre de Statistiques):
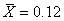 (89)
(89)
Ensuite l'écart-type des données de toutes les pièces est de:
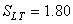 (90)
(90)
en utilisant l'estimateur de maximum de vraisemblance de la variance de la
loi Normale:
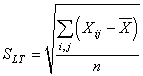 (91)
(91)
nous avons une valeur supérieur à 1 ce qui est donc non-conforme à ce que
Six Sigma exige dans son niveau de qualité.
Donc l'erreur-standard (l'estimateur de l'écart-type de la moyenne) est de:
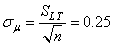 (92)
(92)
Donc l'intervalle de confiance à 95% de la moyenne est de (cf.
chapitre de Statistiques):
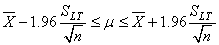 (93)
(93)
Soit dans notre cas:
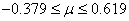 (94)
(94)
Et l'inférence statistique avec notre écart-type long terme utilisant le
test d'hypothèse bilatéral du 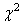 donne
(cf. chapitre de Statistiques): donne
(cf. chapitre de Statistiques):
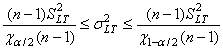 (95)
(95)
Ce qui nous donne dans notre cas:
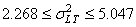 (96)
(96)
soit:
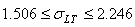 (97)
(97)
Nous remarquons alors que sur une analyse long terme nous avons les intervalles:
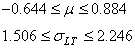 (98)
(98)
Calculons maintenant la performance globale du procédé long terme (si supposé centré donc!).
Nous avons:
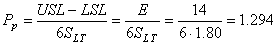 (99)
(99)
Mais avec un instrument ayant un 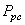 de
4, cela correspond réellement à: de
4, cela correspond réellement à:
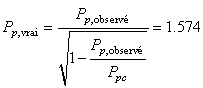 (100)
(100)
De plus, indiquons que comme nous savons faire un calcul d'intervalle de
confiance pour 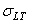 (voir
le calcul fait précédemment), il est alors aisé d'en avoir un pour (voir
le calcul fait précédemment), il est alors aisé d'en avoir un pour 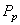 aussi! aussi!
Si l'analyse de la performance globale du procédé long terme est non centrée
(ce qui est le cas ici) nous utilisons donc:
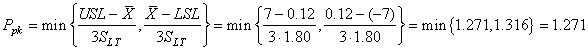 (101)
(101)
et nous savons encore une fois qu'à cause de l'instrument, cette valeur
est un peu sous-évaluée! Nous avons bien évidemment:
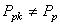 (102)
(102)
donc le processus n'est pas centré (on s'en doutait...). Alors il faut calculer
la capabilité potentielle décentrée moyenne long terme du procédé 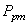 selon
les relations déterminées plus haut: selon
les relations déterminées plus haut:
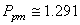 (103)
(103)
Bref, que ce soit de la valeur de 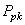 , , 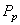 ou ou 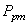 ,
nous voyons que les valeurs sont toutes limites capable (c'est-à-dire
que la valeur est supérieure à 1 - voir définition plus
haut pour un rappel de ce que signifie "limite capable"). ,
nous voyons que les valeurs sont toutes limites capable (c'est-à-dire
que la valeur est supérieure à 1 - voir définition plus
haut pour un rappel de ce que signifie "limite capable").
Si nous faisons alors nos calculs de PPM selon les relations obtenues
plus haut avec la valeur de 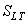 et
de et
de 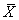 obtenues,
nous avons alors: obtenues,
nous avons alors:
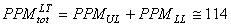 (104)
(104)
Ensuite dire ce chiffre est bon ou mauvais cela est difficile car il nous
manque l'information de savoir quel est le coût de production, le coût de revient
et de réparation d'un produit et le tout est lui-même dépendant de la quantité total
fabriquée! Mais nous pouvons utiliser aussi le modèle de Taguchi pour connaître
la valeur des paramètres (moments) calculés qu'il serait préférable de ne pas
dépasser!
Calculons maintenant les indices de capabilité court terme! Pour cela, il
nous faut l'estimateur de la moyenne de l'ensemble en considérant chaque échantillon
comme une variable aléatoire. Nous savons (cf. chapitre
de Statistiques) que
cette moyenne est aussi la moyenne arithmétique dans le cas d'une loi Normale
et elle est strictement égale à celle que l'on calcule en considérant l'ensemble
des échantillons comme une seule et unique variable aléatoire. Donc il vient
que:
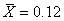 (105)
(105)
En ce qui concerne l'écart-type par contre ce n'est pas pareil. Mais nous
savons (cf. chapitre de Statistiques) que la loi Normal est stable par la somme.
Par exemple, nous avions démontré que étant donné deux variables aléatoires
indépendantes et distribuées selon une loi Normale (en imaginant que chaque
variable représente deux de nos dix échantillons), nous avions donc pour leur
some.:
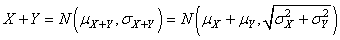 (106)
(106)
Or nous avons aussi démontré dans le chapitre de Statistiques que de par
la propriété de linéarité de l'espérance, nous avons:
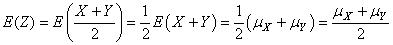 (107)
(107)
ce qui est conforme à notre remarque précédent pour la variance:
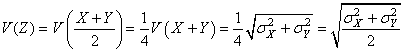 (108)
(108)
Donc in extenso:
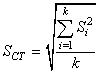 (109)
(109)
et dans notre cas particulier:
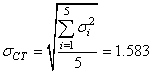 (110)
(110)
nous avons une valeur supérieur à 1 ce qui est donc non-conforme à ce que
Six Sigma exige dans son niveau de qualité.
Donc l'erreur-standard (l'estimateur de l'écart-type de la moyenne) est de:
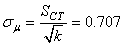 (111)
(111)
Donc l'intervalle de confiance à 95% de la moyenne est de (cf.
chapitre de Statistiques):
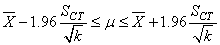 (112)
(112)
Soit dans notre cas:
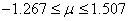 (113)
(113)
Nous remarquons donc qu'en court terme, l'intervalle est beaucoup plus large
qu'en long terme ce qui est normal étant donné la faible valeur de k (qui
vaut donc 5 dans notre exemple).
Et l'inférence statistique avec notre écart-type long terme utilisant le
test d'hypothèse bilatéral du 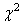 donne
(cf. chapitre de Statistiques): donne
(cf. chapitre de Statistiques):
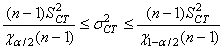 (114)
(114)
Ce qui nous donne dans notre cas:
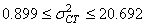 (115)
(115)
soit:
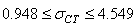 (116)
(116)
Nous remarquons alors que sur une analyse long terme avec les intervalles:
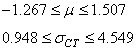 (117)
(117)
Les variations peuvent donc être énormes avec une probabilité cumulée de
95% et il faudra prendre garde dans un cas pratique d'apporter des réglages
au plus vite afin de diminuer aux maximum les moments!
Calculons maintenant la capabilité potentielle du procédé court terme (si
supposé centré donc!). Nous avons:
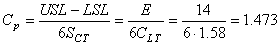 (118)
(118)
Donc nous avons:
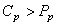 (119)
(119)
ce qui est normal car si les mesures que nous avons étaient vraiment faites
sur une longue période alors ce serait très problématique alors que sur une
courte période c'est déjà un peu plus normal. D'où cette relation d'ordre entre
les deux indices.
Mais avec un instrument ayant un 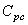 de
4, cela correspond réellement à: de
4, cela correspond réellement à:
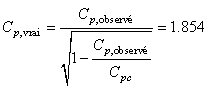 (120)
(120)
De plus, indiquons que comme nous savons faire un calcul d'intervalle de
confiance pour 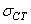 (voir
le calcul fait précédemment), il est alors aisé d'en avoir un pour (voir
le calcul fait précédemment), il est alors aisé d'en avoir un pour 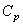 aussi! aussi!
Si l'analyse de la capabilité potentielle du procédé court terme est non
centrée (ce qui est le cas ici) nous utilisons donc:
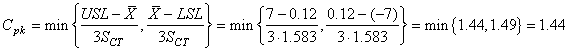 (121)
(121)
et nous savons encore une fois qu'au cause de l'instrument, cette valeur
est un peu sous évaluée! Nous avons bien évidemment:
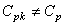 (122)
(122)
donc le processus n'est pas centré (on s'en doutait...). Alors il faut calculer
la capabilité potentielle décentrée moyenne court terme du procédé 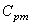 selon
les relations déterminées plus haut: selon
les relations déterminées plus haut:
(123)
Bref, que ce soit de la valeur de 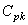 , , 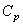 ou ou 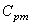 ,
nous voyons que les valeurs sont toutes limites capable. ,
nous voyons que les valeurs sont toutes limites capable.
Si nous faisons alors nos calculs de PPM selon les relations obtenues
plus haut avec la valeur de 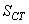 et
de et
de 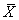 obtenues,
nous avons alors: obtenues,
nous avons alors:
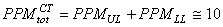 (124)
(124)
Ensuite dire ce chiffre est bon ou mauvais cela est difficile car il nous
manque l'information de savoir quel est le coût de production, le coût de revient
et de réparation d'un produit et le tout est lui-même dépendant de la quantité total
fabriquée! Mais nous pouvons utiliser aussi le modèle de Taguchi pour connaître
la valeur des paramètres (moments) calculés qu'il serait préférable de ne pas
dépasser!
Modèle de Taguchi
Dans le cadre des SPC il est intéressant pour un industriel d'estimer les
pertes financières générées par les écarts à la cible (attention on peut appliquer
également cette approche dans d'autres domaines que l'industrie!)
Nous pouvons avoir une estimation relativement simple et satisfaisante de
ses pertes (coûts) sous les hypothèses suivantes:
H1. Le processus est sous contrôle (écart-type constant) et suit une loi
de densité symétrique décroissante à gauche et à droite par rapport à la cible
(qui peut être une côte, un nombre d'erreurs par périodes, etc.)
H2. Le coût est nul lorsque la production (ou le travail) est centrée sur
la cible (minimum).
H3. Le coût augmente de manière identique lorsque la production se décentre
sur la gauche et sur la droite (ce qui n'est plus le cas dans le domaine de
l'administration par exempl). La fonction de coût
passe donc selon H2 et H3 par un minimum sur la cible.
Dès lors, si nous notons Y le décentrage par rapport à la cible T et L la
perte financière ("loss" en anglais d'où le L). Nous avons:
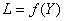 (125)
(125)
Même si nous ne connaissons pas la forme de cette fonction, nous pouvons
l'écrire sous forme de développement de Taylor autour de T tel que (cf.
chapitre de Suites et Séries):
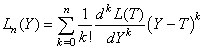 (126)
(126)
Si nous développons au troisième ordre:
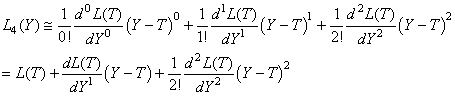 (127)
(127)
Or par l'hypothèse H2, nous avons L(T) qui est nul. Il reste
alors:
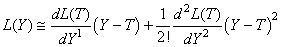 (128)
(128)
et comme par H3, la dérivée de la fonction L(Y) est nulle en T puisqu'il
s'agit d'un minimum alors:
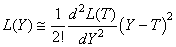 (129)
(129)
Ce qui est noté en SPC:
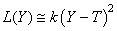 (130)
(130)
et est appelée "fonction de perte de Taguchi" ou
plus simplement "fonction perte de qualité".
Bon c'est bien joli d'avoir cette relation mais comment doit-on l'utiliser?
Au fait, c'est relativement simple. Sous les hypothèses mentionnées plus
haut, si nous avons en production des mesures de défauts (côtes, retards, pannes,
bug, etc.) alors il suffit de calculer leur moyenne arithmétique 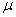 (estimateur
de la moyenne d'une loi Normale) et ensuite de savoir le coût financier ou
horaire L que
cela a engendré pour l'entreprise ou l'institution (parfois cette moyenne est
calculée
sur la base d'un unique échantillon...). (estimateur
de la moyenne d'une loi Normale) et ensuite de savoir le coût financier ou
horaire L que
cela a engendré pour l'entreprise ou l'institution (parfois cette moyenne est
calculée
sur la base d'un unique échantillon...).
Donc la relation précédente devient:
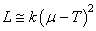 (131)
(131)
avec L et 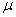 connus. connus.
Et comme T est donné par les exigences du client ou du contexte alors
il est aisé d'obtenir
le facteur k:
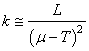 (132)
(132)
qui est au fait mathématiquement parlant
le point d'inflexion de la fonction mathématique L .
Cette dernière relation est parfois notée:
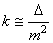 (133)
(133)
Une fois que nous avons k avec une bonne estimation, il est possible
de connaître L pour toute valeur Y et ainsi nous pouvons calculer
en production le coût d'une déviation quelconque par rapport à la cible.
 Exemple: Exemple:
Considérons une alimentation pour une chaîne stéréo pour laquelle T vaut
110 [V]. Si la tension sort des 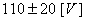 alors
la stéréo tombe en panne et doit être réparée. Supposons que le coût de réparation
est (tous frais directs et indirects compris!) de 100.-. Alors le coût associé pour
une valeur donnée
de la tension est: alors
la stéréo tombe en panne et doit être réparée. Supposons que le coût de réparation
est (tous frais directs et indirects compris!) de 100.-. Alors le coût associé pour
une valeur donnée
de la tension est:
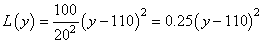 (134)
(134)
Voyons maintenant une manière élégante de calculer le coût moyen de Taguchi
(perte unitaire moyenne). Nous avons bien évidemment dans une chaîne de production
sur plusieurs pièces
d'une même famille:
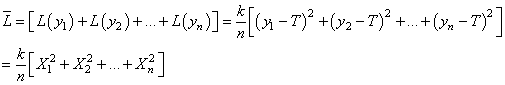 (135)
(135)
où les 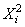 sont
des variables aléatoires normales (gaussiennes par hypothèse). Or, nous avons
démontré dans
le chapitre de Statistique lors de notre étude de l'intervalle de confiance
sur la variance avec moyenne empirique connue que: sont
des variables aléatoires normales (gaussiennes par hypothèse). Or, nous avons
démontré dans
le chapitre de Statistique lors de notre étude de l'intervalle de confiance
sur la variance avec moyenne empirique connue que:
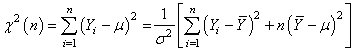 (136)
(136)
Donc:
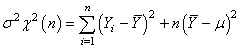 (137)
(137)
Donc:
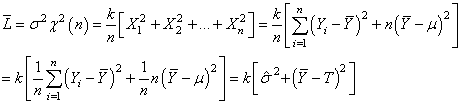 (138)
(138)
Cette dernière expression présente l'avantage de montrer très
clairement que pour minimiser la perte il faut agir sur la dispersion et l'ajustement
de la moyenne sur la valeur nominale.
Or nous avons démontré que (il est important dans les présents développements
que nous utilisions les notations qui distinguent les différents estimateurs!):
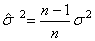 (139)
(139)
Donc:
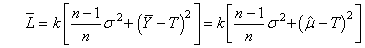 (140)
(140)
Et si n est grand nous avons alors pour un lot de produits:
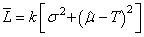 (141)
(141)
où le premier terme entre crochets représente donc l'écart-type
de Y autour
de sa propre moyenne et le deuxième terme la déviation de Y par
rapport à la cible T.
MAINTENANCE PRÉVENTIVE
L'évolution des techniques de production vers une plus grande robotisation
des systèmes techniques plus complexes a augmenté l'importance
de la fiabilité des machines de production. Aussi, un arrêt imprévu
coûte cher à une entreprise. De même, dans l'industrie aéronautique
et spatiale, les problèmes de fiabilité, de maintenabilité,
de disponibilité sont capitaux. La maintenance garantit le niveau de
fiabilité pour l'ensemble des composantes (mécaniques, électromécaniques
et informatiques).
L'existence d'un service de maintenance a pour raison le maintien des équipements
(systèmes) et aussi la diminution des pannes. En effet, ces dernières
coûtent cher, elles occasionnent :
- Des coûts d'intervention, de réparation
- Des coûts de non qualité du produit
- Des coûts indirects tels que des frais fixes, pertes de production,
la marge bénéficiaire perdu...
De ce fait, il faut tout mettre en oeuvre pour éviter la panne, agir
rapidement lorsqu'elle survient afin d'augmenter la disponibilité du
matériel. Pour ce faire, il faut modéliser la vie des équipements.
L'ensemble des méthodes et techniques relatives à ses problématiques
sont habituellement classifiées sous le nom de "Analyse
des Modes de Défaillance, des Effets et de leur Criticité" AMDEC.
Nous distinguons principalement deux classes de systèmes: les systèmes
non-réparables (satellites, bien de conommations à faibles coûts,
etc.) et les systèmes réparables (machines de production, moyens
de transports, etc.) où les approches théoriques sont différentes.
Pour la deuxième catégorie il est possible d'utiliser aussi les
chaînes de Markov, les réseaux de Petri ou la simulation par Monte-Carlo.
L'idée est dans les textes qui vont suivre de faire un petit point
sur ces méthodes, d'en rechercher l'efficacité et de permettre
au praticiens ingénieurs ou techniciens de mieux appréhender
ces problèmes. Une large place sera faite au modèle de Weibull
d'application importante dans le domaine.
ESTIMATEURS EMPIRIQUES
Dans le cadre de l'étude de fiabilité non accélérée
(le vieilissement accéléré est un sujet trop complexe
pour être abordé sur ce site), nous sommes amenés à définir
certaines variables dont voici la liste :
- sera
le nombre d'éléments bons à sera
le nombre d'éléments bons à  (instant
initial) (instant
initial)
-  le
nombre d'éléments bons à le
nombre d'éléments bons à 
-  le
nombre d'éléments défaillant entre le
nombre d'éléments défaillant entre  et et  noté aussi noté aussi 
-  l'intervalle
de temps observé égal à l'intervalle
de temps observé égal à  . .
Définitions:
D1. Nous définissons le "taux de défaillance
par tranche temporelle"  par
la relation : par
la relation :
 (142)
(142)
qui s''interprète donc comme étant le % d'éléments
défectueux par rapport au nombre d'éléments survivants
sur une tranche de temps donnée.
Cette dernière relation est aussi parfois appelée "hazard
ratio" (HR) ou
"survie relative".
D2. Nous définissons la "fonction de défaillance" par
la relation (densité de probabilité de défaillances à l'instant  )
: )
:
 (143)
(143)
en remarquant bien que le dénominateur n'est pas le même que
celui qui définit la taux de défaillance par tranche!
Cette fonction s'interprète donc comme étant le % d'éléments
défectueux dans la tranche de temps étudiée par rapport
au nombre total d'éléments initialement testés. Il s'agit
de l'indicateur qui intéresse le plus souvent l'ingénieur!
D3. Nous définissons naturellement la "fonction
de défaillance cumulée" par :
 (144)
(144)
que tend vers 1 lorsque le temps tend vers l'infini.
Cette fonction s'interprète donc comme étant le % d'éléments
défectueux cumulé par rapport au nombre total d'éléments
initialement testés.
D4. Nous définissons in extenso la "fonction
de fiabilité" par (il s'agit du deuxième terme de la
précèdente relation):
 (145)
(145)
Son nom provient par l'interpratition du rapport dans le cadre de la définition
de la fonction de défaillance cumulée.
Pour se rappeler des termes se souvenir que R provient de l'anglais "reliability" qui
signifie "fiabilité" alors que le F en anglais signifie "failure" qui
signifie en "panne".
Par suite nous avons aussi:
 (146)
(146)
Cette dernière relation servant au calcul des lois de fiabilité!
Puisque :
 et et  (147)
(147)
la fonction de défaillance peut être vue comme une probabilité ce
qui nous amène à définir naturellement son espérance
:
 (148)
(148)
Relation très utile dans la pratique qui donne en théorie le
pourcentage moyen d'éléments en panne à l'instant  . .
 Exemple: Exemple:
Nous avons relevé sur un lot de 37 moteurs d'un type donné les
défaillances suivantes répertoriées par tranches (données
par des clients ou mesuré en internes sur des bancs d'essais):
|
0 à
1'000 h.
|
1'000 à 2'000 h.
|
2'000 à
3'000 h.
|
3'000 à
4'000 h.
|
4'000 à
5'000 h.
|
5'000 à 6'000 h.
|
|
1 |
4 |
7 |
12 |
11 |
2 |
Tableau: 6
- Défaillances des moteurs par tranches d'effort
Il faut que nous estimions la valeur de la fonction de fiabilité  ,
la fonction de défaillance ,
la fonction de défaillance  et
la défaillance par tranche et
la défaillance par tranche  .
Les calculs sont élémentaires et nous obtenons le tableau suivant
: .
Les calculs sont élémentaires et nous obtenons le tableau suivant
:
|
Intervalle
d'observation |
Nombre de
défaillances dans l'intervalle |
Survivants |
Cumul des
défaillants |

|

|

|
|
0 |
- |
37 |
0 |
100% |
0 |
- |
0 à
1'000 h. |
1 |
36 |
1 |
97% |
2.7% |
27 |
1'000 à
2'000 h. |
4 |
32 |
5 |
86% |
10.8% |
111 |
2'000 à
3'000 h. |
7 |
25 |
12 |
67% |
18.9% |
218 |
| 3'000 à 4'000 h. |
12 |
13 |
24 |
35.1% |
32.4% |
480 |
| 4'000 à 5'000 h. |
11 |
2 |
35 |
5.4% |
5.4% |
846 |
5'000 à
6'000 h. |
2 |
0 |
37 |
0% |
- |
1 |
Tableau: 7
- Analyse des défaillances des moteurs par tranches d'effort
Nous voyons ci-dessus par exemple que le taux de défaillance n'est
pas constant bien évidemment!
Concernant les taux de défaillance, les ingénieurs reconnaissent souvent
trois tranches d'analyses suivant que certains objets étudiés soient jeunes,
en fonctionnement normal ou considérés en vieillissement.
On considère alors assez intuitivement (et parfois grossièrement) que le
taux de défaillance suit une courbe en baignoire comme représenté ci-dessous
(dans les tables techniques c'est souvent le taux de défaillance en fonctionnement
normal qui est donné):

(149)
alors que si vous observez le tableau précédent, le taux de
défaillance
ne suit pas du tout une courbe en baignoire (c'est donc un contre-exemple).
Les ingénieurs en fiabilité découpent souvent la baignoire en trois parties
visibles ci-dessus mais sous la dénomination technique suivante:
- D.F.R.: Decreasing Failure Rate (les composants jeune ayant des problèmes
de fabrication non identifiés lors de procédé sont éliminés
du lot ce qui a pour effet de diminuer le taux de défaillance). La loi
de Weibull est relativement bien adaptée pour modéliser cette phase.
- C.F.R.: Constant Failure Rate (les composants sont dans un état
stationnaire). La loi de Poisson est relativement bien adaptée pour
modéliser
les arrivées de pannes, et la loi exponentielle pour modéliser
le temps entre pannes successives..
- I.F.R.: Increasing Failure Rate (les composants sont en fin de vie et leur
taux de défaillance augmente). La loi de Weibulle est à nouveau relativement
bien adaptée pour modéliser cette phase.
Remarque: Contrairement
à ce que pas mal de théoriciens pensent..., les logiciels informatiques grand
public ont aussi leur taux de défaillance qui suit une courbe en baignoire. Effectivement,
au début il y a des bugs non détectés qui font que la défaillance va diminuer
au fur et à mesure de leur détection et leur correction. Ensuite,
à
cause
des mises-à-jour fréquentes de l'environnement qui ont tendance à rajouter
d'autres problèmes (service pack), le taux de défaillance se maintient à peu
près constant. Enfin, avec le temps, l'évolution des
technologies
environnantes (framwork) rendent l'applicatif obsolète et des fonctions ne
répondent ou n'agissent plus correctement ce qui fait à nouveau augmenter le
taux de défaillance.
Vis-à-vis de l'efficacité de la rénovation, indiquons qu'elles peuvent (en
simplifiant) très fréquemment se ranger en trois catégories:
1. As good as new: C'est de la maintenance préventive dans le sens que nous
changeons une pièce lorsque sa durée de vie l'amène à une taux de défaillance
que nous considérons comme trop élevé et dont la rupture non anticipée coûtera
plus cher que sa non-anticipation.
2. As bad as old: C'est de la maintenance déficiente dans le sens que nous
changeons une pièce que lorsqu'elle est arrivée à rupture ce qui engendre majoritairement
des coûts d'arrêts plus élevés que la maintenance préventive qui consiste elle à anticiper
au plus juste la casse.
3. Restauration partielle: C'est de la maintenance préventive minimale dans
les sens que nous réparons la pièce défaillante plutôt que de la remplacer
par une nouvelle. A nouveau le problème du coût doit être calculé en faisant
un audit des besoins et des délais de l'entreprise.
Revenons en à d'autres définitions au passage à la limite
du continu.
Nous savons donc que le "taux de défaillance instantané" aura
pour unité l'inverse du temps tel que 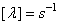 .
Ce taux est dans le cadre de notre étude pas nécessairement constant dans le
temps nous l'avons constaté! .
Ce taux est dans le cadre de notre étude pas nécessairement constant dans le
temps nous l'avons constaté!
Soit R(t) le pourcentage cumulé d'objets analysés
toujours en état de bon fonctionnement d'un échantillon testé au temps t.
Le nombre d'objets tombant en panne durant le temps infinitésimal dt est
donc égal à :
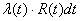 (150)
(150)
ce qui correspond donc à la diminution du stock initial en bon fonctionnement
au temps t.
Nous pouvons alors écrire la relation:
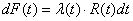 (151)
(151)
soit :
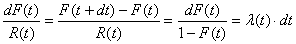 (152)
(152)
Définition: La "probabilité conditionnelle
de défaillance" (rien à voir avec les probabilités
conditionnelles cependant....) entre t et t + dt est
définie par:
 (153)
(153)
où F(t) et R(t) sont respectivement
la fonction cumulée de défaillance (probabilité cumulée
de tomber en panne au temps t) et la fonction fiabilité appelée également "fonction
de survie". R(t) valant 1 au temps 0 et... 0
après
un temps infini comme nous l'avons déjà vu avant!
Dès lors,  peut
s'interpréter comme la défaillance instantanée! En analyse
de survie, le facteur de dt est nommé aussi parfois "fonction
de risque". peut
s'interpréter comme la défaillance instantanée! En analyse
de survie, le facteur de dt est nommé aussi parfois "fonction
de risque".
Remarque: Par
la même démarche intelectuelle, plutôt que de définir
une fonction de défaillance F(t) et de survie R(t)
avec sa fonction de risque, nous pouvons définir une fonction de réparibilité avec
sa fonction de M(t) qui serait alors une "fonction
de maintenabilité".
Si nous intégrons (attention u représente maintenant
le temps!) :
 (154)
(154)
Comme  nous
avons : nous
avons :
 (155)
(155)
d'où :
 (156)
(156)
Par ailleurs, puisque nous avons vu que  ,
nous avons alors la "fonction de densité/répartition
de défaillance instantanée": ,
nous avons alors la "fonction de densité/répartition
de défaillance instantanée":
 (157)
(157)
Nous pouvons obtenir cette relation et interprétation sous une autre
manière:
 (158)
(158)
où nous retrouvons donc F(t) la fonction de probabilité cumulée
de défaillance. Evidemment pour déterminer la loi f(t),
nous utilisons les outils statistiques d'ajustements habituels (cf.
chapitre de Statistiques).
Nous avons alors la relation très importante (voir la plus importante!) dans
la pratique que relie la loi de densité de la loi de fiabilité:
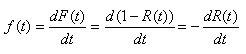 (159)
(159)
Nous avons ci-dessus les trois expressions les plus générales liant les lois
de fiabilité et le taux instantané de défaillance.
Puisque f(t) est la fonction de densité de défaillance
au temps t, nous pouvons introduire la "moyenne
du temps de bon fonctionnement" (M.T.B.F. qui provient de l'anglais:
Mean Time Between Failures) qui n'est que l'espérance mathématique
de la défaillance
dans le cas où le temps de réparation ou de changement est considéré comme
négligeable:
 (160)
(160)
Ainsi, si la répartition des pannes est équiprobable (fonction
de densité uniforme), ce qui est plutôt rare, la moitié des équipement
seront hors service à M.T.B.F.
Remarque: En
observant 100'000 disques durs, des ingénieurs de Google
auraient observé en moyenne 8% de pertes par an! Donc un taux de perte
plus élevé qu'avec
le M.T.B.F. annoncé des fabricants qui serait d'environ 300'000 heures!
Le taux de perte est plus élevé les
3 premières années! Mais peut être que les disques qui
survivent vivent plus longtemps!
Si le temps de réparation ou de changement est pas négligeable,
il faut remplacer la M.T.B.F. par la MUT (voir plus bas la signification
des ces abréviations) car ces deux-ci sont alors considérées
comme égales.
Nous
avons aussi en utilisant l'intégration par parties et la relation précédente:

Donc une autre manière de l'exprimer:
 (161)
(161)
Nous avons donc la relation:
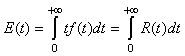 (162)
(162)
d'où le fait que certains calculent une approximation de la MTBF
en faisant une simple moyenne arithmétique des temps entre panne d'un
système réparable!
Par ailleurs, il faut savoir que certains y incluent le temps de réparation
et d'autres pas... (car le premier cas est assez difficile à obtenir).
Au fait, mathématiquement le M.T.B.F. calculé ne devrait pas
comprendre pas le temps de réparation!
Nous avons alors en approximation pour un composant réparable qui est vendu
à des consommateurs:
(163)
soit de manière abrégée sous la forme:
(164)
Il est nécessaire avant d'aller plus loin de donner quelques indications
sur les termes employés, en particulier pour les M.T.B.F. (Mean
Time Between Failures), M.U.T. (Mean Up Time), M.T.T.R. (Mean Time To
Repair), M.D.T. (Mean
Down Time).
Pour les matériels réparables,
nous avons le chronogramme type ci-dessous où le lecteur remarquera
qu'il est équivalent de définir le M.T.B.F. comme étant
le temps entre la fin de deux pannes soit entre le début de deux
pannes (et en interne d'une entreprise on y inclut le
temps de réparation, dans le cas contraire d'un produit vendu
on inclut pas le temps de réparation):
(165)
et pour les matériels non réparables avec le M.T.T.F. (Mean Time To Failure):
(166)
Pour ceux faisant de la maintenant préventive, nous
ajoutons également la M.T.B.R. (Mean Time Between Removal) ou M.T.B.M.
(Mean Time Beetween Maintenance) qui idéalement pour une machine complexe
doit être
le plus grand possible si elle est de bonne qualité.
Remarques:
R1. En ce tout début de 21ème
siècle les pays
devraient en toute rigueur légiférer
pour obliger tous les industriels à communiquer la M.T.T.F. et M.T.B.F.
de leurs produits afin que le consommateur puisse mieux faire son choix à l'achat
et comparer les valeurs par rapport à la garantie fournie! Malheureusement
ce n'est pas le cas et cela permettrait de mettre en évidence une
mauvaise tradition actuelle dans l'industrie des produits grand public qui
est de fabriquer
des composants
dont
la durée
de vie tourne autour des 200'000 heures afin d'assurer aux industriels
un renouvellement de leur
marché.
R2. L'expression anglaise Mean Time Between Failures est parfois
traduite à tort en français par "Moyenne des Temps de
Bon Fonctionnement ". Mais le temps moyen entre deux défaillances
intègre dans son calcul les temps de réparation et de maintenance,
alors que la moyenne des temps de bon fonctionnement ne les intègre
pas!
R3. Pour un composant non réparable certains constructeurs
communiquent la M.T.B.F. quand même... qui est en toute rigueur alors égale à la
M.T.T.F. Mais sinon dans un cas général, la M.T.T.F est bien
plus longue que la M.T.B.F..
Certains industriels mettent alors dans la datasheet de leurs
produits le "taux de disponibilité" défini par:
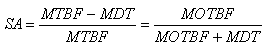 (167)
(167)
et dont le but est qu'il soit le plus proche possible de 1
(c'est-à-dire de faire tendre vers zéro le MTTR).
La classification des systèmes en termes de disponibilité conduit
communément à 7 classes de non prise en compte (système
disponible 90% du temps, et donc indisponible plus d'un mois par an) à ultra
disponible (disponible 99.99999% du temps et donc indisponible seulement 3
secondes par an): ces différentes classes correspondent au nombre de
9 dans le pourcentage de temps durant lequel les systèmes de la classe
sont disponibles (une année comporte 525'600 minutes):.
Type |
Indisponibilité
(minutes par an) |
Pourcentage disponibilité |
Classe |
non géré |
50'000
(~35 jours) |
90% |
1 |
géré |
5'000
(~3.5 jours) |
99% |
2 |
bien géré |
|
99.9% |
3 |
tolérence fautive |
50 |
99.99% |
4 |
haute disponibilité |
5 |
99.999% |
5 |
très haute disponibilité |
0.5 |
99.9999% |
6 |
très grande haute disponibilité |
0.05 |
99.99999% |
7 |
Tableau: 8
- Classes de défaillances AMDEC
L'usage de ces paramètres dans le cadre de fiabilité font
dire que nous avons une "approche en valeurs moyennes".
Signalons enfin un cas simple: Certains composants (électroniques typiquement)
ont dans leur période de maturité un taux de défaillance constant. La loi de
probabilité cumulée de la défaillance qui en découle s'en
déduit alors immédiatement puisque  : :
 (168)
(168)
La fonction de densité des éléments défaillants
au temps t est alors:
 (169)
(169)
Elle suit donc une loi exponentielle! Cette loi et ses moments nous sont
connus (cf. chapitre de Statistiques). Il devient
alors facile déterminer le MTTF (dans un cas non réparable, sinon nous
parlerons de la MTBF) et son écart-type
(inverse du taux de défaillance) ainsi qu'un intervalle de confiance.
Par ailleurs, si nous calculons la fiabilité R(t)
au temps correspondant à la MTTF pour un matériel non réparable
ou MTBF pour un matériel réparable (inverse du taux de défaillance
dans le cas de la loi exponentielle) nous obtiendrons toujours une probabilité cumulée
de 36.8% (donc en gros une chance sur trois de fonctionner à ce moment
là et 2 chances sur 3 de tomber en panne) et non de 50% comme on peut
le penser intuitivement (ce qui est le cas seulement si la loi de probabilité est
symétrique).
Etant donné que les tables techniques de fiabilité dans l'industrie
supposent presque toujours le taux de fiabilité constant alors nous
comprenons mieux l'importance de celle-ci (nous en auronts un exemple lors
de notre présentation des topologies de systèmes).
Rappellons aussi que nous avons vu dans le chapitre de Probabilités
que si nous avons un ensemble d'événements indépendants
(mécanismes indépendants) avec une probabilité donnée,
alors les probabilités calculées sur l'ensemble dans sa totalité implique
la multiplication des probabilités.
Donc dans un mécanisme ayant des pièces indépendantes
mais essentielles (système dit en "série") la fonction
de densité de fiabilité globale sera égale à la
multiplication des lois de probabilités cumulées R(t)
et ce qui équivaut donc dans le cas d'une loi exponentielle d'avoir
une seule loi exponentielle dont le taux de défaillance global est égal à la
somme des taux de défaillances des différentes pièces.
Un autre exemple: En mécanique, où le phénomène d'usure est à l'origine de
la défaillance, le taux de défaillance est souvent du type linéaire (il augement
donc de manière constant avec le temps et est non nul lors du premier
allumage de l'appareil):
 (170)
(170)
Alors:
 (171)
(171)
Soit:
 (172)
(172)
Comme:
 (173)
(173)
cette intégrale ne peut se calculer ques par une méthode numérique. Dès
lors on préfère prendre des lois rapprochées à l'aide
d'ajustement du Khi-Deux comme par exemple la loi de Weibull qui est un peu
la poubelle à tout mettre dans le domaine..
Il faus savoir que dans les banques de données de fiabilité communes
et gratuitement disponibles sur le marché sont normalement donnés:
la dénomination du matériel ou du composant, la MTBF, la taux
de défaillance moyen, le patrimoine statistique, un coefficient multiplicatif
du taux de défaillances dépendant de l'environnement ou des contraintes
d'utilisation.
MODÈLE DE WEIBULL
Encore une fois, les techniques de maintenances utilisent les probabilités
et statistiques donc nous renvoyons le lecteur au chapitre du même nom.
Cependant, il existe dans le domaine de la maintenance (et pas seulement) une
fonction de densité de probabilité très utilisée
appelée "loi de Weibull".
Elle est complètement empirique et est définie par :
 (174)
(174)
où  avec avec  qui
sont respectivement appelés "paramètre
d'échelle" qui
sont respectivement appelés "paramètre
d'échelle"  , "paramètre
de forme" , "paramètre
de forme"  et "paramètre
d'emplacement" et "paramètre
d'emplacement"  . .
La loi de Weibull est aussi souvent notée sous la forme suivante en posant  , ,  , ,  : :
 (175)
(175)
Elle peut être calculée dans MS Excel. sous cette
dernière forme en utilisant la fonction LOI.WEIBULL( ).
Remarque: Elle
peut être vue comme une généralisation de la fonction de
distribution exponentielle avec l'avantage qu'il est possible de jouer avec
les trois paramètres de manière à obtenir presque n'importe
quoi.
(176)
En annulant  ,
nous obtenons la "distribution de Weibull à deux
paramètres" : ,
nous obtenons la "distribution de Weibull à deux
paramètres" :
 (177)
(177)
qui a une application pratique importante et dont nous avons calculé les estimateurs
des paramètres dans le chapitre de Statistiques.
 Exemple: Exemple:
Dans le diagramme ci-dessous, nous avons pour  étant
égal à zéro: en
rouge, en
vert, en
noir, en bleu , en
magenta : étant
égal à zéro: en
rouge, en
vert, en
noir, en bleu , en
magenta :
(178)
et le tracé de la fonction de distribution et respectivement de répartition
de la loi de Weibull de paramètre avec  nul: nul:
(179)
En posant encore une fois  et
en assumant que et
en assumant que  nous
avons la "distribution de Weibull à un paramètre" : nous
avons la "distribution de Weibull à un paramètre" :
 (180)
(180)
où le seul paramètre inconnu est le paramètre d'échelle  .
Nous assumons que le paramètre .
Nous assumons que le paramètre  est
connu à priori de expériences passées sur des échantillons
identiques. est
connu à priori de expériences passées sur des échantillons
identiques.
Nous retrouvons également parfois cette relation dans la littérature sous
la forme:
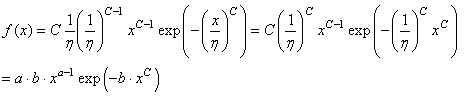 (181)
(181)
Le MTBF est alors donnée par l'espérance de la loi de Weibull
avec  non
nul: non
nul:
 (182)
(182)
Posons :
 (183)
(183)
avec :
 (184)
(184)
Ce qui donne :
 (185)
(185)
La première intégrale nous est déjà connue, nous
l'avons déjà vue dans le chapitre de Calcul Différentiel.
Il s'agit simplement de la fonction gamma d'Euler :
 (186)
(186)
Nous avons finalement :
 (187)
(187)
En annulant  il
vient le cas courant en fiabilité: il
vient le cas courant en fiabilité:
 (188)
(188)
Remarque: Si
par le plus grand des hasards  ,
alors comme nous l'avons démontré lors de notre étude
de la fonction Gamma d'Euler :
 (189)
(189)
Dans le cas où  il
faut faire appel aux tables numériques obtenues par les algorithmes
vus dans le chapitre de Méthodes Numériques. il
faut faire appel aux tables numériques obtenues par les algorithmes
vus dans le chapitre de Méthodes Numériques.
De même :
 (190)
(190)
Finalement :
 (191)
(191)
Remarque: Certains
spécialistes, lorsqu'il est fait usage des deux moments d'ordre deux dans
l'analyse probabiliste de la défaillance, parlent parfois "d'approche
en moyenne quadratique"...
TOPOLOGIE DES SYSTÈMES
Lorsque nous travaillons avec des systèmes réels non réparables
(mécaniques, électroniques
ou autres), nous sommes confrontés à des contraintes différentes
suivant le type de montage que nous avons. L'étude de ce type de systèmes
est aussi appelé "Reliability Block Diagramm".
Les deux hypothèses principales de l'étude de ces systèmes sont:
H1. La panne d'un composant est indépendante des autres
H2. Pas de pannes arrivant conjointement
Nous reconnaissons 5 topologies principales dont chaque composant est représenté
par un bloc:
T1. Topologie série:
Si un seul composant est défectueux le système ne fonctionne plus (les exemples
sont tellement nombreux et simples à trouver que nous n'en citerons pas).
Alors dans l'hypothèse où la panne d'un composant est indépendante des autres,
la probabilité cumulée de défaillance est égale au produit des probabilités
cumulées (cf. chapitre de Probabilités).

(192)
Comme souvent il est fait usage de la loi exponentielle, la multiplication
de plusieurs termes de probabilités cumulées étant relativement longue à écrire,
nous lui préférons l'utilisation de la probabilité de fiabilité cumulée R.
Ainsi, la fiabilité (probabilité de fonctionnement) d'un système
série
est donnée
par:
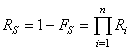 (193)
(193)
Ce qui nous amène bien à une valeur nulle pour la fiabilité si
au minimum un bloc a une fiabilité nulle.
Ce qui se note traditionnellement dans le domaine:
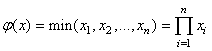 (194)
(194)
Remarque: Le lecteur attentif aura remarque que
le système série est toujours moins fiable que sa composant la
moins fiable! Attention!! Dans le cas des composantes électroniques, le taux de défaillance
est souvent considéré comme constant par souci de simplification et la fonction
de densité est alors celui de la loi exponentielle:
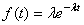 (195)
(195)
Or, nous avons démontré que dans le cas d'un système non réparable:
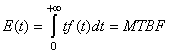 (196)
(196)
Et comme nous avons démontré dans le chapitre de Statistique que l'espérance
de la loi exponentielle est:
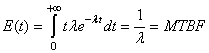 (197)
(197)
Nous avons aussi démontré plus haut que:
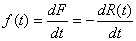 (198)
(198)
Donc:
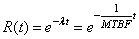 (199)
(199)
Alors pour un système série à taux de défaillance constant:
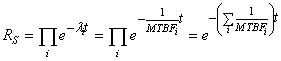 (200)
(200)
Ainsi, dans ce cas particulier:
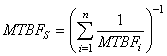 (201)
(201)
et... le problème sur Internet c'est que les pages web qui parlent de système à topologie
série (ou parallèle) font implicitement usage d'une loi exponentielle d'où parfois
de grosse erreurs de la part des praticiens qui utilisent cette dernière relation
sans avoir étudié les détails mathématiques sous-jacents.
T2. Topologie parallèle:
Contrairement au système précédent, le système continue à fonctionner
si au moins un composant fonctionne (typiquement les systèmes de redondance
dans les avions, les fusées ou les centrales nucléaires).

(202)
En d'autres termes, il s'arrête de fonctionner si et seulement si:
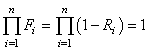 (203)
(203)
Donc il vient immédiatement que:
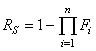 (204)
(204)
Nous avons donc pour le système parallèle dont les composantes sont à taux
de défaillance constant et tous identiques (pour simplifier l'étude):
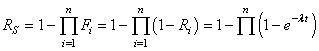 (205)
(205)
Nous avons alors:
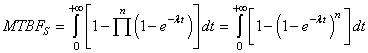 (206)
(206)
En posant:
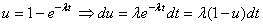 (207)
(207)
et en remplaçant dans l'expression antéprécédente nous avons:
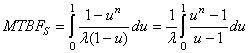 (208)
(208)
Il n'est pas possible d'intégrer cette dernière relation de manière formelle
mais si on compare pour différentes valeurs de n fixées alors nous voyons
très vite que:
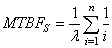 (209)
(209)
T3. Topologie k/n:
Ce système fonctionne si k parmi n composants de même loi de
fiabilité R fonctionnent. C'est typiquement le cas des disques RAID
en informatique pour lesquels il en faut plus d'un qui fonctionne toujours à la
fin et ce nombre est déterminé par le volume de données.
Nous avons alors la représentation schématique suivante:

(210)
Donc chercher la loi de probabilité cumulée de fiabilité revient à se
poser la question de la probabilité cumulée d'avoir k éléments
qui fonctionnent parmi n qui sont non distinguables.
Cela revient donc à utiliser la loi binomiale (cf.
chapitre de Statistiques) pour laquelle nous avons démontré que la
probabilité cumulée était donnée alors par:
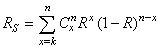 (211)
(211)
T4. Topologie série/parallèle et parallèle/série à configuration symétrique:
Ce sont simplement des compositions simples de des deux premiers systèmes étudiées
précédemment.
Nous avons d'abord le système série/parallèle:

Or, comme les systèmes séries sont donnés par:
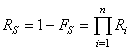 (212)
(212)
et les parallèles par:
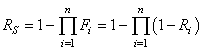 (213)
(213)
la composition des deux donne trivialement dans notre cas ci-dessus:
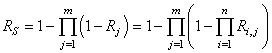 (214)
(214)
Et nous avons dans la famille aussi le système parallèle/série:

(215)
où en utilisant exactement la même démarche que précédemment nous avons:
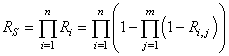 (216)
(216)
T5. Topologie complexe:
Au fait, il ne s'agit pas vraiment de systèmes complexes mais ils nécessitent
simplement une petite maîtrise des axiomes de probabilités. L'exemple particulier
qui va nous intéresser est le suivant (typiquement filtre RLC en cascade):

(217)
dénommé "réseau avec bridge".
Et nous devinons que ce qui rend le système complexe est le composant 5.
Nous pouvons alors considérer une première approche qui est de décomposer le
problème.
Le système par rapport au composant 5 sera soit dans l'état:

(218)
s'il est défectueux avec une loi de densité probabilité:
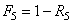 (219)
(219)
et ayant lui-même une fiabilité de:
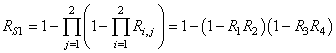 (220)
(220)
selon nos résultats précédents du système complexe série/parallèle.
Soit dans l'état suivant s'il est fonctionnel avec une loi de densité probabilité 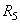 : :
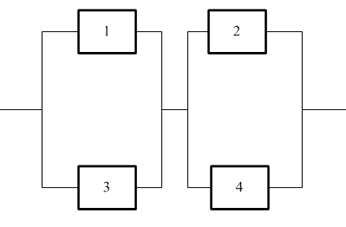
(221)
et ayant lui-même une fiabilité de:
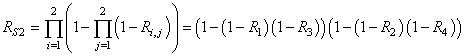 (222)
(222)
selon nos résultats précédents du système complexe parallèle/série.
Comme le système ne peut pas être dans les deux états en même temps, nous
avons affaire à une probabilité disjointe (cf. chapitre
de Probabilités) soit la somme des densités auxquelles nous devons associer
les autres composants. Dès lors nous avons:
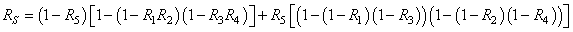 (223)
(223)
Nous pouvons alors à l'aide de l'ensemble des 5 topologies précédentes faire
une évaluation de la fiabilité d'un système quelconque!
Une autre stratégie pour les systèmes complexes consiste
de les décomposer en système séries
ou parallèles simples. Si cela n'est pas possible, nous pouvons calculer
la fiabilité de chaque configuration du système qui est considérée
comme fonctionnant et faire ensuite la somme des probabilités de fonctionnement
de chaque configuration.
Faisons un exemple en considérant le cas particulier suivant:

(224)
Et considérons la table de vérité suivante avec les 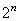 configurations
possibles: configurations
possibles:
Etat n° |
Bloc 1 |
Bloc 2 |
Bloc 3 |
Sortie |
1 |
0 |
0 |
0 |
0 |
2 |
1 |
0 |
0 |
0 |
3 |
0 |
1 |
0 |
0 |
4 |
1 |
0 |
1 |
1 |
5 |
0 |
1 |
1 |
1 |
6 |
1 |
1 |
1 |
1 |
7 |
1 |
1 |
0 |
0 |
8 |
0 |
0 |
1 |
0 |
Tableau: 9 - Table de vérité d'un système de maintenance préventive
Le principe (il faut le savoir...) consiste à dire qu'un état UP (valant
donc: 1) est affecté à la valeur 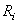 du
bloc i concerné et que l'état DOWN (valant donc: 0) est affecté à la
valeur du
bloc i concerné et que l'état DOWN (valant donc: 0) est affecté à la
valeur 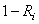 du
bloc i. Chaque valeur sera multipliée avec les autres pour obtenir la
fiabilité totale du système à un état donné. du
bloc i. Chaque valeur sera multipliée avec les autres pour obtenir la
fiabilité totale du système à un état donné.
Ainsi, dans l'exemple précédent, nous avons donc que 3 états qui permettent
au système de fonctionner. Calculons leur fiabilité respective. Les états n°4
et n°5 donnent donc par définition:
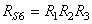 (225)
(225)
L'état n°6 donne lui par définition:
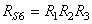 (226)
(226)
et nous sommons le tout comme indiqué ultérieurement:
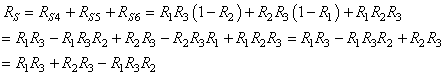 (227)
(227)
Et nous pouvons vérifier que cette approche est effectivement correcte en
prenant la relation générale d'un tel système démontrée plus haut:
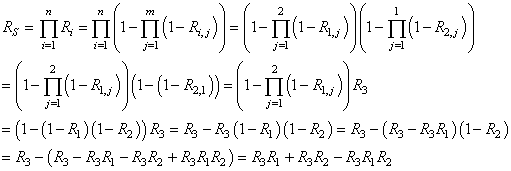 (228)
(228)
ce qui montre que nous avons bien le même résultat et que l'approche par
décomposition fonctionne aussi.
Enfin, signalons pour terminer que lorsque nous incluons dans les systèmes
des éléments qui permettent de tolérer ou d'accepter certaines erreurs nous
parlons alors de "tolérance aux fautes" et
nous en distinguons principalement de trois types:
- Redondance active: Dans ce cas tous les composants redondants fonctionnent
en même temps.
- Redondance passive: Un seul élément redondant fonctionne, les autres sont
en attente, ce qui a pour avantage de diminuer ou de supprimer le vieillissement
des éléments redondants mais en contrepartie nécessite l'insertion d'un composant
de détection de panne et de commutation.
- Redondance majoritaire: Cette redondance concerne surtout des signaux.
Le signal de sorite sera celui de la majorité des composants redondants.
MÉTHODE ABC
Dans une entreprise, les tâches sont nombreuses et les équipes d'entretien
et de maintenant sont systématiquement réduites à leur minimum dans les temps
qui courent.
De plus, les technologies les plus évoluées en matière de maintenance coûtent
cher ou peuvent coûter très cher, et ne doivent pas être appliquées sans discernement.
Il convient par conséquent de s'organiser de façon efficace et rationnelle.
L'analyse ABC, utilisant implicitement la loi de probabilité cumulée
de Pareto (cf. chapitre de Statistiques), permet
d'y remédier
relativement bien. Ainsi, un classement des coûts par rapport aux types de
panne donne des priorités sur les interventions à mener (cette méthode
empirique est aussi utilisée dans de nombreux autres domaines dont un qui est
très connu: la gestion de stocks).
L'idée consiste dans un premier temps comme pour l'analyse de Pareto (cf.
chapitre de Techniques de Gestion) de classer les pannes par ordre
croissant de coût de maintenance (ou de coût d'impact en cas de panne) chaque
panne se rapportant un système simple ou complexe et à établir un graphique
faisant correspondre les pourcentages de coûts cumulées aux pourcentages
de type de panne cumulés.
Ensuite, nous distinguons par tradition trois zones:
- Zone A: Dans la majorité des cas, environ 20% des pannes représentent 80%
des coûts et il s'agit donc de la zone prioritaire.
- Zone B: Dans cette tranche, les 30% de pannes suivantes coûtent 15% supplémentaires.
- Zone C: 50% des pannes restante ne revient qu'à 5% des coûts.
Voyons un exemple en considérant que les données suivantes ont été recueillies
et que nous aimerions faire une analyse du % de machines sur lesquelles il
faudrait que nous nous concentrions pour diminuer le coût d'heures de pannes
d'environ 80% (dans la réalité on s'intéressera plus au % du coût financier!).
N° de Machine |
Heures d'arrêt |
Nb. de pannes |
Machine n°1 |
100 |
4 |
Machine n°2 |
32 |
15 |
Machine n°3 |
50 |
4 |
Machine n°4 |
19 |
14 |
Machine n°5 |
4 |
3 |
Machine n°6 |
30 |
8 |
Machine n°7 |
40 |
12 |
Machine n°8 |
80 |
2 |
Machine n°9 |
55 |
3 |
Machine n°10 |
150 |
5 |
Machine n°11 |
160 |
4 |
Machine n°12 |
5 |
3 |
Machine n°13 |
10 |
8 |
Machine n°14 |
20 |
8 |
Tableau: 10
- Analyse ABC sur pannes machines
Ensuite, dans MS Excel ou ailleurs nous pouvons aisément établir le tableau
suivant:
Machine |
Arrêt [h.] |
Cumul [h.] |
%Cumulé |
Pannes |
Cumul pannes |
%Cumulé |
11 |
160 |
160 |
21.19% |
4 |
4 |
4.30% |
10 |
150 |
310 |
41.06% |
5 |
9 |
9.68% |
1 |
100 |
410 |
54.30% |
4 |
13 |
13.98% |
8 |
80 |
490 |
64.90% |
2 |
15 |
16.13% |
9 |
55 |
545 |
72.19% |
3 |
18 |
19.35% |
3 |
50 |
595 |
78.81% |
4 |
22 |
23.66% |
7 |
40 |
635 |
84.11% |
12 |
34 |
36.56% |
2 |
32 |
667 |
88.34% |
15 |
49 |
52.69% |
6 |
30 |
697 |
92.32% |
8 |
57 |
61.29% |
14 |
20 |
717 |
94.97% |
8 |
65 |
69.89% |
4 |
19 |
736 |
97.48% |
14 |
79 |
84.95% |
13 |
10 |
746 |
98.81% |
8 |
87 |
93.55% |
12 |
5 |
751 |
99.47% |
3 |
90 |
96.77% |
5 |
4 |
755 |
100.00% |
3 |
93 |
100.00% |
Tableau: 11
- Normalisation des données pour analyse ABC
Nous avons alors graphiquement:

(229)
où les zones A, B et C sont arrondis à des points existants.
Ainsi, la zone critique A compte les machines 11, 10, 1, 8, 9 et 3.
Une amélioration de la fiabilité de ces machines peut donc procurer jusqu'à 78.8%
de gain de temps sur les pannes.
Maintenant déterminons les paramètres de la loi de répartition de Pareto:
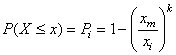 (230) (230)
Nous devons déterminer 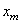 et k les
autres paramètres nous sont donnés par nos mesures (le tableau). et k les
autres paramètres nous sont donnés par nos mesures (le tableau).
Nous pouvons jouer de la manière suivante:
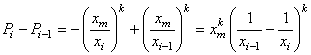 (231) (231)
d'où:
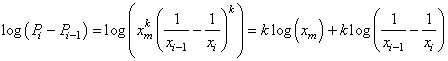 (232) (232)
Donc à l'aide de:
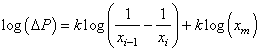 (233)
(233)
on doit pouvoir déterminer les deux paramètres recherchés en considérant
l'expression comme l'équation d'une droite dont k est la pente et 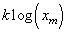 l'ordonnée à l'origine: l'ordonnée à l'origine:
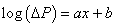 (234) (234)
Une régression linéaire simple (cf. chapitre de Méthodes
Numériques) nous donne:
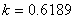 et et 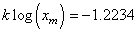 (235)
(235)
donc:
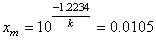 (236) (236)
Nous avons donc au final:
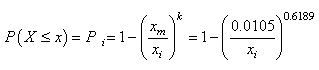 (237)
(237)
Ce qui donne alors le tableau suivant (les xi de la loi de Pareto sont les
%Cumulé de panne):
Machine |
%Cumulé coûts [h.] |
%Cumulé panne |
%Cumulé loi Pareto |
11 |
21.19% |
4.30% |
61.76% |
10 |
41.06% |
9.68% |
78.01% |
1 |
54.30% |
13.98% |
82.89% |
8 |
64.90% |
16.13% |
84.48% |
9 |
72.19% |
19.35% |
86.29% |
3 |
78.81% |
23.66% |
88.05% |
7 |
84.11% |
36.56% |
91.12% |
2 |
88.34% |
52.69% |
93.08% |
6 |
92.32% |
61.29% |
93.75% |
14 |
94.97% |
69.89% |
94.29% |
4 |
97.48% |
84.95% |
95% |
13 |
98.81% |
93.55% |
95.32% |
12 |
99.47% |
96.77% |
95.43% |
5 |
100.00% |
100.00% |
95.53% |
Tableau: 12
- Comparaisons données expérimentales/théoriques
Nous pouvons alors obtenir la vraie courbe de Pareto correspondante facilement
dans MS Excel:

(238)
La différence entre l'expérimentale est la théorique est non
négligeable... Comme k est inférieur à 1, alors comme nous l'avons vu
démontré dans le chapitre de Statistiques, la loi de Pareto n'a ni espérance,
ni variance.
Il faut faire attention au fait que dans le domaine de la gestion la loi
de Pareto est utilisée un peut à torts et à travers alors que une autre loi
de probabilité pourrait être beaucoup plus adaptée.
Par ailleurs, un simple test d'ajustement du Khi-Deux (cf.
chapitre de Statistiques) nous montre qu'il faut rejeter l'approximation
par une loi de Pareto. Par ailleurs des logiciels spécialisés comme @Risk
rejettent l'approximation par Pareto au-delà des 20 meilleurs ajustements,
le meilleur ajustement étant selon ce même logiciel une loi log-normale.
PLANS D'EXPÉRIENCE
Le comportement des produits industriels est généralement fonction
de nombreux phénomènes, souvent dépendants les uns des
autres. Pour prévoir ce comportement, le produit et les phénomènes
sont modélisés, et des simulations sont effectuées. La
pertinence des résultats des simulations dépend évidemment de
la qualité des
modèles.
En particulier, dans le cadre de la conception ou reconception d'un produit,
les modèles font généralement intervenir un certain nombre
de grandeurs physiques (paramètres) que l'on s'autorise à modifier.
Le comportement des produits industriels est généralement
fonction de nombreux phénomènes, souvent dépendants les
uns des autres. Pour prévoir ce comportement, le produit et les phénomènes
sont modélisés, et des simulations sont effectuées.
Or, ces essais sont coûteux, et ce d'autant plus que le nombre de paramètres à faire
varier est important. En effet, la modification d'un paramètre peut
par exemple exiger un démontage et un remontage du produit, ou bien
la fabrication de plusieurs prototypes différents (cas d'une pièce
produite en série), ou encore l'interruption de la production pour changer
d'outil (cas d'un process de fabrication)... Le coût d'une étude
expérimentale dépend donc du nombre et de l'ordre des essais
effectués.
L'idée consiste alors à sélectionner et
ordonner les essais afin d'identifier, à moindres coûts, les effets
des paramètres sur la réponse du produit. Il s'agit de méthodes
statistiques faisant appel à des notions mathématiques simples
le plus souvent. La mise en oeuvre de ces méthodes comporte trois étapes
:
1. Postuler un modèle de comportement du système (avec des
coefficients pouvant être inconnus)
2. Définir un protocole d'expérience,
c'est-à-dire une série
d'essais permettant d'identifier les coefficients du modèle
3. Faire
les essais, identifier les coefficients et conclure.
Les plans d'expériences ("Design of Experiment" (D.O.E.)
en anglais abrégés PEX en français) permettent d'organiser au mieux les essais
qui accompagnent une recherche
scientifique ou des études industrielles. Ils sont applicables à de
nombreuses disciplines et à toutes les industries à partir du moment où l'on
recherche le lien qui existe entre une grandeur d'intérêt, y (quantité de
rebus, défauts, détections, amplitude, etc.), et des variables 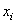 dans
un but d'optimisation. Raison pour laquelle il existe des logiciels
pour les traiter comme MiniTab ou principalement JMP pour ne citer que les
plus connus. dans
un but d'optimisation. Raison pour laquelle il existe des logiciels
pour les traiter comme MiniTab ou principalement JMP pour ne citer que les
plus connus.
Indiquons également que les plans d'expérience sont un des
pilier de la chimiométrie
(outils mathématiques, en particulier statistiques, pour obtenir
le maximum d'informations à partir des données chimiques).
Il existe trois grandes familles de plans d'expériences:
1. Les "plans de criblages": dont l'objectif est de découvrir
les facteurs les plus influents sur une réponse donnée en un
minimum d'expériences. C'est la plus simples des familles car proche
de l'intuition expérimentale (elle est parfois considérée
comme une sous-famille de la deuxième famille).
2. Les "plans de modélisation": dont l'objectif est de trouver
la relation mathématique qui lie les réponses mesurées
aux variables associés aux facteurs soit via une démarche mathématique
analytique ou purement matricielle. Les plans factoriels complets et fractionnaires
(2 niveaux par facteurs avec modèles linéaires) ainsi que les
plans pour surfaces de réponse (au moins 3 niveaux par facteurs avec
modèles du second degré) font partie de cette famille.
3. Les "plans de mélange": dont l'objectif est le même
que la deuxième famille mais où les facteurs ne sont pas indépendants
et sont contraints (par exemple leur somme/ ou leur rapport doit être égale à une
certaine constante).
Le principe global se base sur le fait que l'étude d'un phénomène
peut, le plus souvent, être schématisé de la manière suivante
: nous nous intéressons à une
grandeur, y qui dépend d'un grand nombre de variables, 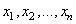 (et
leur ordre n'a pas d'influence... ce qui est par contre problématique
en chimie...). (et
leur ordre n'a pas d'influence... ce qui est par contre problématique
en chimie...).
La modélisation mathématique consiste à trouver une fonction f telle
que:
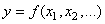 (239)
(239)
qui prenne en compte l'influence de chaque facteur seul ou des facteurs combinés
(interactions). Cette fonction est donc déterministe (la réponse
dépend uniquement des facteurs sans aucune incertitude possible, ce
qui revient à ignorer les bruits tels que les erreurs de mesure) et
invariant (le comportement n'évolue pas au cours du temps).
Une méthode classique d'étude consiste en la mesure de la réponse y pour
plusieurs valeurs de la variable 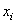 tout
en laissant fixe la valeur des (n-1) autres variables. Nous itérons
alors cette méthode pour chacune des variables. tout
en laissant fixe la valeur des (n-1) autres variables. Nous itérons
alors cette méthode pour chacune des variables.
Ainsi, par exemple, si nous avons 8 variables et si l'on décide de donner
2 valeurs expérimentales à chacune d'elles, nous sommes conduits à effectuer 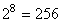 expériences. expériences.
Ce nombre élevé dépasse les limites de faisabilité tant en temps qu'en coût.
Il faut donc réduire le nombre d'expériences à effectuer sans pour autant perdre
sur la qualité des résultats recherchés.
L'utilisation d'un plan d'expérience donne alors une stratégie dans le choix
des méthodes d'expérimentation. Le succès des plans d'expériences dans la recherche
et l'industrie est lié au besoin de compétitivité des entreprises : ils permettent
une amélioration de la qualité et une réduction des coûts.
Remarque: La méthode des plans d'expériences a été mise au point au début
du siècle, dans les années 1920, par Ronald A. Fisher (celui du Test de Fisher).
Elle a pris un essor considérable avec le développement de l'informatique et
la puissance de calcul qui l'accompagne.
Le traitement des résultats se fait enfin à l'aide de la régression linéaire
multiple et l'analyse de variance.
Avec les plans d'expériences, le but est donc d'obtenir le maximum de renseignements
(mais pas tous!) avec le minimum d'expériences (et donc le minimum de coût).
Un expérimentateur qui lance une étude s'intéresse à une grandeur qu'il mesure à chaque
essai. Cette grandeur s'appelle la "réponse", c'est la grandeur d'intérêt.
La valeur de cette grandeur dépend de plusieurs variables. Au lieu du terme "variable" on
utilisera le mot "facteur". La valeur donnée à un facteur pour réaliser
un essai est appelée "niveau". Lorsqu'on étudie l'influence d'un
facteur, en général, on limite ses variations entre deux bornes (oui faut bien
s'avoir s'arrêter un jour et être raisonnable...) appelées respectivement: "niveau
bas" et "niveau haut".
Bien évidemment, lorsque nous avons plusieurs facteurs 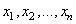 ceux-ci
représentent un point dans ceux-ci
représentent un point dans 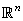 appelé alors "espace
expérimental". appelé alors "espace
expérimental".
L'ensemble de toutes les valeurs que peut prendre le facteur entre le niveau
bas et le niveau haut, s'appelle le "domaine de
variation du facteur" ou
plus simplement le "domaine du facteur".
Nous avons l'habitude de noter le niveau bas par -1 et le niveau haut par +1
pour des raisons d'approximation
de mathématiques car l'approche utilise un développement en série
de MacLaurin autour de zéro! Ce n'est donc pas une recommandation de
procéder ainsi mais
une obligation car les logiciels implémentent les séries de MacLaurin!
Donc par exemple pour un facteur ayant un domaine de variation compris entre
un niveau haut de 20 [°C] correspond à +1 et un niveau bas de 5 [°C] correspondant à -1
nous devrons à la fin de notre étude transformer toutes les valeurs
expérimentales
en "unités centrées réduites" dans
lesquelles doivent être utilisées
les 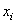 . .
Ainsi, nous avons deux points d'entrée (20,5) et deux de sorties
(+1,-1). Toute valeur intermédiaire est donnée simplement par
l'équation
de la droite:

(240)
La pente est donc triviale à obtenir...., pour déterminer b, nous avons
simplement une équation à une inconnue:
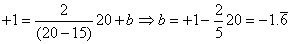 (241)
(241)
ou (ce qui revient au même):
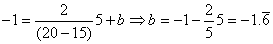 (242)
(242)
Donc le passage de variables non normalisées, notées x, aux normalisé,
notées X, s'écrit alors:
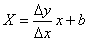 (243)
(243)
soit dans un cas de sorties (+1,-1):
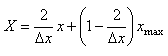 (244)
(244)
et inversement...:
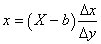 (245)
(245)
soit dans un cas de sorties (+1,-1):
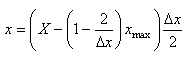 (246)
(246)
Le regroupement des domaines de tous les facteurs définit le "domaine
d'étude". Ce domaine d'étude est la zone de l'espace expérimental choisie
par l'expérimentateur pour faire ses essais. Une étude, c'est-à-dire plusieurs
expériences bien définies, est représentée par des points répartis dans le
domaine d'étude.
Par exemple, pour deux facteurs, le domaine d'étude est une surface et l'espace
expérimental est 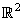 : :

(247)
Les niveaux 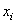 représentent
les coordonnées d'un point expérimental et y est la valeur de la réponse
en ce point. On définit un axe orthogonal à l'espace expérimental et on l'attribue à la
réponse. La représentation géométrique du plan d'expériences et de la réponse
nécessite un espace ayant une dimension de plus que l'espace expérimental.
Un plan à deux facteurs utilise un espace à trois dimensions pour être représenté :
une dimension pour la réponse, deux dimensions pour les facteurs. représentent
les coordonnées d'un point expérimental et y est la valeur de la réponse
en ce point. On définit un axe orthogonal à l'espace expérimental et on l'attribue à la
réponse. La représentation géométrique du plan d'expériences et de la réponse
nécessite un espace ayant une dimension de plus que l'espace expérimental.
Un plan à deux facteurs utilise un espace à trois dimensions pour être représenté :
une dimension pour la réponse, deux dimensions pour les facteurs.
A chaque point du domaine d'étude correspond une réponse. A
l'ensemble de tous les points du domaine d'étude correspond un ensemble
de réponses qui se
localisent sur une surface appelée la "surface
de réponse" (raison pour laquelle ce domaien d'études est
parfois appelé: "plans d'expérience pour l'estimation de surfaces de réponse")
par exemple avec des facteurs:

(248)
Le nombre et de l'emplacement des points d'expériences est le problème
fondamental des plans d'expériences. On cherche à obtenir la meilleure
précision possible
sur la surface de réponse tout en limitant le nombre d'expériences!
L'ingénieur va souvent rechercher une fonction mathématique qui relie la
réponse aux facteurs.
Pour cela, nous simplifions le problème en se rappelant (cf.
chapitre de Suites et Séries) que toute fonction quelque soit sont nombre de variables
peut être approchée en une somme de série de puissance en un point donné
Nous prenons alors un développement limité de la série
de Taylor: 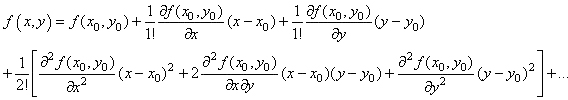 (249)
(249)
Soit autour de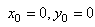 (ce
que nous pouvons nous permettre car nous prenons toujours des unités
centrées
réduites comme vues plus haut!),
nous avons la série de MacLaurin au deuxième ordre et en changeant
de notation pour (ce
que nous pouvons nous permettre car nous prenons toujours des unités
centrées
réduites comme vues plus haut!),
nous avons la série de MacLaurin au deuxième ordre et en changeant
de notation pour 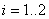 : :

(250)
où y est donc la réponse et les 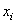 les
facteurs et les les
facteurs et les 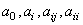 sont
les coefficients du modèle mathématique adopté a priori. Ils ne sont pas connus
et doivent être calculés à partir des résultats des expériences. sont
les coefficients du modèle mathématique adopté a priori. Ils ne sont pas connus
et doivent être calculés à partir des résultats des expériences.
L'intérêt de modéliser la réponse par un polynôme est de pouvoir calculer
ensuite toutes les réponses du domaine d'étude sans être obligé de faire les
expériences en passant par un modèle appelé "modèle
postulé" ou "modèle
a priori".
Deux compléments doivent être apportés au modèle précédemment décrit:
1. Le
premier complément est le "manque d'ajustement".
Cette expression traduit le fait que le modèle a priori est fort probablement
différent (ne
serait-ce que par l'approximation de l'approche) du modèle réel qui régit le
phénomène étudié. Il y a un écart entre ces deux modèles. Cet écart est le
manque d'ajustement ("lack of fit" en anglais).
2. Le second complément est la prise en compte de la nature aléatoire de
la réponse (sans que cette dernière soit toutefois stochastique sinon il faut
utiliser d'autres outils!). En effet, si l'on mesure plusieurs fois une réponse
en un même
point expérimental, on n'obtient pas exactement le même résultat. Les résultats
sont dispersés. Les dispersions ainsi constatées sont appelées "erreurs
expérimentales".
Ces deux écarts, manque d'ajustement et erreur expérimentale, sont souvent
réunis dans un seul écart, notée e.
Le modèle utilisé par l'expérimentateur
s'écrit alors au deuxième ordre et au premier degré (toujours dans le cas particulier
de deux facteurs!): 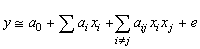 (251)
(251)
Remarques:
R1. Si nous prenons en compte les termes
du deuxième degré, nous parlons
alors de "modèle quadratique complet".
R2. Si nous arrêtons le développement au premier ordre et au premier degré
(sans interactions), nous parlons alors de "modèle
affine".
Dans la pratique nous notons cette dernière relation (nous enlevons
le terme d'erreur):
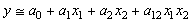 (252)
(252)
où nous avons la notation abusive:
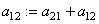 (253)
(253)
Ce modèle sans erreur est souvent appelé "modèle
contrôlé avec interactions" (linéaire d'ordre
2).
Évidemment, plus le degré du polynôme utilisé est élevé plus
nous avons, théoriquement, de chances d'avoir un modèle proche
de la réalité. Mais les polynômes de degré élevé réclament
beaucoup de points expérimentaux et leur validité peut vite diverger
en dehors du domaine expérimental. Si l'étude l'exige, nous préférons
utiliser des fonctions mathématiques particulières pour mieux
ajuster le modèle aux résultats expérimentaux.
Cependant, en pratique, les interactions d'ordre élevé ont
souvent une influence très faible sur la réponse (bon cette affirmation
dépend fortement du domaine d'activité...!). Il est donc possible
de ne pas les inclure dans le modèle,
ce qui conduit à faire
moins d'essais. Ce principe est utilisé dans la construction de nombreux
plans d'expériences, comme nous le verrons dans la partie suivante.
Dans de nombreuses applications, on obtient des résultats tout à fait
satisfaisants en se limitant aux interactions doubles.
Pourquoi nous satisfaisons-nous de cette relation approchée de quatre termes?
Pour la simple raison que:
1. La réponse peut être non nulle lorsque tous les facteurs sont nuls (c'est
le premier coefficient 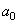 ) )
2. La réponse dépend trivialement (intuitivement) de la somme des effets
du premier et deuxième facteurs 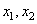 de
manière indépendante (coefficients de
manière indépendante (coefficients 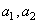 ). ).
3. La réponse dépend aussi des interactions entre les deux facteurs 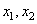 (coefficients (coefficients 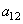 ). ).
Chaque point expérimental dont les 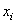 sont
données permet alors d'obtenir une valeur de la réponse y. Cette
réponse est modélisée par un polynôme dont les coefficients sont les inconnues
qu'il faut déterminer. sont
données permet alors d'obtenir une valeur de la réponse y. Cette
réponse est modélisée par un polynôme dont les coefficients sont les inconnues
qu'il faut déterminer.
PLANS FACTORIELS COMPLETS
Donc dans un plan d'expérience de 2 facteurs à 2 niveaux, nous avons besoin
d'au moins (et au plus pour des raisons de coûts!) de 4 mesures pour avoir
un système
de quatre équations à quatre inconnues qui sont les coefficients 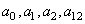 . .
Remarque:
Pour une étude de 2 facteurs à 3 niveaux, nous ne pouvons plus prendre le modèle
linéaire. Il nous faut alors prendre les termes quadratiques du développement
de Taylor.
Dans la pratique, puisque pour chacun des facteurs nous devons nous fixer
un niveau bas et un niveau haut pour pouvoir travailler raisonnablement.... alors
si nous avons deux facteurs, nous avons un espace expérimental défini par 4
points {(haut, haut), (bas, bas), (haut, bas), (bas,haut)}, correspondant aux
2 fois 2 niveaux ( ),
nous suffit pour permettre d'obtenir alors nos quatre équations à 4 inconnues
et alors de déterminer les 4 coefficients. ),
nous suffit pour permettre d'obtenir alors nos quatre équations à 4 inconnues
et alors de déterminer les 4 coefficients.
Ainsi, les points à prendre pour notre expérience correspondent naturellement
aux sommets (géométriquement parlant) de l'espace expérimental.
Nous avons alors le système d'équations:
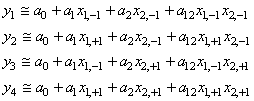 (254)
(254)
ou explicitement écrit:
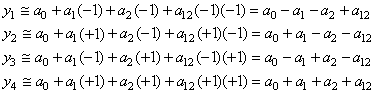 (255)
(255)
Il vient alors immédiatement ce que les ingénieurs dans le domaine, appellent
les "effets moyens", des différents facteurs:
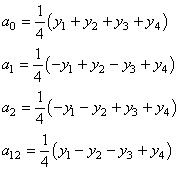 (256)
(256)
où 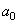 a
un statut particulier car il représente la réponse théorique moyenne (au centre
du domaine d'étude). a
un statut particulier car il représente la réponse théorique moyenne (au centre
du domaine d'étude).
Effectivement, si nous posons dans une ligne quelconque:
(257)
soit au centre du domaine [+1,-1] de chaque variable alors nous obtenons
tout naturellement:
(258)
qui est donc la réponse de l'expérience au centre du domaine d'étude.
Soit sous forme matricielle:
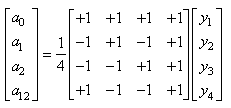 (259)
(259)
Ce qui s'écrit de manière générale pour des modèles linéaires du deuxième
ordre sous la forme générale (cf. chapitre d'Algèbre Linéaire):
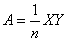 (260)
(260)
La matrice X contenant 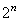 lignes
est appelé "plan factoriel complet (PFC) 2n avec
interactions" (le
terme "factoriel" venant du fait que tous les facteurs varient simultanément). lignes
est appelé "plan factoriel complet (PFC) 2n avec
interactions" (le
terme "factoriel" venant du fait que tous les facteurs varient simultanément).
La matrice X dans la pratique est appelée "matrice
d'expérimentation" ou
encore "matrice des effets" et est souvent représentée de la manière
suivante dans le cas particulier précédent:
Essai
n° |
Repos |
Facteur
1 |
Facteur
2 |
Facteur
12 |
Réponse |
1 |
+1 |
-1 |
-1 |
+1 |

|
2 |
+1 |
+1 |
-1 |
-1 |

|
3 |
+1 |
-1 |
+1 |
-1 |

|
4 |
+1 |
+1 |
+1 |
+1 |

|
Tableau: 13
- Matrice d'expérimentation
Mais l'on voit tout de suite que dans la pratique la deuxième colonne (Repos)
est inutile car elle vaut toujours +1 et elle est implémentée de manière cachée
dans les logiciels.
Il en est de même pour la cinquième colonne (Facteur 12) car elle
se déduit automatiquement de la troisième et quatrième colonne (c'est la multiplication
des termes ligne par ligne... ce que certains appellent la "multiplication
de Box").
Remarque: Observez donc que la première colonne vaut toujours +1 et il y
a toujours aussi une ligne avec uniquement des +1!
Ainsi, dans la pratique (logiciels) et dans de nombreux ouvrages on représente à juste
titre uniquement le tableau suivant (ce qui masque le fait que nous avons affaire à une
matrice carrée):
Essai
n° |
Facteur
1 |
Facteur
2 |
Réponse |
1 |
-1 |
-1 |

|
2 |
+1 |
-1 |

|
3 |
-1 |
+1 |

|
4 |
+1 |
+1 |

|
Tableau: 14
- Matrice d'expérimentation simplifiée
pour un plan d'expérience de 2 facteurs à 2 niveaux avec interactions
en modèle
linéaire (sans erreur) ou encore plus extrême ("notation
de Yates")... en
termes d'écriture:
Essai
n° |
Facteur
1 |
Facteur
2 |
Réponse |
1 |
- |
- |

|
2 |
+ |
- |

|
3 |
- |
+ |

|
4 |
+ |
+ |

|
Tableau: 15
- Matrice d'expérimentation avec notation de Yates
On voit que dans cette forme d'écriture qu'outre le fait que les deux
colonnes Facteur 1
et Facteur 2 sont orthogonales, elles sont aussi "balancées",
dans le sens qu'il y a autant de + et de - dans chacune des colonnes.
Lorsque le nombre de facteurs est grand, il n'est pas toujours facile pour
tout le monde de poser rapidement les facteurs +, -. Alors il existe une petite
marche à suivre appelée "algorithme de Yates" qui permet vite d'arriver
au résultat voulu:
D'abord nous commençons toutes les colonnes par -1 et nous alternons les
-1 et les +1 toutes les 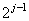 lignes
pour la j-ème colonne. lignes
pour la j-ème colonne.
Remarques:
R1. Si le type de tableau précédent contient des valeurs codées, nous parlons
de "plan d'expérience" sinon avec les unités physiques habituelles
nous parlons de "tableau d'expérimentation".
R2. Dans le cas des tableaux codés, il est d'usage d'indiquer sous le tableau
un deuxième tableau avec les correspondances entre les unités codées et les
unités physiques.
Insistons sur une chose importante: C'est que si nous avions 3 facteurs à 2
niveaux, alors nous avons  possibilités
d'expériences (soit 8). Or, huit correspond exactement au nombre de
coefficients que nous avons également dans le modèle linéaire
avec interactions d'une réponse à trois
variables: possibilités
d'expériences (soit 8). Or, huit correspond exactement au nombre de
coefficients que nous avons également dans le modèle linéaire
avec interactions d'une réponse à trois
variables:
 (261)
(261)
ce qui correspond aussi aux termes seulement linéaires et sous forme condensée
du développement en série de MacLaurin d'une fonction f de trois variables.
Et ainsi de suite.... pour n facteurs à deux niveaux. C'est la raison
pour laquelle les plans factoriels complets linéaires 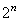 sont
traditionnellement les plus utilisés car ils sont mathématiquement intuitifs
et simples à démontrer. sont
traditionnellement les plus utilisés car ils sont mathématiquement intuitifs
et simples à démontrer.
Par ailleurs, il est important de remarquer que tous ces plans linéaires
complets approximés au deuxième ordre sont sous forme matricielles des matrices
carrées 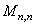 orthogonales
et donc bien évidemment inversibles (cf. chapitre d'Algèbre Linéaire)! orthogonales
et donc bien évidemment inversibles (cf. chapitre d'Algèbre Linéaire)!
Cependant les matrices précédentes ne satisfont pas la relation suivante
vue dans le chapitre d'Algèbre Linéaire:
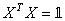 (262)
(262)
mais ont pour particularité pour tout plan d'expérience complet de satisfaire
la relation:
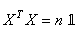 (263)
(263)
Donc contrairement aux matrices orthogonales qui par définition ont toutes
les colonnes (ou lignes) qui forment une base orthonormée (norme unitaire),
les matrices des plans d'expérience ont pour différence de ne pas avoir les
normes de la base orthogonale à l'unité.
Ainsi, nous définissons la matrices A dont les coefficients sont tous
des +1 ou des -1 ET satisfaisant la relation précédente comme étant une "matrice
de Hadamard". Ces dernières ont par ailleurs pour propriété d'exister
que pour les ordres 1, 2, 4, 8, 12, 16, 20, 24, ...
Démonstration:
Sachant que les cas d'ordre 1 et 2 sont triviaux et que le cas impair est à éliminer
immédiatement (impossibilité d'orthogonalité), faisons la démonstration pour 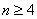 .
Puisque toutes les colonnes doivent être obligatoirement orthogonales (pour
que la matrice soit inversible et donc le système résoluble), nous pouvons
toujours écrire le problème sous la forme (forme particulière pour n valant
4 mais facilement généralisable): .
Puisque toutes les colonnes doivent être obligatoirement orthogonales (pour
que la matrice soit inversible et donc le système résoluble), nous pouvons
toujours écrire le problème sous la forme (forme particulière pour n valant
4 mais facilement généralisable):
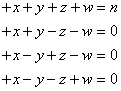 (264)
(264)
et si nous notons m comme étant l'ordre de la matrice. Alors nous
avons par sommation de toutes les lignes:
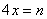 (265)
(265)
donc n doit être divisible par 4 pour 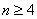 pour
que toutes les colonnes soient orthogonales et donc que la matrice soit de
Hadamard sachant que x, y, z, w ont pour valeur
1. pour
que toutes les colonnes soient orthogonales et donc que la matrice soit de
Hadamard sachant que x, y, z, w ont pour valeur
1.
Remarque: Nous pouvons donc avoir des matrices par exemple d'ordre 4, avec
des coefficients +1 ou -1 mais qui ne sont pas des matrices de Hadamard (car
les colonnes ne seraient pas orthogonales).
 C.Q.F.D. C.Q.F.D.
Il s'ensuit alors trivialement la relation suivante:
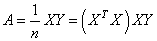 (266)
(266)
Pour clore cette partie, résumons un constat simple:
Plan |
Facteurs |
Interactions |
Somme |

|
2 |
1 |
3 |

|
3 |
4 |
7 |

|
4 |
11 |
15 |

|
5 |
26 |
31 |

|
6 |
57 |
63 |

|
7 |
120 |
127 |
... |
... |
... |
... |
Tableau: 16
- Types de plans avec facteurs & interactions
PLANS FACTORIELS FRACTIONNAIRES
En pratique, les plans complets ne sont utilisables que sur des systèmes
avec très peu de facteurs, ou lorsque chaque essai prend très
peu de temps. Lorsque n est plus grand ou égal 3 alors les coûts
des expériences
peut très vite devenir onéreux.
Dans le cas de 3 facteurs à 2 niveaux nous avons l'équation
et le tableau d'expérience
suivant:

Essai
n° |
Facteur
1 |
Facteur
2 |
Facteur
3 |
Réponse |
1 |
- |
- |
- |

|
2 |
+ |
- |
- |

|
3 |
- |
+ |
- |

|
4 |
+ |
+ |
- |

|
5 |
- |
- |
+ |

|
6 |
+ |
- |
+ |

|
7 |
- |
+ |
+ |

|
8 |
+ |
+ |
+ |

|
Tableau: 17
- Plan d'expérience à 3 facteurs complet sous forme de Yates
Soit sous forme de tableau d'expérience complet:
Essai
n° |
Repos |
F 1 |
F 2 |
F 3 |
F 12 |
F 13 |
F 23 |
F 123 |
Réponse |
1 |
+ |
- |
- |
- |
+ |
+ |
+ |
- |

|
2 |
+ |
+ |
- |
- |
- |
- |
+ |
+ |

|
3 |
+ |
- |
+ |
- |
- |
+ |
- |
+ |

|
4 |
+ |
+ |
+ |
- |
+ |
- |
- |
- |

|
5 |
+ |
- |
- |
+ |
+ |
- |
- |
+ |

|
6 |
+ |
+ |
- |
+ |
- |
+ |
- |
- |

|
7 |
+ |
- |
+ |
+ |
- |
- |
+ |
- |

|
8 |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |

|
Tableau: 18
- Plan d'expérience à 3 facteurs et interactions complet sous
forme
de
Yates
ou de matrice d'expérience complète:
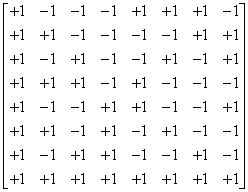 (267)
(267)
où à nouveau il est facile de contrôler que toutes les colonnes sont orthogonales
et balancées (même nombre de + ou de - dans chaque colonne ou autrement
dit la somme de leurs colonnes est nulle) et que la matrice est bien de type
Hadamard.
Les plans réduits (plans factoriels fractionnaires), consistant à sélectionner
certaines combinaisons, ont donc été proposés. Ils permettent
naturellement de réduire les coûts mais diminuent également
l'information disponible sur le comportement du système ; il faut donc
s'assurer de la pertinence de la sélection par rapport au modèle à identifier.
Pour réduire les coûts d'expérimentation nous allons jouer avec les maths.
D'abord reprenons le problème actuel sous forme explicite:
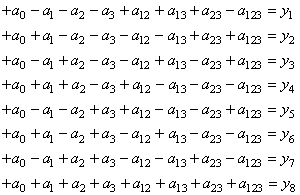 (268)
(268)
Pouvons-nous en réduire l'écriture afin de minimiser le nombre d'expériences à faire?
La réponse est Oui mais en contre partie nous allons perdre la mesure des effets
purs (nous parlons alors parfois de "confusion").
L'écriture inférieure la plus proche est une matrice de Hadamard d'ordre
4. Ce qui signifie bien évidemment que nous ne devons conserver 4 lignes sur
les 8 et que celles-ci doivent rester orthogonales, balancées et satisfaire
la relation:
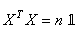 (269)
(269)
L'idée est alors dans un premier temps de rassembler les facteurs d'influence
(en indices) tel que (développements similaires pour tout n):
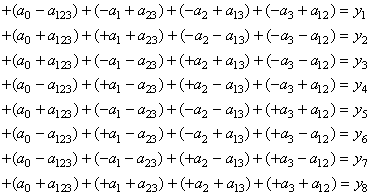 (270)
(270)
Ecrivons cela de la manière suivante:
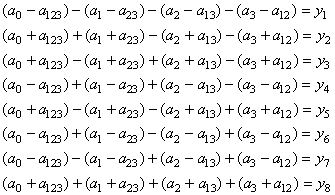 (271)
(271)
Changeons de notation:
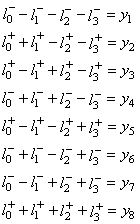 (272)
(272)
Tout naturellement, si nous considérons cette nouvelle notation comme des
variables propres, ce système unique se sépare maintenant en deux sous-systèmes
(appelés respectivement "contrastes" dans le domaine) pour être résoluble:
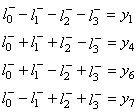 et et 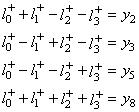 (273)
(273)
En résolvant un de ces deux systèmes, nous disons que les interactions sont "aliasées" avec
les effets purs en négatif ou en positif.
Il est ensuite de tradition de garder que le système aliasé positivement:
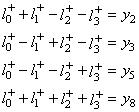 (274)
(274)
car si les interactions sont nulles, nous retrouvons à l'identique la matrice
d'expérience d'un plan factoriel complet  ! !
Remarque: Il
est même intéressant d'observer que le troisième facteur est
confondu (peut être assimilé) avec l'interaction 12 des facteurs 1 et 2 dans
le plan factoriel  .
Ensuite, c'est à l'expérimentateur de bien connaître son analyse et de savoir
si:
1. Parmi les facteurs aliasés s'il y a des interactions ou non!
2. Dans le facteur aliasé l'influence forte sur la réponse vient de l'interaction
ou de l'effet pur seul!
Une fois les coefficients déterminés, sous l'hypothèse que chacun des facteurs
ou interactions est indépendant (hypothèse limite acceptable...) certains ingénieurs
font une analyse de la variance de la droite de régression obtenue au final
ou déterminent le coefficient de corrélation afin de déterminer si l'approximation
linéaire du modèle est acceptable dans le domaine d'étude et d'application.
Enfin signalons qu'il semblerait que les ingénieurs désignent
(à vérifier car je ne suis pas un spécialiste):
- les plans factoriels où aucune interaction est prise en compte dans
le modèle à priori linéaire sous le nom de "plans
Plackett et Burmann" (mais ces plans peuvent cacher des alias si
l'expérience
est mal connue).
- les plans factoriels avec interactions dans le modèle à priori linéaire
construits à l'aide de graphes linéaires (cf.
chapite de Théorie des Graphes) sous le nom de "plans
de Taguchi" (au fait il s'agit
simplement de plans factoriels complets ou fractionnaires construits avec l'aide
de graphes).
- les plans factoriels avec interactions dans le modèle à priori non linéaire
de degré n sous le nom de "plans
de Koshal".
Un aspect mérite encore d'être précisé: c'est la vérification
de la validité du modèle mathématique du premier degré.
Or aucun de ces plans ne prévoit un tel test de validité utilisant
des statistiques élaborées. C'est pourquoi il est préconisé de
toujours ajouter au moins un point expérimental au contre du domaine
expérimental. La valeur de la réponse en ce point sera comparée à la
valeur déduite des autres points expérimentaux grâce au
modèle mathématique. Si les deux valeurs sont semblables, le
modèle mathématique sera adopté, si elles ne le sont pas
nous devrons rejeter ce modèle et compléter les résultats
déjà obtenus par des expériences permettant de passer
au second degré.
|