|

DYNAMIQUE DES POPULATIONS | THÉORIE
DES JEUX ET DE LA DÉCISION | ÉCONOMIE
TECHNIQUES DE GESTION | MUSIQUE MATHÉMATIQUE
| 67.
TECHNIQUES DE GESTION |
Dernière mise à jour de ce chapitre:
2017-02-23 23:34:35 | {oUUID 1.807}
Version: 3.2 Révision 32 |
Avancement:
~85%
 vues
depuis
le 2012-01-01:
9'931 vues
depuis
le 2012-01-01:
9'931
 LISTE DES SUJETS TRAITÉS SUR CETTE PAGE
LISTE DES SUJETS TRAITÉS SUR CETTE PAGE
L'objectif
de ce chapitre est d'introduire les principales techniques mathématiques
de production et de gestion, de maintenance et de qualité dont
l'utilisation est devenue indispensable aux ingénieurs,
gestionnaires et cadres des entreprises modernes (ceux qui le
peuvent font de la science, les autres de la méthodologie...)
et qui constituent le minimum-minimorum de la connaissance du
métier
de la gestion en général. Ce sont des techniques
qui datent du début du 20ème siècle et qui ont d'abord été utilisées
par l'armée américaine pour la majorité pour ensuite se voir petit
à petit implémentées dans les plus grandes entreprises mondiales.
Par ailleurs, c'est un
excellent chapitre pour la culture générale
du physicien ou du mathématicien...
et un acquis pour l'ingénieur!
Beaucoup de techniques ne seront cependant pas présentées
ici car ayant déjà été démontrées
dans d'autres chapitres du site. Effectivement, les techniques
de gestion complexes et critiques font un
énorme usage des statistiques et probabilités, de
la théorie
de la décision, de la théorie des graphes (chaînes
de Markov ou non, graphes complets pour la gestion de la communication),
de l'analyse financière
et des algorithmes d'optimisation.
Des
chapitres
entiers
y étant déjà consacrés sur ce site,
il serait redondant d'y revenir!
Remarque: Nous
parlons souvent de 3M (Méthodes Mathématiques de
Management) ou chez les anglophones de "scientific management"
pour décrire
l'ensemble des outils mathématiques appliqués à la
gestion (il existe d'ailleurs un cursus de formation continue
à ce sujet d'une cinquantaine de jours) ou encore de SciProM
pour "Scientific Project Management). Un terme anglophone
courant et qui devient à la
mode en Europe pour décrire ce domaine d'application est
aussi le "decisioneering" faisant
référence au fait que ce sont des outils d'aide à la
décision pour les ingénieurs.
Indiquons avant de commencer que malgré leur importance
intrinsèque, les techniques quantitatives de gestion (incluant
aussi les techniques de recherche opérationnelle, modélisation
par Monte-Carlo et le Bootstrapping vues dans le chapitre d'Informatique
Théorique
ainsi que Six Sigma vu dans le chapitre de Génie Industriel
et la Théorie de la Décision) sont encore peu utilisées
dans le monde industriel, soit à cause
du manque de formation des décideurs (excepté dans
le domaine de la finance), soit par le manque de pertinence de
l'outil
ou sa difficulté de
mise en œuvre.
Les principales craintes émises par les décideurs
quant à l'application
de modèles mathématiques dans l'entreprise sont:
1. Les outils sont trop abstraits: Dans cette situation, je rappelle
toujours que le concret, c'est de l'abstrait auquel on est habitué!
2. Une prise en compte limitée des facteurs:
Pour les questions stratégiques, la réponse pure
et parfaite d'une solution mathématique semble rarement
applicable de facto. Même si les techniques quantitatives
intègrent beaucoup de facteurs, si certains aspects sont
relativement faciles à modéliser au sens mathématique
du terme (le coût, la rentabilité, la distance, la
durée,
la cadence, par exemple), d'autres éléments sont
en revanche plus difficiles à modéliser: contraintes
légales, volonté commerciale de faire barrage à un
concurrent, importance des relations avec les élus, climat
social, etc. Le poids de ces éléments dans la décision
est pourtant important, parfois déterminant.
3. Un investissement
important:
L'outil mathématique lui-même exige un niveau élevé de
connaissances mathématiques, une bonne aptitude à modéliser
les problèmes et décrire les facteurs. Ces contraintes
sont consommatrices de beaucoup de temps et d'une certaine somme
d'argent (que ce soit par développement
interne, qui consomme des ressources - ou par développement
externe, qui consomme de l'argent). Il est alors nécessaire
de trouver un équilibre entre l'investissement nécessaire
et les retombées prévues.
4. Pour des événements
peu fréquents:
L'entreprise ne bénéficie pas de l'effet d'expérience
et donc d'une fois sur l'autre, le problème concerne un
service différent, ou les responsables ont changé entre
deux études.
Il est donc difficile d'entretenir les compétences à l'intérieur
de l'entreprise. Le décideur devra prendre ces différents
aspects en compte lorsqu'il décidera ou non de mettre en œuvre
des techniques quantitatives dans son
entreprise.
Nous pouvons aussi argumenter que ce qui fait que
les techniques scientifiques de gestion (TQG) ou les méthodes
mathématiques de management (3M) ne sont guère
répandues est que:
1. Dans un environnement peu exigeant le surcroît de puissance
qu'offrent les TQG/3M ne justifie pas forcément les efforts
nécessaires à leur apprentissage.
2. Les TQG/3M sont exigeantes en raisonnements et rigoureuses,
elles ne peuvent donc convenir aux personnes qui ne connaissent
ni les
uns ni les autres...
Remarque: Méfiez-vous des entreprises
- particulièrement des multinationales - qui recherchent
des spécialistes en gestion de projets ou en logistique
maîtrisant
Microsoft Excel, Microsoft Access ou VBA. Car cela signifiera
qu'elles utilisent des outils non professionnels
pour faire un travail qui lui devrait pourtant l'être avec
des outils adaptés (et Microsoft Excel ou Microsoft Access
ne le sont pas!!!). Donc en termes d'organisation interne, vous
pouvez
vous assurer
que
ces
entreprises
organisent
et analysent
n'importe
quoi,
n'importe
comment, avec un outil non adapté et donc que c'est le bordel
général en interne.
Nous avons choisi dans cette section de présenter les techniques
quantitatives de gestion les plus classiques dans un ordre croissant
de difficulté
(niveau de technicité). Cela nous semble à ce jour
le choix pédagogique
le plus pertinent.
Donnons un résumé schématique de la méthode
scientifique vue dans le chapitre d'Introduction et qui s'applique
assez bien au
niveau du monde des affaires en ce qui concerne le management scientifique:

Figure: 67.1 - Processus simplifié type
Les sujets simples sont donnés sans exemples pratiques alors que
ceux qui dépassent le niveau de l'école obligatoire sont accompagnés
d'exemples pratiques plus ou moins détaillés.
ANALYSE DU SEUIL DE RENTABILITÉ (POINT MORT)
L'analyse du seuil de rentabilité ("break-even analysis" en
anglais), appelé aussi "analyse du point
mort", est l'ensemble
des calculs permettant de déterminer le niveau d'activité minimum à partir
duquel une organisation devient rentable pour elle-même par ses économies
d'échelle, c'est-à-dire qu'elle cesse de perdre de l'argent sur
cette activité. Évidemment, cette technique permet aussi de comparer
plusieurs stratégies entre elles.
Le "point mort" est donc assez
intuitivement le point d'intersection entre la courbe du chiffre
d'affaires (car le chiffre d'affaires
est normalement une fonction de plusieurs variables) et la courbe
des charges (elle aussi une fonction de plusieurs variables) nécessaires
pour produire ce chiffre d'affaires. En d'autres termes, il s'agit
des coordonnées correspondantes à l'égalité des deux fonctions
(dans la pratique on le représente rarement graphiquement car les
variables sont trop nombreuses).
Normalement cette technique doit permettre à un gestionnaire de
déterminer des informations comme:
- Prédire le volume de ventes pour couvrir tout juste les coûts
(point mort)
- Quel doit être le prix par unité pour couvrir tout juste les
coûts
(point mort)
- Quel est le niveau des coûts fixes qui équilibre tout juste
les gains (point mort)
- Comment les prix influent sur le volume de ventes correspondant à l'équilibre
(point mort)
L'analyse du point mot est basée sur l'hypothèse que tous les
coûts relatifs à la fabrication d'un bien peuvent être divisés
en deux catégories: coûts variables et coûts fixes.
Le coût total  est
défini par la relation: est
défini par la relation:
 (67.1)
(67.1)
où F représente les coûts fixes, c le coût par unité (supposé indépendant
de la quantité) de biens produits et Q la quantité correspondante.
L'hypothèse que le coût par unité soit indépendant de la quantité permet
de simplifier le calcul pour avoir le coût total qui est une
simple fonction linéaire, mais cette hypothèse n'est plus vraiment
nécessaire aujourd'hui avec les tableurs.
Si nous supposons que toutes les unités produites sont vendues,
le revenu total  est
défini par: est
défini par:
 (67.2)
(67.2)
où p est le revenu par unité vendue.
Le point mort est alors l'égalité entre les deux coûts, ce qui
signifie:
 (67.3)
(67.3)
Ainsi, nous pourrions alors par exemple après quelques opérations
algébriques élémentaires, déterminer la quantité qui permet
d'arriver au point mort:
 (67.4)
(67.4)
Ainsi, connaissant F (coûts fixes), p (revenus par
unité produite) et c (coûts par unité produite), il
est possible de déterminer la quantité Q à vendre
pour arriver au point mort.
Signalons qu'un sujet qui intéresse beaucoup les gestionnaires
c'est l'étude de la variation de certains paramètres en fonction
des autres variables. Nous appelons cela "l'analyse
de la sensibilité" dans le cas multivarié (analyse
se basant sur le coefficient de corrélation Pearson) et "l'analyse
par double entrée" dans le cas bivarié. Évidemment
dans le cas linéaire,
cette analyse est assez triviale.
Remarques: Depuis le début des années
1980, il existe des logiciels très simples à utiliser comme @Risk
de Palisade permettant de faire des simulations de Monte-Carlo
pour déterminer
le point-mort probabiliste et ce même
avec des solveurs qui permettent de résoudre des systèmes non linéaires
et faire de l'analyse de la sensibilité très poussée. Sinon pour
une analyse scolaire, un tableur suffit...
DIAGRAMME DE PARETO
Le diagramme de Pareto, comme nous allons le voir, est un moyen
(parmi d'autres) simple pour classer les phénomènes
par ordre d'importance. Mais la distribution de Pareto est aussi
souvent utilisée en entreprise comme base de simulation
stochastique pour des variables aléatoires représentant
des investissements chiffrés de projets (à peu
près
aussi souvent utilisée que la distribution triangulaire,
la distribution Bêta ou log-Normale dans l'industrie moderne).
Rappelons alors qu'une variable
aléatoire
est dite par définition suivre une loi de Pareto si
sa fonction de répartition est donnée par (cf.
chapitre de Statistiques):
 (67.5)
(67.5)
avec  et et  (donc (donc  )
et pour l'espérance (moyenne): )
et pour l'espérance (moyenne):
 (67.6) (67.6)et la variance:
 (67.7)
(67.7)
Pour illustrer ce type de
représentation, nous supposerons qu'une étude de
réorganisation
du réseau commercial de l'entreprise LAMBDA conduise le
directeur commercial à s'intéresser à la
répartition
des 55'074 bons de commande (valeur en bas à droite du tableau)
reçus
pendant une année donnée selon la ville où sont
domiciliés
les clients (nous avons retenu ici les 200 premières villes
du pays imaginaire d'où les 200 lignes réparties
en 5 colonnes).
Pour calculer les paramètres de la loi de Pareto, le lecteur
devra se reporter au chapitre de Génie Industriel, car nous
n'allons ici avoir qu'une approche qualitative comme le font les
gestionnaires,
l'analyse quantitative étant réservée majoritairement
aux ingénieurs.
Ces données
sont reproduites dans le tableau ci-dessous:
ni |
Ni |
ni |
Ni |
ni |
Ni |
ni |
Ni |
ni |
Ni |
8965 |
8965 |
240 |
40027 |
125 |
46378 |
88 |
50916 |
55 |
53752 |
4555 |
13520 |
236 |
40263 |
124 |
46862 |
87 |
51003 |
54 |
53806 |
3069 |
16589 |
224 |
40487 |
123 |
46985 |
87 |
51090 |
54 |
53860 |
2336 |
18925 |
223 |
40710 |
123 |
47108 |
86 |
51176 |
54 |
53914 |
1871 |
20796 |
220 |
40930 |
121 |
47229 |
85 |
51261 |
54 |
53968 |
1595 |
22391 |
215 |
41145 |
121 |
47350 |
85 |
51346 |
50 |
54018 |
1327 |
23718 |
213 |
41357 |
118 |
47468 |
84 |
51430 |
50 |
54068 |
1184 |
24902 |
212 |
41570 |
118 |
47586 |
84 |
51514 |
48 |
54116 |
1085 |
25987 |
202 |
41772 |
118 |
47704 |
83 |
51597 |
48 |
54164 |
934 |
26921 |
202 |
41972 |
117 |
47821 |
81 |
51678 |
47 |
54211 |
843 |
27764 |
200 |
42172 |
115 |
47936 |
79 |
51757 |
44 |
54255 |
746 |
28510 |
189 |
42363 |
114 |
48050 |
78 |
51835 |
43 |
54298 |
722 |
29232 |
190 |
42553 |
112 |
48162 |
78 |
51913 |
42 |
54340 |
710 |
29943 |
188 |
42741 |
112 |
48274 |
77 |
51990 |
42 |
54382 |
647 |
30589 |
185 |
42926 |
108 |
48382 |
77 |
52067 |
41 |
54423 |
631 |
31221 |
179 |
43105 |
108 |
48490 |
77 |
52144 |
40 |
54463 |
607 |
31828 |
173 |
43278 |
107 |
48597 |
74 |
52218 |
40 |
54503 |
539 |
32367 |
170 |
43448 |
106 |
48703 |
72 |
52290 |
39 |
54542 |
502 |
32868 |
161 |
43609 |
105 |
48808 |
72 |
52362 |
38 |
54580 |
462 |
33330 |
160 |
43769 |
102 |
48910 |
72 |
52434 |
37 |
54617 |
459 |
33790 |
158 |
43927 |
102 |
49012 |
71 |
52505 |
37 |
54654 |
422 |
34212 |
153 |
44080 |
102 |
49114 |
71 |
52576 |
36 |
54690 |
372 |
34584 |
153 |
44233 |
101 |
49215 |
71 |
52647 |
36 |
54726 |
362 |
34945 |
149 |
44382 |
100 |
49315 |
69 |
52716 |
34 |
54760 |
355 |
35300 |
149 |
44531 |
100 |
49415 |
68 |
52784 |
33 |
54793 |
347 |
35647 |
148 |
44679 |
99 |
49514 |
67 |
52851 |
32 |
54825 |
342 |
35989 |
147 |
44826 |
98 |
49612 |
67 |
52918 |
31 |
54856 |
338 |
36327 |
147 |
44973 |
98 |
49710 |
65 |
52983 |
28 |
54884 |
329 |
36656 |
146 |
45119 |
97 |
49807 |
64 |
53047 |
25 |
54909 |
314 |
36970 |
146 |
45265 |
97 |
49904 |
63 |
53110 |
22 |
54931 |
313 |
37283 |
146 |
45411 |
96 |
50000 |
63 |
53173 |
20 |
54951 |
310 |
37593 |
142 |
45553 |
95 |
50095 |
63 |
53236 |
20 |
54971 |
310 |
37903 |
140 |
45693 |
95 |
50190 |
60 |
53296 |
20 |
54991 |
300 |
38203 |
137 |
45830 |
94 |
50284 |
60 |
53356 |
19 |
55010 |
284 |
38755 |
136 |
45966 |
92 |
50376 |
58 |
53414 |
15 |
55025 |
268 |
38755 |
135 |
46101 |
92 |
50468 |
57 |
53471 |
13 |
55038 |
267 |
39022 |
131 |
46232 |
91 |
50559 |
57 |
53539 |
11 |
55049 |
265 |
39287 |
128 |
46360 |
91 |
50650 |
57 |
53528 |
11 |
55060 |
251 |
39538 |
127 |
46487 |
90 |
50740 |
56 |
53641 |
8 |
55068 |
249 |
39787 |
126 |
46613 |
88 |
50828 |
56 |
53697 |
6 |
55074 |
Tableau: 67.1
- Dataset pour analyse de Pareto
où les 200 valeurs
ni (nombre de bons de commande en
provenance d'une ville i) ont
été classées par valeurs décroissantes
et cumulées dans une colonne Ni.
La première ville se caractérise par 8'965 bons
de commande (ce qui correspond à 16.28% du total des bons),
la seconde par 4'555, ce qui fait que les deux premières
villes ont passé 13'520 bons de commande (ce qui correspond
à 24.55% des bons), les trois premières villes, ont
passé 16'589 bons de commande (ce qui correspond à
30.12%), etc. Une autre façon de décrire ce phénomène
consiste à dire: 0.5% des villes (classées par
valeur décroissante du critère) ont passé 16.28%
des bons, 1% des villes ont passé 24.55% des bons, etc.
Ces calculs, sont partiellement
présentés dans le tableau ci-dessous:
i% |
Ni% |
i% |
Ni% |
i% |
Ni% |
i% |
Ni% |
i% |
Ni% |
0.5 |
16.28 |
20.5 |
72.68 |
40.5 |
84.86 |
60.6 |
92.45 |
80.5 |
97.6 |
1 |
24.55 |
21 |
73.11 |
41 |
85.09 |
61 |
92.61 |
81 |
97.7 |
1.5 |
30.12 |
21.5 |
73.51 |
41.5 |
85.32 |
61.5 |
92.77 |
81.5 |
97.8 |
2 |
34.36 |
22 |
73.92 |
42 |
85.54 |
62 |
92.92 |
82 |
97.89 |
... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
19 |
71.33 |
39 |
84.18 |
59 |
91.97 |
79 |
97.3 |
99 |
99.7 |
19.5 |
71.79 |
39.5 |
84.41 |
59.5 |
92.13 |
79.5 |
97.4 |
99.5 |
99. 99 |
20 |
72.24 |
40 |
84.64 |
60 |
92.29 |
80 |
97.5 |
100 |
100 |
Tableau: 67.2
- Données cumulées et normalisées pour analyse de Pareto
traduits graphiquement (selon les traditions d'usage) ci-dessous
sous la forme d'un diagramme de Pareto:

Figure: 67.2 - Diagramme de Pareto
ou de manière plus pertinente sous la forme
d'un diagramme de Lorenz, appelé plus souvent en anglais sous le
nom de "gain chart" (l'abscisse des numéros
des villes est remplacée
par le %cumulé de villes comme dans le tableau de données
ci-dessus):

Figure: 67.3 - Diagramme de Lorenz
Cette analyse met en évidence qu'un nombre faible d'éléments
est à l'origine de la majeure partie du phénomène étudié (par
exemple, ici 31% des villes génèrent 80% des bons
de commande). Ceci explique qu'elle soit l'une des grandes techniques
utilisées dans le domaine de la "gestion
de la qualité totale" (Total Quality Management)
ET dans l'analyse de l'importance des causes d'un problème
de qualité. Elle est également utilisée par
les gestionnaires pour structurer l'organisation, en particulier
pour différencier les processus en fonction de caractéristique
de la demande (suivi différencié de la clientèle
selon son importance, par exemple) et lorsqu'elle est utilisée
pour définir 3 classes, cette technique prend souvent le
nom de "Méthode ABC" (cf.
chapitre de Génie Industriel).
La ligne en pointillés
de ce graphique correspond, elle a ce que nous aurions observé
en cas d'équirépartition du phénomène
étudié, c'est-à-dire si chaque ville s'était
caractérisée par le même nombre de bons de
commande.
De façon générale, plus une courbe de Pareto
(ou de Lorenz) se rapproche de la droite d'égalité parfaite
et plus la répartition de la masse considérée
au sein de la population est égalitaire. En effet, dans
ce cas, la masse (des salaires, de la richesse, du revenu, etc.)
est peu concentrée sur quelques-uns.
Remarque: La présentation de cette analyse a été
faite en classant les observations par valeurs décroissantes,
mais nous aurions pu tout aussi bien partir d'un classement par
valeurs croissantes et, dans ce dernier cas, la courbe obtenue
aurait
été symétrique, le centre de symétrie étant
le point de coordonnées (0.5,0.5).
Dans un environnement industriel,
les points d'amélioration potentiels sont quasi innombrables.
On pourrait même améliorer indéfiniment,
tout et n'importe quoi. Il ne faut cependant pas perdre de
vue que l'amélioration
coûte aussi et qu'en contrepartie elle devrait apporter de
la valeur ajoutée, ou au moins apurer des pertes.
INDICE DE GINI
Le phénomène étudié est d'autant moins équitablement
réparti que la courbe s'éloigne de la droite d'équirépartition.
Les économistes, gestionnaires ou responsables de départements
d'entreprise utilisent parfois (pour leur tableau de bord de performance)
un indicateur synthétique
pour mesurer ce phénomène et son évolution, "l'indice
de Gini" (appelé aussi "coefficient
de Gini").
Ce coefficient est défini par le rapport:
 (67.8)
(67.8)
où les surfaces A et B se rapportent à la
figure ci-après:

Figure: 67.4 - Les deux situations les plus courantes de l'indice de Gini
Le coefficient de Gini est donc un nombre réel compris entre
zéro et 1. En cas d'égalité parfaite, il est égal à zéro (car A=0).
En cas d'inégalité totale il est égal à 1, car B=0. Par
conséquent, à mesure que G augmente de 0 à 1, l'inégalité de
la répartition augmente.
Sachant que la courbe de Lorenz est  on
voit que la surface A+B est égale à la moitié de
cette surface. Nous avons donc: on
voit que la surface A+B est égale à la moitié de
cette surface. Nous avons donc:
 (67.9)
(67.9)
Nous pouvons de ce fait écrire:
 (67.10)
(67.10)
De plus comme:
 (67.11)
(67.11)
Finalement, nous pouvons écrire que:
 (67.12)
(67.12)
En utilisant la méthode de calcul d'intégrale des trapèzes (cf.
chapitre de Méthodes Numériques) nous avons l'aire B qui
est donnée par:
 (67.13)
(67.13)
où pour rappel h est la longueur des intervalles supposés
tous égaux (ce qui est toujours le cas dans le contexte
des analyses de Lorenz) et si la configuration du tableau de données
est telle que nous ayons le graphique suivant (ce qui est plutôt
rare...):

Figure: 67.5 - Choix pour le calcul de l'indice de Gini
Traditionnellement nous trouvons cette dernière relation sous
la forme:
 (67.14)
(67.14)
où n représente le nombre d'unités statistiques
(la population).
Dans la situation où le graphique est sous la forme (cas qui
est nettement le plus fréquent en entreprise et correspond
par hasard à notre exemple!!):

Figure: 67.6 - Deuxième cas pour le calcul de l'indice de Gini
La méthode des trapèzes nous amène alors à écrire:
 (67.15)
(67.15)
Traditionnellement nous trouvons cette dernière relation sous
la forme:
 (67.16)
(67.16)
Dans le cas qui nous sert d'exemple depuis le début avec
le tableau:
i% |
Ni% |
i% |
Ni% |
i% |
Ni% |
i% |
Ni% |
i% |
Ni% |
0.5 |
16.28 |
20.5 |
72.68 |
40.5 |
84.86 |
60.6 |
92.45 |
80.5 |
97.6 |
1 |
24.55 |
21 |
73.11 |
41 |
85.09 |
61 |
92.61 |
81 |
97.7 |
1.5 |
30.12 |
21.5 |
73.51 |
41.5 |
85.32 |
61.5 |
92.77 |
81.5 |
97.8 |
2 |
34.36 |
22 |
73.92 |
42 |
85.54 |
62 |
92.92 |
82 |
97.89 |
... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
19 |
71.33 |
39 |
84.18 |
59 |
91.97 |
79 |
97.3 |
99 |
99.7 |
19.5 |
71.79 |
39.5 |
84.41 |
59.5 |
92.13 |
79.5 |
97.4 |
99.5 |
99. 99 |
20 |
72.24 |
40 |
84.64 |
60 |
92.29 |
80 |
97.5 |
100 |
100 |
Tableau: 67.3 - Données cumulées et normalisées pour analyse de
Pareto
et en adoptant les notations en conséquence, cela donne:
 (67.17)
(67.17)
PERT
PROBABILISTE
En restant toujours dans
le cadre des statistiques et probabilités relativement
aux techniques mathématiques de gestion, il existe une
loi empirique en gestion de projet (domaine que nous supposerons
connu par le lecteur car trivial) très utilisée
dans le cadre des
"PERT probabilistes" (Program Evaluation
and Review Technic) et incluse dans nombres de logiciels spécialisés
afin de faire des prédictions de coûts et de temps
(cf. chapitre de Théorie Des Graphes).
Nous parlons alors de "Probabilistic
Network Evaluation Technic"
(P.N.E.T.).
Cette loi, appelée
"loi bêta" ou encore "loi
de Pert" est souvent présentée
sous la forme suivante dans les ouvrages et sans démonstration
(...):
 (67.18)
(67.18)
et donne la durée probable (espérée)  d'une tâche élémentaire (non décomposable
en sous-tâches)
où nous
avons
d'une tâche élémentaire (non décomposable
en sous-tâches)
où nous
avons  qui sont respectivement les durées optimiste, vraisemblable
et pessimiste de la tâche
qui sont respectivement les durées optimiste, vraisemblable
et pessimiste de la tâche  .
Nous allons démontrer plus bas la provenance de cette relation
et en quoi elle est partiellement fausse! .
Nous allons démontrer plus bas la provenance de cette relation
et en quoi elle est partiellement fausse!
Remarque: Cette approche classique
date de 1962 et est due à
C.E. Clark. Elle serait basée sur une analyse de bases de
données
de tâches de projets. Il faut par contre vérifier
systématiquement
quel type de loi suivent les tâches dans votre entreprise
et ne pas appliquer bêtement et simplement la loi bêta.
Ses principes sont
les suivants: La durée de chaque
tâche du projet est considérée comme aléatoire
et la distribution Bêta est systématiquement utilisée;
les paramètres de cette loi que nous allons démontrer
sont déterminés moyennant une hypothèse de
calcul assez forte, à partir des valeurs extrêmes a
et b que la durée d'exécution peut prendre,
et du mode  . .
Il suffit donc de poser les trois questions suivantes:
1. Quelle
est la durée minimale physiquement possible?
2. Quelle est la durée
maximale au pire?
pour obtenir
respectivement les paramètres  ,
qui permettent ensuite de calculer la moyenne (espérance)
et la variance de
cette durée aléatoire. ,
qui permettent ensuite de calculer la moyenne (espérance)
et la variance de
cette durée aléatoire.
Ensuite, nous déterminons
le chemin critique du projet (par la méthode des potentiels
métra supposée connue par le lecteur), en se plaçant
en univers certain et en utilisant les durées moyennes
(espérées) obtenues avec la loi Bêta, ce
qui permet de trouver le(s) chemin(s) critique(.
Ceci fait, nous nous plaçons alors
en univers aléatoire et la durée du projet est considérée
comme la somme des durées des tâches du chemin critique
précédemment identifié. Nous utilisons alors
le théorème de la limite centrale vu dans le chapitre
de Statistiques (rappelons que ce théorème établit,
sous des conditions généralement
respectées, que la variable aléatoire constituée
par une somme de n variables aléatoires indépendantes
et identiquement distribuées suit approximativement une loi Normale,
quelles que soient les lois
d'origine, dès que n est assez grand) pour approximer
la loi de distribution de probabilités de la durée
d'exécution du projet.
L'espérance mathématique
(ainsi que la variance) de cette loi Normale se calcule comme la
somme des espérances mathématiques (ou des variances)
de chaque durée des tâches du chemin critique (cf.
chapitre de Statistiques) tel que:
 (67.19)
(67.19)
et dans le cas particulier
où les variables sont linéairement indépendantes,
la covariance étant nulle (cf. chapitre
de Statistiques)
nous avons aussi:
 (67.20)
(67.20)
Rappelons que nous avons
vu dans les chapitres de Statistiques et Calcul Différentiel
Et Intégral que:
 (67.21)
(67.21)
et
 (67.22) (67.22)
En gestion nous remarquons que souvent, les durées des tâches
suivent une loi que nous appelons "loi
bêta
de première
espèce" (cf. chapitre de Statistiques)
donnée par:
 (67.23)
(67.23)
Pour un intervalle [a,b] quelconque dans lequel x
est compris, nous obtenons la forme plus générale:
 (67.24)
(67.24)
Vérifions que nous
ayons bien:
 (67.25)
(67.25)
Par le changement de variable:
 et
et  (67.26)
(67.26)
nous obtenons:
 (67.27)
(67.27)
Déterminons maintenant
l'espérance:
 (67.28)
(67.28)
Toujours avec le même
changement de variable, nous obtenons:
 (67.29)
(67.29)
Or:
 (67.30)
(67.30)
Donc:
 (67.31) (67.31)
Calculons maintenant la variance
en utilisant la formule d'Huyghens démontrée dans
le chapitre de Statistiques:
 (67.32)
(67.32)
Calculons d'abord  . .
 (67.33)
(67.33)
Toujours par le même
changement de variable, nous obtenons:
 (67.34)
(67.34)
Or:
 (67.35)
(67.35)
Donc:
 (67.36) (67.36)
Pour finir:
 (67.37)
(67.37)
Calculons maintenant la valeur modale  de cette loi de distribution (pour rappel du chapitre de Statistiques
il s'agit par définition du maximum global de la fonction
de distribution):
de cette loi de distribution (pour rappel du chapitre de Statistiques
il s'agit par définition du maximum global de la fonction
de distribution):
 (67.38)
(67.38)
Il suffit pour le calculer
de résoudre l'équation:
 (67.39)
(67.39)
Après dérivation,
nous obtenons:
 (67.40)
(67.40)
en divisant par  nous avons:
nous avons:
 (67.41)
(67.41)
c'est-à-dire:
 (67.42)
(67.42)
Maintenant, le lecteur aura
remarqué que la valeur a est la valeur la plus petite
et la b la plus grande. Entre deux il y a donc le mode  . .
En gestion de projets, cela correspond respectivement aux durées
optimiste  ,
pessimiste ,
pessimiste  d'une
tâche. d'une
tâche.
Ensuite, nous imposons une
hypothèse assez forte:
 ou
ou  (67.43)
(67.43)
Ce qui implique que nous
ayons:
 (67.44)
(67.44)
ainsi que:
 (67.45)
(67.45)
Et finalement:
 (67.46)
(67.46)
Ce qui nous donne sous forme synthétique:
 (67.47)
(67.47)
Remarque: Les deux dernières expressions de
la variance et de l'espérance sont celles que vous pouvez
trouver dans n'importe quel livre de gestion de projets
(sans démonstration
bien sûr...) comme par exemple le fameux PMBOK. Malheureusement,
il y a deux erreurs dans cet ouvrage de référence
de gestion de projets à ma connaissance (la première
erreur a été corrigée plus tard). Effectivement,
la première erreur c'est que la valeur modale y est
imposée
par le chef de projet alors qu'en toute rigueur elle doit être
calculée
avec la première des trois relations ci-dessus à partir
de la durée pessimiste et de la durée optimiste
de la tâche!!! La deuxième erreur c'est que le
PMBOK dit que la valeur modale est toujours plus petite que
l'espérance.
Ce qui est évidemment faux! Effectivement en posant a =
0 :
 (67.48)
(67.48)
et en simplifiant par b nosu voyons immédiatement que:
 (67.49)
(67.49)
Indiquons qu'exactement les mêmes développements effectués
jusqu'ici sont valables avec la formulation suivante de
la loi bêta à 4 paramètres (qui nous sera aussi très utile
dans le chapitre de Génie Industriel pour des calculs de fiabilité):
 (67.50)
(67.50)
cette dernière formulation étant celle disponible
dans les logiciels ou tableurs comme la version française
de Microsoft Excel 11.8346 par exemple en
utilisant la fonction LOI.BETA( ) et pour sa
réciproque par LOI.BETA.INVERSE( ).
Nous obtenons alors pour l'espérance:
 (67.51)
(67.51)
et pour la variance:
 (67.52)
(67.52)
et le mode:
 (67.53)
(67.53)
Avec:
 (67.54)
(67.54)
Soit dans la version française de Microsoft Excel:
- BETADIST(quantile, ,valeur
optimiste, valeur pessimiste) ,valeur
optimiste, valeur pessimiste)
- BETAINV(probabilité, ,valeur
optimiste, valeur pessimiste) ,valeur
optimiste, valeur pessimiste)
Sinon pour le reste, les résultats (expressions) restent exactement
les mêmes!
 Exemple: Exemple:
Tracé de la fonction de distribution et répartition
pour la fonction de bêta de paramètres  : :
 
Figure: 67.7 - Fonction de distribution et de répartition de la loi bêta
Nous définissons aussi
le "risque d'action" par le rapport
(dont l'interprétation
est laissée aux responsables de projet et aux clients...):
 (67.55)
(67.55)
PROCESSUS SIX SIGMA (LEAN)
Comme nous l'avons vu dans le chapitre de Statistiques, la loi
Normale est une fonction en forme de "cloche" donnée
par:
 (67.56)
(67.56)
dont les écarts-types sont utilisés pour donner
l'intervalle de probabilité
cumulée de se situer dans ces bornes centrées sur
la moyenne comme représenté ci-dessous:

Figure: 67.8 - Rappel des intervalles sigma de la loi Normale
Ceci étant rappelé, nous avons également
présenté dans le chapitre de Génie Industriel
les probabilités conjointes dans le cadre de Six Sigma
pour une chaîne de processus P connectés
en série.
Au fait les processus mentionnés ne sont
pas forcément
des processus industriels mais peuvent être assimilés
sous des hypothèses
identiques à des processus quelconques (administratifs,
procédures,
workflows, etc.).
Nous avions vu que la probabilité conjointe
(ou cumulée)
est appelée dans Six Sigma "Rolled
Troughput Yield" (R.T.Y.) ou "Rendement
Global Combiné" (R.G.C.) et est donnée
par (cf. chapitre de Probabilités):
 (67.57)
(67.57)
Par exemple, l'application de la relation précédente
donne pour un processus série en 4 étapes dont
la fiabilité est
de 90% chaque (sur des structures plus complexes, rappelons
que nous parlons parfois
"d'arbres de probabilités pondérés"):

Figure: 67.9 - Processus série
Nous nous retrouvons donc au final avec une fiabilité
de 65.6% soit une probabilité cumulée de défaut
pour l'ensemble du processus de 34.4 (vous pouvez imaginer aussi
qu'il s'agit de 4 tâches en séquence d'un projet!).
Remarque: Le lecteur attentif aura
remarqué que le système série est toujours
moins fiable que sa composante la moins fiable!!
Redonnons
le tableau au pire selon Six Sigma, soit le tableau en procédé non centré avec
une déviation de la moyenne de 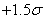 (donc à droite
mais on pourrait prendre à gauche et les résultats sont
les mêmes) par rapport à la cible et d'écart-type unitaire
avec USL et LSL symétriques (ce qui restreint toujours
le champ d'application): (donc à droite
mais on pourrait prendre à gauche et les résultats sont
les mêmes) par rapport à la cible et d'écart-type unitaire
avec USL et LSL symétriques (ce qui restreint toujours
le champ d'application):
Cp |
Cpk |
Défauts (PPM) |
Niveau de qualité Sigma |
Critère |
0.5 |
0 |
501350 |
1.5 |
Mauvais |
0.6 |
0.1 |
382572 |
1.8 |
|
0.7 |
0.2 |
274412 |
2.1 |
|
0.8 |
0.3 |
184108 |
2.4 |
|
0.9 |
0.4 |
115083 |
2.7 |
|
1 |
0.5 |
66810 |
3 |
|
1.1 |
0.6 |
35931 |
3.3 |
|
1.2 |
0.7 |
17865 |
3.6 |
|
1.3 |
0.8 |
8198 |
3.9 |
Limite |
1.4 |
0.9 |
3467 |
4.2 |
|
1.5 |
1 |
1350 |
4.5 |
|
1.6 |
1.1 |
483 |
4.8 |
|
1.7 |
1.2 |
159 |
5.1 |
|
1.8 |
1.3 |
48 |
5.4 |
|
1.9 |
1.4 |
13 |
5.7 |
|
2 |
1.5 |
3.4 |
6 |
Excellent |
Tableau: 67.4
- Défauts et niveau de qualité Sigma en procédé décentré
où nous avons démontré dans le chapitre de Génie
Industriel que les valeurs PPM étaient données par:
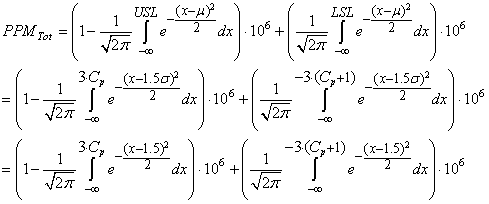 (67.58)
(67.58)
Ce qui donne pour un niveau de qualité de
3 sigmas:
>evalf((1-1/sqrt(2*Pi)*int(exp(-(x-1.5)^2/2),x=-infinity..(1*3))))*1E6+evalf((1/sqrt(2*Pi)*int(exp(-(x-1.5)^2/2),x=-infinity..-(3*(1+1)))))*1E6;
soit une valeur de ~66'810 c'est-à-dire
la valeur de la 6ème ligne. Ce qui correspond à ~6.68%
en termes de probabilité cumulée de non-qualité (66'810
divisé par 1 million et mis en pourcents) et donc respectivement à une
probabilité cumulée
de ~93.32% de qualité.
Nous avons le tableau suivant qui peut résumer
certaines valeurs importantes du tableau précédent
en utilisant la commande Maple 4.00b donnée précédemment:
|

|
|

|

|
Qualité% |
93.32 |
99.38 |
99.98 |
99.9996 |

|
1 |
1.33 |
1.68 |
2 |
Jugement |
Mauvais |
Limite |
Bon |
Excellent |
Tableau: 67.5
- Valeurs importantes de maîtrise du procédé
Sous l'hypothèse que chaque étape d'un processus
série suit
la même loi avec les mêmes moments et les mêmes déviations
par rapport à la cible
nous avons alors pour le RTY:
Étapes/Qualité% |

|
|

|

|
1 |
93.32 |
99.38 |
99.98 |
99.9996 |
7 |
61.63 |
95.73 |
99.84 |
99.9976
|
10 |
50.08 |
93.96 |
99.77 |
99.9966 |
20 |
25.08 |
88.29 |
99.54 |
99.9932 |
40 |
6.29 |
77.94 |
99.07 |
99.9864 |
60 |
1.58 |
68.81 |
98.61 |
99.9796 |
80 |
0.40 |
60.75 |
98.16 |
99.9728 |
100 |
0.10 |
53.64 |
97.70 |
99.966 |
... |
... |
... |
... |
... |
Tableau: 67.6
- Niveau de qualité d'un processus/procédé ayant un nombre fini d'étapes
où chaque ligne représente le Rolled
Troughput Yield (RTY) donc calculé avec:
 (67.59)
(67.59)
où i est le nombre d'étapes
du processus (1, 7, 10, 20, 40) et où les probabilités
sont données
par la première ligne (1). Ainsi, avec un niveau de qualité
de  et
une déviation à la cible de et
une déviation à la cible de  nous
avons pour un processus de 20 étapes identiquement distribuées: nous
avons pour un processus de 20 étapes identiquement distribuées:
 (67.60)
(67.60)
ce qui est lamentable! Un procédé industriel en
20 étapes d'un
produit complet devrait avoir au minimum un niveau de qualité
de 4 sigmas
pour
être acceptable en termes de rendement et de qualité
Ainsi, l'objectif du Lean Six Sigma dans une entreprise sera
d'augmenter le niveau de qualité avec un RTY maximum
pour un nombre donné d'étapes d'un processus.
Remarque: Pour le cas parallèle ou le mélange série/parallèle,
le lecteur est invité à se rendre dans le chapitre de Génie Industriel.
MODÈLE STATISTIQUE DE CONTRÔLE DES SALAIRES
Basé sur les us et coutumes en statistiques, le contrôle statistique
des salaires (C.S.S.) peut se justifier
puisque l'outil et le principe de base est appliqué dans tous
les domaines de l'économie (finance, médecine, ingénierie, qualité,
biologie, projets, logistique, commerce, etc.)
L'idée empirique, fort simple, est d'analyser la distribution
statistique des salaires dans une population (nation, entreprise,
département,
niveau hiérarchique ou autre...) et de considérer tout ce qui
est au-delà de 99.9996% de probabilité cumulée comme une anomalie.
Au contraire, ce qui est à l'intérieur de l'intervalle sera justifié conformément
aux standards d'usage et ne nécessitera dont ni débat, ni explications
hasardeuses.
Déjà, une première règle empirique évidente, est que la variable
aléatoire des salaires doit être catégorisée si sa distribution
statistique est multimodale. Ce qui est fréquent dans certaines
entreprises ou institutions. Il convient ensuite de choisir adéquatement
les catégories qui seront fréquemment des niveaux hiérarchiques
normalisés au sein de l'institution (ressources, responsables
d'équipes, responsables de projets, directeurs de projets, direction...).
Une fois ceci fait, il doit rester une distribution statistique
unimodale dont la variable aléatoire est strictement positive
(les salaires négatifs étant rares...).
Par exemple, pour l'ensemble des salaires bruts annuels fixes
en fin de carrière dans le canton de Genève (Suisse)
en 2004 (source: Office Cantonal Genevois du personnel), nous
avons la
variable aléatoire qui suit une loi log-logistique de
paramètres:
 (67.61)
(67.61)
Nous avons ainsi:
Probabilité cumulée
(ou centile) |
Valeur |
99% |
300'000 |
99.9% |
535'000 |
99.99% |
930'000 |
99.999% |
1'600'000 |
99.9996% |
2'030'000 |
99.9999% |
2'850'000 |
99.99999% |
5'000'000 |
99.999999% |
8'800'000 |
99.9999998% |
13'040'000 |
Tableau: 67.7 - Centile de la répartition des salaires avec valeur correspondante
Ainsi, si nous nous basons sur les us et coutumes en statistiques
de la gestion de portefeuilles et du risque dans les bons instituts
financiers, un salaire annuel de plus de 300'000.- CHF à Genève,
tous secteurs et hiérarchies confondus, est une anomalie...
Si nous nous basons sur les us et coutumes en statistiques
de la gestion du risque et de la qualité dans l'industrie des
procédés de fabrication massive, un salaire annuel de plus de
2'030'000.- CHF à Genève, tous secteurs et hiérarchies confondus,
est une anomalie...
Si nous nous basons sur les us et coutumes des statistiques
les plus pointues en termes de qualité et du contrôle du risque,
un salaire annuel de plus de ~13'040'000.- CHF à Genève, tous
secteurs et hiérarchies confondus, est une anomalie...
Ainsi, il serait contradictoire que les personnes dirigeantes
qui imposent des critères statistiques à leurs collaborateurs
en ce qui concerne les services et la production ne les respectent
pas eux-mêmes en ce qui concerne leur salaire ou n'impose pas
des règles identiques au département des ressources humaines
(dont le concept de qualité statistique est souvent inconnu...).
Remarque: Le même raisonnement statistique peut s'appliquer
pour la part variable du salaire.
GESTION DES STOCKS
L'enjeu de la gestion des
stocks et approvisionnement est important: mettre en place des
processus qui optimisent la fonction économique, sous
contrainte d'une disponibilité en théorie sans
faille. Tels sont les objectifs du gestionnaire de stocks. Cela
suppose
de
disposer
d'une visibilité
sur ses stocks et des méthodologies appropriées aux
différentes situations.
Une production sans stock est quasi
inconcevable vu les nombreuses fonctions que remplissent les stocks.
En effet, la constitution
de stocks est nécessaire
s'il y a: - Non-coïncidence dans le temps ou l'espace de la
production et de la consommation: le stock est
indispensable dans ce cas, car il est impossible
de produire là et quand la demande se manifeste. Les
exemples classiques sont la fabrication de jouets ou la confiserie
pour la non-coïncidence
dans le temps, et les supermarchés pour la non-coïncidence
dans l'espace.
- Incertitude sur le niveau de demande ou sur le prix: s'il
y a incertitude sur la quantité demandée,
on va constituer un stock de sécurité qui permet
de faire face à une pointe de demande (en prenant soin
d'éviter l'effet "coup de fouet").
S'il y a incertitude sur le prix, on va constituer un stock de
spéculation.
Par exemple, les compagnies pétrolières
achètent plus que nécessaire en pétrole
brut lorsque le prix de celui-ci est relativement
bas sur le marché.
- Risque de problèmes en chaîne: il s'agit
ici d'éviter qu'une panne à un poste
ne se répercute sur toute la chaîne d'approvisionnement.
Un retard d'exécution
au poste précédent
ou une grève des transports n'arrêtera pas
immédiatement
l'ensemble du processus de production
s'il y a des stocks tampons.
- Présence de coûts de lancement: dans ce cas,
travailler par lots permet une économie
d'échelle sur les coûts
de lancement de production mais, en revanche,
provoque une augmentation des coûts de possession du stock. Le contrôle du stock
et de l'approvisionnement d'une entreprise est donc aussi fondamental
dans la vie de celle-ci. Afin de réduire (ou optimiser
c'est selon...) un maximum les coûts divers qui tournent
autour du stockage, il faut faire encore une fois appel à des
connaissances en statistiques mathématiques comme nous
allons le voir de suite.
Remarque: L'application de ce type d'outils ne s'adressent
pas vraiment aux P.M.E. de moins de 50 employés produisant
de petites pièces de manière irrégulière
mais plutôt à des
multinationales produisant en énorme quantité
ou en faible quantité des objets de consommation de taille
non négligeable et de manière régulière.
Par ailleurs comme auteur de ces pages, je me suis renseigné dans
de nombreuses entreprises (dont des multinationales!) et je n'ai
trouvé
encore aucun logisticien utilisant dans la pratique les modèles
mathématiques
qui vont être présentés ci-après.
Dans un premier temps, nous
allons établir comment déterminer le stock initial
nécessaire
à une entreprise en se basant sur des données statistiques
et ce à partir de modèles simples ensuite de quoi
nous ferons de même avec les modèles de réapprovisionnement
dont la démarche d'approche est un peu différente
et permet comme pour la première d'arriver à des
résultats
très satisfaisants à grande échelle.
Les modèles que nous
allons construire permettront ainsi:
1. De réguler les
aléas des flux de fournitures
2. De permettre la production
par lots (réduit les coûts de production)
3. De faire face à
des demandes saisonnières
Des stocks supplémentaires
pouvant engranger des "coûts d'intérêt"
(capital immobilisé), des "coûts
d'obsolescence"
(les produits deviennent entre temps obsolètes), des "coûts
de stockage", des "coûts
d'assurances" (protection
contre les accidents pouvant subvenir sur les produits) et de
nombreux
autres...
Nous distinguons dans le domaine classiquement trois types de
stocks:
1. Le "stock minimum",
appelé encore "stock
tampon" ou "stock d'alarme" ou
"point de commande" ou "seuil
de réapprovisionnement" est la quantité de
stock à partir de laquelle on lance une nouvelle commande
pour augmenter les réserves.
2. Le "stock de sécurité" qui permet de répondre aux aléas les
plus fréquents liés à la consommation et à la livraison.
3. Le "stock d'alerte",
appelé encore "stock
critique" qui est
le niveau de stock pour lequel on déclenche une commande
au risque de connaître une rupture. Par construction le stock
d'alerte est donc la somme du stock de sécurité et du stock minimum.
On considère souvent trois stratégies de gestion de stocks:
1. La "gestion de stock par point de
commande": l'approvisionnement
du stock est déclenché lorsque l'on
observe que le stock descend en-dessous du point de commande.
2. La "gestion calendaire":
l'approvisionnement du stock est déclenché à
intervalles réguliers T, par exemple, chaque jour
ou chaque semaine.
3. La "gestion calendaire conditionnelle":
l'approvisionnement du stock est déclenché à intervalles
réguliers T,
mais uniquement lorsque l'on observe que le stock
descend en-dessous du point de commande.
Un stock est constitué pour satisfaire une demande future.
En cas de demande aléatoire, il peut y avoir
non coïncidence entre la
demande et le stock. Deux cas sont évidemment possibles:
1. Une demande supérieure au stock: nous parlons alors de
"rupture de stock"
2. Une demande inférieure au stock: nous parlons alors de "stock
résiduel"
Le critère de gestion généralement retenu
en gestion des stocks est celui de la minimisation
des coûts. Nous noterons cette fonction par la lettre C,
suivie, entre parenthèses (ou en indice), de la ou des
variables de commande du système.
STOCK EN AVENIR INCERTAIN
Commençons notre étude par le cas le plus simple
qui suppose que la consommation est statistiquement régulière
dans le temps et sous contrôle statistique.
Il s'ensuit (cf. chapitres de Statistiques
et de Génie Industriel)
que la consommation périodique suit alors une loi Normale.
Prenons un exemple concret puisque la théorie a déjà été étudiée
en long et en large dans le chapitre de Statistiques.
Considérons un article dont la demande quotidienne suit
donc approximativement une loi Normale de paramètres:
 (67.62)
(67.62)
Le stock disponible au moment de la commande est de 500 unités
et le délai de réapprovisionnement de 5 jours. Nous
souhaiterions savoir quelle est la probabilité cumulée
d'être au-dessus ou égal à la rupture de stock
ainsi que la probabilité cumulée d'être au-dessus
de la consommation quotidienne supposée?
Nous avons pour le premier point la consommation moyenne sur 5
jours qui est en utilisant la propriété de stabilité de
la loi Normale:
 (67.63)
(67.63)
Nous avons alors:
 (67.64)
(67.64)
soit en utilisant la version française de Microsoft Excel 11.8346:
=1-LOI.NORMALE(500;450;44.72;1)=13.17%
Et pour la consommation quotidienne, il vient simplement:
=LOI.NORMALE(90;500/5;20;1)=30.85%
Évidemment, dans la pratique la réalité est
beaucoup moins simple et de plus, la loi Normale peut avoir une
faible probabilité de ventes négatives, ce qui
est peu réaliste...
Mais c'est déjà un
premier modèle qui peut être
confronté à la réalité pour voir
sa puissance prédictive.
STOCK
INITIAL OPTIMAL EN GESTION CALENDAIRE ET à ROTATION NULLE
Imaginons de suite un scénario
afin de développer un autre modèle statistique mais
un tout petit peu plus élaboré que le précédent
(inspiré de
l'ouvrage Gestion de la Production de Vincent Giard).
Nous nous limiterons cependant ici à une loi statistique discrète
et nous referons ensuite un exemple similaire avec une loi continue.
Considérons
pour cela que l'entreprise MAC est la spécialiste d'un
certain produit dont le coût
direct de fabrication par unité est de 25.-
et le prix de vente 60.- par unité (prix supposés
constants et donc indépendants de la quantité et
sans escompte).
La
vente quotidienne de ce produit est,
en semaine, de 2.5 en moyenne et le relevé des demandes
pendant trois mois laisse supposer que celle-ci suit une loi discrète
de type de Poisson (cette fois-ci le support est au moins positif
contrairement
à l'exemple d'avant...), c'est-à-dire que nous avons
une distribution de probabilités
du nombre X de ces produits au
cours d'une journée. Nous tronquerons à
 la
réalisation de cette variable aléatoire car
la probabilité de ventes supérieures à 10
sera supposée comme nulle. la
réalisation de cette variable aléatoire car
la probabilité de ventes supérieures à 10
sera supposée comme nulle.
|
x |
P(X) |
Probabilité cumulée |
|
0 |
0.0821 |
0.0821 |
|
1 |
0.2052 |
0.2873 |
|
2 |
0.2565 |
0.5438 |
|
3 |
0.2138 |
0.7576 |
|
4 |
0.1336 |
0.8912 |
|
5 |
0.0668 |
0.958 |
|
6 |
0.0278 |
0.9858 |
|
7 |
0.0099 |
0.9957 |
|
8 |
0.0031 |
0.9988 |
|
9 |
0.0009 |
0.9997 |
|
10 |
0.0003 |
1 |
Tableau: 67.8 - Probabilités cumulées des ventes
Nous avons alors le tableau
ci-dessus qui nous montre que la quantité la plus souvent
vendue
à un agent économique est à peu près
de 2 (valeur modale) et le calcul de l'espérance
nous donne pour ce tableau:

résultat qui peut aussi bien être interprété comme
la moyenne des ventes quotidiennes que comme la moyenne du niveau
de rupture des
stocks.
Nous supposerons que le stock
est à flux tendu. En d'autres termes, d'un jour à
l'autre, aucune unité n'est reportée pour les ventes
du lendemain car il n'est plus censé y en avoir (ce que
nous appelons la "gestion des stocks
par rotation nulle"). La question
dès
lors est de savoir, le tableau ci-dessus étant
donné, combien de produits mettre en fabrication (ou
commander) chaque jour pour maximiser le bénéfice
et minimiser les pertes.
Dès lors, dans l'optique
retenue de minimisation du coût de possession  (appelé souvent "coût unitaire" de
possession) associé aux
invendus est de 25.- par unité,
tandis que le coût
de rupture
(appelé souvent "coût unitaire" de
possession) associé aux
invendus est de 25.- par unité,
tandis que le coût
de rupture  (appelé souvent "coût unitaire
de rupture") est égal
au manque à gagner
consécutif à
la vente ratée, c'est-à-dire le prix de vente 60.-
soustrait des 25.- soit, un coût de rupture de 35.- par unité.
(appelé souvent "coût unitaire
de rupture") est égal
au manque à gagner
consécutif à
la vente ratée, c'est-à-dire le prix de vente 60.-
soustrait des 25.- soit, un coût de rupture de 35.- par unité.
Remarque: Le coût de rupture
n'est pas assimilé qu'à la perte
engendrée par une vente ratée dans la pratique mais
aussi au
coût d'une
solution de remplacement temporaire proposée par le vendeur
à son client en attente de fournir le bon produit. En interne
dans les entreprises, le coût de rupture entraîne souvent
un chômage
technique des postes en aval lorsqu'une pièce de la chaîne
de fabrication n'est plus disponible.
Une gestion rationnelle doit
permettre de calculer le stock initial S (autrement
dit le nombre de produits à commander ou à
fabriquer pour la journée) qui minimise l'indicateur de
"coût
de gestion" C(S)
défini comme étant la somme du coût de possession
associé au stock moyen des invendus  (appelé
souvent "stock moyen possédé"),
et du coût
de rupture associé au
stock moyen de ventes ratées (appelé
souvent "stock moyen possédé"),
et du coût
de rupture associé au
stock moyen de ventes ratées  (appelé
souvent "stock moyen des invendus"): (appelé
souvent "stock moyen des invendus"):
 (67.65)
(67.65)
Cette relation est cependant un simplification de la relation:
 (67.66)
(67.66)
où le dernier terme est le coût de commande.
Minimiser la fonction de coût C(S) revient
du point de vue mathématique à chercher un extremum
(minimun) de la fonction de coût
de gestion tel que pour la valeur optimale  de
l'approvisionnement initial le coût de
l'approvisionnement initial le coût  soit
immédiatement inférieur à soit
immédiatement inférieur à  c'est-à-dire
inférieur par la droite et par la gauche.
En d'autres termes: c'est-à-dire
inférieur par la droite et par la gauche.
En d'autres termes:
 (67.67)
(67.67)
ou après réarrangement:
 (67.68)
(67.68)
inégalités que le schéma ci-dessous peut aider à mieux comprendre:

Figure: 67.10 - Exemple arbitraire d'extremum de la fonction C(S)
À partir de maintenant la
question est de savoir comment procéder pour déterminer  .
Au fait l'idée est subtile mais simple tant qu'elle est
bien exposée et réfléchie. .
Au fait l'idée est subtile mais simple tant qu'elle est
bien exposée et réfléchie.
Reprenons la distribution
de probabilités de la loi de demande quotidienne et supposons
que nous voulions calculer les ruptures moyennes (donc l'espérance)
pour un niveau donné du stock initial S:
 (67.69)
(67.69)
et:
 (67.70)
(67.70)
associées
aux stocks initiaux respectifs par rapport à la distribution
donnée (bien évidemment x doit être
pris comme étant supérieur à S).
Soit en toute généralité:
 (67.71)
(67.71)
Évidemment, si la loi de probabilité est continue
(ou du moins approximée comme telle), cette dernière
relation s'écrira:
 (67.72)
(67.72)
L'idée est alors
d'écrire la distribution de densité de probabilité
par rapport à la quantité manquante de stock et non
plus vendue:
| x |
P(X) |
x-
4 |
(x-
4)P(X) |
x-
5 |
(x-
5)P(X) |
| 0 |
0.0821 |
- |
- |
- |
- |
| 1 |
0.2052 |
- |
- |
- |
- |
| 2 |
0.2565 |
- |
- |
- |
- |
| 3 |
0.2138 |
- |
- |
- |
- |
| 4 |
0.1336 |
- |
- |
- |
- |
| 5 |
0.0668 |
1 |
0.0668 |
- |
- |
| 6 |
0.0278 |
2 |
0.0556 |
1 |
0.0278 |
| 7 |
0.0099 |
3 |
0.0297 |
2 |
0.0198 |
| 8 |
0.0031 |
4 |
0.0124 |
3 |
0.0093 |
| 9 |
0.0009 |
5 |
0.0045 |
4 |
0.0036 |
| 10 |
0.0003 |
6 |
0.0018 |
5 |
0.0015 |
| 
|
1 |
- |

|
- |

|
Tableau: 67.9
- Distribution de densité de probabilité par rapport à la
quantité manquante
Il ressort du tableau précédent
que le fait de faire passer le stock initial S de
4 à 5, diminue la rupture moyenne en la faisant passer
de 0.1708 à 0.062. Mais de ce résultat, nous ne
pouvons rien faire pour l'instant car à notre niveau actuel
du développement,
cela signifierait qu'en prenant un stock initial de 10, nous aurions
une rupture moyenne nulle (... ce qui n'avance pas à grande
chose...) et que si nous prenons aucun stock initial, nous aurions
une rupture de stock totale...
Mais cependant nous pouvons
tirer un résultat intermédiaire intéressant.
Effectivement regardons la manière dont varie la différence
de la rupture moyenne (résultat facilement généralisable
- nous pouvons faire la démonstration sur demande au
besoin):
 (67.73)
(67.73)
Le résultat étant identique si la loi de probabilité est continue!
Autrement dit (soyez bien
attentif!!!), la diminution de rupture moyenne occasionnée
en augmentant d'une unité un stock préalablement dimensionné à  ,
est égale à la probabilité cumulée que
la demande soit strictement supérieure à celle du
stock initial ,
est égale à la probabilité cumulée que
la demande soit strictement supérieure à celle du
stock initial  . .
En d'autres termes, au cas
où cela ne serait pas clair, le fait d'augmenter le stock
initial diminue certes la rupture moyenne, mais impose en contrepartie
qu'il y ait moins d'acheteurs qui risquent de satisfaire l'offre
et les seuls qui le peuvent sont ceux qui correspondent à
la probabilité cumulée  . .
Finalement, nous pouvons
écrire:
 (67.74)
(67.74)
Le tableau ci-dessous représente
la diminution de rupture moyenne que nous obtenons en accroissant
d'une unité le stock (et respectivement la probabilité
de clients capables de consommer le stock...):
| x |
P(X) |
Ir (x)-Ir (x +
1) |
| 0 |
0.0821 |
0.9179 |
| 1 |
0.2052 |
0.7127 |
| 2 |
0.2565 |
0.4562 |
| 3 |
0.2138 |
0.2424 |
| 4 |
0.1336 |
0.1088 |
| 5 |
0.0668 |
0.0420 |
| 6 |
0.0278 |
0.0142 |
| 7 |
0.0099 |
0.0043 |
| 8 |
0.0031 |
0.0012 |
| 9 |
0.0009 |
0.0003 |
| 10 |
0.0003 |
0 |
Tableau: 67.10
- Rupture moyenne en accroissant
d'une unité le stock
Maintenant regardons les
invendus  en
tant que fonction aléatoire du stock initial S. Leur espérance
est bien évidemment
donnée
par (servez-vous des tableaux au besoin pour comprendre): en
tant que fonction aléatoire du stock initial S. Leur espérance
est bien évidemment
donnée
par (servez-vous des tableaux au besoin pour comprendre):
 (67.75)
(67.75)
Évidemment, si la loi de probabilité est continue
(ou du moins approximée comme telle), cette dernière
relation s'écrira:
 (67.76)
(67.76)
Ce que nous pouvons écrire:
 (67.77)
(67.77)
d'où:
 (67.78)
(67.78)
qui est donc le stock résiduel
de fin de période. C'est donc un résultat remarquable
qui va nous permettre de déterminer  seulement à partir de
seulement à partir de  .
Nous pouvons aussi à nouveau considérer comme intuitif que
le résultat
est identique si la loi de probabilité est continue. .
Nous pouvons aussi à nouveau considérer comme intuitif que
le résultat
est identique si la loi de probabilité est continue.
Cette dernière relation
peut également s'écrire après réarrangement:
 (67.79)
(67.79)
où le terme de gauche
représente la demande moyenne satisfaite et le terme de droite
l'offre moyenne utilisée. Cette relation est donc une relation
particulière d'équilibre entre une offre et une demande.
Nous pouvons par ailleurs
vérifier cela à partir des tables ci-dessous en mettant
un exemple particulier en évidence:

| x |
4 - x |
(4 - x)P(X) |
| 0 |
4 |
0.3284 |
| 1 |
3 |
0.6156 |
| 2 |
2 |
0.5130 |
| 3 |
1 |
0.2138 |
| 4 |
0 |
- |
| 5 |
- |
- |
| 6 |
- |
- |
| 7 |
- |
- |
| 8 |
- |
- |
| 9 |
- |
- |
| 10 |
- |
- |
| |
|
 |
Tableau: 67.11
- Espérance des invendus
Finalement nous pouvons écrire
une expression de  ,
fonction de la seule rupture moyenne: ,
fonction de la seule rupture moyenne:
 (67.80)
(67.80)
ou ce qui s'écrit après réarrangement:
 (67.81)
(67.81)
Il s'ensuit que:
 (67.82)
(67.82)
Ce qui donne avec les résultats
obtenus plus haut:
 (67.83)
(67.83)
Dans ces conditions, les relations:
 (67.84)
(67.84)
Deviennent:
 (67.85)
(67.85)
d'où:
 (67.86)
(67.86)
d'où  est optimal si:
est optimal si:
 (67.87)
(67.87)
Dans notre exemple numérique,
nous avons:
 (67.88)
(67.88)
avec:
 (67.89) (67.89)
d'où le stock optimal initial journalier appelé aussi "stock
minimum" à mettre en production (ou à commander)
pour minimiser le coût de gestion:
 (67.90)
(67.90)
ce qui n'est ni 2 ni 2.5!!! Mais c'est un chiffre
qui est bien évidemment très proche de la valeur modale de la distribution
initiale.
Il faut noter que cependant dans la pratique, les
employés qui font du controlling logistique dans les multinationales
n'ont aucune idée des
prix, marges et coûts qui ont lieu chez leurs clients alors
que ceux-ci leur demande conseil (ils les paient même pour
cela!). Alors souvent on prend simplement la valeur modale ou la
valeur
correspondant
à une couverture de 95% de de la demande périodique
(cela devient assez arbitraire). Dans le cas de notre petite exercice,
la valeur modale du stock initiale arrondi à l'entier supérieur
le plus proche serait 2 et la valeur à 95% de 5. Par prudence
il y a cependant une tendance à prendre plutôt la
valeur modale.
MODÈLES DE WILSON
Il
existe plusieurs modèles d'optimisation de gestion de stocks
(Statistique, Wilson, ABC, 20/80...). Parmi ceux-ci, nous avons
souhaité nous
arrêter sur les "modèles
de Wilson" avec ses trois variantes qui sont
les plus connues (mais pas forcément les plus réalistes...).
Nous considérons donc trois situations:
- L'entreprise se réapprovisionne par
lots à l'extérieur et il
n'y a alors pas d'inertie des stocks et elle relance une commande
lorsque le stock de sécurité est atteint. Nous parlons alors de
"modèle
de Wilson avec réapprovisionnement".
- L'entreprise se réapprovisionne par une production interne
qui implique alors une certaine inertie pour revenir au niveau
de stock désiré. Nous parlons alors
de "modèle de Wilson sans réapprovisionnement" (dont
la totalité des résultats se déduit très
vite du premier modèle sans
refaire tous les développements).
- L'entreprise se réapprovisionne par lots à l'extérieur
et il n'y a alors pas d'inertie des stocks et elle relance une
commande lorsque le stock de sécurité est atteint
mais avec une inertie et demande à ses clients d'attendre.
Nous parlons
alors de "modèle
de Wilson avec attente".
Remarque: Ce modèle appelé également
"modèle du lot économique"
permet de déterminer la fréquence et la quantité
optimale de réapprovisionnement
pour un magasin, une usine... Elle est couramment
employée
par les services logistiques de grandes structures. Elle a en
fait été introduite
dès 1913...
Le
but est de déterminer la stratégie qu'il faut
adopter pour que le total périodique (annuel, mensuel, hebdomadaire,
journalier, ...) des commandes
ou fabrications de pièces minimise le total des coûts
d'acquisition et de possession de stocks pour l'entreprise. Nous
parlons
aussi quelquefois de "gestion à flux
tendu".
L'existence
de stocks au sein de l'entreprise amène le gestionnaire à se poser
la question du niveau optimal de ces derniers, en évitant deux écueils principaux:
1.
Le "surstockage", source
de coûts pour l'entreprise (coût
du stockage physique, manutention, locaux et surfaces utilisées,
coûts
annexes, assurances de gardiennage, coût des capitaux immobilisés).
2.
Le "sous-stockage" qui risque
d'aboutir à des ruptures
de stocks préjudiciables à l'activité de production
ou à l'activité
commerciale de l'entreprise (arrêt de la production, perte de ventes,
perte de clientèle, etc.).
Ainsi, les différents
modèles de gestion des stocks ont pour objectif de minimiser
le coût de gestion dans ce système de contraintes en déterminant
la fréquence de réapprovisionnement et la quantité associée.
Voyons d'abord une approche purement qualitative. Pour chaque
référence, les quantités en stock évoluent
dans le temps par exemple sous une forme:

Figure: 67.11 - Première stratégie de réapprovisionnement
En simplifiant nous obtenons un graphique dit "en dents de scie":

Figure: 67.12 - Diagramme simplifié correspondant en dents de scie
où nous sommes donc dans une situation typique de "gestion
de stocks à rotation non nulle" (c'est-à-dire lorsque
l'invendu
peut être vendu à une période ultérieure.)
Pour éviter la rupture de stock, il faut bien évidemment faire
en sorte que l'entrée d'une commande se fasse, au plus tard, lorsque
la quantité en stock devient nulle:

Figure: 67.13 - Principe visuel de la stratégie
Si nous considérons une consommation
constante d'une quantité N par unité de
temps (jour, mois, année,...) et que nous connaissons à l'avance
le délai d'approvisionnement
(en jour, mois, année...) alors si le tout est mis en
des unités
équivalentes (journalières par exemple) nous avons
le niveau critique qui est donné par:
 (67.91)
(67.91)
qui est aussi assimilé à la terminologie
justifiée
de "point de commande" puisqu'il
s'agit de la quantité que
nous avons en stock à partir de laquelle il faut lancer
une nouvelle commande d'approvisionnement:

Figure: 67.14 - Représentation du point de commande (diagramme
en dents de scie)
Ainsi, si la consommation est de 10 unités
par jour et que le délai d'approvisionnement est de
15 jours, le niveau critique est alors de 150 unités. Pour éviter les aléas (grève, transports, variation
de consommation, remplacements,...) nous envisageons un stock
de sécurité  : :

Figure: 67.15 - Représentation du stock de sécurité sur le diagramme
en dents de scie
Nous avons alors pour le niveau critique:
 (67.92)
(67.92)
Voyons maintenant l'influence du nombre de livraisons sur
le coût de stockage (puisque plus le taux de détention
est gros, plus les coûts de stockage sont élevés).
Supposons pour cela que le marché
consomme 100 unités par mois et ce de manière
régulière.
Dans le cas d'un seul approvisionnement annuel, la consommation
est
représentée
par le graphique ci-dessous (aucun stock de sécurité afin
de simplifier l'exemple):

Figure: 67.16 - Représentation de l'effet d'un seul approvisionnement
où nous voyons immédiatement que le stock moyen
est de 600. Ce stock moyen est obtenu par simple moyenne arithmétique
ou simplement en utilisant la définition de la moyenne
intégrale
de la fonction de consommation:
 (67.93)
(67.93)
Soit trivialement la moitié du stock maximum (ou autrement
vu: la surface du triangle rectangledivisé par T...).
Et si nous divisons la gestion en deux approvisionnements,
nous avons alors:

Figure: 67.17 - Représentation de l'effet de deux approvisionnements
soit un stock moyen deux fois inférieur et dès lors un coût
de stockage moyen deux fois moindre. Mais bien évidemment il
faut y associer le coût d'approvisionnement. C'est à ce niveau
de complexité qu'intervient justement la formalisation mathématique
de Wilson.
Chaque
commande d'achat ou ordre de fabrication coûte donc à l'entreprise.
Le "coût de lancement" ou "coût
de passation" des
commandes ou lancements de fabrications représente tous
les frais liés
(administratifs, réglages machines, préparation,
communications,...) au fait de passer une commande (ou une fabrication)
et est supposé être
proportionnel à la quantité. Ces coûts sont déterminés à l'aide
de la comptabilité analytique.
Ainsi, le
coût d'une commande est obtenu en divisant
le coût
total de fonctionnement du service achat par une grandeur significative
et pertinente. Par exemple, le nombre de commandes passées
(ou ordres de fabrications) annuellement par exemple. Le
coût d'un lancement en fabrication lui sera obtenu en divisant
le coût
total de fonctionnement du service ordonnancement, auquel, il
faut,
ajouter les coûts de réglage des machines et des préséries,
par le nombre de lancements de fabrication.
Ces
valeurs dépendent essentiellement de l'entreprise, de ses
choix en matière de comptabilité analytique. Il est
difficile de définir
une fourchette de valeurs standards. Bon nombre d'entreprises
ne savent
pas à combien leur revient une commande ou un lancement
de fabrication (et bon nombre ne savent tout simplement pas faire
une analyse...).
Le
coût de possession du stock est constitué des charges liées
au stockage physique mais également de la non-rémunération
des capitaux immobilisés
dans le stock (voire du coût des capitaux empruntés pour
financer le stock). Pour cette dernière raison, ce coût
est considéré comme
étant proportionnel à la valeur du stock moyen et à la durée
de détention de ce stock.
Le
taux de possession annuel t% est
le coût de possession ramené à une unité monétaire
de matériel stocké.
Il est obtenu en divisant le coût total des frais annuels de possession
par le stock moyen annuel.
Ces
frais couvrent l'intérêt du capital immobilisé, les
coûts de magasinage (loyer et entretien des locaux, assurances,
frais de personnel et de manutention, gardiennage, etc.), les détériorations
du matériel, les risques d'obsolescence.
Ce
taux oscille habituellement entre 15 et 35% de la valeur marchande
stockée dans les entreprises, suivant le type des articles
et la qualité de
leur gestion des stocks.
Wilson
a établi une relation basée sur un modèle
mathématique
simplificateur dans lequel nous considérons que la demande est
stable sans tenir
compte des évolutions de prix, des risques de rupture
et des variations dans le temps des coûts de commande et de lancement
(nous sommes alors en "avenir certain").
MODÈLE DE WILSON AVEC RÉAPPROVISIONNEMENT
Les
hypothèses très simplificatrices de ce modèle
sont les suivantes:
H1.
La demande périodique est connue et certaine
(déterministe)
H2.
Les quantités commandées sont constantes à chaque période
H3.
La pénurie (ruptures de stock) a lieu en fin de période
(donc il n'y a jamais de défaut de stock)
H4.
Le délai de production est constant et l'approvisionnement
supposé
instantané
H5.
Les coûts (stocks, articles, passation,...) sont invariables dans
le temps
H7. Le coût de possession est proportionnel à la
valeur
H8.
L'horizon de planification est infini
et selon les auteurs cette liste d'hypothèses varie plus
ou moins (certaines hypothèses étant implicites ou
relativement triviales).
Remarques:
R1. Nous supposerons que la gestion du stock
s'effectue sur une période temporelle donnée.
R2. D'après ces hypothèses, nous concluons qu'il
y aura le même niveau de commande à lancer chaque
fois, que le coût total de pénurie est nul.
Nous noterons:
- N la quantité correspondant à une
demande ou respectivement
à des pièces
consommées par période.
- Q la
quantité d'approvisionnements ou de pièces lancées
en fabrication en une seule fois pendant ce même temps (taille
des lots).
-  le
prix unitaire d'achat de la pièce (supposé constant). le
prix unitaire d'achat de la pièce (supposé constant).
-  le
stock de sécurité envisagé pour cette pièce
(supposé constant) pour répondre aux aléas
par période. le
stock de sécurité envisagé pour cette pièce
(supposé constant) pour répondre aux aléas
par période.
- t le
taux de coût de possession en % (supposé constant)
et parfois appelé "taux de détention".
-  le
coût d'approvisionnement/acquisition par commande ou de lancement
de fabrication. le
coût d'approvisionnement/acquisition par commande ou de lancement
de fabrication.
Nous définissons de par la même
occasion, le "coût unitaire de
stockage" calculé souvent (mais pas uniquement!)
sur la base du prix unitaire d'achat d'une pièce:
 (67.94)
(67.94)
Propositions:
P1.
Le rapport:
 (67.95)
(67.95)
donne "l'inertie des stocks" ou
qui peut être vu de manière plus explicite comme étant
le "nombre
périodique de lancements" (ou la cadence de
réapprovisionnement) pour
satisfaire la demande. L'inertie des stocks a donc la dimension
d'un inverse du temps.
P2.
Le "coût d'inertie" ou respectivement
le "coût
d'acquisition", ou encore "coût
de lancement" est
donc par unité de période de:
 (67.96)
(67.96)
Ce
dernier est donc supposé proportionnel à la consommation!
Ce qui est important ceci dit est de remarquer que le coût
de lancement est inversement proportionnel à la quantité Q et
donc qu'il tend vers zéro lorsque Q tend vers l'infini.
Ceci dit, normalement on aura dans la majorité des cas théoriques:
 (67.97)
(67.97)
P3.
Le stock moyen dans l'entreprise dans l'hypothèse d'une
consommation (décroissance linéaire
du stock) et d'un niveau de sécurité constants
dans le temps est trivialement par période:
 (67.98)
(67.98)
Le
"coût périodique de possession",
appelé encore "coût
de possession" ou "coût
de gestion" ou "coût
de stockage" ou "coût
de détention"...,
est alors:
 (67.99)
(67.99)
Il s'agit donc de la fonction d'une droite (dont l'ordonnée à
l'origine est non-nulle si le stock de sécurité est
non nul) si nous considérons
que uniquement Q y est variable. Il est important de remarquer
que ce coût ne prend pas en compte les concepts de remise
de volume faite par les commerciaux...
Ces
propositions nous amènent donc à l'équation du "coût
total d'approvisionnement", appelé aussi "coût
total de stockage" que nous allons chercher à minimiser:
 (67.100)
(67.100)
et qui donne une "courbe (hyperbolique)
des coûts
cumulés" du
type:

Figure: 67.18 - Courbe des coûts cumulés
Trouver
la quantité économique  ,
c'est trouver la valeur de Q pour laquelle le coût total
est minimal (en d'autremes termes c'est chercher la taille du
lot qui permette de rentabiliser au mieux tous les coûts de stockage,
fabrication,, etc.), c'est-à-dire mathématiquement
la valeur ,
c'est trouver la valeur de Q pour laquelle le coût total
est minimal (en d'autremes termes c'est chercher la taille du
lot qui permette de rentabiliser au mieux tous les coûts de stockage,
fabrication,, etc.), c'est-à-dire mathématiquement
la valeur  pour
laquelle la dérivée du coût total par rapport à la
quantité est
nulle: pour
laquelle la dérivée du coût total par rapport à la
quantité est
nulle:
 (67.101)
(67.101)
D'où la "relation de Wilson"
(après un calcul élémentaire), appelée aussi
simplement "formule de Wilson", pour le "lot/quantité économique
optimal":
 (67.102)
(67.102)
qui est donc pour rappel, le taille du lot qui minimise le coût
total (indépendante du stock de sécurité qui
s'annule lors de la dérivée). Nous constatons que la
quantité économique est proportionnelle à la racine carée de la consommation.
Donc grossièrement une article vendu 100 fois plus par une société
nécessitera qu'un stock moyen 10 fois supérieur.
Bien évidemment une fois connue la quantité économique,
il devient facile de calculer le "coût
de gestion optimal par période"  en
injectant en
injectant  dans
la relation obtenue plus haut: dans
la relation obtenue plus haut:
 (67.103)
(67.103)
ainsi que la "cadence ou fréquence
optimale de réapprovisionnement"
puisque donnée par le rapport:
 (67.104)
(67.104)
Nous avons alors après un peu d'arithmétique élémentaire
le coût de gestion optimal par période qui est donné par:
 (67.105)
(67.105)
Comme souvent, les gestionnaires aiment bien faire de l'analyse
de la sensibilité (nous en avons déjà fait
mention lors de notre étude du seuil de rentabilité).
Dans le domaine de la gestion de stock il est de tradition de faire
l'analyse de la sensibilité de la variation relative du
coût total de stockage par rapport au coût de gestion
optimale par période:
 (67.106)
(67.106)
Mais comme le  (coût
du stock de sécurité)
est supposé indépendant de la quantité, il
est d'usage de ne considérer que la variation relative indépendamment
de ce terme telle que: (coût
du stock de sécurité)
est supposé indépendant de la quantité, il
est d'usage de ne considérer que la variation relative indépendamment
de ce terme telle que:
 (67.107)
(67.107)
Enfin, il est d'usage de simplifier la forme analytique de cette
dernière relation sous la forme suivante après quelques
manipulations algébriques élémentaires:
 (67.108)
(67.108)
c'est donc un résultat assez esthétique... que
le lecteur remarquera au passage comme étant toujours positif!
Il est évident que nous tirons aussi de la relation de
la fréquence optimale de réapprovisionnement
la "période optimale de réapprovisionnement"
donnée alors par (l'inverse de la fréquence par définition):
 (67.109)
(67.109)
Si
nous reportons sur un graphique les fonctions:
-
coût de lancement (approvisionnement) en fonction des quantités
-
coût de possession en fonction des quantités
-
coûts totaux en fonction des quantités
alors la
quantité économique se trouve à l'intersection
des deux courbes, lancement et possession (lorsque le coût
de possession est égal au coût d'acquisition),
ou au point d'inflexion de la courbe cumulée.
Dans la pratique toutefois, il est possible de commander exactement
la quantité économique, on choisira une taille de
lot répondant
aux diverses contraintes et comprise dans la "zone économique":

Figure: 67.19 - Représentation de la zone économique
Évidemment dans certaines entreprises un objectif est plutôt
d'essayer de diminuer le coût de stockage afin d'atteindre
l'équivalent de la demande comme quantité économique.
Nous avons alors avec un peu d'algèbre élémentaire:
 (67.110)
(67.110)
soit au final le coût de stockage optimal si la quantité
d'approvisionnement Q est imposée:
 (67.111)
(67.111)
Donc pour résumer, il faut savoir que l'on considère souvent que
l'ensemble du modèle de Wilson se résume aux 5 relations ci-dessous:
 (67.112)
(67.112)
Il
existe un autre type de cas de figure qu'il faut étudier.
Si l'on commande en quantités plus importantes en bénéficiant
ainsi d'une remise, on augmente certes les coûts de possession
mais on réduit
théoriquement le nombre de commandes annuelles.
L'objectif
pour le gestionnaire est bien sûr
de vérifier mathématiquement que la remise consentie
par son fournisseur n'entraîne pas de coûts induits supérieurs à
la remise (ce serait une preuve d'incompétence du gestionnaire!).
Pour
ce faire, il faut ramener tous les coûts à une pièce
telle que le coût total unitaire s'écrive:
 (67.113)
(67.113)
cette
relation est importante, car elle détermine la valeur de
la remise pour que cette dernière soit intéressante.
Pour
connaître le seuil de remise R
pour une quantité donnée, on remplace dans la relation
précédente,
Q
par la quantité visée Q' et
 par par
 ,
R
étant la remise. ,
R
étant la remise.
Nous
résolvons alors l'équation et nous obtenons:
 (67.114)
(67.114)
Nous déterminerons donc la valeur limite de R
sous laquelle la remise ne compense pas les coûts internes.
Dans
la pratique nous ne pouvons commander exactement la quantité optimale
 ,
notamment du fait des unités d'achats imposées par les fournisseurs
(quantités minimales, conditionnements, etc.). Il est donc plus
judicieux de s'intéresser à la "zone économique",
constituée
par la partie inférieure (le ventre) de la courbe des coûts totaux. ,
notamment du fait des unités d'achats imposées par les fournisseurs
(quantités minimales, conditionnements, etc.). Il est donc plus
judicieux de s'intéresser à la "zone économique",
constituée
par la partie inférieure (le ventre) de la courbe des coûts totaux.
Du
fait des hypothèses simplificatrices, le modèle de
Wilson ne peut fournir au mieux qu'un ordre de grandeur si consommation
et/ou prix
sont sujets à variations (puisqu'elle est extrêmement dépendante
des deux paramètres subjectifs: coûts de stockages
et lancements).
Le
recours aux lancements de fabrication économiques est "anti-flexible"
par essence. Ce genre de politique amène fréquemment
des conséquences importantes, risque de gonfler le stock de produits
finis, reportant
les coûts et pertes en aval du processus.
Cependant,
le modèle de Wilson a ceci d'intéressant qu'il peut
s'appliquer
également assez bien à des ressources humaines.
 Exemple: Exemple:
L'entreprise MAC utilise un article
X330 pour lequel la consommation prévisionnelle de l'année
N devrait être de 4'000 articles.
Les données sont les
suivantes:
- Le coût unitaire de l'article
X330 est de  (peu importe le numéraire)
(peu importe le numéraire)
- Le coût de passation/lancement d'une
commande est de 
- Le taux de possession du stock est
de  par
an par
an
- Le stock de sécurité est de 250 unités
Le fournisseur de cet article, pour
inciter ses clients à augmenter l'importance de leurs commandes,
propose à l'entreprise les conditions suivantes:
C1. Quantités commandées
inférieures à 2'000 unités: prix unitaire

C2. Quantités commandées
comprises entre 2'000 et 3'500 unités: remise de 2%.
C3. Quantités commandées
supérieures à 3'500 unités: remise de 3 %.
Travail à faire: Dire quelle
solution l'entreprise doit adopter.
Le prix varie donc en fonction de la
quantité tel qu'étant donnée une quantité
choisie, la remise s'applique d'une façon équivalente
à tous les articles (nous parlons alors de "remise
uniforme").
D'après l'énoncé
et en fonction de Q la quantité d'approvisionnement,
nous savons que:
1. Si 
2. Si 
3. Si 
En fonction de la relation de Wilson
du lot économique, nous allons calculer la quantité économique
 pour le prix le plus avantageux à savoir
pour le prix le plus avantageux à savoir  : :
 (67.115)
(67.115)
Mais pour avoir
droit à  il faut commander au minimum 3'500 articles il y a donc contradiction
et cette solution est donc hors zone. Des calculs identiques (que
nous laissons le soin de faire avec la calculatrice quand même...)
montrent que seul le lot économique
il faut commander au minimum 3'500 articles il y a donc contradiction
et cette solution est donc hors zone. Des calculs identiques (que
nous laissons le soin de faire avec la calculatrice quand même...)
montrent que seul le lot économique  de
de  correspond à la contrainte
correspond à la contrainte  . .
Dès lors, la période
optimale de réapprovisionnement correspondante sera:
 (67.116)
(67.116)
et le coût
de gestion optimal par période:
 (67.117)
(67.117)
Attention! Pour ce dernier calcul, certains auteurs
incluent dans la coût du stock de sécurité  la
quantité N. Il s'agit d'un choix plutôt discutable
et qui nécessiterait d'être précisé. la
quantité N. Il s'agit d'un choix plutôt discutable
et qui nécessiterait d'être précisé.
Enfin, l'impact sur le coût total de gestion
si nous augmentons ou diminuons la quantité de plus ou moins
30% par rapport à la quantité économique est donné par:  (67.118)
(67.118)
Donc évidemment, cela ne fait que d'augmenter
les coûts et comme nous l'avons vu sur le graphique plus
haut, la courbe n'étant pas symétrique, les deux
résultats ne sont pas égaux.
MODÈLE DE WILSON SANS RÉAPPROVISIONNEMENT
Dans le modèle précédent, nous
avons donc supposé
une gestion de stocks en dents de scie de la forme suivante:

Figure: 67.20 - Représentation schématique du modèle de Wilson avec
réapprovisionnement
Dans le modèle qui va nous intéresser
maintenant, nous allons considérer une gestion de stock
avec une inertie du réapprovisionnement souvent due à une production
à l'interne sous la forme suivante:

Figure: 67.21 - Représentation schématique du modèle de Wilson sans
réapprovisionnement
Donc dans la figure ci-dessus, nous pouvons observer
que la demande de production se fait au point de commande et que
pendant la production au rythme de P pièces par
unité
de temps pendant un temps  ,
la consommation N par période T (rapportée à l'unité
de temps de la production), tape déjà dans les stocks
générés. ,
la consommation N par période T (rapportée à l'unité
de temps de la production), tape déjà dans les stocks
générés.
Devons-nous donc refaire tous les calculs du modèle
précédent? La réponse est: non pas en totalité!
Car si nous réfléchissons
un tout petit peu en observant la fonction hyperbolique
du coût
total de stockage que nous avons démontrée plus haut:
 (67.119)
(67.119)
Il est évident que le premier terme dû au
réapprovisionnement n'a aucune raison
de changer. Le troisième terme, dû au stock de sécurité,
n'a aucune raison de changer non plus! Donc il ne reste que le
deuxième terme
représenté par le coût de stockage moyen qui
est forcément différent!
Donc le stockage moyen n'est plus:
 (67.120)
(67.120)
Nous pourrions calculer facilement la surface moyenne
du triangle en utilisant la formule de Héron pour le calcul
de la surface d'un triangle quelconque démontré dans
le chapitre de Formes Géométriques. Mais le problème
dans le cas présent, c'est
que nous voulons faire apparaître Q dans le stock
moyen. Nous ne pourrons alors utiliser la formule de Héron.
L'idée va être la suivante (se référer à la figure précédente):
Lorsque l'entreprise n'a plus de stock, elle en lance
pendant un temps  la
production à un rythme de P éléments
par unité temporelle jusqu'à atteindre en cumul la
quantité objectif Q. Nous avons alors: la
production à un rythme de P éléments
par unité temporelle jusqu'à atteindre en cumul la
quantité objectif Q. Nous avons alors:
 (67.121)
(67.121)
Mais en même temps qu'elle produit (et après aussi),
l'entreprise consomme N éléments par unité temporelle.
Le stock réel généré sera alors au temps  (sous
la condition évident que P est
supérieur à N) l'inventaire maximum: (sous
la condition évident que P est
supérieur à N) l'inventaire maximum:
 (67.122)
(67.122)
Cet inventaire maximum correspond donc à la hauteur
de notre triangle quelconque (toujours se référer à la figure précéente)
mais nous souhaitons y faire apparaître le stocke obejctif Q.
Donc, pour cela, il n'y a maintenant rien de plus simple en utilisant
la relation antéprécédente:
 (67.123)
(67.123)
Donc le stock moyen devient:
 (67.124)
(67.124)
Donc nous voyons que la seule différence entre les
deux modèles est le facteur:
 (67.125)
(67.125)
Dès lors, les relations obtenues dans le modèle
de Wilson avec réapprovisionnement (du moins les plus importantes)
et qui étaient pour rappel:
 (67.126)
(67.126)
deviennent (la dernière relation ne change pas):
 (67.127)
(67.127)
L'adaptation des relations du coût
périodique
de possession et du coût total
d'approvisionnement sont quant à eux immédiats.
Donc à la différence du modèle avec approvisionnement,
nous voyons que seulement une nouvelle variable P apparaît
est qui est donc la vitesse de production (éléments produits
par unité de temps) pour permettre une production de N éléments
par unité de temps. Ce que lecteur ne doit pas oublier lors de
cas d'application numérique, c'est de rapporter P et N
à la même unité de temps.
MODÈLE DE WILSON AVEC RÉAPROVISIONNEMENT
ET RUPTURE
Dans les grands classiques d'études scolaires
(le reste étant ensuite une combinaires cas des différents
scénarios
basé
sur
le même raisonnement), voyons le modèle de Wilson
avec réaprovisionnement
(instantané) mais où la rupture et la vente à découvert
(en contrepartie d'une pénéalité) est autorisé (donc
il n'y a pas de stock de sécurité!).
Nous représenterons ce scénario
par la figure en dents-de-scie suivante:

Figure: 67.22 - Représentation schématique du modèle de Wilson avec
réapprovisionnement et rupture
Nous considéreron  comme
étant la perte financière
(coût) par unité de pièce pendant la période à découvert
(ne pas encaisser l'argent tout de suite fait que nous en perdons
rien que par le fait que nous ne pouvons pas le placer sur des
fonds à rendement comme
étant la perte financière
(coût) par unité de pièce pendant la période à découvert
(ne pas encaisser l'argent tout de suite fait que nous en perdons
rien que par le fait que nous ne pouvons pas le placer sur des
fonds à rendement
Pour ce cas là, nous n'avons pas trouvé de manière
simple d'éviter de refaire les calculs des relations du modèle
de Wilson avec réaprovisionnement (bon si quelqu'un a une astuce
nous sommes preneurs). Cependant il s'agit toujours d'algèbre
élémentaire donc le lecteur ne devrait souffrire d'aucune difficulté
face à ce genre d'exercice de style.
Nous avons d'abord trivialement en se référant
à la figure ci-dessus:
 (67.128)
(67.128)
D'abord, le coût de stockage moyen est trivialement
de:
 (67.129)
(67.129)
Le coût moyen de vente en rupture est lui
aussi donné trivialement par:
 (67.130)
(67.130)
Le coût moyen total sur une période est alors
de:
 (67.131)
(67.131)
Rapportons maintenant cela au temps d'une période:
 (67.132)
(67.132)
Le coût total moyen par période est alors de:
 (67.133)
(67.133)
Le problème ici c'est que Q dépend
de M et inversement. Nous allons donc devoir faire usage
des dérivées partielles pouf fixer tantôt l'un et tantôt l'autre.
Donc pour trouver la quantité économique, nous
allons arbitrairement d'abord déterminer quelle est
la quantité M qui
va minimiser le coût total moyen par période (ceci
afin de se débarasser par anticipation de la présence
de la variable M dans
l'expression de la quantité économique). Nous avons
alors en prenant la dérivée partielle (donc sous-entendu
que nous maintenons toutefois Q constant):
 (67.134)
(67.134)
Soit:
 (67.135)
(67.135)
Maintenant, pour la quantité économique, nous avons
respectivement en prenant la dérivée partielle (dons sous-entendu que nous
fixons M):
 (67.136)
(67.136)
En y injectant le résultat antéprécédent il vient:
 (67.137)
(67.137)
Soit après quelques manipulations algébrique élémentaires:
 (67.138)
(67.138)
Ce qui donne finalement:
 (67.139)
(67.139)
Nous avons alors explicitement:
 (67.140)
(67.140)
La période optimale de réapprovisionnement
est alors:
 (67.141)
(67.141)
La quantité m économique de rupture donnant le
déclenchement de lancement de restockage est alors:
 (67.142)
(67.142)
Un difficulté pratique de ce modèle est de déterminer  .
L'idée est alors de l'estimer sur la durée maximale d'attente supposée du client
ayant fait une commande lors d'une rupture. En partant de: .
L'idée est alors de l'estimer sur la durée maximale d'attente supposée du client
ayant fait une commande lors d'une rupture. En partant de:
 (67.143)
(67.143)
Et en mettant au carré dans l'idée d'extraire  : :
 (67.144)
(67.144)
Nous avons donc finalement une équation du deuxième degré:
 (67.145)
(67.145)
Dont les deux racines réelles sont:
 (67.146)
(67.146)
La racine qu'il faut garder est celle qui donne un coût de rupture
positif. Soit:
 (67.147)
(67.147)
Avant de passer à l'exemple pratique, le résumé se réduit à:
 (67.148)
(67.148)
 Exemple: Exemple:
L'entreprise MAC livre un article X330. Dans le but de ne pas
perdre ses clients, les gestionnaires décident d'un temps de rupture
optimal (sous-entendu: maximuM) de 2 jours. Nous avons les données suivantes:
 (67.149)
(67.149)
Ce qui donne:
 (67.150)
(67.150)
ANALYSE DE LA SENSIBILITÉ
Dans le domaine de la gestion (projets, finance, statistique)
et du cas multivaré, l'analyse de la sensibilité est
une technique simple basée
sur l'utilisation du coefficient de corrélation linéaire
(de Pearson) démontré dans le chapitre de Statistiques
dont une écriture possible
est (dans le cas bivarié):
 (67.151)
(67.151)
et une écriture parfaitement équivalente démontrée dans le chapitre
de Méthodes Numériques:
 (67.152)
(67.152)
avec pour rappel:
 (67.153)
(67.153)
L'idée est que si nous avons une variable principale qui
dépend
de manière sous-jacente de plusieurs variables alors nous
calculons le coefficient de corrélation (ou le coefficient
de détermination
qui est simplement le carré du coefficient de corrélation)
de la variable principale avec chacune des variables sous-jacentes.
Prenons un exemple simple et particulier au monde de la gestion
de projets. Imaginons un projet dont le planning est basé un
chemin critique basé uniquement de deux tâches A et B.
La première tâche A s'étale sur une
durée dont
la loi est Normale de paramètres:
 (67.154)
(67.154)
soit une durée espérée de 8 jours et un écart-type
de 1 jour et la tâche B s'étale sur une durée
suivant une loi bêta
(selon recommandation du PMI...) de paramètres (5,12), soit
une durée optimiste de 5 jours et une durée pessimiste
de 12 jours:
 (67.155)
(67.155)
Faisons pour l'exemple une simulation de Monte-Carlo à 1'000
itérations
avec la version anglaise de Microsoft Excel 11.8346 (puisque
la majorité des
gestionnaires travaillent avec la version anglaise):

Figure: 67.23 - Simulation de deux petites tâches respectivement avec une distribution
Normale et bêta
Ensuite, nous calculons toujours avec la version anglaise de Microsoft
Excel 11.8346 le coefficient de corrélation:

Figure: 67.24 - Calcul du coefficient de corrélation entre les sommes et les tâches
ce qui donne:

Figure: 67.25 - Corrélation correspondante
Soit sous la forme d'un graphique de type "tornado
chart" comme
il est d'usage dans le domaine de l'analyse de la sensibilité:

Figure: 67.26 - Tornado chart obtenu avec Microsoft Excel 11.8346
Il est dangereux d'utiliser le coefficient de corrélation
(de Pearson) lorsque la relation entre la variable principale et
les
variables sous-jacentes n'est pas linéaire! Cependant, les
logiciels peuvent identifier de quel autre type de relation il
s'agit (exponentielle,
logarithmique, puissance, polynomiale) et faire une transformation
pour ramener l'équation à celle d'une droite. Cependant,
cette manipulation peut aussi amener à des erreurs grossières
dans certains cas. La majorité des logiciels spécialisés
utilisent alors la définition
empirique de la régression que nous avons vue dans le chapitre
de Méthodes Numériques:
 (67.156)
(67.156)
et utilisent alors la recherche opérationnelle (cf.
chapitre de Méthodes Numériques) pour déterminer les paramètres de l'équation
qui minimisent le  selon
la relation précédente. selon
la relation précédente.
Un logiciel spécialisé pour obtenir très rapidement ce genre
d'analyse sur des situations complexes est @Risk de Palisade qui
donne lui le graphique suivant:

Figure: 67.27 - Tornado chart de la même simulation obtenu avec @Risk
Enfin, quand nous avons un très grand nombre de variables sous-jacentes,
il peut être intéressant de regrouper les coefficients de corrélation
par intervalles avec un graphique du type suivant (exemple pris
de la bourse) où l'ordonnée représente le % du nombre de variables:

Figure: 67.28 - Analyse des groupes de corrélation de variables
Ainsi, par exemple, ci-dessus 32% des variables ont un coefficient
de corrélation nul avec la variable principale (qui est l'indice
de performance du portefeuille concerné) et 14% ont un coefficient
de corrélation compris entre +0.75 et +1.
Il est aussi courant de représenter l'influence en % de chaque
variable sur la variable principale en faisant la moyenne des rapports
entre les deux. Ce qui donne le graphique suivant si nous en avons
un grand nombre:

Figure: 67.29 - % d'influence sur la variable principale en fonction de la corrélation
Ainsi, par exemple, nous pouvons observer sur le graphique ci-dessus
qu'une variable a une influence moyenne de +4% sur l'indice du
portefeuille avec une corrélation de +0.5.
Bref... libre cours pour faire le graphique que l'on veut en
fonction des besoins de son entreprise!
Enfin, indiquons que certains contrôleurs financiers parlent à
tord "d'analyse de la sensibilité" lorsqu'ils font des analyses
à double entrée à l'aide de tableurs.Voyons de quoi il s'agit avec
le petit exemple simple illustré ci-dessous avec le tableur MS
Excel 14.0.7151.
BIENS
D'ÉQUIPEMENT
Les installations,
les biens d'équipement subissent une dépréciation
progressive due à l'usure ou à l'obsolescence. Cette
baisse de valeur, enregistrée comme une charge en comptabilité,
est appelée "amortissement comptable".
Il ne faut pas confondre l'amortissement financier vu dans
le chapitre d'Économie
qui correspond au remboursement d'une dette et l'amortissement
comptable
qui est une diminution de valeur des moyens de production.
Certains types
de biens ont une perte de valeur assez uniforme dans le temps contrairement
à d'autres qui se déprécient plus rapidement
les premières années. Nous allons présenter
ici quelques-unes des méthodes comptables utilisées
en pratique qui décrivent l'un ou l'autre de ces phénomènes.
AMORTISSEMENT
LINÉAIRE
Définition: Nous parlons d'un "amortissement
linéaire" d'un
bien lorsque sa valeur d'immobilisation est diminuée
(amortissement) d'un montant périodique
(annuel dans la comptabilité) constant durant sa durée
de vie:
Ainsi, si nous
notons  le montant du k-ème amortissement et
le montant du k-ème amortissement et  la valeur initiale du bien d'équipement et
la valeur initiale du bien d'équipement et  sa valeur finale souhaitée (qui dans la plupart des cas
sera nulle), nous avons:
sa valeur finale souhaitée (qui dans la plupart des cas
sera nulle), nous avons:
 (67.157)
(67.157)
Il est possible d'obtenir la valeur d'amortissement en utilisant
la fonction AMORLIN( ) de la version française de Microsoft Excel 11.8346.
Le taux d'amortissement équivalent constant basé sur
la valeur d'achat et résiduelle est alors donné évidemment
par:
 (67.158)
(67.158)
À remarquer que ce taux constant ainsi que la valeur finale
sont parfois imposés par
la législation
dans certains pays (comme c'est le cas en Suisse par exemple) jusqu'à
une valeur résiduelle nulle ou non nulle elle aussi définie
par la législation!
AMORTISSEMENT
ARITHMÉTIQUE DÉGRESSIF
Définition: Lorsque la valeur d'immobilisation
(amortissement) d'un bien décroît
inversement à l'ordre des périodes (années
en comptabilité) nous parlons alors "d'amortissement
arithmétique
dégressif" (donc pas de taux d'amortissement imposé par
l'État possible!).
Par exemple,
un bien d'une durée de vie de 4 ans, sera amortissable de
4/10 la première année, 3/10 la seconde, 2/10 la
troisième
et 1/10 la dernière. La base commune "10" (dans cet exemple)
étant la somme arithmétique 1+2+3+4 afin que la totalité
des fractions soit égale à l'unité. Il s'agit
d'une règle purement fiscale américaine " Sum-of-Years
Digits" (SYD).
Remarque: Il ne faut pas confondre
"l'amortissement arithmétique dégressif" avec "l'amortissement
dégressif" qui consiste à appliquer un coefficient
multiplicateur (édicté par le fisc) au pourcentage
d'amortissement linéaire correspondant et que nous ne traiterons
pas sur ce site (sauf demande explicite d'un lecteur). Il ne
peut être
utilisé que
pour des biens neufs et ne concerne pas tous les types d'immobilisation.
Ce
taux d'amortissement dégressif s'applique chaque année
sur la valeur comptable résiduelle du bien.
Soit  le k-ème
amortissement et le k-ème
amortissement et  la valeur initiale du bien d'équipement et
la valeur initiale du bien d'équipement et  sa valeur finale souhaitée (qui dans la plupart des cas
sera nulle) nous avons alors:
sa valeur finale souhaitée (qui dans la plupart des cas
sera nulle) nous avons alors:
 (67.159)
(67.159)
ce qui peut
s'écrire:
 (67.160)
(67.160)
et comme nous
l'avons démontré dans le chapitre des Suites Et Séries:
 (67.161)
(67.161)
ce qui nous
amène à écrire:
 (67.162)
(67.162)
Il est possible d'obtenir l'amortissement à une période k en
utilisant la fonction SYD( ) de la version française de Microsoft
Excel 11.8346.
AMORTISSEMENT
GÉOMÉTRIQUE DÉGRESSIF
Définition: Lorsque la valeur d'immobilisation
d'un bien décroît
selon un taux d'amortissement constant basé sur la valeur
résiduelle
de la période précédente (donc en quelque
sorte comme un intérêt
composé à taux négatif), nous parlons alors "d'amortissement
géométrique dégressif simple".
Ainsi, la valeur
du bien après n années est définie
par:
 (67.163)
(67.163)
avec donc:
 (67.164)
(67.164)
Remarque: Nous constatons que la valeur
de t% étant
comprise dans l'intervalle entre [0,1[ la limite de 
quand n tend vers l'infini n'est jamais nulle. Ainsi, la
valeur résiduelle ne le sera jamais non plus !
Sachant
par définition de cet amortissement que:
 (67.165)
(67.165)
nous
obtenons:
 (67.166)
(67.166)
En injectant
l'expression du taux dans la relation précédente,
nous obtenons:
 (67.167)
(67.167)
Nous remarquons donc que les valeurs d'amortissement
ne nécessitent pas de connaître le taux de manière
explicite. Il suffit de connaître la valeur finale et initiale.
C'est justement pour cela que la fonction DB( ) de la version française
de Microsoft Excel 11.8346 ne demande pas le taux
d'amortissement.
À remarquer que ce taux constant ainsi que
la valeur finale sont parfois imposés par la législation
dans certains pays (comme c'est le cas en Suisse par exemple) jusqu'à une
valeur résiduelle
nulle ou non nulle elle aussi définie par la législation!
Remarque: L'amortissement géométrique dégressif
convient particulièrement aux biens ayant une très
forte dépréciation les premières années.
CHOIX
D'INVESTISSEMENTS
Par définition, un investissement
est l'acquisition
ou le développement d'un bien (quelle que soit sa forme,
matérielle
ou non) par une entreprise, une collectivité ou un individu.
Un investissement implique dans
le
cadre économique
simple:
1. Une dépense immédiate,
payable en une ou plusieurs fois
2. Des entrées futures,
appelées "cash-flows"
3. Une valeur résiduelle
Il existe plusieurs critères
et techniques pour les choix d'investissements, que nous présenterons
ci-après,
qui permettent d'opter
pour un investissement A ou B: celui de la
"valeur actuelle nette" (VAN),
celui du "taux
interne de rentabilité"
(TRI) ou encore celui de "délai
de récupération" (DR) appelé aussi "délai
de recouvrement".
Remarque: Il ne faut pas oublier aussi que les techniques
de décisions
(cf. chapitre de Théorie Des Jeux
Et De La Décision)
ont une énorme importance lorsque les sommes considérées
atteignent des valeurs non négligeables.
VALEUR ACTUELLE
NETTE
Comme nous l'avons spécifié
plus haut, un investissement implique trois points.
Ce qui intéresse bien évidemment l'investisseur,
c'est
qu'en valeur actuelle, l'investissement rapporte plus que ce qui
est dépensé.
Voyons une situation-type:
Une entreprise souhaite acquérir une nouvelle machine valant
6'000.-, ce qui devrait permettre d'abaisser les coûts de
production de 1'000.- durant 5 ans. Nous estimons que dans 5
ans,
la valeur résiduelle de cette machine sera de 3'000.-. Doit-on
acheter cette machine si cet investissement peut être financé
par un emprunt à 10%?
Quelles informations avons-nous
ici?
1. La dépense immédiate

2. La valeur finale ou résiduelle
du bien d'équipement après 5 ans 
3. Les cash-flows de chaque
année  (qui sont constants sur toute la période dans cet exemple)
(qui sont constants sur toute la période dans cet exemple)
4. Le taux d'intérêt
(taux géométrique moyen du marché)
de l'emprunt correspondant 
Quelles informations, ou
questions intéressantes, financièrement parlant,
pouvons-nous poser par rapport aux données ci-dessus?:
1. Quel serait le capital
initial qui au taux du marché nous permettrait de retirer
1'000.- par année pendant 5 ans (jusqu'à ce que
l'on solde le compte)?:
 (67.168)
(67.168)
ce qui s'écrit si
 (nous retrouvons la relation de la rente certaine postnumerando
vue dans le chapitre d'Économie):
(nous retrouvons la relation de la rente certaine postnumerando
vue dans le chapitre d'Économie):
 (67.169)
(67.169)
Dans notre exemple cette
somme (après un petit calcul) revient à environ
3'790.-.
En d'autres termes, il nous
suffirait de mettre en épargne 3'790.- pendant les mêmes
5 ans, pour en retirer 1'000.- par année jusqu'à solder
le compte. Donc pour l'instant, un investissement de 3'790 pour
économiser (gagner) 1'000.- par année semble beaucoup
plus favorable qu'en dépenser 6'000.- pour le même
retour, sur la même durée...
Déjà là, nous pouvons dire que l'achat de
la machine est défavorable.
Mais il ne faut pas oublier
aussi un deuxième facteur... la valeur résiduelle
de notre machine!!!
2. Quel serait le capital
initial qui au taux du marché nous rapporterait une valeur
équivalente à la valeur résiduelle de notre
machine (c'est une valeur immobilisée au même
titre qu'une épargne, donc nous pouvons nous intéresser à
ce qu'il adviendrait si cette somme provenait d'une épargne)
?
 (67.170)
(67.170)
Dans notre exemple, cette
somme revient environ à 1'862.-
En d'autres termes, il nous suffirait de mettre en épargne
1'862.- pendant les mêmes 5 ans, pour obtenir une somme égale
à la valeur résiduelle de notre machine. Et alors?
Eh bien la conclusion est assez simple.... La somme:
 (67.171)
(67.171)
représente le retour sur la base d'une épargne initiale
pour obtenir, par rapport aux informations de valeur résiduelle
et de cash-flow, la somme finale équivalent à l'achat
de notre machine. Or, dans cet exemple, cette somme nous donne environ
5'652.-.
Ce résultat est important car il est à comparer
avec l'investissement que nous voulions faire initialement. Deux
options
s'offrent donc à nous:
1. Acheter la machine à
6'000.- avec les cash-flows et les valeurs résiduelles que
nous connaissons
2. Épargner 5'652.- pendant
la même période, avec les mêmes cash-flows pour
nous retrouver avec une épargne finale qui devrait être équivalente
à celle de la valeur résiduelle de notre machine.
Or, que pouvons-nous conclure
de notre exemple? Eh, bien simplement que nous nous trouvons dans
un cas défavorable si:
 (67.172)
(67.172)
Soit, explicitement:
 (67.173)
(67.173)
Dans la version française de Microsoft Excel
14.0.7106, il suffit d'écrire (l'écriture est un peu traître):
=-6000+VAN(10%;1000;1000;1000;1000;4000)=-346.60.-
En d'autres termes, pour
le financier (ou chef de projet), le calcul intéressant à faire
est le suivant:
 (67.174)
(67.174)
qui:
1. Lorsqu'il est négatif correspond à un investissement
qu'il vaut mieux éviter
2. Lorsqu'il est nul est un investissement indécidable
3. Lorsqu'il est positif est un bon investissement
Dans certains cas scolaires et livres de gestion de projets, la
relation de la VAN ci-dessus est simplifiée, car ils supposent
que seul un investissement... est fait en début de projet.
Ainsi, nous avons:
 (67.175)
(67.175)
Enfin, précisons que le rapport:
 (67.176)
(67.176)
est souvent appelé "coefficient
d'actualisation"
de la n-période.
Ainsi, la VAN est utilisée comme critère décisionnel
dans les grandes entreprises pour chiffrer l'apport spécifique
d'un projet au résultat
financier de l'entreprise, en tenant compte du coût du capital
utilisé via le taux d'actualisation.
Donc dans le cas d'un choix entre plusieurs investissements, nous
choisirons celui dont la VAN est la plus grande. Si les cash-flows
sont non déterministes il faudra alors calculer l'espérance
et la variance de la VAN. Les spécialistes abrègent
souvent le calcul de l'espérance de la VAN par l'abréviation
VANe pour "valeur actuelle nette espérée"
ou plus fréquemment en anglais "expected
net present value" (eN.P.V.) ou encore "risk-adjusted
net present value" (rN.P.V.). Le lecteur pourra trouver
un exemple de calcul de VANe dans le serveur d'exercice (sinon,
sur demande, nous intégrerons directement l'exemple sur
la présente
page).
Remarque: La VAN est aussi souvent appelée "quasi-rente
actualisée" ou encore en anglais "net
present value" (N.P.V.). Nous trouvons également
souvent la dénomination "méthode
des cash-flows actualisés".
Si nous considérons en avenir certain avec un investissement
initial unique de 10'000.- avec un taux d'actualisation constant
de 10%
et un cash-flow parfaitement périodique de 3'250.-, 3'750.-,
4'250.-, 4'750.- nous avons la représentation tabulaire
traditionnelle:
|
Année |
Action |
Cash-Flow |
C.A. |
C.F.A. |
0
|
Investissement |
-10'000 |
1 |
-10'000 |
|
1 |
Entrée |
3'250 |
0.909 |
2'955 |
|
2 |
Entrée |
3'750 |
0.826 |
3'099 |
|
3 |
Entrée |
4'250 |
0.751 |
3'193 |
|
4 |
Entrée |
4'750 |
0.683 |
3'244 |
|
SOMME |
F.N.T: |
6'000 |
F.N.T.A: |
2'491 |
Tableau: 67.12
- Actualisation détaillée sous forme comptable
où dans le tableau ci-dessus F.N.T. signifie "Fond
Net de Trésorerie" ("net cash flow" en anglais),
F.N.T.A. "Fond
Net de Trésorerie Actualisé",
C.A. "Coefficient d'Actualisation" et
C.F.A. "Cash-Flow
Actualisé".
Ainsi dans ce tableau, l'investissement rapporte 2'491.- de plus
qu'une opération de placement à 10% après
4 ans en avenir certain (univers déterministe).
Nous remarquerons au passage qu'à partir de la 3 année,
l'investissement initial est remboursé. Nous parlons alors
de "période de payback".
TAUX DE RENTABILITÉ
INTERNE
Définition (technique): Le "taux
de rentabilité interne" (TRI), appelé aussi
parfois
"taux limite de rentabilité" ou
"efficacité marginale du capital" est le taux
d'actualisation t% pour lequel la
valeur actualisée
des rentrées
nettes de fonds résultant
d'un projet d'investissement est égale à la valeur
actualisée des décaissements requis pour réaliser
cet investissement.
Pour citer la définition selon J.M. Keynes: l'efficacité marginale
du capital est le taux d'escompte qui, appliqué à la
série
d'annuités
constituée
par les rendements escomptés de ce capital pendant son existence
entière, rend la valeur actuelle des annuités égale
au prix d'offre de ce capital.
En d'autres termes, cela revient à se demander quel est
le taux moyen géométrique du marché pour lequel
la V.A.N. du projet est nulle. Soit à satisfaire la relation:
 (67.177)
(67.177)
qui ne peut que se calculer rapidement avec des outils informatiques
(l'outil Cible dans Microsoft Excel 11.8346 par exemple)
ou plus simplement en utilisant la fonction TRI( ) intégrée dans
presque tous les tableaux (donc Microsoft Excel).
Si le taux de rendement interne est trop faible, le placement
sur les marchés financiers (spéculation) est plus intéressante
alors que l'investissement industriel (ceci est cependant une situation
relativement dangereuuse et qui doit être corrigé par
les banques centrales).
 Exemple: Exemple:
Un ami nous propose de vendre votre machine pour un investissement
de 2'000.- (correspondant à sa valeur résiduelle)
dans un projet ayant un cash-flow qui double chaque période
sur une base de 400.- assurée pendant 3 périodes
alors que le taux moyen géométrique d'intérêt
du marché est de 5%. Lee TRI (taux de rendement
interne) à partir duquel le VAN est nul est donné avec la
version française de Microsoft Excel
14.0.7106:
=TRI({-2000;400;800;1600)=15.117%
Donc entre deux investissements,
nous choisissons dans les entreprises celui dont le TRI est le
plus élevé et
satisfaisant aux contraintes politiques et économiques internes.
Ce type de calcul s'applique donc sur le retour sur projets contre
investissements sur le marché et non pas au retour sur projets
contre exploitation. Ainsi, il s'agit d'un outil calculatoire d'aide
à la décision purement financier et non industriel
ou commercial.
DÉLAI
DE RÉCUPÉRATION ET D'AMORTISSEMENT
Le "délai de récupération" (DR),
appelé aussi "délai de
recouvrement" ou "pay
back" (en
anglais) est un autre indicateur pour l'aide à la décision
dans le cadre des choix d'investissements de projets et plus
simple
à l'utilisation (et à la compréhension) que
la VAN.
Cet indicateur a pour simple et seul objectif de montrer quand,
dans le temps, l'investissement sera remboursé. En d'autres
termes, il indique le nombre de périodes nécessaires
pour que la somme des cash-flows couvre l'investissement initial.
C'est une information très simple à déterminer
qui revient à chercher le plus petit entier p tel
que:
 (67.178)
(67.178)
ou encore:
 (67.179)
(67.179)
En d'autres termes, c'est le moment d'un projet où les
cash-flows
équilibrent l'investissement initial.
Définition: Le "délai
d'amortissement" est
le nombre de périodes
nécessaires tel que:
 (67.180)
(67.180)
ou encore:
 (67.181)
(67.181)
THÉORIES DES FILES D'ATTENTE
Les théories des files d'attente sont des outils extrêmement
puissants et vastes (une présentation complète nécessite
au bas mot 300 pages A4) permettant de prendre en compte et de
modéliser
les goulots d'étranglement
dans les processus des entreprises soit au niveau de la logistique,
des centrales téléphoniques, des requêtes
sur les serveurs, des caisses de grands magasins ou encore dans
les
toilettes des grands
stades sportifs
(...) en fonction des hypothèses et contraintes de départ.
Généralement, les clients voient évidemment
dans l'attente
une activité sans valeur ajoutée et,
s'ils attendent trop longtemps, ils associent cette perte de temps à une
mauvaise qualité de service. De la même
façon, au sein de l'entreprise,
des employés inoccupés ou des équipements
inutilisés représentent des
activités sans valeur ajoutée. Pour éviter
ces situations, la majorité des entreprises
ont mis en place des processus d'amélioration
continue dont le but ultime est l'élimination de toute
forme de gaspillage, notamment l'attente. Tous
ces exemples révèlent l'importance
de l'analyse des files d'attente. A remarquer qui si une entreprise
ou administration n'a pas les moyens financiers ou intellectuels
de faire de la théorie des files d'attentes, le respect minimum
envers les clients est au moins d'indiquer à l'aide d'un affichage
peu onéreux,
le temps d'attente ou de mettre à disposition des moyens de
distractions (télévision, journaux ou magazines)!
Système |
Clients |
Service |
Comptoir-réception |
Personnes |
Réceptionnistes |
Atelier de réparation |
Machines |
Techniciens |
Garages |
Camions |
Mécaniciens |
Hôpital |
Patients |
Infirmiers |
Ordinateur |
Tâches |
Processeurs, disques, rubans |
Aéroport |
Appareils |
Pistes d'envols |
Réseau routier |
Véhicules |
Feux de circulation |
Atelier de fabrication |
Tâches |
Machines/Ouvriers |
Téléphone |
Appels |
Échangeurs |
Transport en commun |
Voyageurs |
Autobus/Métros |
Buanderie |
Lignes |
Laveuses/Sécheuses |
... |
... |
... |
Tableau: 67.13 - Exemples de files d'attente typiques
Ces théories
se révèlent
notamment utiles pour justifier des investissements, des embauches
ou des achats
d'équipements. De façon plus générale,
elle est une partie intégrante
des techniques mathématiques
de gestion lorsqu'il est nécessaire de rechercher un optimum économique
entre des coûts d'attente et des coûts de service d'un
système.
La problématique type dans les entreprises peut s'exprimer ainsi:
- Quel est le nombre optimal de stations/terminaux à mettre en
service permettant de traiter la demande tout en évitant une file
d'attente trop importante et le départ de certains clients?
- Quel est le temps d'attente moyen d'un client/employé devant
la station/terminal?
- Quel est le nombre moyen de clients en attente dans la file?
Ces questions permettent d'exprimer des objectifs en matière
de qualité et de niveau de service:
1. Un temps d'attente moyen ou médian dans le service ou dans
la file à ne
pas dépasser
2. Une probabilité d'attente maximale
3. Un nombre de clients moyen en attente donné
En pratique, lorsque le client est externe à l'entreprise,
le coût d'attente est difficile à
évaluer, car il s'agit d'un impact plutôt
que d'un coût pouvant être comptabilisé. Cependant,
on peut considérer les temps d'attente
comme un critère de mesure du niveau de service.
Le gestionnaire décide du temps d'attente
acceptable et il
met en place la capacité susceptible de fournir ce
niveau de service.
Lorsque le client est interne à l'entreprise, nous pouvons établir
directement certains coûts se rapportant au
temps d'attente des clients (machines). Par ailleurs, il ne faut
pas conclure trop rapidement que pour l'entreprise,
le coût du temps
d'attente d'un employé qui attend est égal à son
salaire durant le temps d'attente. Cela impliquerait que la baisse
nette des gains de l'entreprise, du fait de l'inactivité d'un
employé, est égale au salaire de ce
dernier, ce qui, a priori, n'est pas évident. L'employé,
qu'il travaille ou qu'il attende, reçoit
le même salaire. Par contre, sa contribution
aux gains de l'entreprise est réellement perdue,
car la productivité baisse. Quand un opérateur
de machine est inactif parce qu'il attend, sa
force productive (qui peut comprendre, outre son salaire, une
proportion des coûts
fixes de l'entreprise) est perdue. En d'autres termes, il
faut tenir
compte non pas de la ressource physique en attente, mais plutôt
de la valeur (coût) de toutes les ressources économiques
inactives, et évaluer
ensuite la perte de profit à partir de la perte
de productivité. L'objectif de l'analyse
des files d'attente est
de trouver un compromis entre le coût
associé à la capacité de service et le coût
d'attente des clients.
Ces théories font donc appel à des méthodes statistiques
et algébriques
que nous avons étudiées dans les chapitres de Statistiques
et de Théorie Des Graphes. Elles n'en sont alors que plus
passionnantes.
Pour présenter le sujet, plutôt que de faire une généralisation
abstraite, nous avons choisi de développer la théorie
autour d'un exemple concret et classique qui est le télétrafic.
Une généralisation
à tout autre cas d'étude se faisant ensuite relativement
facilement par analogie.
Considérons donc une centrale téléphonique
regroupant les lignes d'un ensemble d'immeubles d'une ville et
ne possédant pas autant
de lignes allant vers le réseau que de lignes allant vers
les différents
particuliers qu'il dessert.
Nous pouvons donc légitiment nous demander de combien de lignes
nous avons besoin pour desservir tous ces abonnés.
Pour dimensionner son réseau, un opérateur va devoir calculer
le nombre de ressources à mettre en oeuvre pour qu'avec une probabilité
extrêmement proche de 1, un usager qui décroche son téléphone puisse
disposer d'un circuit. Pour cela, il va falloir développer quelques
relations de probabilité de blocage. Ces relations vont demander
une modélisation statistique des instants de début et de fin d'appels
ainsi que des durées de ces appels. Les paragraphes qui suivent
vont donc introduire les lois de probabilités utilisées pour ces
dimensionnements.
Enfin, avant de commencer, nous souhaitons mettre à disposition
le tableau récapitulatif ci-dessous des notations les plus importantes
que le lecteur découvrira au fur et à mesure de sa lecture et auquel
il pourra se reporter en cas de confusion:
Variables |
Information |
Unité |

|
Flux d'arrivée de clients dans
la file d'attente (communication), appelé également "taux
moyen d'arrivée des appels", ou encore "fréquence
moyenne d'arrivées".
L'inverse  donne
le temps moyen entre arrivées (appels) dans la file d'attente. donne
le temps moyen entre arrivées (appels) dans la file d'attente. |

|

|
Flux de départ de clients (communication)
correspondant au taux de traitement. L'inverse  donne
le temps moyen d'attente pendant le service (donc une fois
arrivé en fin de file d'attente) appelé aussi "temps
moyen de service". donne
le temps moyen d'attente pendant le service (donc une fois
arrivé en fin de file d'attente) appelé aussi "temps
moyen de service". |

|
A ou  |
Taux d'utilisation du service
(par unité de serveur). Assimilé au concept de trafic (un
peu abusivement) ou de charge. Est égal au rapport  et
doit être strictement inférieur à 1 pour éviter l'engorgement. et
doit être strictement inférieur à 1 pour éviter l'engorgement. |
- |
C |
Nombre de clients au total
dans le système |
- |

|
Nombre de clients en attente
dans la queue |
- |

|
Nombre de clients en service
(traitement) |
- |
T |
Temps d'attente dans le système |
[s] |

|
Temps d'attente dans la queue |
[s] |

|
Probabilité d'avoir k clients
dans le système |
- |
Tableau: 67.14 - Notations conventionnelles des files d'attente
et précisons que les paramètres à prendre en compte son souvent:
- Le type de processus d'arrivée des clients (données)
- La distribution statistique du temps de service (traitement)
- Le nombre de caisses (serveurs)
- La capacité du système (souvent supposée infinie dans la pratique...)
- La taille de la population
- Le discipline du service
MODÉLISATION DES DURÉES D'ARRIVÉES M/M/...
Dans ce modèle M/M/... dont nous expliquerons
l'origine de la notation plus tard, nous considérons des
appels qui débuteraient de manière
aléatoire.
Prenons ensuite un intervalle de temps t et divisons cet
intervalle en n sous-intervalles de durée t/n.
Nous choisissons n suffisamment grand pour que les hypothèses
suivantes soient respectées:
H1. Une seule arrivée d'appel peut survenir dans un intervalle
t/n
H2. Les instants d'arrivée d'appels sont indépendants
les uns des autres (le taux d'arrivée n'est pas influencé par
le nombre d'appels provenant de la population). Ce qui présuppose
une population infinie.
H3. La probabilité qu'un appel arrive dans un sous-intervalle
donné est proportionnelle à un facteur constant près à la
durée
du sous-intervalle.
Nous écrivons alors la probabilité de un appel  dans
un sous-intervalle (1) de la manière suivante: dans
un sous-intervalle (1) de la manière suivante:
 (67.182)
(67.182)
où le 1 en indice du p représente donc l'analyse sur 1
appel, le 1 entre parenthèses le fait que l'analyse se fait sur
1 sous-intervalle et enfin le terme  représente
le coefficient de proportionnalité entre la probabilité et la durée
t/n du sous-intervalle. représente
le coefficient de proportionnalité entre la probabilité et la durée
t/n du sous-intervalle.
L'hypothèse de départ consistant à considérer
comme nulle la probabilité
d'avoir plusieurs appels dans un sous-intervalle s'écrit
alors:
 (67.183)
(67.183)
La probabilité de n'avoir aucun appel durant un sous-intervalle
de temps t/n s'écrit donc:
 (67.184)
(67.184)
En développant, nous obtenons:
 (67.185)
(67.185)
et en utilisant la propriété énoncée
juste au-dessus:
 (67.186)
(67.186)
La probabilité d'avoir k arrivées d'appels
durant n
intervalles de temps s'obtient alors en considérant le nombre
de manières de choisir k intervalles parmi n...
(puisqu'il ne peut y avoir plus d'un appel par intervalle).
Pour chacune de ces solutions, nous aurons alors forcément k
intervalles avec une arrivée d'appel et n-k intervalles
avec aucune arrivée d'appel. Nous avons vu dans le chapitre
de Statistique que la loi qui permettait d'obtenir la probabilité de
choisir un certain arrangement d'issues binaires parmi un nombre
total d'issues
était la loi de Bernoulli donnée par:
 (67.187)
(67.187)
Il vient donc dans notre cas de figure que la probabilité d'une
des solutions sera:
 (67.188)
(67.188)
La probabilité globale s'obtient en sommant les probabilités
de tous les cas, ce qui nous donne la loi binomiale (cf.
chapitre de Statistiques):
 (67.189)
(67.189)
Ou encore, en remplaçant les probabilités par leurs valeurs en
fonction de  : :
 (67.190)
(67.190)
La limite de la probabilité  lorsque
n tend vers l'infini va être égale à la probabilité d'avoir
k arrivées d'appel durant un intervalle de temps t.
Nous notons lorsque
n tend vers l'infini va être égale à la probabilité d'avoir
k arrivées d'appel durant un intervalle de temps t.
Nous notons  cette
probabilité: cette
probabilité:
 (67.191)
(67.191)
En reprenant alors les différents termes de l'expression
de  , il
vient: , il
vient:
 (67.192)
(67.192)
En utilisant les développements de Taylor (cf.
chapitre de Suites Et Séries):
 (67.193)
(67.193)
Soit en ne prenant que le premier terme, c'est-à-dire en
considérant
x très petit:
 (67.194)
(67.194)
Donc:
 (67.195)
(67.195)
et pour la dernière partie:
 (67.196)
(67.196)
d'où après regroupement:
 (67.197)
(67.197)
Cette fonction de distribution est donc extrêmement importante,
car elle représente
la probabilité
d'observer k arrivées d'appels dans un intervalle
de durée
t (ou le nombre de clients qui se trouvent devant une caisse
dans un intervalle de durée t) et il s'agit donc
d'une distribution de Poisson (cf.
chapitre de Statistiques). Dans la pratique, il faut donc
s'assurer avant d'utiliser les relations qui vont suivre que cette
distribution soit bien respectée (avec un test du Khi-deux
typiquement).
Considérons maintenant la fonction de répartition,
appelée "fonction de répartition
d'Erlang", qui pour un intervalle
de temps t donné donne
la probabilité cumulée d'avoir
un nombre k d'arrivées supérieur ou égal à n:
 (67.198)
(67.198)
Si nous dérivons cette fonction par rapport à t cela
donne la "fonction de distribution d'Erlang" (le
lecteur aura peut-être remarqueé que retrouvons donc dans l'avant-dernière
ligne un exemple pour le mangement du cocnept de "série télescopique"
qui avait été introduction dans la section de Suites et Séries):
 (67.199)
(67.199)
et donc nous retrouvons une forme particulière de la fonction
de distribution de la loi Gamma vue dans le chapitre de Statistiques.
Rappelons au passage l'équivalence déjà présentée
dans le chapitre de Statistiques dans la version française de Microsoft Excel
14.0.6123 entre la loi de Poisson, la loi du
Khi-2 et la loi Gamma:
 (67.200)
(67.200)
Il s'ensuit par analogie avec
la forme générale de la loi de Poisson que le paramètre  est
le taux moyen d'arrivée (taux moyen d'apparition) d'appels
par unité de temps (ou en anglais "Poisson
Arrivals See Time Average": PASTA...).
Typiquement il s'agira d'un nombre moyen d'appels par seconde
(voir les estimateurs
de la loi de Poisson dans le chapitre
de Statistiques). est
le taux moyen d'arrivée (taux moyen d'apparition) d'appels
par unité de temps (ou en anglais "Poisson
Arrivals See Time Average": PASTA...).
Typiquement il s'agira d'un nombre moyen d'appels par seconde
(voir les estimateurs
de la loi de Poisson dans le chapitre
de Statistiques).
Ainsi, nous avons pour espérance et variance (cf.
chapitre de Statistiques) du nombre d'appels:
 (67.201)
(67.201)
 Exemple: Exemple:
Une TPE souhaitant mettre en place une hotline estime qu'au
début elle recevra par journée de 8 heures, 4 appels
téléphoniques (soit une probabilité de 1 chance
sur 2 d'avoir un appel par heure et donc un taux moyen  de
0.5 appels par heure). Alors la probabilité qu'elle
reçoive exactement 4 appels (k) par jour et au
moins 4 appels (k) par jour selon le modèle théorique
de la théorie
des files d'attente est de: de
0.5 appels par heure). Alors la probabilité qu'elle
reçoive exactement 4 appels (k) par jour et au
moins 4 appels (k) par jour selon le modèle théorique
de la théorie
des files d'attente est de:
 (67.202)
(67.202)
où nous avons utilisé la fonction POISSON( ) intégrée
dans la version française de Microsoft Excel 14.0.6123.
Maintenant, introduisons la variable aléatoire  représentant
le temps séparant deux arrivées d'appel. Nous définissons
pour cela la probabilité A(t)
qui est la probabilité que le temps représentant
le temps séparant deux arrivées d'appel. Nous définissons
pour cela la probabilité A(t)
qui est la probabilité que le temps  soit
inférieur ou égal à une valeur t: soit
inférieur ou égal à une valeur t:
 (67.203)
(67.203)
Nous avons donc:
 (67.204)
(67.204)
Or,  représente
la probabilité cumulée qu'il n'y ait aucune arrivée
d'appels durant un temps
t. Cette probabilité cumulée a justement été établie
plus haut: représente
la probabilité cumulée qu'il n'y ait aucune arrivée
d'appels durant un temps
t. Cette probabilité cumulée a justement été établie
plus haut:
 (67.205)
(67.205)
Nous en déduisons:
 (67.206)
(67.206)
Il s'agit donc de la fonction de répartition d'une loi exponentielle!
Nous pouvons aussi introduire la densité de probabilité de
la variable aléatoire .
Nous obtenons ainsi: .
Nous obtenons ainsi:
 (67.207)
(67.207)
Remarque: Rappelons
que dans le chapitre de Statistiques, nous avons souvent fait la
démarche inverse. C'est-à-dire compte tenu
d'une densité de probabilité a(t) nous
cherchions la fonction de répartition A(t) via
une intégration
sur le domaine de définition de la variable aléatoire.
La densité de probabilité permet donc de calculer la durée moyenne
entre deux arrivées d'appel:
 (67.208)
(67.208)
En intégrant par parties, il vient:
 (67.209)
(67.209)
Nous obtenons ainsi, que pour un taux d'arrivée
de  appels
par seconde, le temps moyen entre appel est égal à appels
par seconde, le temps moyen entre appel est égal à  (résultat
relativement logique mais encore fallait-il le démontrer
rigoureusement). Effectivement, si nous avons (résultat
relativement logique mais encore fallait-il le démontrer
rigoureusement). Effectivement, si nous avons  qui
vaut 2 appels par heure, le temps moyen d'arrivée est bien
de 0.5 heures (1/2) entre appels. qui
vaut 2 appels par heure, le temps moyen d'arrivée est bien
de 0.5 heures (1/2) entre appels.
Supposons maintenant qu'aucun appel ne soit arrivé jusqu'à un
temps  et
que nous souhaitions calculer la probabilité qu'un appel
arrive durant une durée t après le temps et
que nous souhaitions calculer la probabilité qu'un appel
arrive durant une durée t après le temps  . .
Nous devons donc calculer la probabilité d'avoir une durée entre
deux appels inférieure à  tout
en étant supérieure à tout
en étant supérieure à  . .
Cette probabilité s'écrit  .
En utilisant la formule de Bayes (cf. chapitre
de Probabilités): .
En utilisant la formule de Bayes (cf. chapitre
de Probabilités):
 (67.210)
(67.210)
mais avec les notations idoines, il vient:
 (67.211)
(67.211)
Cette probabilité peut encore s'écrire:
 (67.212)
(67.212)
En reprenant les expressions des différentes probabilités:
 (67.213)
(67.213)
Nous voyons donc que la probabilité d'apparition d'un appel
durant un temps t après une durée  pendant
laquelle aucun n'est arrivé est la même que la probabilité d'apparition
d'un appel pendant une durée t, indépendamment de ce qui
a pu arriver avant. Nous considérons donc que le phénomène (la loi
exponentielle) est sans mémoire. pendant
laquelle aucun n'est arrivé est la même que la probabilité d'apparition
d'un appel pendant une durée t, indépendamment de ce qui
a pu arriver avant. Nous considérons donc que le phénomène (la loi
exponentielle) est sans mémoire.
MODÉLISATION DES DURÉES DE SERVICE M/M/...
Dans ce modèle M/M/... dont nous expliquerons
encore une fois l'origine de la notation plus tard, nous allons
étudier les lois de probabilité qui modélisent
les durées
des appels (sous-entendu: en service une fois la fin de la file
d'attente atteinte). Pour cela, nous procédons
comme précédemment.
Nous considérons donc un intervalle de temps de durée t
que nous décomposons en n sous-intervalles de durée t/n.
Nous choisissons n de sorte que les hypothèses suivantes
restent justifiées:
H1. La probabilité qu'un appel se termine durant un sous-intervalle
est proportionnelle à la durée du sous-intervalle.
Nous noterons:
 (67.214)
(67.214)
cette probabilité, expression dans laquelle  représente
le coefficient de proportionnalité. représente
le coefficient de proportionnalité.
H2. La probabilité qu'un appel se termine durant un sous-intervalle
est indépendant du sous-intervalle considéré.
Nous introduisons alors la variable aléatoire  représentant
la durée d'un appel et la probabilité H(t)
que la durée d'un appel soit inférieure ou égale à t: représentant
la durée d'un appel et la probabilité H(t)
que la durée d'un appel soit inférieure ou égale à t:
 (67.215)
(67.215)
La probabilité qu'un appel ayant débuté à t = 0 ne se termine
pas avant t s'écrit alors:
 (67.216)
(67.216)
Cette probabilité est égale à la probabilité que
l'appel ne se termine dans aucun des n sous-intervalles
de durée t/n:
 (67.217)
(67.217)
En faisant tendre n vers l'infini, nous obtenons:
 (67.218)
(67.218)
Nous obtenons donc l'expression de la probabilité qu'un appel
ait une durée inférieure ou égale à t:
 (67.219)
(67.219)
Nous pouvons en déduire la densité de probabilité associée, notée
h(t):
 (67.220)
(67.220)
qui correspond donc à une loi exponentielle (le temps
qu'un client emploie pour être servi à une
caisse - durée de service - ou pour que son appel soit traité une
fois en fin de file d'attente suit donc une loi exponentielle!).
Dans la pratique, il faut donc s'assurer avant d'utiliser les relations
qui vont suivre que cette
distribution soit bien respectée (avec un test du Khi-deux
typiquement).
De la même manière que dans les paragraphes précédents,
la durée
moyenne d'appel (laps de temps moyen entre deux fins d'appels en
service) s'obtient en calculant (toujours la même intégration
par parties que plus haut):
 (67.221)
(67.221)
En conclusion, nous avons  appels
qui cessent par seconde et nous avons une durée moyenne
d'appel en service égale à: appels
qui cessent par seconde et nous avons une durée moyenne
d'appel en service égale à:
 (67.222) (67.222)
Effectivement, si nous avons par exemple 2 appels en service
qui cessent par heure, cela nous donne une durée moyenne
de 0.5 heure (1/2) de service par appel.
Le rapport:
 (67.223)
(67.223)
représente donc le nombre d'appels qui apparaissent dans
la file d'attente sur le nombre d'appels en service qui se terminent
pendant un intervalle de temps (temps de service moyen), c'est-à-dire
qui représente
en fait tout simplement le trafic (ou autrement dit: l'intensité de
trafic) ou d'un autre point de vue l'utilisation moyenne du service
dont l'unité est le "Erlang"
(nous rappellerons cette définition plusieurs fois par la
suite...).
 Exemple: Exemple:
Dans un magasin, on compte 240 clients par heure et il faut 28
secondes en moyenne pour traiter un client (temps de service moyen).
Sachant que la durée de service suit une loi exponentielle
et la distribution des arrivées une loi de Poisson, quelle
est l'intensité du
trafic et le taux d'occupation des caisses si le magasin n'en a
que deux?
Le trafic est donc donné par le nombre de clients
par heure divisé par le nombre de clients traités par heure. Comme
il faut 28 secondes pour en traiter un et qu'il y a 3'600 secondes
dans une heure, nous avons l'intensité de trafic suivante:
 (67.224)
(67.224)
La charge moyenne (ou taux d'occupation) par caisse, sachant
qu'il y en a deux, est donc de:
 (67.225)
(67.225)
C'est cette dernière valeur qui sera prise au final comme valeur
du trafic A par station pour les calculs ultérieurs.
Les probabilités d'apparition d'appels et de fin d'appels qui
ont été développées dans les paragraphes précédents permettent de
modéliser le processus complet d'apparition et de fin d'appels.
NOTATION DE KENDALL
Une notation a été développée par Kendall pour représenter les
files d'attente suite aux développements intensifs (et nombreux)
des modèles
mathématiques les concernant. La forme réduite de cette notation
est:
A/B/C
où A représente le processus d'arrivée des
clients dans le système (loi de distribution), B représente
la distribution du temps de service des clients du système
(loi de distribution) et C le
nombre de serveurs du système.
Par exemple, la notation M/M/1 signifie que les
clients arrivent dans le système selon une loi de Poisson
modélisée
par une chaîne de Markov (cf. chapitre
de Probabilités), que le temps de traitement suit
une distribution de type exponentiel (modélisé par
une chaîne
de Markov aussi) et le système
constitué d'un seul serveur selon le principe du premier
arrivé premier
servi dans une file d'attente à population infinie et régime
permanent. Ce qui correspond respectivement aux trois relations
suivantes
que nous avons démontrées plus haut pour la probabilité d'arrivée
de k appels dans un temps donné:
 (67.226)
(67.226)
la probabilité que le temps de traitement (temps de service)
soit égale à une certaine valeur:
 (67.227)
(67.227)
et la probabilité d'avoir k clients (communications):
 (67.228)
(67.228)
La lettre M est utilisée pour indiquer que les processus
employés sont du type markovien (sous-entendu exponentiels).
En général, nous utilisons la notation:
A/B/C/d:e
d représentant le nombre maximum de clients pouvant être
présents simultanément dans le système. Ce
nombre entier varie entre 1 et l'infini. Quand la capacité mémoire
de la file est considérée
comme illimitée, ce paramètre est souvent omis. Quant
à e, il représente la discipline de service.
Par exemple:
- FIFO pour premier arrivé, premier servi (First In-First
Out appelé aussi FCFS pour First Come-First Serve). Tous les modèles
théoriques que nous allons développer ci-dessous seront de type
FIFO!
- LIFO pour dernier arrivé premier servi (Last In-First Out appelé aussi
LCFS pour Last Come-First Serve)
- SJF pour servir le travail le plus court d'abord (Shortest
Job First)
- SRO pour servir en ordre aléatoire (Service in Randon Order)
et encore d'autres...
Ce dernier paramètre est omis si la discipline est FIFO. Ainsi, M/M/1
s'écrirait sans rien omettre:

On trouve également des variantes dans la littérature
de la définition ci-dessus ce qui n'aide pas toujours à la lecture...
MODÉLISATION DES ARRIVÉES ET DÉPARTS M/M/1
À chaque instant un certain nombre d'appels vont apparaître
et d'autres vont se terminer. Nous pouvons donc modéliser
l'état où
l'on se trouve à un instant donné comme une chaîne d'états.
Chaque état représente le nombre d'appels
en cours. Nous concevons donc bien que si, à un instant
donné,
il y a k
appels, nous ne pouvons passer que dans deux états adjacents
selon nos hypothèses: k-1 et k+1.
Nous reconnaissons alors une chaîne de Markov (cf.
chapitre de Probabilités). La probabilité de
passer d'un
état i à un état j pendant un temps dt sera
donc notée:
 (67.229)
(67.229)
Nous introduisons alors les probabilités de transition d'état
suivantes:
- Étant dans l'état k, la probabilité  pour
passer à l'état k + 1 durant un intervalle de temps dt
sera notée pour
passer à l'état k + 1 durant un intervalle de temps dt
sera notée 
- Étant dans l'état k, la probabilité  pour
passer à l'état k-1 durant un intervalle de temps dt
sera notée pour
passer à l'état k-1 durant un intervalle de temps dt
sera notée 
- Étant dans l'état k + 1, la probabilité  pour
passer à l'état k durant un intervalle de temps dt
sera notée pour
passer à l'état k durant un intervalle de temps dt
sera notée 
- Étant dans l'état k - 1, la probabilité  pour
passer à l'état k durant un intervalle de temps dt
sera notée pour
passer à l'état k durant un intervalle de temps dt
sera notée 

Figure: 67.30 - Schéma de principe
Les grandeurs  et et
 sont
des taux d'arrivée (apparition) et de départ (fin) d'appels du même
type que ceux utilisés lors des paragraphes précédents. La seule
différence tient au fait que ces taux ont en indice l'état où se
trouve le système. sont
des taux d'arrivée (apparition) et de départ (fin) d'appels du même
type que ceux utilisés lors des paragraphes précédents. La seule
différence tient au fait que ces taux ont en indice l'état où se
trouve le système.
Nous pouvons alors introduire la probabilité d'état,
c'est-à-dire
la probabilité d'être dans un état k à un
instant t.
Notons pour cela  cette
probabilité (à rapprocher de la notation cette
probabilité (à rapprocher de la notation  utilisée
pour les chaînes de Markov à temps discret dans le chapitre de
Probabilités). utilisée
pour les chaînes de Markov à temps discret dans le chapitre de
Probabilités).
La variation de cette probabilité durant un intervalle
de temps
dt est alors égale à la probabilité de rejoindre
cet état
en venant d'un état k-1 ou d'un état k+1
moins la probabilité
de quitter cet état pour aller vers un état k-1
ou vers un
état k+1.
Ce qui s'écrit:
 (67.230)
(67.230)
En supposant le système stable, c'est-à-dire en supposant qu'il
se stabilise sur des probabilités d'état fixes lorsque le temps
tend vers l'infini, nous pouvons écrire que:
 (67.231)
(67.231)
Nous pouvons alors noter  d'où
finalement: d'où
finalement:
 (67.232)
(67.232)
Nous aurions pu introduire cette dernière relation d'une autre
manière: Elle exprime simplement le fait que la probabilité de
partir d'un état est égale à celle pour y arriver (c'est peut-être
plus simple ainsi).
Cette relation est vérifiée pour tout  avec
les conditions mathématiques suivantes (car sinon ces termes
n'ont aucun sens mathématique): avec
les conditions mathématiques suivantes (car sinon ces termes
n'ont aucun sens mathématique):
 (67.233)
(67.233)
et la condition logique réelle suivante (des appels non encore
existants ne peuvent finir...):
 (67.234)
(67.234)
Remarque: Insistons
sur le fait que la stabilité des probabilités
signifie qu'il y a une probabilité égale de quitter l'état  que
de le rejoindre. que
de le rejoindre. En écrivant le système d'équation précédent,
nous trouvons:
 (67.235)
(67.235)
Nous trouvons alors assez facilement la forme générale:
 (67.236)
(67.236)
Le système se trouvant obligatoirement dans un des états
nous avons la relation suivante qui doit obligatoirement
être respectée:
 (67.237)
(67.237)
En remplaçant avec la relation antéprécédente:
 (67.238)
(67.238)
Ce qui donne aussi:
 (67.239)
(67.239)
et donc:
 (67.240)
(67.240)
Si nous considérons maintenant un système
avec une seule ligne et de capacité infinie (régime
permanent), les grandeurs  (taux
d'arrivée des appels) et (taux
d'arrivée des appels) et  (taux
de départ des appels) auront des valeurs identiques pour
tout k.
C'est-à-dire que nous considérons que le taux d'arrivée
ainsi que le taux de départ sont constants quelle que soit
la position dans laquelle on se trouve dans la file d'attente.
Nous avons alors
la dernière relation qui se simplifie: (taux
de départ des appels) auront des valeurs identiques pour
tout k.
C'est-à-dire que nous considérons que le taux d'arrivée
ainsi que le taux de départ sont constants quelle que soit
la position dans laquelle on se trouve dans la file d'attente.
Nous avons alors
la dernière relation qui se simplifie:
 (67.241)
(67.241)
En utilisant le résultat démontré dans
le chapitre sur les Suites Et Séries (série de Gauss)
nous avons sous des conditions précises nécessaires
de convergence (A doit être strictement plus petit que 1):
 (67.242)
(67.242)
Puisque k représente le nombre d'appels,
cette dernière relation donne la probabilité d'avoir
0 appel (clients) pour un trafic permanent donné A
sur la ligne.
En utilisant:
 (67.243)
(67.243)
nous avons alors en toute généralité pour
ce type de système la
probabilité
d'avoir k appels en régime permanent qui est donné par:
 (67.244)
(67.244)
Il en vient que l'espérance du nombre de communications (clients)
dans le système (dans la queue + en service) est alors par définition
de l'espérance:
 (67.245)
(67.245)
puisque  représente
la probabilité pour qu'il y ait à tout instant k appels
dans le système (file d'attente + en service). Or, nous avons vu
dans le chapitre sur les Suites et Séries que: représente
la probabilité pour qu'il y ait à tout instant k appels
dans le système (file d'attente + en service). Or, nous avons vu
dans le chapitre sur les Suites et Séries que:
 (67.246)
(67.246)
et si q est strictement inférieur à 1 et que n tend
vers l'infini, nous avons immédiatement:
 (67.247)
(67.247)
Si nous dérivons cette dernière relation:
 (67.248)
(67.248)
et en multipliant par q il vient alors:
 (67.249)
(67.249)
Il vient alors au final pour l'espérance du nombre de clients
dans le système:
 (67.250)
(67.250)
Si nous souhaitons connaître l'espérance du nombre de clients
en attente dans la queue uniquement, il faut bien comprendre qu'à chaque
instant nous avons donc une probabilité  qu'il
y ait k clients dans le système mais comme 1 parmi ceux-ci
est alors toujours en service (donc hors de la queue d'attente)
il reste que nous en avons toujours k-1 réellement en attente.
Donc: qu'il
y ait k clients dans le système mais comme 1 parmi ceux-ci
est alors toujours en service (donc hors de la queue d'attente)
il reste que nous en avons toujours k-1 réellement en attente.
Donc:
 (67.251)
(67.251)
Connaissant le nombre de communications (ou de clients) que nous
avons sur l'unique ligne dans tout le système, nous avons alors
l'espérance du temps d'attente (temps d'attente moyen), notée E(T) qui
sera donnée par le rapport de l'espérance du nombre de communications
(clients) en régime permanent sur la ligne E(C) par le taux
d'arrivée des appels.
 (67.252)
(67.252)
Ce résultat, appelé "relation
de Little" (ce
dernier ayant démontré rigoureusement que la relation
est valable pour n'importe quel type de file d'attente), est intuitif
dans
le cas
présent. Effectivement, prenons un appel type au hasard.
Quand il arrive dans le système, il va se trouver statistiquement
face à E(C) en train
d'attendre. Quand il quittera le système, il y aura été un
temps moyen E(T). Donc pendant ce
temps moyen,  appels
seront arrivés derrière lui dans le système.
En régime permanent,
le nombre d'appels laissés derrière lors du départ
doit égaler
le nombre d'arrivées. D'où l'égalité appels
seront arrivés derrière lui dans le système.
En régime permanent,
le nombre d'appels laissés derrière lors du départ
doit égaler
le nombre d'arrivées. D'où l'égalité  dont
on déduit alors immédiatement la relation de Little. dont
on déduit alors immédiatement la relation de Little.
Nous avons alors pour l'espérance du temps d'attente dans le
système:
 (67.253)
(67.253)
Pour déterminer le temps d'attente dans la queue seule, il suffit
de soustraire le temps de traitement/service de par la propriété de
linéarité de la moyenne (durée d'appel moyenne en service):
 (67.254)
(67.254)
Pour résumer, car il y a beaucoup de paramètres et résultats,
nous avons donc pour une file d'attente de type M/M/1 (selon la
notation de Kendall):
Information
|
M/M/1 |
Probabilité système vide |

|
Probabilité d'attente |
A |
Nombre moyen de clients dans
le système |

|
Nombre moyen de clients en
attente |

|
Nombre moyen de clients en
service |
A
|
Temps moyen de séjour dans
le système |

|
Temps moyen d'attente dans
la queue |

|
Condition d'atteinte de l'équilibre |

|
Probabilité d'avoir k clients |

|
Tableau: 67.15 - Résumé des relations importantes d'une file M/M/1
Nous voyons que certaines relations divergents vers l'infini lorsque
le trafic permanent A (rapport des entrées sur) tend vers
l'unité. Raison pour laquelle nous avions imposé plus haut que
ce paramètre soit strictement inférieur à l'unité.
Il faudrait pour chaque type possible de file d'attente faire
les démonstrations détaillées des relations
correspondantes ce qui est long et laborieux (c'est un métier/spécialisation à part
entière et il exixte des ouvrages de plus de 400 pages sur
le sujet).
 Exemple: Exemple:
Supposons que l'on dispose d'une machine à commande numérique
traitant des pièces une à la fois. Supposons que  (nombre
de pièces arrivant en moyenne par heure) et que (nombre
de pièces arrivant en moyenne par heure) et que  (nombre
de pièces sortant en moyenne par heure). Nous avons alors: (nombre
de pièces sortant en moyenne par heure). Nous avons alors:
 (67.255)
(67.255)
ce qui correspond au trafic ou taux d'occupation de la machine.
Donc il y a 20% de probabilité pour que le système
soit vide et 80% de probabilité pour qu'il y ait une attente.
 (67.256)
(67.256)
ce qui correspond donc au nombre moyen de pièces dans le
système
(machine + en attente).
 (67.257)
(67.257)
ce qui correspond donc au nombre moyen de pièces en attente
en dehors de la machine.
 (67.258)
(67.258)
ce qui correspond à un temps moyen de séjour de
30 minutes dans le système.
 (67.259)
(67.259)
ce qui correspond à une attente moyenne de 24 minutes dans
la file d'attente.
Et la probabilité qu'il y a ait 5 pièces dans le système (exécution
+ attente):
 (67.260)
(67.260)
PROBABILITÉ DE MISE EN ATTENTE M/M/k/k (FORMULE
D'ERLANG-B)
Nous allons nous intéresser ici à un système
disposant de N
canaux de communication (chaque canal est censé supporter
un débit de
un appel avec réponse immédiate). Si les N canaux
sont occupés, les appels qui arrivent sont considérés
comme perdus (absence de tonalité
par exemple). Nous parlons alors de blocage ou ruine du système.
Il s'agit donc d'une file d'attente limitée de type M/M/k/k
selon la notation de Kendall, appelée également "système
à perte".
Nous allons chercher à estimer cette probabilité de blocage
en fonction du nombre de canaux disponibles et du trafic.
Compte tenu de ce qui a été énoncé sur
le caractère sans mémoire
du processus d'arrivée d'appels, nous pouvons considérer
que la probabilité:
 (67.261) (67.261)
d'avoir k appels à l'état k est indépendante
de l'état
du système tel que:
 (67.262)
(67.262)
Ainsi, à chaque état k du système
la loi de probabilité
de type Poisson est valable. La différence de traitement
c'est que plutôt que de considérer des états,
nous allons considérer qu'un
canal de communication peut être envisagé comme
un état propre.
Pour la probabilité de fin d'appel, nous avons par contre:
 (67.263)
(67.263)
Effectivement, cette probabilité traduit juste le fait
que si k
appels sont en cours chacun a une probabilité  de
se terminer, d'où la somme qui donne de
se terminer, d'où la somme qui donne  .
Nous avons alors: .
Nous avons alors:
 (67.264)
(67.264)
Ainsi, en injectant ces relations dans:
 (67.265)
(67.265)
il vient:
 (67.266)
(67.266)
En introduisant alors (qui doit être strictement
inférieure à 1 si nous voulons que les développements suivants
convergent vers une valeur finie: chaîne de Markov ergodique):
 (67.267)
(67.267)
qui représente pour rappel le nombre d'appels qui apparaissent
sur le nombre d'appels qui se terminent pendant un intervalle de
temps
(temps de service moyen),
ce qui représente en fait tout simplement le trafic (ou
autrement dit: l'intensité
de trafic), il vient alors:
 (67.268)
(67.268)
ou encore en introduisant le 1 dans la sommation:
 (67.269)
(67.269)
Puisque k représente le nombre d'appels, cette
dernière relation donne la probabilité d'avoir 0
appel (clients) pour un trafic permanent donné A dans
le système.
En reportant  dans
l'expression suivante de dans
l'expression suivante de  (probabilité
d'être dans l'état k donc...) obtenue plus
haut: (probabilité
d'être dans l'état k donc...) obtenue plus
haut:
 (67.270)
(67.270)
il vient:
 (67.271)
(67.271)
et en considérant le caractère sans mémoire,
nous avons la relation:
 (67.272)
(67.272)
Il vient:
 (67.273)
(67.273)
où les k peuvent malheureusement porter à confusion.
Il convient de faire un peu le ménage. Au numérateur,
le k fait
référence au nombre de canaux (serveurs, lignes,
opérateurs ou terminaux) et au dénominateur le N aussi.
Il convient donc de réécrire cela de manière
plus convenable:
 (67.274)
(67.274)
qui donne donc la probabilité de mise en attente (et donc
de saturation/blocage) d'un système
disposant de N
canaux à capacité finie selon le principe du premier/arrivé premier
servi (FIFO: First In/First Out) et pour un trafic A (exprimé donc
en "Erlang") et dans lequel les communications sont perdues
si mises en attente.
Cette relation est parfois notée dans les ouvrages spécialisés
sous la forme:  (67.275)
(67.275)
Cette relation est très importante en théorie des
files d'attente et porte le nom de "formule
d'Erlang-B".

Figure: 67.31 - Probabilité de saturation (plot de la fornction Erlang-B)
Elle est à la base du dimensionnement des
réseaux
à commutation de circuits. En effet, le problème
du dimensionnement d'un commutateur de circuits est le suivant:
Étant donné le trafic
en nombre de communications par unité de temps A en
Erlang, trouver le nombre d'unités de service k tel
que la probabilité qu'un appel arrive dans un système
devenu bloquant soit inférieur à une certaine valeur.
La probabilité obtenue représente
alors la qualité
de service offerte par le réseau du point de vue de l'usage.
Quant au trafic A, il est estimé en fonction du
nombre de postes téléphoniques existants et/ou à venir
sur la base d'une activité
moyenne par poste et par application (téléphone,
télécopieur, terminal,
serveur informatique, etc.).
 Exemple: Exemple:
E1. Quelle
est la probabilité de saturation d'une hotline
(dont la durée de service suit une loi exponentielle et
la distribution des arrivées suit une loi de Poisson) sachant
que le trafic A de
la ligne est estimé à 2
Erlang (1 appel par heure pour 1 appel traité par ½ heure
- donc rapport de 2 sur 1) pour une seule ligne téléphonique
(N=1)
en utilisant le modèle d'Erlang-B?:
 (67.276)
(67.276)
E2. Dans une entreprise, on a dénombré aux heures
de pointe 200 appels d'une durée
moyenne de 6 minutes à l'heure (temps de service moyen).
Quelle est la probabilité
de saturation avec 20 opérateurs (sachant que la durée
de service suit une loi exponentielle et la distribution des arrivées
une loi de Poisson)?
La plus grosse difficulté ici est de calculer le trafic!
Il y a donc 200 appels par heure avec 10 appels traités
seulement par heure (puisque 6 minutes par appel dans une heure
de 60 minutes
font 10 appels). Le trafic A est donc de 200/10 soit 20
Erlang. En appliquant alors la relation précédente,
nous avons:
 (67.277)
(67.277)
Dans l'industrie, on admet un taux de saturation de 0.01%. En
jouant avec un tableur comme Microsoft Excel et l'outil Valeur
cible, nous trouvons rapidement que N doit alors être égal à 30.
PROBABILITÉ DE MISE EN ATTENTE M/M/k/∞ (FORMULE
D'ERLANG-C)
Considérons maintenant un système pour lequel les
appels
peuvent être mis en d'attente avant d'être servis lorsque les k
serveurs sont bloqués.
Il s'agit donc d'une file d'attente à capacité illimitée
de type M/M/k/∞ selon
la notation de Kendall.
Avec ce système, nous avons toujours:
 (67.278)
(67.278)
mais pour la probabilité de fin d'appel l'analyse devient plus
subtile. D'abord il y a la probabilité que les appels qui se trouvent
sur les canaux N disponibles cessent et qui est donnée
par:
 (67.279)
(67.279)
Mais dès que le nombre d'appels est plus grand que le nombre de
canaux de communication disponible, la probabilité que cessent
les appels est:
 (67.280)
(67.280)
Ce qui exprime que quel que soit le nombre d'appels, N ont
la probabilité d'être mis en attente dès que k (le
nombre d'appels) est supérieur ou égal à N.
Ainsi, pour résumer:
 (67.281)
(67.281)
En utilisant:
 (67.282)
(67.282)
Nous obtenons par décomposition du terme produit:
 (67.283)
(67.283)
D'où finalement:
 (67.284)
(67.284)
En utilisant l'expression de  : :
 (67.285)
(67.285)
Nous pouvons décomposer la sommation:
 (67.286)
(67.286)
et décomposer le deuxième produit:
 (67.287)
(67.287)
Sous l'hypothèse que:
 (67.288) (67.288)
La
somme:
 (67.289)
(67.289)
peut être simplifiée. Effectivement, en posant:
 (67.290)
(67.290)
il
vient:
 (67.291)
(67.291)
et comme nous l'avons montré lors de notre étude
de la fonction Zeta (cf. chapitre de Suites
Et Séries)
cette somme peut s'écrire sous la forme:
 (67.292)
(67.292)
Donc:
 (67.293)
(67.293)
Donc finalement:
 (67.294)
(67.294)
Puisque k représente le nombre d'appels, cette
dernière relation donne la probabilité d'avoir 0
appel (clients) pour un trafic permanent donné A dans
le système.
Nous avons donc pour  : :
 (67.295)
(67.295)
La probabilité cumulée de mise en file d'attente
se note C(N,
A). Elle est égale à:
 (67.296)
(67.296)
en procédant exactement comme dans les paragraphes précédents,
nous avons finalement:
 (67.297)
(67.297)
qui donne donc la probabilité de mise en
attente (et donc de saturation/blocage - c'est-à-dire que
tous les serveurs sont bloqués) dès
l'arrivée dans un système
disposant de N canaux à capacité infinie selon
le principe du premier arrivé/premier servi (FIFO: First
In/First Out) et pour un trafic A (exprimé donc en "Erlang")
et dans lequel les communications peuvent être mises en
attente (à l'opposé du modèle Erlang-B). Cette
dernière
relation est appelée "formule
d'Erlang-C". Traditionnellement on note:
 (67.298)
(67.298)
le "W" venant de l'anglais "Wait" (attendre).
Le modèle proposé ci-dessus est bien évidemment
critiquable, car en réalité la capacité de
la file d'attente est finie et certains clients abandonnent lorsque
l'attente
est trop longue.
 Exemple: Exemple:
Si nous prenons un taux d'arrivée de 1 appel par minute et une
durée moyenne de service de 5 minutes, nous avons alors:
 (67.299)
(67.299)
Si nous prenons un nombre N de 7 serveurs, nous avons:
 (67.300)
(67.300)
Donc 32.41% de probabilité cumulée d'être mis en attente. Ce
qui un peu beaucoup... (une règle empirique consiste à chercher
le nombre N de serveurs afin que cette dernière valeur descende
en dessous des 20%).
ASSURANCES
L'assurance est une opération pour laquelle une personne (l'assureur)
groupe en mutualité d'autres personnes (les assurés) afin de les
mettre en situation de s'indemniser mutuellement des pertes éventuelles
(les sinistres) auxquelles les expose la réalisation de certains
risques, au moyen des sommes (primes ou cotisations) versées par
chaque assuré à une masse commune gérée par l'assureur.
Le dénominateur commun de la majorité des lois définit le contrat
d'assurance comme un contrat en vertu duquel, moyennant le paiement
d'une prime fixe ou variable, une partie, l'assureur, s'engage
envers une autre partie, le preneur d'assurance, à fournir une
prestation stipulée dans le contrat au cas où surviendrait un événement
incertain que selon le cas, l'assuré ou le bénéficiaire, a intérêt à ne
pas voir se réaliser.
Évidemment, l'opération d'assurance a pour effet le transfert
(total ou partiel) des conséquences financières du risque subi
par l'assuré vers une société d'assurance. Dès lors, à la souscription
du contrat, l'assureur et l'assuré conviennent:
- D'un événement ou d'une liste d'événements, repris dans la
police d'assurance, et garantis par l'assureur.
- D'une prime payée par l'assuré à l'assureur.
Les dépenses prises en charge par l'assureur peuvent correspondre:
- Soit à des indemnités à verser à des tiers, au titre de la
responsabilité (civile, professionnelle ou autre) de l'assuré.
- Soit à la réparation des dommages subis par ce
dernier.
Les hypothèses d'usage de l'assurance sont les suivantes:
H1. D'un point de vue juridique, un contrat d'assurance est un "contrat
aléatoire" valide uniquement pour couvrir des
risques ayant une composante aléatoire.
H2. La "règle du jeu" du risque doit être stable
dans un laps de temps considéré comme long (au moins
quelques années).
H3. La perte maximale possible ne doit pas être trop importante
par rapport à la marge de solvabilité de l'assureur.
H4. La prime moyenne du risque doit être identifiable et quantifiable
selon des variables statistiques explicatives bien choisies afin éventuellement
de permettre une segmentation de la gestion des risques (petite
anecdote: lorsque les actuaires sont critiqués pour leurs pratiques
de ségmentation, nous entendons souvent la réponse: "nous ne faisons
pas de la discrimination, mais de la différenciation"...).
H5. Les risques doivent être indépendants (et s'ils sont
identiques distribués en termes de probabilités et
de pondération c'est mieux...)
et démontrables comme étant tels significativement
en utilisant les outils statistiques.
H6. Il doit exister un marché dans le sens que l'offre et la
demande d'assurance doivent arriver à un prix d'équilibre (en quelque
sorte l'équivalent de l'absence d'opportunité d'arbitrage en finance).
H7. L'espérance mathématique est considérée
comme le prix de la prime pure juste à faire payer aux assurés.
Définitions:
D1. La "prime pure" est
dans le domaine de l'assurance choisie comme étant l'espérance
mathématique de la charge; elle
correspond à la prime minimale que peut demander un assureur
pour ne pas, statistiquement, faire ruine de façon certaine.
D2. Le "chargement de sécurité" est
le montant qui vient s'ajouter à la prime pure et permettant à l'assureur
de pouvoir résister à la volatilité des remboursements.
D3. Le "chargement de frais de gestion" est
le montant qui vient s'ajouter aux deux précédents
et est lié au fonctionnement
de leur société, de la gestion des contrats, du recouvrement
des primes, du placement des actifs (prime technique de base),
des
taxes...
D4. Le "chargement de frais commerciaux" vient
s'ajouter aux trois précédents et est lié à l'acquisition
des contrats (commissions des intermédiaires,
frais des réseaux commerciaux, publicité).
D5. Au final, l'ensemble des coûts se retrouve dans la "prime
commerciale" qu'est celle communiquée au client.
Nous pouvons déjà en conclure que dans le cas d'un système d'assurance étatique
obligatoire ou facultatif, les frais de gestion et commerciaux
seront toujours inférieurs, sous l'hypothèse d'une méthode managériale égale, à un
système privé.
CALCUL DE PRIME
L'assureur ne connaît donc pas exactement le montant des sinistres
qui va survenir. En tarifant les contrats au niveau de la prime
pure (et en supposant une distribution des pertes symétriques),
l'assureur perd de l'argent une année sur deux. En l'absence de
fonds propres, cette situation conduirait immédiatement à la faillite.
Pour se protéger, l'assureur ajoute donc à sa prime un chargement
de sécurité. De nombreuses méthodes permettant de le déterminer
sont possibles, aucune n'ayant à ce jour supplanté largement les
autres:
- Chargement proportionnel à la prime pure. Le coefficient
de proportionnalité reflète l'idée que l'assureur
a de la volatilité du
risque.
- Chargement dépendant de l'écart-type des pertes.
Cette méthode
est une légère formalisation de la précédente.
Elle pose problème,
car elle introduira un chargement de sécurité qui
dépendra des
cas de gains (perte réelle inférieure à la
prime pure)
- Chargement dépendant d'un certain quantile des pertes
(par exemple le troisième quartile). Un tel chargement permet
de garantir que la prime sera suffisante dans un nombre de cas
déterminé à l'avance,
mais ne donne aucune information sur les cas de pertes techniques.
Considérons le cas où la population serait hétérogène, in extenso
deux classes  de
risque coexistent dans la population de poids respectifs de
risque coexistent dans la population de poids respectifs  avec
bien évidemment: avec
bien évidemment:
 (67.301)
(67.301)
Considérons une assurance maladie avec deux catégories
d'assurés
(jeunes en bonne santé A /seniors à risque B).
Pour simplifier l'exemple à l'extrême, imaginons que l'assureur
sait, à l'aide de ses statistiques internes, qu'un individu du
groupe A va coûter à l'assurance une somme définie par une
loi de distribution statistique que nous noterons dans le cadre
de ce chapitre:
 (67.302)
(67.302)
Soit à tout coût x est associée une certaine probabilité cumulée
donnée par la fonction  .
De même pour le groupe B: .
De même pour le groupe B:
 (67.303)
(67.303)
Si nous prenons alors au hasard un individu dans le portefeuille,
si  désigne
le groupe (notation traditionnelle en assurance), l'assureur devrait
donc réclamer en primes pures pour le groupe A: désigne
le groupe (notation traditionnelle en assurance), l'assureur devrait
donc réclamer en primes pures pour le groupe A:
 (67.304)
(67.304)
soit l'espérance de la fonction  . .
Idem pour le groupe B:
 (67.305)
(67.305)
Et pour un individu pris au hasard dans les deux groupes:
 (67.306)
(67.306)
Ce dernier cas étant appelé "mécanisme de solidarité".
Ainsi, les bons risques paient pour les mauvais risques...
La variance de la prime pure sera elle donnée par la relation
démontrée dans le chapitre de Statistiques lors de
l'étude des propriétés de la variance (variance de deux séries
statistiques):
 (67.307)
(67.307)
où nous voyons que le terme:
 (67.308)
(67.308)
au numérateur correspond à l'homogénéité des deux groupes. Et
donc que l'hétérogénéité fait accroître la variabilité de la prime
pure dans le mécanisme de solidarité.
Imaginons maintenant le cas où:
 (67.309)
(67.309)
et une assurance privée (1) qui pratique le mécanisme de solidarité et
une autre assurance (2) qui ne le pratique pas. Dans le cas présent,
nous devons distinguer deux situations d'un point de vue économique:
Si tous les assurés sont rationnels (sous-entendus un peu... égoïstes)
alors:
- Les jeunes en bonne santé représentant le groupe A vont
aller chez l'assurance privée (2) qui a segmenté les risques et
permet donc aux jeunes de payer moins cher.
- Les seniors en moins bonne santé représentant le groupe B vont
allez chez l'assurance privée (1) qui n'a pas segmenté les risques,
mais qui par idéologie a appliqué le principe de solidarité.
La conclusion est que l'assurance privée (1) va rapidement faire
faillite car:
- Les bons risques ne compensent plus le rabais de solidarité par égoïsme
- Nous sommes sur un marché concurrentiel où les assurances ne
sont pas idéologiques...
Ce constat s'appelle le "problème
d'anti-sélection" ou
de "sélection inverse" basée
sur l'approche G. Akerlof, prix Nobel d'Économie en
2001.
La conclusion est que la privatisation des assurances basées
sur un principe étatique (législation) de solidarité ne
peut pas fonctionner sans engendrer des coûts supplémentaires
aux primes pures à cause d'une anti-sélection périodique
qui engendre un flux constant d'assurés d'une assurance à une
autre et donc engendre des coûts administratifs et informatiques
phénoménaux! Donc en
tout point la suppression de la concurrence reste meilleure en
terme de solidarité mais par contre pas en termes d'emplois
pour les salariés des assurances (qui se trouveraient alors
en grande majorité au chômage...).
Ainsi, la suppression de la concurrence pour des services d'assurances
qui ont toutes des prestations de qualité équivalentes
(comme c'est le cas pour l'assurance maladie en Suisse par exemple...) élimine
le principe d'anti-sélection, applique de manière
concrète le mécanisme
de solidarité voulu par l'état et enfin diminue les
coûts administratifs
dus aux va-et-vient des assurés et des développements
d'outils informatiques de gestion maison coûtant des millions à chaque
assurance et qui engendrent des coûts qui au final sont répercutés
sur le prix de la prime commerciale!
À ceci, il faut rajouter que pour diminuer la volatilité globale
(écart-type global), une assurance devrait en théorie
segmenter les risques à l'infini ce qui en fait un système
non viable pour certains domaines particuliers de l'assurance.
Mais il faut se rappeler que cette conclusion n'est valable que
si les prestations des assurances sont identiques (ou quasi similaires)
sur un marché donné!
Signalons également un souci récurrent dans le domaine des assurances,
appelé "aléa moral", qui se base sur le constat que les
personnes qui s'assurent ont tendance à être moins prudentes que
les personnes qui ne s'assurent pas. En d'autres termes, l'assurance
génère du risque.
PRISE EN COMPTE DE L'EXPERIENCE
Pour l'instant, pour déterminer une prime d'assurance, nous avons
noté qu'il était possible d'intégrer des variables exogènes (sexe, âge,
enfants, puissance du véhicule, nationalité, environnement, etc.).
Mais un point important à ne pas négliger est le
retour d'expérience des sinistres d'un assuré. Voyons
en un exemple concret.
Supposons que le nombre de sinistres sur un an,
pour un assuré donné,
suive une loi de Poisson (loi des événements rares)
donnée pour
rappel par (cf. chapitre de Statistiques):
 (67.310)
(67.310)
ce qui se note dans le domaine des assurances:
 (67.311)
(67.311)
Supposons que la population des assurés est séparée en
trois classes de risques suivant chacune une distribution de Poisson
telle que:
 (67.312)
(67.312)
En d'autres termes, il y a 70% de la population totale qui suit
une loi de Poisson d'espérance 1 (classe de bons risques),
20% qui suit une loi de Poissons d'espérance 2 (classe de
risques moyens), et 10% qui suit une loi de Poisson d'espérance
3 (classe de mauvais risques).
Évidemment l'espérance globale d'un individu du
portefeuille est alors de l'espérance de la "distribution
mixte":
 (67.313)
(67.313)
Supposons que les coûts d'un incident soient fixes et de type
indemnitaires de 1'000.-. Nous pouvons alors nous demander quelle
devrait être la prime pour un assuré, sachant que la première année,
il a eu 2 sinistres. Ce qui revient à se demander, quel est le
nombre d'accidents qu'il risque d'avoir la deuxième année.
Si nous notons  le
nombre d'accidents de la première année, et le
nombre d'accidents de la première année, et  le
nombre d'accidents a posteriori connaissant le
nombre d'accidents a posteriori connaissant  nous
nous retrouvons donc avec un problème de probabilité conditionnelle
(une démarche bayésienne autrement dit...) conforme à ce
que nous avons étudié dans le chapitre de Probabilités: nous
nous retrouvons donc avec un problème de probabilité conditionnelle
(une démarche bayésienne autrement dit...) conforme à ce
que nous avons étudié dans le chapitre de Probabilités:
 (67.314)
(67.314)
où nous avons adopté conformément à la
tradition dans le domaine la notion de "|" pour signaler
la probabilité conditionnelle.
Mais nous ne pouvons pas calculer le numérateur, car nous
ne savons pas à l'avance quelle sera la valeur de  .
Nous allons donc calculer l'espérance conditionnelle espérée
afin de contourner ce problème: .
Nous allons donc calculer l'espérance conditionnelle espérée
afin de contourner ce problème:
 (67.315)
(67.315)
Nous avons d'abord:
 (67.316)
(67.316)
Ce dernier calcul (espérance de la distribution mixte) étant
noté dans
le domaine de l'assurance de la manière suivante:
 (67.317)
(67.317)
Si nous considérons les deux variables aléatoires comme indépendantes:
 (67.318)
(67.318)
Il vient alors immédiatement que:
 (67.319)
(67.319)
Nous retombons donc sur une valeur connue correspondant à la
prime pure:
 (67.320)
(67.320)
identique au calcul de:
 (67.321)
(67.321)
Donc les variables aléatoires  sont
confondues avec celle de la classe de risque! sont
confondues avec celle de la classe de risque!
Ce système n'est alors bien évidemment pas conforme au bonus-malus.
Nous devons alors considérer que les deux variables aléatoires
ne sont pas indépendantes (au fait c'est la définition même du
bonus-malus!).
Ainsi, si les deux variables aléatoires ne sont pas indépendantes,
nous avons:
 (67.322)
(67.322)
Et alors:
 (67.323)
(67.323)
À comparer avec la prime pure sans bonus-malus de 1.4!
Ce qui est délicat avec cette méthode, c'est que
lorsque l'on cumule les années... cette
approche bayésienne devient pénible.
Effectivement, imaginons que nous souhaiterions déterminer
la prime pure de la troisième année sachant que la
deuxième année, l'assuré a
eu 1 accident. Nous avons alors l'espérance conditionnelle:
 (67.324)
(67.324)
que nous laissons le soin au lecteur de développer...
Nous remarquons de ce qui a été vu ci-dessus que l'espérance d'une
distribution mixte définie par:
 (67.325)
(67.325)
est donc trivialement:
 (67.326)
(67.326)
FACTEUR D'ACTUALISATION D'UNE ASSURANCE RETRAITE
Recherchons maintenant quelque chose qui n'a absolument rien à
voir avec ce que nous venons de calculer et qui est le "facteur
d'actualisation" par
lequel nous devons diviser un solde d'épargne au début de la retraite,
pour
répartir ce montant sur chaque année durant la retraite, selon l'espérance de
vie ainsi que les taux d'intérêt et d'inflation. L'approche ici sera donc de
simplifier en se questionnant sur quel niveau d'épargne il sera nécessaire
d'avoir accumulé au début de la retraite pour obtenir une rente
de 1.- (réelle) chaque année durant la retraite. C'est à partir de ce niveau d'épargne nécessaire pour
recevoir 1.- qu'il sera possible d'utiliser n'importe quel solde d'épargne pour
dériver quelle rente sera disponible à l'épargnant.
En premier lieu, nous allons définir les paramètres utilisés:
- m Nombre
de périodes à la retraite (années ou mois)
-  Solde
d'épargne à la période k Solde
d'épargne à la période k
- p Prestation périodique (que nous supposerons ici annuelle)
- i Taux périodique d'inflation (supposé ici constant et annuel)
- R Taux de rendement moyen géométrique du marché (supposé constant
et annuel)
-  Facteur
d'actualisation à l'âge m Facteur
d'actualisation à l'âge m
Ainsi, comme mentionné plus haut, nous sommes à la recherche
du niveau d'épargne initial,  ,
qui permettra d'obtenir une prestation périodiques (donc annuelle
dans le cas présent), p, égale à 1.-
indexée sur
l'inflation i. ,
qui permettra d'obtenir une prestation périodiques (donc annuelle
dans le cas présent), p, égale à 1.-
indexée sur
l'inflation i.
En commençant à partir du solde initial  ,
en présumant que les prestations sont versées au début de l'année
(praenumerando), nous pouvons dériver le solde restant à la fin
de la première
période de retraite ainsi: ,
en présumant que les prestations sont versées au début de l'année
(praenumerando), nous pouvons dériver le solde restant à la fin
de la première
période de retraite ainsi:
 (67.327)
(67.327)
Plus précisément, le retraité aura encaissé un montant p pour
la première période, laissant le résiduel être exposé au rendement
moyen géométrique du marché R.
Ensuite, d'une manière similaire
et en considérant que les prestations sont indexées sur l'inflation i,
nous pouvons calculer ce solde en fin de deuxième période
et de toute période k subséquente:
 (67.328)
(67.328)
ou:
 (67.329)
(67.329)
ou encore:
 (67.330)
(67.330)
et ainsi de suite... Il vient alors:
 (67.331)
(67.331)
ou autrement écrit:
 (67.332) (67.332)
Ainsi nous avons, à un terme près, une série
géométrique de raison q connue dans le dernier terme.
Nous avons effectivement démontré dans le chapitre
de Suites Et Séries que pour j allant de 0 à n celle-ci
vaut :
 (67.333) (67.333)
et donc:
 (67.334) (67.334)
Il nous est donc possible de réécrire, pour la dernière période
de retraite m, le solde de la manière suivante:
 (67.335) (67.335)
Remarquons que dans le cas peu probable et particulier où le
rendement moyen géométrique du marché est égal à l'inflation, c'est-à-dire
si  ,
nous avons: ,
nous avons:
 (67.336) (67.336)
À ce stade, la raison pour laquelle le terme  est
un paramètre important est qu'il s'agit du solde du retraité à la
fin de sa période de retraite, c'est-à-dire au décès (mort). Il
sera ici présumé que le retraité ne planifie pas de legs et donc
que est
un paramètre important est qu'il s'agit du solde du retraité à la
fin de sa période de retraite, c'est-à-dire au décès (mort). Il
sera ici présumé que le retraité ne planifie pas de legs et donc
que
 (67.337)
(67.337)
Conséquemment, pour  ,
cela revient à trouver S pour lequel: ,
cela revient à trouver S pour lequel:
 (67.338)
(67.338)
Nous pouvons alors établir dans ce cas que pour  : :
 (67.339)
(67.339)
Et dans
le cas peu probable et particulier où le rendement moyen géométrique
du marché est égal à l'inflation, c'est-à-dire si  ,
nous avons: ,
nous avons:
 (67.340)
(67.340)
et nous déduisons un résultat logique:
 (67.341)
(67.341)
Pour la suite, revenons au cas réaliste où  et
donc avec: et
donc avec:
 (67.342)
(67.342)
et notons:
 (67.343)
(67.343)
La relation antéprécédente s'écrit alors sous une forme un peu
plus condensée:
 (67.344)
(67.344)
où:
 (67.345)
(67.345)
est donc le facteur d'actualisation. De plus, nous avons la relation
suivante donnant l'espérance d'être en vie à l'age a (âge
correspondant à l'âge supposé de décès dans le cas présent) démontrée
dans le chapitre de Dynamique Des Populations:
 (67.346)
(67.346)
avec pour rappel la fonction e(a,s) représentant
l'espérance
de vie conditionnelle à l'âge a et pour le sexe s.
ASSURANCES DE RENTES
Nous allons maintenant étudier une rente qui n'est pas
versée d'une manière certaine mais d'une manière "viagère",
c'est-à-dire qui dépend de la survie de l'assuré.
Il va donc falloir c'est multiplier chaque terme de rente par la
probabilité qu'il lui soit versé.
Évidemment, dans la majorité des cas, ce qui va
nous intéresser sera la "valeur actuelle" des
rentes viagères afin de savoir ce que devra payer l'assureur
(et donc ce qu'il devra avoir capitalisé). Il existe deux
types de rentes viagères courantes. Nous allons voir en
quoi consiste chacune. Mais avant cela, rappelons que nous avons
vu dans le chapitre de Dynamique Des Populations que la probabilité d'être
en vie à une x + 1 sachant qu'on est en vie à un age
x est donné par:
 (67.347)
(67.347)
et rappelons (suite à la demande d'un lecteur)
que la valeur actuelle d'un capital  à taux
constant payable dans 1 année est donné par (cf.
chapitre d'Économie): à taux
constant payable dans 1 année est donné par (cf.
chapitre d'Économie):
 (67.348)
(67.348)
Ce qui donne donc la somme à placer à un
taux t% pour avoir après un an le capital  . . En
combinant probabilité de survie et valeur actuelle, nous
pouvons définir dans le cas d'une rente la prime unique
de la prestation comme étant:
 (67.349)
(67.349)
Si l'assuré est en vie à l'échéance,
c'est l'assuré qui gagne au jeu (en réalité ils gagnent
très souvent les deux...), dans le cas contraire c'est l'assureur (qui
alors lui dans ce cas là est vraiment très gagnant!).
Bien évidement dans le cas ci-dessus, extrêmement
simplifié, il n'y a qu'un seul versement de la part de l'assureur.
Mais dans la réalité il peut y en avoir plusieurs
(c'est ce que nous allons étudier), le versement de l'assuré peut
ne pas être sous la forme d'une prime unique, le taux moyen
géométrique du marché peut ne pas être
constant (ce dernier cas étant traité normalement
avec des simulations de Monte-Carlo).
Donc même si ce que nous allons voir est très simplifié par
rapport à ce qui se fait dans les assurances par les actuaires,
cela donne déjà une piste de recherche pour des modèles
plus élaborés.
RENTE VIAGÈRE TEMPORAIRE
La rente viagère temporaire consiste pour l'assureur à verser
des termes de rentes, tant que l'assuré est en vie mais
au maximum durant n années après qu'il ait atteint
un âge x donné mais tout de suite après que
l'assuré ait payé sa prime unique (qui correspond
justement à l'âge x en question). L'objectif est donc
de déterminer le capital (valeur actuelle) que doit avoir
amassé l'assureur au moment du commencement du paiement
de ces rentes (ce capital pouvant aussi être demandé sous
forme de paiements multiples plutôt que sous la forme d'une
prime unique).
Évidemment ce cas est peu réaliste car peu de personnes
vont payer une prime unique (grosse somme d'argent) à un
moment x de leur vie pour commencer tout de suite à recevoir
des rentes. Mais c'est pédagogiquement intéressant
avant d'aborder le type de rente viagère différée
et qui est un peu plus réaliste.
La rente viagère temporaire praenumerando (in extenso:
la valeur actuelle de la rente viagère unitaire payable
praenumerando tant que l'assuré est en vie mais au maximum
pendant n années) est donnée par la relation suivante
qui découle des développements effectués dans
le chapitre d'Économie à la différence que
l'on y trouve des coefficients de probabilité de survie:
 (67.350)
(67.350)
où pour rappel (cf.
chapitre d'Économie),
nous avons le facteur d'escompte (dans le cas présent nous
devrions plutôt utiliser le terme de "facteur de capitalisation")
qui est:
 (67.351)
(67.351)
En toute généralité, le terme
(cf. chapitre de Dynamiques Des Populations):
 (67.352)
(67.352)
est appelé "valeur
probable du capital différé".
La rente viagère
temporaire postnumerando (valeur actuelle d'une rente viagère
unitaire payable postnumerando tant que l'assuré est en
vie mais au maximum pendant n années)
est elle donnée par:
 (67.353)
(67.353)
 Exemple: Exemple:
Nous souhaitons verser une rente de 1'000.- durant 3 ans à un
homme de 40 ans. La prime unique qu'il devra payer si ni l'intérêt,
ni la mortalité n'interviennent dans les calculs, ensuite
si seulement l'intérêt est considéré dans
les calculs et enfin en prenant en compte l'intérêt
et la mortalité est donnée respectivement par les
trois relations suivantes:
 (67.354)
(67.354)
RENTE VIAGÈRE DIFFERÉE
Les rentes viagères différées constituent
la majorité des contrats d'assurance de rentes. L'assuré s'acquitte
toujours d'une prime unique, pour recevoir une rente s'il est en
vie à un certain âge (à l'âge de sa retraite
par exemple), donc commencer à recevoir la rente k années
après avoir payé la prime unique, mais cette fois-ci
jusqu'à son décès.
La rente viagère différée praenumerando (valeur
actuelle d'une rente viagère unitaire différée
de k années et payable praenumerando jusqu'à décès
de l'assuré) est donnée par:
 (67.355)
(67.355)
où  est
la dernière valeur (numéro
de ligne) de la table de mortalité. Le lecteur remarquera
peut-être que si nous posons k = 1 (sans différé)
et est
la dernière valeur (numéro
de ligne) de la table de mortalité. Le lecteur remarquera
peut-être que si nous posons k = 1 (sans différé)
et  , nous retombons sur une rente viagère temporaire postnumerando , nous retombons sur une rente viagère temporaire postnumerando
 . .
Donc normalement pour un même âge x et
une même durée de rente supposée, la valeur
actuelle de la rente viagère différée (prime
unique) est inférieur à celle de rente viagère
temporaire et ce d'autant plus petit que le différé est
grand.
La rente viagère différée postnumerando (valeur
actuelle d'une rentre viagère unitaire différée
de k années et payable postnumerando jusqu'à décès
de l'assuré) est donnée par:
 (67.356)
(67.356)
Évidemment, les deux rentes ci-dessus ont
la même fin car étant donné que c'est jusqu'à la
mort, c'est difficile de payer en postnumerando de la mort...
Signalons encore qu'il est possible mathématiquement de
créer
une rente temporaire ET différée mais c'est rare
et donc nous n'en ferons pas l'étude ici.
Remarque: Contrairement aux rentes certaines, il n'existe pas
ici de formule simplifiée permettant un calcul rapide de
ces rentes basées sur les tables de mortalité. L'utilisation
d'un tableur ou la programmation de ces fonctions permet de calculer
facilement les valeurs actuelles des prestations viagères. À l'époque
où l'informatique n'avait pas cours, on construisait des
tables appelées "nombre de commutations" qui permettaient
d'obtenir les informations voulues.

- Gestion de la production,
V. Giard, Éditions
Economica (2ème édition), ISBN10: 2717815279 (1068 pages) - Imprimé en
1988
- Statistiques descriptives pour
les gestionnaires,
V. Giard, Éditions Economica, ISBN10: 2717828893 (111 pages) - Imprimé en
1995
- Queueing Modelling Fundamentals (2ème édition), Éditions
John Wiley & Sons, Ng Chee-Hock + Soong Boon-Hee, ISBN13:
9780470519578 (294 pages) - Imprimé en
2008
|