News :: Erreur :: Visiteurs :: ClearType :: Imprimer ::

TRIGONOMÉTRIE | GÉOMÉTRIE EUCLIDIENNE | GÉOMÉTRIES NON-EUCLIDIENNES
GÉOMÉTRIE PROJECTIVE | GÉOMÉTRIE ANALYTIQUE | GÉOMETRIE DIFFÉRENTIELLE
FORMES GÉOMÉTRIQUES | THÉORIE DES GRAPHES

Dernière mise à jour de ce chapitre: 2017-12-31 17:58:44 | {oUUID 1.781}
Version: 3.0 Révision 8 | Avancement: ~80%
vues depuis le 2012-01-01: 12'752

LISTE DES SUJETS TRAITÉS SUR CETTE PAGE

Comme nous l'avons déjà mentionné dans le chapitre de Géométrie Non-Euclidienne, la géométrie différentielle est la branche de la géométrie qui vise à étudier les propriétés locales (au voisinage d'un point) et intrinsèques des courbes et des surfaces non-euclidiennes (comme une généralisation des surfaces euclidiennes!).

La géométrie différentielle tient son nom au fait qu'elle est née de la possibilité d'une interprétation cinématique que le calcul infinitésimal apporte à l'étude des courbes. Les points que nous aborderons ici serviront aussi bien dans l'étude de la mécanique classique que de l'analyse complexe appliquée à de nombreux domaines de l'étude des champs.

COURBES PARAMÉTRÉES

Définition: Nous assimilerons "l'espace physique" à  et le supposerons muni d'un repère  et nous noterons B la base

Soient un ensemble  et une fonction  telle que:

  (25.1)

Choisissons  et posons  que nous noterons par abus de langage  nous pouvons alors énoncer la définition suivante: le couple (f , I) où f est une fonction continue est appelé "arc paramétré".  est appelée le "support" de (f , I) et  est une "origine" de (f , I).

Avant de continuer, rappelons qu'en géométrie différentielle, "l'abscisse curviligne" est une sorte de variante algébrique de la longueur d'un arc (c'est donc l'analogue, sur une courbe, de l'abscisse sur une droite orientée).

Considérons maintenant l'abscisse curviligne (cf. chapitre de Calcul Tensoriel):

  (25.2)

nous savons que dans un espace euclidien canonique (dans ) l'abscisse curviligne s'écrit alors:

  (25.3)

avec  et comme nous avons , il reste:

  (25.4)

Dans le système cartésien:

  (25.5)

il vient donc que:

  (25.6)

qui est donc l'élément différentiel linéaire d'un espace euclidien (le plus court chemin ou encore la "géodésique" ou encore " l'abscisse curviligne différentielle") que nous avons déjà rencontré à maintes reprises dans différents chapitres du site. Ce n'est donc rien de nouveau ni de surprenant!

Si nous nous restreignons au plan, l'abscisse curviligne différentielle d'une courbe plane s'écrit alors:

  (25.7)

Nous savons déjà comment utiliser cette dernière équation (nous en avons fait usage dans le chapitre de Mécanique Analytique). Mais comme un rappel n'est jamais mauvais, faisons des exemples avec une droite, une parabole et un demi-cercle (le choix n'est pas innocent...).

Exemples:

E1. Considérons l'équation générale d'une droite dans le plan (ce n'est pas une courbe plane pour rappel mais une droite plane):

  (25.8)

Il vient alors immédiatement:

  (25.9)

Dès lors:

  (25.10)

E2. Considérons l'équation générale d'une parabole dans le plan:

  (25.11)

Il vient alors immédiatement:

  (25.12)

Dès lors:

  (25.13)

E3. Considérons le réarrangement de l'équation générale d'un cercle de rayon R dans le plan (cf. chapitre de Géométrie Analytique):

  (25.14)

Il vient alors immédiatement:

  (25.15)

Dès lors:

  (25.16)

Remarquons qu'en faisant une approximation de Maclaurin (lorsque x vaut donc zéro, ce qui correspond à l'étude du pôle du cercle), nous avons (cf. chapitre de Suites Et Séries):

  (25.17)

Suite à la demande d'un lecteur voici les détails du développement du résultat précédent. Rappelons d'abord la série de Taylor (cf. chapitre Suites Et Séries):

  (25.18)

Si nous posons , nous obtenons la série de Maclaurin:

  (25.19)

Donc il vient en procédant en deux étapes:

  (25.20)

En prenant :

  (25.21)

Il vient alors immédiatement:

  (25.22)

Dès lors:

  (25.23)

Nous voyons alors que l'abscisse curviligne du cercle dans le plan devient celle d'une parabole lorsque nous faisons un développement en série de Maclaurin de l'équation du cercle au pôle.

Nous pourrions faire de même avec une hyperbole ou une ellipse et nous retrouver avec la même forme d'abscisse curviligne différentielle, généralement notée par tradition:

  (25.24)

où k_x est appelé "paramètre de la parabole osculatrice".

Ces exemples étant clos, continuons un peu avec la théorie. Nous pouvons bien évidemment réécrire notre abscisse curviligne différentielle en divisant par dt des deux côtés de l'égalité tel que:

  (25.25)

Exemple:

Voyons une application de l'abscisse curviligne différentielle paramétrée avec une hélice (les exemples sont jolis en géométrie différentielle et valent donc la peine d'être vus...) qui est un exemple typique de courbe gauche:

Soient  et la fonction:

  (25.26)  

avec  et les coordonnées paramétriques:

  (25.27)

Nous avons alors avec Maple 4.00b en prenant r et h comme étant égaux à l'unité:

>with(plots):
>spacecurve([cos(t),sin(t),t,t=-4*Pi..4*Pi,numpoints=1000]);

Figure: 25.1 - Représentation paramétrique d'une hélice avec Maple 4.00b

La fonction f est un arc paramétré dont le support est appelé une "hélice", r en est le rayon et h le pas. En prenant  comme origine, l'abscisse curviligne de cette hélice (un morceau) est donnée par:

  (25.28)

Donc:

    (25.29)

et alors:

  (25.30)

ISOCLINES

Voyons maintenant un point très important en mathématiques mais en plus dans l'ingénierie médicale, astrophysique, météorologie (parmi encore beaucoup d'autres domaines) que sont les isoclines.

Avant d'aborder le sujet sous forme mathématique, nous proposons au lecteur d'ouvrir Matlab 5.0.0.473 (nous avons déjà fait à peu près le même exemple avec Maple 4.00b dans le chapitre d'Analyse Fonctionnelle) et d'y écrire:

EDU» [xx,yy,z]=peaks;
EDU» figure(1);mesh(xx,yy,z);title('peaks')

Figure: 25.2 - Tracé initial dans Matlab 5.0.0.473

ensuite pour des raisons esthétiques, d'écrire:

EDU» figure(2);surf(xx,yy,z);title('surf')

Figure: 25.3 - Amélioration du gradient de couleurs dans Matlab 5.0.0.473

Ensuite nous aimerions que Matlab nous trace quelques courbes de niveau (les points où la valeur de la fonction f(x,y) est constante), appelées par les matheux des "isoclines" ou "courbes d'iso-niveau". Il faut alors écrire:

EDU» figure(3);contour3(xx,yy,z);title('contour')

Figure: 17.4 - Affichage des isoclines de la fonction dans Matlab 5.0.0.473

Nous allons ensuite lui demander de les projeter sur le plan X,Y.

Ce qui donne:

EDU» figure(3);contour(xx,yy,z);title('contour')

Figure: 25.5 - Projection des isoclines sur un plan dans Matlab 5.0.0.473

Et ce sont ces courbes qui vont nous intéresser. Nous souhaiterions déterminer les équations dans le plan de celles-ci sous forme explicite. Mais avant cela amusons-nous avec Matlab en écrivant encore:

EDU» figure(4);pcolor(xx,yy,z);title('gradient')

Figure: 25.6 - Représentation plane des isoclines avec gradients colorés dans Matlab 5.0.0.473

mais nous pouvons faire encore mieux en enlevant la grille avec la commande:

EDU» shading interp

Figure: 25.7 - En retirant la grille...

Ensuite, sans fermer le graphique ci-dessus créé par Matlab 5.0.0.473 rajoutez maintenant la ligne:

EDU» hold on
EDU» contour(xx,yy,z,'k')

Figure: 25.8 - Association isoclines projetées avec gradients de couleurs

Considérons pour déterminer l'équation des isoclines la fonction  de  et que nous imposerons -différentiable.

La relation:

  (25.31)

définit une courbe  plane appelée "isocline". C'est une courbe telle que, lorsque x varie, y ne varie donc pas n'importe comment mais précisément de telle sorte que f reste constante.

Nous avons vu dans le chapitre de Calcul Différentiel Et Intégral que la différentielle de f, pour des variations infinitésimales quelconques de x et y, est:

  (25.32)

Maintenant, si nous voulons que quand x varie de dx, la valeur de la fonction f ne change pas, il faut que dy ne soit pas n'importe quoi mais tel que la variation df soit nulle. Autrement dit:

  (25.33)

le long de . Mais cette équation ne sert à rien en tant que telle, mais elle nous fixe le rapport de la dérivée de l'isocline dans le plan tel que:

  (25.34)

ce qui nous donne la pente de la tangente à  et donc après par intégration, la fonction recherchée elle-même!

Il va de soi que le vecteur tangent à la courbe  est donc un vecteur parallèle à celui ayant pour composantes (par correspondance avec la relation précédente):

  (25.35)

que nous noterons:

  (25.36)

De plus rappelons que le gradient est donné par (cf. chapitre de Calcul Vectoriel):

  (25.37)

Nous remarquerons que ces deux derniers vecteurs sont perpendiculaires (résultat qui nous sera utile dans le chapitre d'Analyse Complexe). Effectivement:

  (25.38)

En d'autres termes, le vecteur  définit les lignes orthogonales à la courbe  .

Exemple:

Prenons l'équation d'une parabole particulière dans :

  (25.39)

Nous avons donc les isoclines qui sont données par:

  (25.40)

d'où leur équation dans le plan:

  (25.41)

Soient des cercles dans le plan dont le rayon est égal à la racine carrée de la constante choisie correspondante à la hauteur z de la fonction f !

Calculons maintenant la pente de la tangente à :

  (25.42)

ce qui est conforme à la simple dérivée de:

  (25.43)

Nous avons aussi:

  (25.44)

Nous voyons qu'en  ce vecteur est vaut:

  (25.45)

ce qui est bien conforme au vecteur tangent que nous avons au cercle en ce point de l'axe des abscisses.

TRIEDRE DE FRENET

Le repère de Frenet est un outil d'étude du comportement local des courbes. Plus exactement, il s'agit d'un repère local associé à un point décrivant une courbe . Son mode de construction est différent selon que l'espace ambiant est de dimension 2 (courbe plane) ou 3 (courbe gauche).

Le repère de Frenet, et les formules de Frenet (donnant les dérivées des vecteurs de ce repère), permettent de mener de façon systématique des calculs de courbure, de torsion pour les courbes gauches et d'introduire des concepts géométriques intéressants associés aux courbes.

Considérons pour commencer une courbe avec son abscisse curviligne s(t) et  son origine. Nous notons par définition:

  (25.46)

la tangente à la courbe  de paramètre t au voisinage d'un point M par rapport à un repère posé en O avec ds qui se calcule comme nous l'avons montré précédemment.

Il est intéressant de remarquer que si t s'interprète comme le temps, alors nous avons une vitesse:

  (25.47)

et donc le vecteur est dirigé dans le sens du mouvement.

De plus, par construction et définition de l'abscisse curviligne, nous avons toujours:

  (25.48)

et donc le vecteur tangent au point M est unitaire (et non nul!).

Maintenant, sans savoir exactement à quoi cela va nous servir pour l'instant, intéressons-nous au vecteur:

  (25.49)

Sachant trivialement de ce qui précède que:

  (25.50)

Alors, nous avons:

  (25.51)

donc déjà n'est a priori pas unitaire et lui est perpendiculaire (résultat qui va nous servir plusieurs fois par la suite donc il faudra s'en souvenir)!

Posons maintenant:

  (25.52)

Étant donné le résultat précédent,  est le vecteur perpendiculaire, appelé "vecteur de courbure" unitaire, à  en M (nous disons que ce couple de vecteur est "orthonormal direct") et C est par définition la "courbure".

Nous pouvons également aborder la courbure C d'une façon plus géométrique plutôt que par une définition tombée du ciel:

Nous savons à ce point de notre discours qu'en un point  d'une courbe (dérivable au moins une fois en tout point...), il existe un vecteur tangent non nul qui est .

En tout point voisin M (d'abscisse curviligne s), le vecteur tangent peut s'écrire en approximation:

  (25.53)

si la courbe se trouve localement dans un même plan (car nous étudions ici la courbure et non la torsion de la courbe)!

Deux normales en M et M₀ se coupant donc en un point Ω, la figure suivante:

Figure: 25.9 - Décomposition du vecteur tangent de la trajectoire courbe

montre qu'au premier ordre en ds, le point M peut être considéré localement comme déduit du point M₀ par une rotation de centre Ω.

Le cercle ainsi défini, de rayon:

  (25.54)

est celui qui tangente le mieux la courbe localement au point M₀. Son rayon se déduit de la figure (deux triangles semblables à la limite):

  (25.55)

d'où, puisque  est unitaire, la définition et la valeur de la courbure:

  (25.56)

et voilà!

Il est possible d'interpréter le concept de courbure comme la vitesse de rotation de la base de Frenet par rapport à une direction fixe.

Le couple de vecteurs (, ) est appelé "repère de Frenet" et ses vecteurs de base les "vecteurs de Frenet".

Le repère de Frenet est un repère mobile puisque les éléments de ce repère changent selon le point considéré. En physique, il ne faut pas confondre cette notion avec celle de référentiel: puisque les vecteurs de Frenet se déplacent avec le point!

Si , alors comme vu précédemment:

  (25.57)

où R est appelé le "rayon de courbure".

Quant à la relation:

  (25.58)

elle est appelée "1ère formule de Frenet" et montre que et sont colinéaires et donc leur produit vectoriel est nul (résultat utilisé plus loin).

Ces relations se justifient par l'analogie avec la mécanique. Effectivement, nous avons démontré plus haut que:

  (25.59)

Calculons maintenant l'accélération:

  (25.60)

nous retrouvons alors le résultat obtenu dans le chapitre de Mécanique Classique lors de notre étude du plan osculateur.

Pour donner une interprétation géométrique plus exacte de la courbure, nous définissons d'abord par  le centre du "cercle osculateur" (se trouvant dans le plan osculateur) ou "cercle de courbure" de rayon R qui tangente le mieux  localement  tel que dans le repère de Frenet:

  (25.61)

Pour préciser géométriquement ce qu'est le cercle osculateur, prenez une courbe, et un point M sur cette courbe. Tracez ensuite la normale au point de cette courbe localement plane et prenez un point sur la normale. Alors, le cercle de centre O passant par le point M est tangent à la courbe. Mais tous les cercles tangents à la courbe ne sont pas tangents de la même façon! En effet, si est loin de M, le cercle va se situer plutôt à l'extérieur de la courbe (cercle bleu dans la figure ci-dessous). Si est proche de M, le cercle va se situer plutôt à l'intérieur de la courbe (cercle rose dans la figure ci-dessous). Le rayon limite entre être "à l'intérieur de la courbe" et être "à l'extérieur de la courbe" est par convention le "rayon de courbure" que nous avons défini plus haut. Le cercle correspondant à ce rayon est alors le fameux "cercle osculateur".

Figure: 25.10 - Représentation du cercle osculateur

Dans le cas particulier où  est un vecteur constant:

  (25.62)

et donc  ce qui implique que R n'est plus défini. Nous disons quelquefois dans ce cas que le rayon de courbure de  est infini (une droite présente alors une courbure nulle en tout point).

Étudions maintenant le vecteur perpendiculaire au plan osculateur défini par:

  (25.63)

Nous pouvons déjà dire, étant donné que  et  sont unitaires que  l'est aussi (ce qui va nous servir plus loin)!

Démontrons que  est orthogonal à :

  (25.64)

où nous avons pris le cas particulier (mais de toute manière en généralité et sont colinéaires comme nous l'avons démontré donc le produit vectoriel entre ces deux vecteurs est toujours nul).

C.Q.F.D.

Démontrons maintenant que   est colinéaire à :

De la même manière que nous avons démontré plus haut que est perpendiculaire à , nous démontrons que est perpendiculaire à !

Nous avons donc:

  (25.65)

Et étant donné que est aussi perpendiculaire à (démonstration précédente) il est donc colinéaire à .

C.Q.F.D.

Posons maintenant:

  (25.66)

Cette relation constitue la "2^ème formule de Frenet" où par définition,  est le "vecteur binormal" de  au point M et  en est la "torsion" et R' le "rayon de torsion".

Nous pouvons maintenant établir la "3^ème formule de Frenet":

  (25.67)

d'où nous tirons:

  (25.68)

Or de par les propriétés du produit vectoriel:

  (25.69)

d'où la 3^ème formule de Frenet:

  (25.70)

Nous appelons "trièdre de Frenet" associé à  au point M, le repère naturel orthonormal de l'espace :

Figure: 25.11 - Représentation du trièdre de Frenet

où, en mécanique, le vecteur est colinéaire à la vitesse et l'accélération tangentielle et est colinéaire à l'accélération normale.

Exemple:

E1. Cherchons le rayon et le centre de courbure en tout M à notre hélice définie plus haut comme exemple pratique. Rappelons que sa fonction paramétrique est donnée par:

  (25.71)

et que:

  (25.72)

Nous avons dès lors:

  (25.73)

Au passage, vous remarquerez que nous avons bien:

  (25.74)

Ainsi, la courbure (l'inverse du rayon de courbure) est donnée par:

  (25.75)

Donc, le rayon de courbure vaut:

  (25.76)

Ce qui est conforme à l'intuition puisque, lorsque le pas h de l'hélice est nul, le rayon de courbure vaut r et lorsque le pas h tend vers l'infini le rayon de courbure tend vers l'infini aussi et la courbure vers zéro. Cet exemple est un cas fameux d'ingénierie appliquée aux cheminées d'évacuation de fumées qui sont entourées d'une hélice d'Archimède et dont l'objectif est de faire monter les flux d'air vers le haut (la difficulté étant de déterminer le rayon R de la plaque de métal à couper qui suivra le mieux la courbure voulue... du moins localement en connaissant le rayon de la cheminée et la hauteur h du pas de la spirale):

Figure: 25.12 - Principe de base d'une cheminée industrielle avec spirale
(source: Frank Morgan, Riemmanian Geometry)

ou sa version réelle:

Figure: 25.13 - Cheminée industrielle d'évacuation avec spirale

Mais dans ce cas d'ingénierie, la hauteur h doit être obtenue par une rotation complète. Dès lors le rayon de courbure s'écrit:

  (25.77)

Bref pour en revenir à notre exemple et le finir, il vient par la première formule de Frenet le vecteur normal suivant:

  (25.78)

et dont tous les points (extrémités du vecteur) sont confondus avec l'axe Z de notre hélice quel que soit h! La coordonnée de la composante z de ce vecteur est nulle étant donné que la normale est prise par rapport à un point M de la courbe déjà à une hauteur h implicite.

De par la 3ème formule de Frenet avec le vecteur binormal:

  (25.79)

et le rayon de torsion donné par la relation:

  (25.80)

nous avons donc:

  (25.81)

Et comme nous avons obtenu les trois relations suivantes:

  (25.82)

Nous en déduisons le rayon de torsion:

  (25.83)

E2. Déterminons maintenant le cas important de l'expression explicite du rayon de courbure en coordonnées cartésiennes (résultat utilisé dans le chapitre de Génie Civil et utile dans de nombreux autres domaines de la physique). Considérons pour cela la figure suivante:

Figure: 25.14 - Illustration de l'approche du rayon de courbure en 1D

Nous avons donc le rayon de courbure qui est donné intuitivement par la relation suivante si nous ne faisons pas usage de l'analyse vectorielle:

  (25.84)

Nous avons aussi:

  (25.85)

et comme:

  (25.86)

il vient alors:

  (25.87)

et donc:

  (25.88)

Nous avons démontré dans le chapitre de Calcul Intégral Et Différentiel la dérivée suivante:

  (25.89)

Nous avons alors immédiatement par les dérivées composées:

  (25.90)

Ceci étant fait nous avons aussi besoin de dx/ds. Or, nous avons démontré avec différentes approches dans le chapitre de Mécanique Analytique et Formes Géométriques (entre autres) en utilisant simplement Pythagore que:

  (25.91)

En regroupant le tout nous avons finalement:

  (25.92)

Il vient donc alors le rayon de courbure du cercle localement osculateur d'une fonction cartésienne dans le plan (en prenant la valeur absolue de la dérivée seconde pour éviter d'avoir un rayon négatif...):

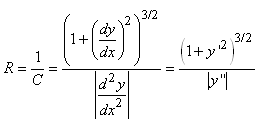  (25.93)

NAPPES PARAMÉTRÉES

Soient :

 avec   (25.94)

Appelons . Si g est continue, alors  est une surface de l'espace "surface d'un seul tenant". Par définition, dans ce qui suit, le couple  où g est une fonction supposée continue sera appelé "nappe paramétrée", et  le "support" de la nappe paramétrée. Nous disons encore que  et  sont des paramétrages de .

Remarquons que pour une surface  (par exemple un disque), il existe plusieurs nappes paramétrées associées (par exemple les coordonnées cartésiennes, polaires, sphériques).

Soit maintenant  et:

  (25.95)  

tels que

Nous pouvons définir :

  (25.96)

Si nous supposons h continue, il est clair que  est un arc paramétré. Appelons  son support, nous avons  et nous disons que est une "courbe tracée" ou "courbe inscrite" sur définie par les "coordonnées de Gauss" u et v (déjà rencontrées dans le chapitre sur les Géométries Non-Euclidiennes).

Remarque: Nous supposerons toujours désormais que

Soit . Intéressons-nous aux deux courbes tracées sur définies par les arcs paramétrés suivants:

 avec

 avec
  (25.97)

et  sont les deux fonctions dites "fonctions partielles" de g en .

Les supports de  et  sont appelés "courbes-coordonnées" de  en  relativement au paramétrage . Nous les notons respectivement  et . Nous appelons aussi  "1ère courbe-coordonnée" et  "2ème courbe-coordonnée".

Il est bien sûr relativement évident (cf. chapitre de Calcul Différentiel Et Intégral) que:

  (25.98)

est tangent à en  et que  est tangent à  en .

Figure: 25.15 - Représentation d'une nappe paramétrée

MÉTRIQUE D'UNE SURFACE

Soit:

 avec   (25.99)

Notons , autrement dit:

  (25.100)

Nous avons aussi (cf. chapitre de Calcul Différentiel Et Intégral):

  (25.101)

et nous avons démontré au début de ce chapitre que l'abscisse curviligne dans un espace cartésien (en coordonnées de Riemann) était donnée par:

  (25.102)

Nous avons donc après substitution en coordonnées de Gauss:

  (25.103)

Ce qui est équivalent à écrire (attention à ne pas y lire qu'on a le carré d'un vecteur mais qu'il s'agit du produit scalaire avec lui-même!):

  (25.104)

De manière plus traditionnelle avec la notation:

  (25.105)

Nous obtenons une relation appelée la "première forme quadratique fondamentale" (nous ne démontrerons pas la deuxième):

  (25.106)

appelée aussi "première forme différentielle de Gauss". Il est intéressant d'écrire cette dernière relation sous la forme:

  (25.107)

et nous voyons que pour que soit positif, il faut alors que E ainsi que soient positifs.

Comme nous l'avons déjà démontré dans le chapitre de Calcul Tensoriel, cette expression est indépendante de la nappe paramétrée  car l'élément de longueur infiniment petit ds est indépendant du paramétrage de . Cette forme quadratique est donc un invariant qui représente la métrique sur . Elle est par ailleurs notée sous la forme suivante par tradition:

  (25.108)

ou de façon encore plus condensée en utilisant la notation tensorielle:

  (25.109)

RÉGULARITÉ D'UNE SURFACE

Définition: Un point M appartenant à la surface  est dit (c'est relativement logique...) "point régulier", si et seulement si:

  (25.110)

Une surface  est logiquement dite "surface régulière", si et seulement si, tous ses points sont réguliers (si le produit vectoriel est nul alors il y a quelque part un "pli" à 90°).

Remarquons que:

  (25.111)

L'angle  entre les deux courbes-coordonnées  et  à  en  est donné par la définition du produit scalaire:

    (25.112)

D'où l'expression:

  (25.113)

Donc une condition nécessaire et suffisant pour que les courbes-coordonnées  et soient perpendiculaires  à  en et que F soit nul. Dans ce cas particulier, on dit que les coordonnées curvilignes u, v sur la surface sont des coordonnées orthogonales.

Exemples:

E1. Considérons le paramétrage du plan cartésien. Nous avons alors:

  (25.114)

d'où:

  (25.115)

Dès lors:

  (25.116)

Nous retrouvons donc la même abscisse curviligne différentielle que celle vue dans le chapitre de Calcul Tensoriel et Relativité Générale avec la métrique diagonale de l'espace plat.

Nous avons aussi:

  (25.117)

Donc, la surface est régulière. Nous avons également:

  (25.118)

Donc, les deux courbes-coordonnées sont perpendiculaires.

E2. Considérons le paramétrage du cylindre. Nous avons alors (cf. chapitre de Calcul Vectoriel):

  (25.119)

d'où:

  (25.120)

Dès lors:

  (25.121)

Nous retrouvons donc la même abscisse curviligne différentielle que celle vue dans le chapitre de Relativité Générale avec la métrique diagonale du plan en coordonnées polaires.

Nous avons aussi:

  (25.122)

Donc, la surface est régulière tant que r est non nul. Nous avons également:

  (25.123)

Donc, les deux courbes-coordonnées sont perpendiculaires sur le cylindre.

E3. Considérons le paramétrage la sphère de centre O et de rayon r. Nous avons alors (cf. chapitre de Calcul Vectoriel):

  (25.124)

d'où:

  (25.125)

Dès lors:

  (25.126)

Nous retrouvons donc la même abscisse curviligne différentielle que celle vue dans le chapitre de Relativité Générale avec la métrique diagonale du plan en coordonnées sphériques.

Nous avons aussi:

  (25.127)

Donc, la surface est régulière tant que r et sont non nuls. Nous avons également:

  (25.128)

Donc, les deux courbes-coordonnées sont perpendiculaires sur la sphère.

E4. Considérons le paramétrage de l'hyperboloïde. Nous avons alors (cf. chapitre de Géométrie Analytique):

  (25.129)

d'où:

  (25.130)

Dès lors:

  (25.131)

Prenons b comme étant nul. Nous avons alors:

  (25.132)

Donc, la surface est régulière tant que a est non nul. Nous avons également:

  (25.133)

Donc, les deux courbes-coordonnées sont perpendiculaires sur l'hyperboloïde.

12   0

Notée par 39 visiteur(s) 12345 PageRater 0.5.0 Commentaires: [0]