News :: Erreur :: Visiteurs :: ClearType :: Imprimer ::

ÉLECTROSTATIQUE | MAGNÉTOSTATIQUE | ÉLECTRODYNAMIQUE | ÉLECTROCINÉTIQUE
OPTIQUE GÉOMÉTRIQUE | OPTIQUE ONDULATOIRE

L'electrodynamique est la partie de la physique qui traite de l'action dynamique des courants électriques (Larousse).

Dernière mise à jour de ce chapitre: 2017-12-31 17:58:01 | {oUUID 1.774}
Version: 3.1 Révision 7 | Avancement: ~90%
vues depuis le 2012-01-01: 39'147

LISTE DES SUJETS TRAITÉS SUR CETTE PAGE

Jusqu'ici nous nous sommes concentrés sur l'interaction gravitationnelle et la grandeur caractéristique de la matière, appelée "masse", qui lui est associée. Nous avons évoqué l'interaction électromagnétique, en analysant des phénomènes macroscopiques, comme le frottement, la cohésion, l'élasticité, les forces de contact, etc. Maintenant nous nous penchons sur les forces électroniques et la caractéristique de la matière, appelée "charge", qui leur est associée. L'interaction électromagnétique lie la matière, sous toutes ses formes observables. C'est elle qui fait tenir les électrons au noyau dans l'atome, qui fait tenir ensemble les atomes dans les molécules, les molécules dans les objets et même votre nez à votre visage (eh oui... nous tenons pas à grand-chose.. lol).

La "charge" produit la "force électrique" ou "force de Coulomb" et nous commençons seulement à comprendre cette force. La charge est une notion fondamentale, qui ne peut pas être décrite en termes de concepts plus simples et plus fondamentaux. Nous la connaissons par ses effets et malheureusement pas par ce qu'elle est (c'est idem pour la masse rappelons-le aussi). 

L'expérience a montré aussi que bien que la charge est comme la masse une propriété additive, elle comporte cependant aussi des valeurs négatives (et non exclusivement positive comme l'est a priori la masse). Ainsi, dans le langage actuel et comme l'expérience le confirme, deux charges identiques se repoussent et deux charges opposées s'attirent.

Voyons maintenant la force qui est associée à la charge:

Force électrique

Il a expérimentalement été établi par Coulomb qu'une particule témoin subit une force d'une intensité proportionnelle à sa charge q, lorsqu'elle est placée au voisinage d'une ou plusieurs charges électriques , dans un milieu de permittivité électrique absolue (permittivité au champ électrique bien sûr...) donnée par (sous forme vectorielle et non relativiste):

  (35.1)

où  est le vecteur position d'une charge témoin.

En d'autres termes, deux corps chargés ponctuels s'attirent ou se repoussent selon une force directement proportionnelle à leur charge et inversement proportionnelle au carré de la distance qui les sépare.

Dans le cas d'un système à deux particules séparées par une distance r, nous avons la même relation simplifiée et nous retrouvons la forme plus commune de la force électrique ou "force de Coulomb" telle qu'elle est donnée dans la plupart des ouvrages (sous forme scalaire et non relativiste):

  (35.2)

La valeur de permittivité électrique dans le vide est quant à elle donnée expérimentalement par:

et relativement au milieu considéré, nous définissons une "permittivité électrique relative" qui permet plus facilement de déterminer les propriétés d'un matériau par rapport au champ électrique tel que nous ayons la "permittivité électrique absolue":

Il convient d'indiquer que certains auteurs définissent la permittivé du vide à partir de la vitesse de la lumière et de la perméabilité magnétique du vide (cf. chapitre de Magnétostatique). Dès lors, la valeur de la permittivité électrique du vide est bien évidemment exacte par définition. Mais cela n'a de sens qu'une fois la théorie de Maxwell connue et celle-ci sera presentée et démontrée que plus tard dans le chapitre d'Électrodynamique (nous suivons les démarches dans l'ordre historique des découvertes scientifiques).

Nous définissons également le rapport:

appelé "constante diélectrique".

Le facteur entre parenthèses dans:

  (35.7)

ne dépend que de la distribution des charges dans l'espace et de la permittivité électrique absolue du milieu considéré. Puisque sa valeur varie d'un endroit à l'autre et dépend du vecteur position de la charge témoin, il forme un ensemble de vecteurs, dont la propriété est celle d'une multitude de lignes de champs électriques d'où l'utilisation du terme "champ électrique". 

L'ensemble de ces vecteurs porte donc le nom de "champ électrique" , au point , dans la distribution de charges :

    (35.8)

Les ingénieurs utilisent souvent une autre notation qui permet de caractériser uniquement la géométrie du champ et ce indépendamment du milieu et introduisent le concept de "champ de déplacement":

nous retrouverons ce vecteur dans le chapitre d'Électrodynamique lors de notre synthèse des équations de Maxwell.

La force Coulombienne, agissant sur la charge témoin q, s'écrit alors de façon conventionnelle: 

  (35.9)

POTENTIEL ÉLECTRIQUE

Soient deux points A et B dans une région de l'espace où il existe un champ électrique  et soit un chemin reliant ces deux points. Alors, dans le cas particulier où la source d'un champ  est une sphère ou un corps ponctuel et que nous posons une charge à son voisinage, nous avons pour le travail effectué par la force pour déplacer la charge du point A au point B:

  (35.10)

Par ailleurs, ce travail est comme nous le verrons plus loin, assimilable à l'énergie potentielle. Nous définissons ainsi la "différence de potentiel" ou simplement le "potentiel" par la relation:

et donc:

Démontrons maintenant dans le cadre le plus général qui soit que le champ vectoriel stationnaire dérive d'un champ de potentiel:

Soit une charge Q repérée par rapport à un référentiel par le vecteur . Alors en chaque point de l'espace, il existe un champ  tel que:

    (35.13)

développons cette expression:

  (35.14)

Si   est un champ de potentiel stationnaire alors, il doit exister un potentiel de ce champ qui satisfasse:

  ;;   (35.15)

Regardons si le potentiel existe pour un champ de Coulomb. Nous devons alors avoir pour le champ en x:

  (35.16)

d'où:

  (35.17)

et si nous effectuons le même développement pour chaque composante, nous obtenons également le même résultat. Donc le potentiel électrique est un champ scalaire et non vectoriel (le champ électrique est donc lui un champ vectoriel)!

Le pontentiel est appelé dans le cas d'un champ de Coulomb "potentiel coulombien" et est par convention choisi tel que:

  (35.18)

Comme nous pouvons le constater par l'expression de antéprécédente, C est une constante arbitraire, qui impose dans le cas d'absence de charges que:

  (35.19)

Ce qui nous donne finalement: 

  (35.20)

Ce qui donne pour toutes les composantes:

    (35.21)

que nous notons plus brièvement:

  (35.22)

Il s'ensuit donc que:

  (35.23)

et donc par exemple pour un potentiel ponctuel à symétrie sphérique (cas que nous retrouvons dans de nombreux autres chapitres), il vient alors:

  (35.24)

Indépendance du chemin

Démontrons maintenant que la différence de potentiel entre deux points A et B ne dépend pas du chemin parcouru tel que nous l'avons fait pour le champ de potentiel gravitationnel dans le chapitre de Mécanique Classique.

Soit un chemin reliant deux points A et B et un champ  et faisons en sorte d'exprimer le champ en x, y et z par rapport à une seule variable t (qui n'a rien avoir avec le temps...) qui rendrait compte de sa variation lors d'un déplacement quelconque entre ces deux points:

  (35.25)

avec donc A qui correspondrait à la valeur du paramétrage et B à la valeur .

Or, nous savons que (cf. chapitre de Calcul Différentiel et Intégral et Calcul Vectoriel):

  (35.26)

Il vient alors:

  (35.27)

Dès lors:

  (35.28)

Cette dernière expression montre bien que U est indépendant du chemin quelle que soit la manière dont nous paramétrons celui-ci. 

Le champ de Coulomb est donc un "champ conservatif". En effet, si nous considérons un chemin fermé  et soient A et B deux points confondus du chemin alors la différence de potentiel sera nulle.

Signalons que parfois nous disons aussi que le champ gradient du potentiel est conservatif.

ÉQUIPOTENTIELLES ET LIGNES DE CHAMP

Nous pouvons maintenant à partir de ce que nous avons établi, définir les "équipotentielles" et les "lignes de champ".

Soit un champ de Coulomb défini par rapport à un référentiel. Alors à chaque point (x,y,z) de l'espace, nous pouvons associer un vecteur champ électrique  ainsi qu'un potentiel électrique.

Définition: Nous définissons les "lignes de champ" comme étant une famille de courbes pour lesquelles le vecteur est tangent et constant en chaque point et les "équipotentielles" comme étant des lignes pour lesquelles le potentiel U(x,y,z) est aussi constant. 

Dans ce cas, et c'est ce que nous allons démontrer, toutes les lignes de champ sont perpendiculaires à toutes les équipotentielles.

Démonstration:

Utilisons la propriété suivante de conservation du champ de Coulomb pour la démonstration:

  (35.29)

Comme nous sommes en présence d'un champ électrique, celui-ci dérive donc d'un potentiel comme nous le savons. Ceci implique que si le champ n'est pas nul le potentiel ne l'est également pas. Donc, dans l'intégrale curviligne:

    (35.30)

un des termes est nul ! Ce n'est pas le champ électrique puisqu'on est présence d'un, ce qui discrédite le potentiel U et comme la charge se déplace  n'est pas nul non plus. Écrivons alors l'intégrale curviligne d'une autre manière:

  (35.31)

d'où:

    (35.32)

nous pouvons donc conclure que les équipotentielles sont bien perpendiculaires aux lignes de  champ électrique et inversement. C'est ce qu'il fallait démontrer.

Voici des exemples de lignes de niveaux comprenant lignes de champ et lignes de potentiel obtenus à l'aide de Maple  4.00b (nous montrerons lors de notre étude des équations différentielles comment obtenir les fonctions mathématiques des lignes de champ):

Figure: 35.1 - À gauche: une seule charge - À droite: deux charges de même signe

Figure: 35.2 - À gauche: deux charges de signes opposés - À droite: quatre charges de même signe

Deux applications de ces résultats sont très importantes (pour lesquelles nous nous limiterons à l'étude des propriétés les plus importantes):

1. La détermination des lignes de champ et des lignes équipotentielles pour un fil rectiligne infini tel que nous pouvons en approximation en considérer dans les circuits électriques ou les lignes hautes tensions aériennes (afin de déterminer l'influence des champs des fils avec leur environnement - cette étude fait partie du domaine de l'électrodynamique de l'ingénieur que nous appelons la CEM pour "Compatibilité Électromagnétique").  Les résultats pourront aussi être utilisés pour déterminer la "tension de pas" pour certains systèmes rectilignes qui détermine pour une distance donnée, le potentiel par mètre pour lequel un mammifère peut être tué par électrochoc à proximité d'un tel fil. Une extension (sur laquelle je ne souhaite pas trop m'attarder bien que le sujet soit passionnant mais très chaud) est aussi l'influence d'un tel type de potentiel sur le fonctionnement du cerveau humain dans le cas de l'usage des téléphones portables (antennes émettrices d'un potentiel) ou d'habitations proches de lignes hautes tensions....

2. La détermination des lignes de champ et équipotentielles du dipôle électrique a une énorme importance en chimie. Nous verrons également quelle est la dynamique de celui-ci lorsqu'il est plongé dans un champ électrique uniforme et l'énergie d'interaction entre dipôles (comme c'est souvent le cas en chimie).

FIL RECTILIGNE INFINI

Soit:

  (35.33)

Nous avons:

  (35.34)

en faisant usage du concept de densité linéique de charges telle que nous l'avons définie dans le chapitre Principes de la section de Mécanique, nous avons:

  (35.35)

Considérons une ligne infinie de section négligeable, et portant une charge linéique continue . Le but est donc de calculer le champ électrique et le potentiel en tout point M de l'espace extérieur à cette ligne afin de connaître les influences des charges de cette ligne sur son environnement en ne considérant que l'influence du champ électrique (si les charges étaient en mouvement il faudrait également prendre en compte l'influence du champ magnétique, ce que nous ferons dans le chapitre de Magnétostatique).

Pour cela, la méthode consiste à découper la ligne en de petits éléments de ligne dl, chacun de ces éléments portant une charge dq. Le champ créé par la charge en P au point M situé à distance x et de projection orthogonale H sur la ligne est:

  (35.36)

L'astuce consiste maintenant à prendre le symétrique P' de P par rapport à H (la projection orthogonale de M sur le fil):

Figure: 35.3 - Configuration de l'analyse du fil rectiligne infini

pour lequel nous avons identiquement:

  (35.37)

Le champ total est donc:

  (35.38)

Or, nous avons:

  (35.39)

Donc:

  (35.40)

Comme nous pouvons nous en douter, cette dernière relation montre bien que le champ est orthogonal à la ligne (au fil...).

La norme de est:

  (35.41)

Cette relation comporte 3 variables dépendantes r,dl,x. La norme du champ total en un point est donc la somme des normes sur l'ensemble de la longueur du fil puisque tous les vecteurs ont même direction.

Pour effectuer ce calcul, nous allons effectuer un changement de variable, et mettre r,dl,x en fonction de l'angle entre la ligne et le vecteur . Dans le triangle rectangle HMP:

  (35.42)

si nous prenons l'origine des z en H. Nous avons aussi:

  (35.43)

et:

  (35.44)

d'où:

  (35.45)

L'intégration est facile, mais il faut faire attention aux bornes. Nous devons intégrer sur une moitié de ligne, donc entre 0 et :

  (35.46)

et alors:

  (35.47)

Le potentiel se déduit aisément en prenant la primitive de E puisque:

  (35.48)

Nous avons alors:

  (35.49)

La constante est indéterminée puisque lorsque r tend vers l'infini, U tendant vers zéro conduit à une constante infinie. Cette indétermination est due essentiellement à l'approximation de la ligne infinie.

DIPÔLE ÉLECTRIQUE RIGIDE

Une disposition des charges très intéressante est celle constituant un "dipôle" électrique appelé rigoureusement "dipôle électrique rigide" ou "dipôle électrostatique". Elle consiste en deux charges égales et opposées +q,-q séparées par une très petite distance. Nous allons chercher à déterminer le potentiel et le champ électrique en un point M de l'environnement du dipôle.

Pour déterminer cela, considérons une charge quelconque en un point et un point M très éloigné de . Prenons un repère quelconque centré en O:

Figure: 35.4 - Champ électrique en un point M très éloigné du dipôle

Le potentiel créé au point M par la charge s'écrit:

  (35.50)

Dans le triangle , la distance peut être écrite selon le théorème du cosinus:

  (35.51)

Le potentiel devient:

  (35.52)

ou encore:

  (35.53)

À très grande distance, r devient très supérieur à , la quantité:

  (35.54)

tend alors vers zéro. Nous pouvons donc effectuer un développement de Maclaurin (cf. chapitre sur les Suites Et Séries) de au voisinage de . Pour ne pas alourdir le calcul, nous nous limiterons à l'ordre deux en r:

  (35.55)

donc:

  (35.56)

En ne gardant que les termes du second ordre en r:

  (35.57)

Le potentiel devient:

  (35.58)

Nous avons gardé dans l'expression du potentiel trois termes. Le terme est le potentiel créé par une charge qui se trouverait en O. Autrement dit, à l'ordre zéro, le potentiel créé par une charge située en un point proche de O est identique au potentiel créé par une charge qui se trouverait en O. Les termes sont des termes correctifs, à l'ordre un et à l'ordre deux respectivement. Nous remarquons que ces deux termes varient en , donc décroissants plus vite que le premier. Ces deux termes sont donc plus efficaces à plus petite distance.

Nous voyons que les termes font intervenir la quantité . Cette quantité est ce que nous définissons comme étant le "moment dipolaire" du dipôle électrostatique:

  (35.59)

Le potentiel créé à grande distance par une distribution discrète de charges s'obtient en sommant toutes les contributions individuelles:

  (35.60)

Ce qui peut aussi s'écrire:

  (35.61)

Par définition, est le terme unipolaire ou monopolaire, le terme dipolaire, quadripolaire. Si la distribution de charge est au total nulle, comme c'est le cas d'un atome ou d'une molécule non ionisée, seuls subsistent les contributions multipolaires.

Revenons au cas particulier du dipôle:

Le terme monopolaire y est nul, puisque la somme des charges est nulle. Si nous négligeons les termes d'ordre supérieur au premier, il reste la contribution dipolaire.

Les angles et du dipôle sont complémentaires, donc . Mais, comme , le produit est constant.

Les deux charges du dipôle sont à une distance constante l'une de l'autre et à équidistance de l'origine O. Nous poserons que .

Le potentiel se réduit alors à:

  (35.62)

où a est simplement la distance constante entre les deux charges.

Il est d'usage dans le cas de l'étude du dipôle électrique d'écrire la relation précédente sous la forme:

  (35.63)

où est la définition de moment dipolaire et:

  (35.64)

Rappelons maintenant que nous avons démontré au début de ce chapitre que:

  (35.65)

et comme nous l'avons vu dans le chapitre de Calcul Vectoriel, le gradient en coordonnées sphériques nous amène à écrire:

  (35.66)

d'où:

  (35.67)

Pour déterminer l'équation des équipotentielles, rappelons que ces lignes (ou "surfaces" dans l'espace) s'obtiennent par la contrainte:

  (35.68)

d'où:

  (35.69)

avec:

  (35.70)

Le champ électrique doit être par définition tangent aux lignes de champ, donc parallèle au déplacement élémentaire.

  (35.71)

Puisque , nous avons:

  (35.72)

Donc finalement il ne reste plus que:

  (35.73)

Qui est donc une équation différentielle qui s'intègre facilement:

  (35.74)

Ce qui équivaut à écrire:

  (35.75)

Le tracé des lignes de champ et des équipotentielles donne alors en coordonnées sphériques (ne pas oublier que la composante verticale est nulle par symétrie):

Figure: 35.5 - Tracé des lignes de champ d'un dipôle électrique

Bien que dans un dipôle électrique les deux charges soient égales et opposées, donnant une charge résultante nulle, le fait qu'elles soient légèrement déplacées est suffisant pour produire un champ électrique non identiquement nul. Dans les atomes, le centre de masse des électrons coïncide avec le noyau, et par conséquent le moment électrique dipolaire moyen de l'atome est nul. Mais si un champ extérieur est appliqué, le mouvement des électrons est distordu et le centre de masse des électrons est déplacé d'une distance x par rapport au noyau. L'atome est alors polarisé et devient un dipôle électrique de moment p. Ce moment étant proportionnel au champ extérieur .

Voilà un code Maple 17.00 pour s'amuser:

>V:=1/sqrt((x-1)^2+y^2+z^2)-2/sqrt((x+1)^2+y^2+z^2):
>with(LinearAlgebra); with(VectorCalculus); with(plots);
>with(plottools);
>Efield := Gradient(-V, [x, y, z]);
>fieldplot3d([Efield[1], Efield[2], Efield[3]],x =-1.5..1.5, y =-1.5..1.5, z =-1.5..1.5);
>NormEfield := Normalize(Efield,2);
>p1:=sphere([1, 0, 0],0.75,color=red);
>p2:=sphere([-1, 0, 0],1.5,color=blue);
>p3:=fieldplot3d(NormEfield,x=-4.5..4.5,y=-4.5..4.5,z =-4.5..4.5,color=black);
>display([p1, p2, p3], scaling = constrained);

Ce qui donne dans un premier temps (évidemment les dimensions sont fictives):

Figure: 35.6 - Lignes de champ électrique pour deux charges de signes opposés

>z:= 0;
>plot3d(V,x =-1.5..1.5, y=-1.5..1.5, style=patchcontour,contours=200);

Figure: 35.7 - Profil du potentiel et lignes équpotentielles du dipôle

>p4:=implicitplot({seq(V = (1/10)*b,b=-10..10)},x=-5..5,y=-4..4);
>p5 := fieldplot([NormEfield[1], NormEfield[2]], x = -5 .. 5, y = -4 .. 4); display([p4, p5], scaling = constrained);

Figure: 35.8 - Profil 2D du potentiel et du champ électormagnétique du dipôle

Remarque: Les molécules par ailleurs peuvent avoir un moment électrique permanent. De telles molécules sont dites "molécules polaires". Par exemple, dans la molécule HCl l'électron de l'atome d'hydrogène passe plus de temps à se déplacer autour de l'atome de chlore qu'autour de l'atome d'hydrogène. Aussi, le centre des charges négatives ne coïncide-t-il pas avec le centre des charges positives et la molécule possède un moment dipolaire. Par contre, dans la molécule , tous les atomes sont alignés, et le moment électrique dipolaire résultant est nul par raison de symétrie.

Quand un dipôle électrique est placé dans un champ électrique, une force s'exerce sur chacune des charges du dipôle. La force résultante est:

  (35.76)

Considérons le cas particulier où le champ électrique est dirigé le long de l'axe des X et où le dipôle est orienté parallèlement à ce champ. Si nous considérons seulement les grandeurs:

  (35.77)

avec a étant la distance entre les deux charges, et par conséquent:

  (35.78)

Ce résultat montre qu'un dipôle électrique orienté parallèlement au champ tend à se déplacer dans la direction dans laquelle le champ s'accroît (selon le gradient de celui-ci). Nous remarquons que si le champ électrique est uniforme, la force résultante sur le dipôle est nulle.

L'énergie potentielle du dipôle est:

  (35.79)

Si nous utilisons la relation:

  (35.80)

pour décrire le champ électrique uniforme et si est l'angle entre le dipôle et le champ électrique, le dernier facteur est juste la composante du champ parallèle à . Donc:

  (35.81)

ou

  (35.82)

L'énergie potentielle est minimale pour , ce qui montre que le dipôle est en équilibre quand il est orienté parallèlement au champ.

Ces configurations d'un dipôle placé dans un champ électrique ont des applications très importantes. Par exemple, le champ électrique d'un ion en solution polarise les molécules du solvant qui entoure les ions et elles s'orientent comme sur la figure ci-dessous:

Figure: 35.9 - Exemple de ce qui se passe dans une solution avec un ion

Dans un solvant à molécules polaires tel que l'eau, les ions d'un électrolyte en solution s'entourent d'un certain nombre de ces molécules en raison de l'interaction charge-dipôle. Ce phénomène est appelé la "solvation" de l'ion, précisément "hydratation" si le solvant est de l'eau.

Ces molécules orientées deviennent plus ou moins solidaires de l'ion, augmentant sa masse effective et diminuant sa charge effective, qui est partiellement masquée par les molécules. L'effet net est que la mobilité de l'ion dans un champ extérieur est réduite. De même, lorsqu'un gaz ou un liquide, dont les molécules sont des dipôles permanents est placé dans un champ électrique, les molécules à la suite des couples dus au champ électrique, tendent à s'aligner avec leurs dipôles parallèles. Nous disons alors que la substance a été "polarisée".

Il peut donc être intéressant de déterminer le champ électrique vectoriel produit par un dipôle plutôt que le potentiel. Le champ électrostatique créé en un point M par le doublet s'obtient en effectuant la somme vectorielle des champs créés en ce point par des charges positive P et négative N, d'où:

  (35.83)

La distribution des charges étant invariante par rotation autour de l'axe Oz du doublet, la topographie est indépendante de l'angle azimutal des coordonnées sphériques. Nous pouvons la représenter dans un plan méridien quelconque passant par l'axe NP. Le champ est donc donné par:

  (35.84)

Ayant:

  (35.85)

vectoriellement, nous avons:

  (35.86)

Le produit scalaire étant la multiplication des composantes une à une, nous avons:

  (35.87)

d'où:

  (35.88)

Finalement:

  (35.89)

Donc par un développement limité en série de Maclaurin comme nous l'avons fait au début:

  (35.90)

soit en introduisant :

  (35.91)

Il peut être pertinent aussi de calculer l'énergie d'interaction entre deux dipôles électriques. Si nous appelons le moment dipolaire, nous pouvons écrire:

  (35.92)

Si nous désignons par le moment du second dipôle et si nous utilisons la relation:

  (35.93)

nous trouvons que l'énergie d'interaction entre les deux dipôles est:

  (35.94)

Nous pouvons tirer plusieurs conclusions importantes de ce résultat. L'énergie d'interaction est symétrique par rapport aux deux dipôles, car la permutation de et la laisse inchangée. C'est un résultat prévu. L'interaction entre deux dipôles n'est pas centrale car elle dépend des angles que le vecteur de position ou le vecteur unitaire fait avec et .

Un atome, une molécule ou un ion, dont le moment dipolaire est nul à l'état fondamental, acquièrent un moment dipolaire sous l'action du champ électrique appliqué comme nous l'avons vu puisque les charges de signes opposées sont sollicitées dans des sens opposés. Les barycentres des charges positives et négatives ne coïncidant plus, il apparaît un "moment dipolaire induit". Dans une approximation expérimentale linéaire valable pour des champs excitateurs faibles, ce moment dipolaire induit est proportionnel au champ appliqué , ce que nous traduisons par (il s'agit au fait d'une approximation de la relation de Langevin-Debye que nous démontrerons plus tard):

  (35.95)

La quantité , dont la dimension physique est celle d'un volume, est la "polarisabilité" de l'édifice. L'interaction électrostatique dipôle-dipôle a été introduite par J.D. Van der Waals en 1873, dans le cas des molécules, afin d'interpréter les écarts réels par rapport aux gaz parfaits.

Les forces de Van der Waals sont répulsives lorsque la distance entre les molécules est très faible car elles s'opposent à l'interpénétration des nuages électroniques, ce que nous exprimons en introduisant leur volume (covolume).

En revanche, elles sont attractives lorsque cette distance est suffisante. Nous attribuons cette attraction à trois types d'interaction mettant en cause des dipôles rigides ou induits:

1. Les forces entre molécules polaires (dipôles rigides), dites de W. Keesom.

2. Les forces entre une molécule polaire (dipôle rigide), et une molécule polarisable (dipôle induit) dites de Debye.

3. Les forces moyennes entre les dipôles induits instantanés qui apparaissent même lorsque les molécules ne sont pas polaires, dites de F. London.

Dans ces trois cas, l'énergie électrostatique est négative (attraction) et varie comme . Pour le montrer, calculons l'énergie d'interaction entre deux dipôles rigides, de moments dipolaires et :

  (35.96)

avec:

  (35.97)

et:

  (35.98)

Par conséquent:

  (35.99)

d'où:

  (35.100)

Ainsi, la dépendance radiale de la force est en . Cette décroissance très rapide de la force de Van der Waals avec la distance permet d'expliquer sa très courte portée et par conséquent son influence lorsque le milieu est suffisamment dense.

FLUX DU CHAMP ÉLECTRIQUE

Soit un champ vectoriel et S une surface appelée "surface de Gauss" dans l'espace. Si nous divisons cette surface en un nombre N de petites surfaces dS chacune traversée par un champ  et ayant un vecteur unitaire  perpendiculaire (cas particulier) à leur surface, nous pouvons alors former la somme:

  (35.101)

Lorsque N tend vers l'infini et tous les dS vers zéro, nous obtenons pour cette somme:

  (35.102)

La valeur de cette intégrale donne donc le flux du champ à travers la surface S délimitée par un domaine  et où:

  (35.103)

Dans le cas du champ électrostatique, nous écrivons:

  (35.104)

Cette expression définit le "flux électrique".

La question inévitable qui se pose alors est: quelle est sa signification physique ? Le flux d'un fluide est la quantité de fluide (notamment le volume) qui traverse une surface par seconde; il y alors écoulement de quelque chose. Quant au flux électrique, du point de vue classique, rien ne s'écoule, le champ électrique est déjà établi et il est statique, mais il traverse la surface. La valeur du champ électrique en tout point de l'espace est l'intensité du champ en ce point, tandis que le flux peut être considéré comme la quantité de champ qui traverse la surface S. Il y a une centaine d'années, les physiciens identifiaient le flux avec le nombre des lignes de champ traversant la surface. Mais le moins que nous puissions dire est que la vision simpliste que les lignes de champ ont une réalité distincte et que nous pouvons les compter est trompeuse. Nous verrons en mécanique quantique des champs que celle-ci soutient qu'un courant de photons virtuels est la nature même des interactions électromagnétiques. Malgré cela, les physiciens ne se sont pas pressés d'associer le flux des photons virtuels du 20ème siècle à l'image des lignes de champ continues du 19ème siècle. Quelle que soit sa nature, la notion de flux est puissante et de grande utilité pratique, aussi bien en électricité qu'en magnétisme.

Comme nous le démontrerons dans le cadre des équations de Maxwell (cf. chapitre d'Électrodynamique), la résolution de cette intégrale est (c'est la "loi de Gauss" ou également dit "théorème de Gauss"):

  (35.105)

CAPACITÉS

Comme application directe du théorème de Gauss, très utile en électronique et pour les ingénieurs, considérons une grande feuille mince et plane, portant une charge surfacique homogène et baignant dans un milieu de permittivité électrique absolue . Dans la région proche de son centre, le champ résultant de tous les champs des charges est normal, uniforme, constant et s'éloigne de la feuille. Considérons une surface de Gauss en forme d'un cylindre limité par les bases et sa surface tubulaire et symétrique par rapport à la feuille. Elle enferme donc une charge . Il en résulte que:

  (35.106)

et comme et , nous trouvons:

  (35.107)

Finalement, le champ électrique d'une grande feuille chargée plane et mince est:

  (35.108)

Si nous mettons face à face deux plaques identiques mais avec des charges opposées, la somme algébrique donnera bien évidemment:

  (35.109)

À l'exception des extrémités, où l'effet de bord est important, le champ global est partout la somme vectorielle des champs uniformes produits par les deux couches minces opposées. Nous appelons un tel système un "condensateur plan et parallèle".

Figure: 35.10 - Exemple de condensateur plan et parallèle

Le résultat est aussi remarquable, car il est indépendant de la distance d entre les plans. Le calcul du potentiel électrique y est donc simplifié. Soit:

  (35.110)

Ainsi, la capacité du condensateur plan et parallèle vaut donc:

  (35.111)

Voyons un deuxième exemple scolaire qu'est le "condensateur cylindrique":

Les armatures d'un condensateur cylindrique sont deux cylindres infinis (ou très grands relativement à leur diamètre) coaxiaux de rayon  et . Il s'agit donc du cas très important du câble coaxial (dont le diélectrique est souvent du polyéthylène) que l'on retrouve dans de nombreux laboratoires:

Figure: 35.11 - Exemple de condensateur cylindrique

Par le théorème de Gauss, nous savons que:

  (35.112)

Et puisque le champ est colinéaire en tout point à la surface, il vient immédiatement en connaissant l'expression de la surface du cylindre (cf. chapitre Formes Géométriques):

  (35.113)

Or:

  (35.114)

Et donc,

  (35.115)

Calculons aussi la capacité d'un condensateur sphérique qui correspond en première approximation à certains générateurs de Van Der Graaf que nous avons dans les labos de quelques écoles, de musées ou même de centres de recherche:

Un "condensateur sphérique" est constitué de deux sphères concentriques de rayon  et  avec .

Figure: 35.12 - Exemple de condensateur sphérique

Nous avons maintenant immédiatement:

  (35.116)

Et donc puisque le champ est colinéaire en tout point à la surface il vient immédiatement en connaissant l'expression de la surface d'une sphère:

  (35.117)

Or:

  (35.118)

Nous avons alors:

  (35.119)

Donc, nous avons alors:

  (35.120)

Voilà pour les exemples classiques....

Nous venons donc de voir que la capacité était définie par:

  (35.121)

soit en régime non continu (cf. chapitre d'Électrocinétique):

  (35.122)

Nous avons alors pour la puissance instantanée (cf. chapitre d'Électrocinétique):

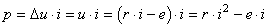  (35.123)

En supposant un condensateur idéal (qui ne dissipe pas d'énergie par effet Joule) il vient:

  (35.124)

Donc par intégration dans un intervalle de temps donné de 0 à t nous avons:

  (35.125)

Cette énergie est donc toujours positive et est stockée sous forme électrostatique dans le condensateur.

Dans le cadre d'un régime sinusoïdal, la puissance moyenne sera nulle. Nous pouvons généraliser ceci en admettant qu'un condensateur parfait ne dissipe aucune puissance par effet Joule.

RIGIDITÉ DIÉLECTRIQUE

La "rigidité diélectrique" d'un milieu isolant représente la valeur maximum du champ en que le milieu peut supporter avant le déclenchement d'un arc électrique (donc d'un court-circuit). Pour un condensateur utilisé en électronique, si nous dépassons cette valeur, nous observons la destruction de l'élément. Cette valeur maximale de la tension appliquée aux bornes, est appelée "tension de claquage" du condensateur. Nous pouvons définir la rigidité du milieu comme étant:

  (35.126)

Exemple:

Pour l'air, on trouve dans les tables la valeur:

  (35.127)

Lorsque nous parlons de rigidité diélectrique, nous parlons aussi du diélectrique qui est un isolant ou une substance qui ne conduit pas l'électricité et qui est polarisable par un champ électrique. Dans la plupart des cas, les propriétés du diélectrique sont dues à la polarisation de la substance. Lorsque le diélectrique (dans notre cas, l'air est le diélectrique) est placé dans un champ électrique, les électrons et les protons de ses atomes se réorientent et, dans certains cas, à l'échelle moléculaire, une polarisation est induite (comme nous l'avons vu lors de notre étude des dipôles). Cette polarisation engendre une différence de potentiel, ou tension, entre les deux bornes du diélectrique; celui-ci emmagasine alors de l'énergie qui devient disponible lorsque le champ électrique est supprimé. L'efficacité d'un diélectrique est sa capacité relative à emmagasiner de l'énergie comparée à celle du vide. Elle s'exprime par la permittivité électrique relative, déterminée par rapport à celle du vide. La force diélectrique est la capacité d'un diélectrique à résister aux champs électriques sans perdre ses propriétés isolantes. Un diélectrique efficace libère une grande partie de l'énergie qu'il a emmagasinée lorsque le champ électrique est inversé.

ÉNERGIE POTENTIELLE ÉLECTROSTATIQUE

Considérons deux charges . La première est supposée au repos et fixe; la deuxième est amenée de l'infini à une distance a de (le même raisonnement a été appliqué pour le champ gravitationnel dans le chapitre de Mécanique Classique). Supposons que les deux charges soient de même signe. Comme ont tendance à se repousser mutuellement, il faut fournir une énergie potentielle pour approcher (infiniment lentement) de . Le travail dW fourni par la force électrostatique en un point quelconque est par définition:

  (35.128)

L'énergie potentielle du système est:

  (35.129)

car F est résistant (d'où l'origine du signe "-").

Donc:

  (35.130)

Nous obtenons alors simplement l'énergie potentielle en un point (donc le x au numérateur se simplifie avec un des x au dénominateur) au signe près:

  (35.131)

Cette énergie potentielle peut donc être négative ou positive.

Cela n'empêche pas que pour avoir la variation d'énergie potentielle, il faut intégrer la relation antéprécédente.

Ainsi que la relation:

  (35.132)

Remarquons que l'avant-dernière relation peut aussi se mettre sous la forme:

  (35.133)

- Électricité et Magnétisme, Resnick/Halliday, Éditions ERPI, ISBN-10: 2761300196 (299 pages) - Imprimé en 2003

24   2

Notée par 84 visiteur(s) 12345 PageRater 0.5.0 Commentaires: [1]