|

ASTRONOMIE | ASTROPHYSIQUE | RELATIVITÉ RESTREINTE
RELATIVITÉ GÉNÉRALE | COSMOLOGIE | THÉORIE
DES CORDES
La
cosmologie est la science qui étudie la structure, l'évolution
et les lois générales de l'Univers considéré
dans son ensemble (Larousse).
| 47.
ASTRONOMIE (MÉCANIQUE
CÉLÉSTE) |
Dernière mise à jour
de ce chapitre:
2017-12-31 17:56:14 | {oUUID 1.725}
Version: 3.3 Révision 15 | Avancement: ~80%
 vues
depuis le 2012-01-01:
0 vues
depuis le 2012-01-01:
0
 LISTE DES SUJETS TRAITÉS SUR CETTE PAGE
LISTE DES SUJETS TRAITÉS SUR CETTE PAGE
La
mécanique céleste est la
conséquence de la loi d'attraction universelle de Newton
et du principe fondamental de la mécanique (cf.
chapitre de Mécanique Classique). Elle a pour principal
objectif la description du mouvement d'objets astronomiques tels
que les étoiles et planètes à l'aide des théories
physiques et mathématiques.
Nous allons dans ce chapitre aborder le sujet, comme toujours
sur ce site, de la manière la plus élémentaire
possible (à ce jour les sujets traités sur cette
page ne dépassent
pas techniquement le niveau de ce qui se faisait au milieu du 18ème
siècle
dans le
domaine de l'astronomie).
D'abord,
nous nous échaufferons avec une loi sympathique sur le
vivant dans l'Univers... (l'équation de Drake). Une
fois cet exercice de style accompli,
nous commencerons à "énumérer" les
lois de Kepler (en faisant souvent référence
au chapitre de Mécanique Classique) pour ensuite
étudier
en détails les propriétés des orbitales
Képlériennes à l'aide
de la mécanique et ensuite à l'aide de la relativité restreinte,
ce
qui nous amènera à constater une précession
théorique des orbitales
concernées. Ensuite, nous nous amuserons à modéliser
approximativement la variation de la durée de la journée
(et de la nuit) sur la Terre en fonction du mois et de la latitude.
Enfin, pour terminer en beauté, nous nous lancerons dans
le calcul détaillé des cinq points de Lagrange!
ÉQUATION DE DRAKE
Cette équation a été inventée (...)
par F. Drake dans les années 1960 dans l'intention d'estimer
le nombre de civilisations extraterrestres dans notre galaxie
avec lesquelles nous pourrions entrer en contact. Le principal
objet de cette équation
pour les scientifiques est de déterminer ses facteurs, afin
de connaître le nombre probable et (très) estimé de
civilisations extraterrestres.
Cette équation empirique
(qui reste un amusement... et dont le principe peut être appliqué
à pas mal de domaines différents de la physique et de la vie...)
s'écrit:
 (47.1)
(47.1)
Les termes de cette formule
(car c'en est une!) se définissent ainsi:
-  représente
le nombre d'étoiles dans une seule et unique galaxie représente
le nombre d'étoiles dans une seule et unique galaxie
-  est
la fraction d'étoiles qui auraient une planète
en orbite (comprise entre 0 et 1) est
la fraction d'étoiles qui auraient une planète
en orbite (comprise entre 0 et 1)
-  est
le nombre de planètes par étoile qui remplissent les conditions
au développement de la vie est
le nombre de planètes par étoile qui remplissent les conditions
au développement de la vie
-  est
la fraction de planètes dont la vie s'est effectivement
développée (comprise entre 0 et 1) est
la fraction de planètes dont la vie s'est effectivement
développée (comprise entre 0 et 1)
-  est
la fraction de celles où une vie intelligente s'est
développée
(comprise entre 0 et 1) est
la fraction de celles où une vie intelligente s'est
développée
(comprise entre 0 et 1)
-  est
la fraction de est
la fraction de  qui
a mis en oeuvre des moyens de communication radio (comprise
entre 0 et 1) qui
a mis en oeuvre des moyens de communication radio (comprise
entre 0 et 1)
-  est
la fraction de temps pendant laquelle les civilisations est
la fraction de temps pendant laquelle les civilisations  vivront
(comprise entre 0 et 1) vivront
(comprise entre 0 et 1)
Dans la pratique, il faut remarquer que l'équation consiste à essayer
de déterminer une quantité inconnue à partir
d'autres quantités qui sont tout aussi inconnues qu'elles...
Mais c'est une équation sympa à sortir et à évaluer
entre amis pour passer le temps...
Il n'existe donc pas de garantie que l'on soit davantage fixé après
cette estimation qu'avant (argument nommé parfois dans la
littérature "garbage in, garbage out"...).
La valeur résultante peut motiver que les développements
qui vont suivre ne sont pas applicables qu'à un seul système
solaire dans l'Univers... peut-être... (cela ferait beaucoup
de vide gâché
sinon...).
LOIS
DE KEPLER
En astronomie, les lois de Kepler décrivent les propriétés
principales du mouvement des planètes autour d'un astre
principal, sans les expliquer (à l'époque!). Elles
ont été découvertes
par Johannes Kepler à partir des observations et mesures
(en quantité phénoménale) de la position des
planètes
faites par Tycho Brahe,
mesures qui étaient très précises pour l'époque.
Les deux premières lois de Kepler furent publiées
en 1609 et la troisième en 1618. Les orbites elliptiques,
telles qu'énoncées dans ses deux premières
lois, permettent d'expliquer la complexité du mouvement
apparent des planètes.
Peu après, Isaac Newton découvrit en 1687 la loi
de l'attraction gravitationnelle (ou gravitation), déduisant de
celle-ci, par le calcul, les 3 lois de Kepler.
Nous allons maintenant nous efforcer de présenter
ces lois de la manière la plus pertinente possible:
PREMIÈRE
LOI
La "première
loi de Kepler", appelée parfois aussi "loi
de conicité"
ou encore "loi des orbites"
s'énonce
ainsi: Les orbites des planètes sont des coniques (ellipses)
dont le Soleil occupe
l'un des
foyers.
Au fait, il convient de
préciser que ce n'est pas vraiment une "loi" dans
le sens propre du terme puisque plus loin vous en trouverez
la démonstration
telle que:
 (47.2)
(47.2)
Remarque: Le lecteur qui aura lu au préalable le
chapitre de Géométrie Analytique ne sera pas étranger
à cette relation...
DEUXIÈME
LOI
La "deuxième
loi de Kepler", appelée parfois aussi "loi
des aires", nous dit que le segment
qui joint une planète au Soleil balaie des aires égales en
des temps égaux (vitesse aréolaire constante) tel que:
 (47.3)
(47.3)
C'est une relation qui découle
de la conservation du moment cinétique comme nous l'avons
déjà démontré dans le chapitre de
Mécanique Classique où nous avions obtenu:
 (47.4)
(47.4)
Donc à nouveau,
son statut de "loi" est
discutable dans le langage de la physique moderne!
Exprimons maintenant cette loi sous une autre forme plus conventionnelle
en astronomie. Considérons pour cela le mouvement dans le plan
données en coordonnées cylindriques par:
 (47.5)
(47.5)
Donc:
 (47.6)
(47.6)
Il vient alors de par la propriété de linéarité du
produit vectoriel:
 (47.7)
(47.7)
Soit en prenant la norme:
 (47.8)
(47.8)
Et puisque c'est égal à une constante, il est souvent d'usage
d'écrire cette dernière égalité sous la forme condensée (et en
mettant la masse dans la constante en question):
 (47.9)
(47.9)
Par ailleurs, rappelons que nous avions aussi obtenu comme résultat
que le mouvement soit et reste plan sans aucune action extérieure!
Nous constatons par ailleurs
que cette loi nous donne que la vitesse de la planète est
variable. Elle est plus grande au périhélie qu'à l'aphélie:

Figure: 47.1 - Représentation des surfaces balayées
Ceci se vérifie pour la
Terre par exemple. En effet, cette dernière est plus proche
du Soleil en hiver (pour l'hémisphère Nord) et
elle a alors une vitesse sur trajectoire un peu plus élevée
qu'en été; le temps
de parcours est donc plus faible (l'hiver compte moins de jours
que les autres saisons).
Enfin remarquons que dans le cas particulier d'une orbite elliptique,
nous avons (voir le démonstration du calcul de l'aire d'une ellipse
dans le chapitre Forme Géométriques):
TROISIÈME
LOI
La "troisième
loi de Kepler", appelée parfois aussi "loi
des périodes", s'énonce
ainsi: Les carrés des périodes de révolution T sont
proportionnels aux cubes des demi-grands axes D des
orbites:
 (47.10)
(47.10)
À nouveau,
nous verrons plus loin que le statut de "loi" n'est
plus justifiable
à notre époque puisqu'il est possible de démontrer
que cette relation, dont l'expression sera détaillée,
est réellement:
 (47.11)
(47.11)
Bien évidemment, Kepler
n'a pas d'emblée
publié ses trois lois dans cette provocante simplicité. Leur
ordre actuel n'est d'ailleurs pas celui de leur énonciation... Elles
sont en réalité à dénicher au milieu d'un foisonnement de spéculations
physiques et de réflexions sur l'harmonie du monde.
LOI
DE LA GRAVITATION DE NEWTON
Pour vérifier l'exactitude
de son hypothèse, Newton (relativement longtemps après) retrouva
les lois de Kepler à partir de la loi de la gravitation, donnant
ainsi l'explication du mouvement général des planètes.
Newton considéra pour déterminer
la loi de gravitation une planète théorique, gravitant autour
du Soleil sur une orbite circulaire à vitesse constante v.
Pendant une orbite complète, la planète parcourt une distance égale à la
circonférence du cercle de rayon R, soit  ,
en un temps (sa période) égal à cette distance divisée par sa
vitesse, soit: ,
en un temps (sa période) égal à cette distance divisée par sa
vitesse, soit:
 (47.12)
(47.12)
Newton s'appuie ensuite
sur la troisième loi de Kepler avec toujours l'hypothèse d'une
orbite circulaire.
Nous avons donc:
 (47.13)
(47.13)
mais puisque:
 (47.14)
(47.14)
alors:
 (47.15)
(47.15)
En comparant:
 (47.16)
(47.16)
et:
 (47.17)
(47.17)
et en posant maintenant que  divisé par
la constante est une nouvelle constante (que nous noterons de
la même manière que la première bien qu'elle
ne lui soit pas égale) on obtient: divisé par
la constante est une nouvelle constante (que nous noterons de
la même manière que la première bien qu'elle
ne lui soit pas égale) on obtient:
 (47.18)
(47.18)
d'où:
 (47.19)
(47.19)
Ensuite, si nous renversons
les termes, cette expression devient (tout en notant que l'inverse
de la constante d'origine est, elle aussi, une constante):
 (47.20)
(47.20)
Par un autre calcul, nous
avons déjà établi dans le chapitre de Mécanique
Classique l'expression de la force centrifuge:
 (47.21)
(47.21)
en rapprochant cette expression de l'expression
précédente:
 (47.22)
(47.22)
nous
obtenons:
 (47.23)
(47.23)
Il existerait donc une force
opposée à la force centrifuge qui maintient la cohésion orbitale
et qui s'écrit:
 (47.24)
(47.24)
reste à déterminer la valeur
de la constante!
Il est trivial que la masse
centrale M du système orbital doit intervenir d'une façon
ou d'une autre dans cette constante. Si la masse du corps secondaire
intervient de façon proportionnelle dans la force centrifuge,
l'envie est grande de faire de même avec la masse du corps central.
Donc:
 (47.25)
(47.25)
maintenant a priori il n'y
aurait plus de paramètres à prendre en compte. La constante restante
est là pour satisfaire à l'analyse dimensionnelle de telle façon
que l'on ait des "Newtons" (nom donné à l'unité de
force) des deux côtés de l'égalité. Les
scientifiques ont déterminé avec grande précision cette "constante
gravitationnelle" notée G qui a priori semble
universelle et qui a comme valeur:
 (47.26)
(47.26)
Ce qui nous amène à écrire
la "loi de la gravitation de Newton":
 (47.27)
(47.27)
Évidemment il ne s'agit
nullement d'une vraie démonstration car nous nous sommes
basés
sur les observations expérimentales de Kepler. Par contre, à partir
de la relativité générale il est possible
de la démontrer (sous certaines hypothèses...)!
En utilisant Maple 17.00, nous pouvons simuler la trajectoire
plane d'un satellite par rapport à un nombre n de
masses fixes (merci à Forhad Ahmed pour ce script)
. Voici par exemple le code de base que vous pouvez
personnaliser selon vos goûts et n'hésitez pas à nous
communiquer votre travail
personnel si vous avez amené une amélioration significative à
ce script:
>restart; with(plots); with(DEtools)
>G:=1; #constante gravitationelle abusivement normalisée pour simplifier...
>poles:=2; #nombre de corps adaptable à loisir...
>M[1]:=10;M[2]:=1; #masse du premier et deuxième corps (en
valeurs relatives)
>h[1]:=1;h[2]:=-1; #position X du premier et deuxième corps (en
unités astronomiques)
>k[1] := 1;k[2] := 1; #position Y du premier et deuxième
corps (en
unités astronomiques)
>#équation différentielle de l'accélération du satellite en
X
>Xeq := diff(x(t), t, t) = sum(-G*M[j]*(x(t)-h[j])/((x(t)-h[j])^2+(y(t)-k[j])^2)^(3/2),
j = 1 .. poles);
>#équation différentielle de l'accélération
du satellite en Y
>Yeq := diff(y(t), t, t) = sum(-G*M[j]*(y(t)-k[j])/((x(t)-h[j])^2+(y(t)-k[j])^2)^(3/2),
j = 1 .. poles);
>#position et vitesse initiale respective du satellite
>inits := x(0) = -2, y(0) = 0, (D(x))(0) = 0, (D(y))(0) = 2
>#résolution numérique de l'ED (jouez avec la précision de l'erreur
au besoin!)
>g:=dsolve({Xeq,Yeq,inits},{x(t),y(t)},type=numeric,method=dverk78,abserr=0.1e-3,
output= procedurelist);
>n:=50; #pas des itérations
>iter:=300; #nombre d'itérations
>#boucle qui résout l'E.D. à chaque nouvelle position
>for i from 0 to iter do
px[i]:=rhs(g(i/n)[2]);
py[i]:=rhs(g(i/n)[4]);
KE[i]:=1/2*(rhs(g(i/n)[3])^2+rhs(g(i/n)[5])^2);
temp:=(rhs(g(i/n)[2])-h[j])^2+(rhs(g(i/n)[4])-k[j])^2;
PE[i]:=sum(-G*M[j]/sqrt(temp), j = 1 .. poles);
TE[i]:=KE[i]+PE[i]
end
do:
>data:=seq(pointplot([px[i], py[i]], color = red), i = 0 ..
iter):
>#mettre insequence à true pour avoir une animation
>Anim:=display(data,insequence=false,scaling=constrained,axes=boxed):
>stars:=display(seq(pointplot([h[i], k[i]], color = black), i =
1 .. poles))
>isplay({Anim,stars},title=`Satellite orbiting a multipolar gravity
field`);

Figure: 47.2 - Trajectoire d'un corps dans le plan influencé par deux corps massifs
et.... statiques...
>#on vérifie que l'énergie totale du satellite est toujours constante
>print(`[Time] -- [Kinetic Energy] - [Potential Energy]
- [Net Energy]`);
>print(`======================================`);
>
for i by 3
to iter do
print(evalf(i/n, 6), ` `, KE[i], ` `, PE[i], ` `,
TE[i]);
end do:
>#la dernière colonne du tableau doit avoir toujours une valeur
égale normalement...
Remarque: En
égalisant force centrifuge et force gravitationnelle, il
est assez facile d'obtenir une approximation de la vitesse de rotation
des
planètes sur leur orbite. Le lecteur qui fera le calcul
verra que le chiffre tourne pour les planètes du système
solaire autour d'une vitesse de l'ordre de 100'000 [km/h].
À partir de cette dernière
relation, revenons brièvement sur notre troisième
loi de Kepler et détaillons là un peu pour montrer
qu'elle est valable pour tout type d'orbite conique et afin de
déterminer l'expression de sa constante.
Exprimée dans le
repère de Frenet (cf. chapitre de
Géométrie
Différentielle), et décomposée en
son accélération normale (centripète) et
tangentielle, l'accélération par rapport à un
référentiel géocentrique (dans le cas d'un
référentiel situé au centre de masse du
système l'expression change un peu) s'écrit:
 (47.28)
(47.28)
Des relations
obtenues lors des développements précédents:
 (47.29)
(47.29)
et:
 (47.30)
(47.30)
la constante de la troisième
loi de Kepler prend comme valeur (c'est une formulation utilisée
parfois dans la pratique mais une étape non rigoureusement
nécessaire dans le présent développement):
 (47.31)
(47.31)
Or, puisque nous avons aussi:
 (47.32)
(47.32)
alors:
 (47.33)
(47.33)
d'où:
 (47.34)
(47.34)
Finalement,
la troisième loi de Kepler se retrouve alors fréquemment
dans la littérature sous la forme suivante:
 (47.35)
(47.35)
Cet interlude effectué,
revenons sur notre loi de la gravitation de Newton:
 (47.36)
(47.36)
À partir de cette loi de
la gravitation, nous pouvons retrouver toutes les lois de Kepler.
D'ailleurs, nous l'avons déjà fait pour la deuxième
et troisième
loi de Kepler puisque ce sont ces dernières que nous avons
utilisées pour
obtenir cette relation (c'est cependant un peu le serpent qui
se mange la queue...).
Sous forme vectorielle nous
avons ainsi:
 (47.37)
(47.37)
Identiquement au champ électrique
(cf. chapitre d'Électrostatique),
nous pouvons développer:
 (47.38)
(47.38)
Comme le champ électrique
dérive d'un potentiel électrique, identiquement, le champ gravitationnel
dérive lui aussi d'un potentiel gravitationnel. En effectuant
le même développement qu'en électromagnétisme pour la première équation
de Maxwell (cf. chapitre d'Électrodynamique),
nous démontrons que:
 (47.39)
(47.39)
où  est
le "potentiel gravitationnel"
qui varie en raison inverse de la distance relative des corps
(ceci confirmant ce que nous
avions
démontré lors de notre étude du théorème
de Noether dans le chapitre traitant des Principes)
et vaut donc: est
le "potentiel gravitationnel"
qui varie en raison inverse de la distance relative des corps
(ceci confirmant ce que nous
avions
démontré lors de notre étude du théorème
de Noether dans le chapitre traitant des Principes)
et vaut donc:

Remarque: Nous retrouverons souvent ce potentiel dans
le chapitre de Relativité Générale. Il convient
donc de s'en souvenir si possible.
Écriture qui implique bien évidemment la relation
suivante:
 (47.40)
(47.40)
Remarque: Évidemment en l'absence de champ, nous
avons  et
donc  sera
nul.
Comme en électromagnétisme à nouveau,
nous démontrons comme nous l'avons fait pour la première équation
de Maxwell que:
 (47.41)
(47.41)
Si nous exprimons cette équation
en fonction d'un potentiel gravitationnel  (noté
aussi souvent par la lettre U comme en Électrostatique...), nous
obtenons: (noté
aussi souvent par la lettre U comme en Électrostatique...), nous
obtenons:
 (47.42)
(47.42)
ce que l'on note de façon
plus esthétique avec le laplacien scalaire (cf.
chapitre de Calcul Vectoriel):
 (47.43)
(47.43)
qui n'est autre
que "l'équation de Newton-Poisson" que
nous retrouverons aussi lors de notre étude de la relativité générale
(elle y a une place importante pour des raisons de validation
de la théorie d'Einstein)!
Cette équation signifie que la théorie Newtonienne
de la gravitation se résume à dire que le champ gravitationnel
est décrit par un
seul potentiel  engendré
par la densité volumique de masse et déterminant
l'accélération
d'une particule d'épreuve plongée dans le champ
extérieur engendré
par la densité volumique de masse et déterminant
l'accélération
d'une particule d'épreuve plongée dans le champ
extérieur  . .
Amusons-nous maintenant
un peu avec l'équation de la gravitation de Newton pour
obtenir quelques résultats intéressants et curieux:
Soit un objet situé à l'extérieur de
la Terre et r la distance de cet objet au centre de la Terre, nous
avons:
 (47.44)
(47.44)
il vient:
 (47.45)
(47.45)
Si l'objet est situé à la surface de la Terre
de rayon R, nous avons (r = R):
 (47.46)
(47.46)
Des deux dernières relations
il vient donc:
 (47.47)
(47.47)
En surface nous avons donc
bien (on s'y attendait...):
 (47.48)
(47.48)
Maintenant, si l'objet est situé à l'intérieur
de la Terre en notant la distance par rapport au centre par la
lettre r et
la masse centrale par M ',
nous avons:
 (47.49)
(47.49)
Introduisons la masse volumique  que
nous supposerons égale partout. que
nous supposerons égale partout.
 (47.50)
(47.50)
En combinant ces quatre
dernières relations, nous obtenons:
 (47.51)
(47.51)

Figure: 47.3 - Profil intérieur/extérieur de l'accélération gravitationnelle
Pour de nombreuses
personnes ce résultat est assez contre intuitif (faites
un petit sondage dans votre entourage, vous verrez).
SPHÉRISATION DES CORPS CÉLESTES
À l'aide de la loi de Newton, nous pouvons répondre à pas
mal de questions pertinentes de manière approximative et
nous donnant des résultats tout à fait probants.
Un premier exemple est de se demander à quelle échelle
il y a une transition du domaine des formes (les astéroïdes,
lunes de Mars, comètes, etc.) au domaine des sphères
(planètes et grandes
lunes)? Pourquoi les satellites de Mars, Phobos et Deimos, ont
une forme patatoïde tandis que notre lune est à peu près
sphérique.
Nous allons voir que ceci est dû à la masse qui est plus
importante dans le cas de notre lune. Effectivement, à partir
d'une certaine masse, les formes géométriques quelconques
ne sont plus possibles.
Pour aborder cette étude, nous allons d'abord estimer
la hauteur maximale d'une montagne sur une planète. Le Mont
Everest a une altitude de 8.8 [km] tandis que le Mont Olympus
sur Mars est de 27 [km]. Pourquoi de telles montagnes ne
peuvent-elles exister sur Terre?
Pour prendre une approche simpliste, nous allons supposer qu'une
montagne doit être en équilibre hydrostatique. Nous connaissons
expérimentalement la pression limite type dans un réseau
cristallin de roches au-delà de laquelle les roches commencent à "couler":  . .
Nous connaissons de par notre étude la mécanique
des milieux continus (cf. chapitre de Mécanique
Des Milieux Continus) que la
pression à la
base d'une montagne de hauteur h sera donnée dans
l'approximation hydrostatique par:
 (47.52)
(47.52)
Pour que la montagne soit stable, il faut donc que:
 et
donc et
donc  (47.53)
(47.53)
Ainsi:
 (47.54)
(47.54)
En supposant une densité moyenne de  (croûte
continentale de la Terre) nous obtenons: (croûte
continentale de la Terre) nous obtenons:
- Terre: 
- Mars: 
Ce qui est remarquable comme résultat approximatif...
Pour estimer la taille minimale  d'un
astre, à partir de laquelle la forme sphérique devient
prédominante
par rapport aux déformations de la surface (c'est-à-dire
où la
gravitation a pris le dessus sur les forces interatomiques), nous
allons exiger que la taille d'un
astre, à partir de laquelle la forme sphérique devient
prédominante
par rapport aux déformations de la surface (c'est-à-dire
où la
gravitation a pris le dessus sur les forces interatomiques), nous
allons exiger que la taille  soit
supérieure à la hauteur maximale d'une montagne soit
supérieure à la hauteur maximale d'une montagne  .
Nous supposons aussi que la densité .
Nous supposons aussi que la densité  reste
constante à travers l'astre. En reprenant la relation: reste
constante à travers l'astre. En reprenant la relation:
 (47.55)
(47.55)
nous avons:
 (47.56)
(47.56)
d'où:
 (47.57)
(47.57)
La limite  peut
ensuite être estimée en fixant peut
ensuite être estimée en fixant  ainsi: ainsi:
 (47.58)
(47.58)
bien évidemment pour  nous
serons encore plus proche de la forme sphérique. nous
serons encore plus proche de la forme sphérique.
APLATISSEMENT DES CORPS CÉLESTES
À cause de la symétrie du potentiel gravitationnel
une étoile
ou une planète devrait avoir une forme parfaitement sphérique à partir
d'une certaine taille comme
nous venons de le voir. Or, il n'en n'est pas ainsi.
À cause de la rotation propre de l'astre, un terme centrifuge
vient modifier le potentiel. Ce terme dépend de la latitude
ce qui explique la forme ellipsoïdale.
Rappelons que:
 (47.59)
(47.59)
où R est le rayon équatorial de l'astre à laquelle vient
s'ajouter l'accélération centrifuge à une latitude donnée de rayon r:
 (47.60)
(47.60)
Ainsi, l'accélération totale:
 (47.61)
(47.61)
explique simplement que la Terre est aplatie aux pôles (ou selon
le point de vue: étirée à l'équateur...) et que plus une planète
tourne vide, plus elle sera aplatie aux pôles.
Sur Terre, le rayon équatorial est de 6379 [km] tandis
que le rayon polaire est de 6357 [km]. La différence est
de 22 [km]. "L'aplatissement"
d'une planète peut être exprimé comme:
 (47.62)
(47.62)
soit la différence entre rayon équatorial et le
rayon polaire divisée par le rayon équatorial.
Bien qu'un ellipsoïde de révolution soit la meilleure description
pour la forme d'une planète:

Figure: 47.4 - Image de la Terre avec son atmosphère
il y a des imperfections entre le modèle et la réalité pour
certains corps du système solaire (en particulier les planètes
telluriques, les satellites, et les petits corps rocheux). Le géopotentiel
d'une planète réelle peut avoir une forme nettement
plus compliquée à cause
des influences des inhomogénéités visibles
à la surface comme l'atteste cette image satellite de la Terre
omettant les parties
liquides (les déformations ont été un
peu exagérées
sur l'image ci-dessous):

Figure: 47.5 - Image de la Terre sans son atmosphère
Les géodésistes tiennent compte de ces inhomogénéités. Ils mesurent
et décrivent la forme des planètes qu'ils appellent "géoïdes".
STABILITÉ DES ATMOSPHÈRES
En comparant les vitesses de libération et les vitesses
de divers gaz, nous pouvons expliquer la stabilité de certaines
atmosphères
et l'inexistence d'autres. Nous avons démontré dans
le chapitre de Mécanique Classique que la vitesse de libération
d'un astre sphérique était
donnée
par la relation suivante (sur laquelle nous reviendrons aussi
dans le chapitre de Relativité Générale):
 (47.63)
(47.63)
Pour la Terre, une application numérique donne  et
pour la Lune et
pour la Lune  . .
Rappelons que nous avons démontré dans le chapitre
de Mécanique Des Milieux Continus lors de notre détermination
de la température cinétique la relation
suivante:
 (47.64)
(47.64)
En utilisant la masse molaire (cf. chapitre
de Chimie Thermique):
 (47.65)
(47.65)
Une application numérique donne pour l'azote  et
pour l'hydrogène et
pour l'hydrogène  avec
une température arbitraire de 300 [K]. avec
une température arbitraire de 300 [K].
Donc l'azote est nettement piégé dans l'atmosphère
terrestre. L'hydrogène, gaz léger, donc rapide l'est
moins. Les deux gaz sont encore moins retenus par la Lune.
Remarque: En fait, la vitesse quadratique moyenne n'est
pas la vitesse unique des molécules. Il y a une distribution
des vitesses. Nous avons effectivement vu la distribution de
Maxwell-Boltzmann
d'un gaz à l'équilibre dans le chapitre de Mécanique
Statistique.
LIMITE DE ROCHE
La limite de Roche est la distance théorique en dessous
de laquelle un satellite commencerait à se disloquer sous
l'action des forces de marées causées par le corps
céleste autour duquel il orbite,
ces forces dépassant la cohésion interne du satellite.
Nous pouvons simplifier le problème en considérant le satellite
liquide et en le décomposant en deux petites masses m de
rayon r et de masse volumique  . .

Figure: 47.6 - Configuration pour l'étude de la limite de Roche
La planète est une sphère de rayon R, de
masse M,
de masse volumique  ,
située à une distance D de l'axe du satellite. ,
située à une distance D de l'axe du satellite.
La planète exerce sur le satellite une attraction gravitationnelle:
 (47.66)
(47.66)
La différence de force entre les 2 masses est:
 (47.67)
(47.67)
Nous pouvons considérer  ,
ce qui donne: ,
ce qui donne:
 (47.68)
(47.68)
Donc la différence de force est
 (47.69)
(47.69)
La force de cohésion du satellite résulte dans l'attraction gravitationnelle
entre les 2 masses:
 (47.70)
(47.70)
Le satellite est détruit si la différence de force entre les 2
masses est supérieure à la force de cohésion
 (47.71)
(47.71)
Or nous avons les relations:
 et et  (47.72)
(47.72)
donc nous obtenons:
 (47.73)
(47.73)
et nous en déduisons la "limite de
Roche":
 (47.74)
(47.74)
Comme, dans ce calcul, nous avons considéré un
satellite constitué de deux masses ponctuelles, et que de
plus nous avons supposé que la cohésion
du satellite était
assurée exclusivement par les interactions gravitationnelles,
cette valeur n'est qu'un ordre de grandeur (un minimum donc!).
Il faut savoir que les forces de marées de
Jupiter ou de Saturne sur leurs satellites respectifs déforment
de plusieurs centaines de mètres leur structure interne.
Cela a pour effet de dégager
de la chaleur par friction et déformation et provoque une
dynamique de surface (éruptions) qui peut aider à l'émergence
d'une forme de la vie élémentaire
même dans les conditions extrêmes de température
qui y règnent.
TRAJECTOIRES D'ORBITALES KÉPLÉRIENNES
L'observation
(outil principal du physicien pour rappel) semble montrer qu'à première
vue, les trajectoires suivies par les corps célestes
en orbite autour d'astres sont bien du type conique (ouf!).
Sachant cela, nous pouvons, afin de faciliter les calculs, anticiper
la complexification
des calculs et exprimer directement la dynamique d'un point matériel
en des coordonnées polaires.
Comme nous l'avons vu dans
le chapitre de Calcul Vectoriel, la vitesse en coordonnées
polaires s'exprime par la relation (nous avons changé la lettre
grecque de notation de l'angle pour nous adapter à la tradition):
 (47.75)
(47.75)
où pour rappel le premier
terme est la composante radiale de la vitesse et le second la
composante
tangentielle de
la vitesse (angulaire).
Pour l'accélération (la démonstration se
trouvant toujours dans le chapitre de Calcul Vectoriel):
 (47.76)
(47.76)
Maintenant que nous avons les outils
nécessaires, attaquons-nous au cas des orbites Képlériennes
dans le cas d'un champ Newtonien.
Il existe à notre connaissance
deux manières principales de faire les développements
mathématiques nécessaires
mais qui n'amènent pas (à notre connaissance) au
même niveau de
détail quant au résultat. La première approche
qui permet d'obtenir un résultat
plus fin mais où la démarche est un peu du bricolage
par moments... est basée sur l'utilisation de la vitesse
radiale et d'une relation importante en astronomie, appelée "première
formule de Binet". La seconde
approche est la plus simple et la plus élégante,
elle utilise l'accélération radiale pour l'approche
du problème et une relation spéciale appelée "deuxième
formule de Binet".
PREMIÈRE FORMULE DE BINET
Pour commencer par cette première approche du problème,
rappelons que nous avons déjà démontré plus haut que:
 (47.77)
(47.77)
Cependant,
il est peu probable que le corps principal soit une sphère
parfaite et homogène... Les astrophysiciens ont donc l'habitude
de noter le potentiel Newtonien U sous la forme:
 (47.78)
(47.78)
où  est
appelée "constante de gravitation de
l'astre" et où f est
une fonction représentant les hétérogénéités de l'astre. est
appelée "constante de gravitation de
l'astre" et où f est
une fonction représentant les hétérogénéités de l'astre.
S'il
est un endroit de l'Univers où les lois de la mécanique
sont parfaitement vérifiables, c'est bien l'espace, parce
que le frottement ou les causes de dissipation y sont extrêmement
faibles. Dans le champ d'une seule force dérivant d'un
potentiel, le mouvement vérifie
la conservation de l'énergie mécanique.
Nous
aboutissons ainsi
à l'équation dite de l'énergie, dans laquelle E désigne "l'énergie
spécifique"
par unité de masse (kilogramme) envoyé.
 (47.79)
(47.79)
donc:
 (47.80)
(47.80)
La
force de gravitation Newtonienne est centrale, donc de couple
nul
au centre O du corps principal. Il en résulte
la conservation du moment cinétique en norme et en direction,
soit:
 (47.81)
(47.81)
Le
vecteur  est
l'unitaire de est
l'unitaire de  ou
de ou
de  appelé
"moment cinétique réduit". K est
la constante des aires (cf. chapitre de
Mécanique Classique) telle
que: appelé
"moment cinétique réduit". K est
la constante des aires (cf. chapitre de
Mécanique Classique) telle
que:
 (47.82)
(47.82)
Nous
rappelons que la norme de la vitesse exprimée en coordonnées
polaires plane est donnée par la relation (n'oubliez pas
que les deux vecteurs de la base polaire sont orthogonaux et que
l'on peut donc
appliquer le théorème de Pythagore pour calculer
la norme comme il l'a été démontré dans
le chapitre de Calcul Vectoriel du site):
 (47.83)
(47.83)
Ce qui nous permet d'écrire pour la constante des aires K:
 (47.84)
(47.84)
Plaçons-nous dans le plan orbital,
en coordonnées polaires. Nous possédons
deux intégrales premières dépendant des deux constantes essentielles
E
et K.
Soit
la relation déjà démontrée:
 (47.85)
(47.85)
et
sa norme au carré:
 (47.86)
(47.86)
Or dans le cas d'une force centrale (conservation du moment cinétique):
 (47.87)
(47.87)
Mettons cela dans l'expression de  antéprécédente,
nous avons alors: antéprécédente,
nous avons alors:
 (47.88)
(47.88)
Cette dernière relation est appelée "première
formule de Binet".
En égalant avec l'expression de  résultant
de la conservation de l'énergie vue un peu plus haut, nous
avons: résultant
de la conservation de l'énergie vue un peu plus haut, nous
avons:
 (47.89)
(47.89)
Ce qui nous donne une équation différentielle
assez compliquée:
 (47.90)
(47.90)
Et là nous nous demandons
comment nous pouvons faire pour nous en sortir? Après quelques
heures de réflexion... nous nous rendons compte qu'il
faut faire une substitution. Après une autre heure de chaos
neuronal cela finit par aboutir. Nous décidons de poser
(nous en avons tout à fait
le droit), sachant que r est
une fonction u de  : :
 (47.91)
(47.91)
Dérivons allègrement par rapport à
 : :
 (47.92)
(47.92)
Substituons dans l'équation différentielle:
 (47.93)
(47.93)
Après simplification, nous obtenons:
 (47.94)
(47.94)
Nous séparons les variables pour intégrer:
 (47.95)
(47.95)
Nous avons deux solutions suivant le
signe que nous choisissons. Cependant, à la fin de la résolution,
nous remarquons que le seul choix physiquement intéressant
est le signe négatif. Nous avons démontré dans le chapitre
de Calcul Différentiel Et Intégral lors de notre étude des dérivées
usuelles que:
 (47.96)
(47.96)
Nous allons opter pour la primitive en cosinus et dès lors,
nous avons:
 (47.97)
(47.97)
Nous laissons, par approximation, de
côté la constante d'intégration qui impliquerait des très faibles
oscillations sur la trajectoire de l'orbite (si vous faites une
étude ou un TP sur le sujet, communiquez-moi les graphiques que
vous obtenez avec ou sans la constante, cela m'intéresserait).
Ce qui nous permet d'obtenir:
 (47.98)
(47.98)
Or, nous voyons que notre choix du
signe pour l'intégration se justifie pleinement puisque
maintenant, si nous faisons un petit rappel sur les coniques (cf.
chapitre de Géométrique Analytique), nous
voyons après réarrangement que nous avons une relation
de la forme:
 (47.99)
(47.99)
où e est l'excentricité
(rapport du petit axe  )
et p le paramètre focal ( )
et p le paramètre focal ( )
d'une ellipse. Ce qui correspond bien aux trajectoires que suivent
les astres en orbite. )
d'une ellipse. Ce qui correspond bien aux trajectoires que suivent
les astres en orbite.
Nous retrouvons donc bien
la première "loi" de Kepler...
Dans notre cas, nous avons après simplification:
 et et
 (47.100)
(47.100)
où (pour rappel) K est la constante
des aires:
 (47.101)
(47.101)
et  la constante
de gravitation de l'astre: la constante
de gravitation de l'astre:
 (47.102)
(47.102)
et enfin E l'énergie spécifique:
 (47.103)
(47.103)
Le lecteur vérifiera comme nous
l'avons vu dans le chapitre de Géométrie Analytique
lors de notre
étude des coniques que si:
-  nous
avons une orbite ouverte sous forme de parabole nous
avons une orbite ouverte sous forme de parabole
-  nous
avons une
orbite ouverte sous forme d'hyperbole nous
avons une
orbite ouverte sous forme d'hyperbole
-  nous
avons une orbite fermée sous forme d'une ellipse ou de
cercle. nous
avons une orbite fermée sous forme d'une ellipse ou de
cercle.

Figure: 47.7 - Rappels sur les coniques
Enfin, si nous injectons:
 (47.104)
(47.104)
dans la première formule de Binet:
 (47.105)
(47.105)
nous obtenons alors la vitesse en n'importe quel
point de l'ellipse en fonction du principal paramètre
variable qui est donc l'angle.
DEUXIÈME FORMULE DE BINET
Voyons maintenant l'approche basée sur l'accélération
radiale qui tout en étant plus élégante, nous
permet d'obtenir un résultat
moins fin concernant les paramètres de l'ellipse.
Nous partons donc l'expression de l'accélération en coordonnées
polaires (cf. chapitre de Calcul Vectoriel):
 (47.106)
(47.106)
Nous pouvons simplifier l'écriture du deuxième terme:
 (47.107)
(47.107)
Or, nous venons de voir plus haut que:
 (47.108)
(47.108)
et donc:
 (47.109)
(47.109)
L'accélération se réduit alors à:
 (47.110)
(47.110)
Nous pouvons éliminer le temps en écrivant:
 (47.111)
(47.111)
et:
 (47.112)
(47.112)
Alors nous obtenons:
 (47.113)
(47.113)
Et donc il vient pour la norme la "deuxième
formule de Binet":
 (47.114)
(47.114)
Or, selon la deuxième loi de Newton et de sa loi
de Gravitation, nous avons:
 (47.115)
(47.115)
Nous avons alors avec la deuxième formule de Binet:
 (47.116)
(47.116)
Soit après simplification et en choisissant
le signe de l'accélération à notre convenance pour se débarrasser
du signe "-", nous avons:
 (47.117)
(47.117)
En isolant les constantes, il vient:
 (47.118)
(47.118)
Après un petit changement de variables
nous reconnaissons le cas particulier d'une équation différentielle
du second ordre que nous avons déjà rencontrée plusieurs
fois jusqu'à maintenant
dans les différents chapitres du site et que nous rencontrerons
encore:
 (47.119)
(47.119)
Comme il est d'usage, nous montrons toutefois les
détails de sa résolution. L'équation sans
second membre est (cf. chapitre de Calcul
Différentiel Et Intégral):
 (47.120)
(47.120)
Nous avons alors le discriminant qui est négatif
puisque:
 (47.121)
(47.121)
Nous avons alors vu dans le chapitre de Calcul Différentiel
Et Intégral, que dans cette situation la solution de
l'équation
homogène était
de la forme:
 (47.122)
(47.122)
Soit dans la situation qui nous concerne, nous avons:
 (47.123)
(47.123)
Nous injectons la solution homogène dans l'équation
différentielle avec second membre:
 (47.124)
(47.124)
Et voyons immédiatement que pour que
l'égalité
soit satisfaite, la solution générale est:
 (47.125)
(47.125)
Soit après réarrangement:
 (47.126)
(47.126)
Et en choisissant l'angle initial comme étant nul,
nous retrouvons donc bien:
 (47.127)
(47.127)
à la différence avec la première
méthode de résolution
que la valeur de la constante A reste inconnue.
Revenons maintenant sur:
 (47.128)
(47.128)
En explicitant:
 (47.129)
(47.129)
Et comme (cf. chapitre de Mécanique
Classique):
 (47.130)
(47.130)
Alors si nous choisissons un point particulier de
référence de la trajectoire (non nécessairement circulaire),
nous aurons:
 (47.131)
(47.131)
Nous avons alors:  (47.132)
(47.132)
Si nous posons le déphasage comme nul par
rapport au rayon de référence choisit plus haut, l'expression se
simplifie en:
 (47.133)
(47.133)
Pour déterminer la constante A, plaçons
dans le cas où  et
qui impose que le rayon r soit le rayon initial mesuré
lorsque cet angle est nul.
Nous avons alors: et
qui impose que le rayon r soit le rayon initial mesuré
lorsque cet angle est nul.
Nous avons alors:
 (47.134)
(47.134)
Ce qui implique immédiatement:
 (47.135)
(47.135)
Soit après réarrangements et simplifications
élémentaires:
 (47.136)
(47.136)
Et dons nous avons une correspondance directe:
 (47.137)
(47.137)
Et comme l'excentricité e est connue pour une trajectoire
circulaire, parabolique, elliptique ou autre... il nous devient
très facile d'en déduire la vitesse de l'objet en question au point
particulier correspondant au rayon initial.
La distance la plus proche de l'objet en orbite de
son astre central (foyer), sera donné par la valeur que prendre r dans
la relation:
 (47.138)
(47.138)
si nous imposons  .
Dans le cas d'une orbite elliptique il s'agit de la "périgée" qui
sera confondu avec le rayon initiale comme étant le point où la
mesure de la vitesse radiale était la plus précise. .
Dans le cas d'une orbite elliptique il s'agit de la "périgée" qui
sera confondu avec le rayon initiale comme étant le point où la
mesure de la vitesse radiale était la plus précise.
La distance la plus éloignée au foyer sera en posant
l'angle comme valant (en degrés) 180° et que nous appelons alors
"l'apogée".
PÉRIODE ORBITALE KÉPLÉRIENNE
La
loi des aires permet, comme nous le savons déjà, de
calculer la période
orbitale Képlérienne
T. En effet, l'aire S de l'ellipse valant  (cf. chapitre sur les Formes Géométriques)
et ayant déjà déterminé lors
de la définition
du moment cinétique
la relation (cf. chapitre de Mécanique
Classique):
(cf. chapitre sur les Formes Géométriques)
et ayant déjà déterminé lors
de la définition
du moment cinétique
la relation (cf. chapitre de Mécanique
Classique):
 (47.139)
(47.139)
Il
vient naturellement:
 (47.140)
(47.140)
Par
ailleurs, l'étude des coniques (cf. chapitre
de Géométrie Analytique)
nous a montré que:
 (47.141) (47.141)
et
nous avons défini plus haut:
 (47.142)
(47.142)
Nous
avons donc la relation:
 (47.143)
(47.143)
et nous retrouvons
du même coup la troisième loi de Kepler...:
 (47.144)
(47.144)
ce qui valide nos calculs précédents.
DÉFLEXION CLASSIQUE DE LA LUMIÈRE
Les calculs effectués
précédemment peuvent s'appliquer à un cas
intéressant: la déviation de la lumière par
un astre selon une interprétation Newtonienne (bien évidemment!).
Attention!!! Newton ne savait pas à l'époque que
le photon était
sans masse. Les développements qui suivent sont donc une
approche erronée à notre époque et qu'il convient
de prendre avec des pincettes mais qui reste enseignée aujourd'hui
car elle permet
à des étudiants
n'ayant pas
encore
étudié
la relativité générale ou qui ne l'étudieront
jamais (dans le chapitre de Relativité Générale,
le lecteur trouvera la démonstration
détaillée contemporaine de la déflexion de
la lumière
qui
est
d'un tout
autre niveau) d'avoir une première approche... C'est comme
dans tout en physique! Tant qu'on n'a pas atteint le niveau de
la licence
universitaire, on apprend plein de choses "fausses" car
simplifiées
à l'extrême. Ensuite au Master et Doctorat, on apprend
des théories
un peu plus réalistes et valides.
Bon ceci étant rappelé (suite
à une remarque d'un lecteur), nous avons donc montré plus
haut que:
 (47.145)
(47.145)
Dans le cas d'un photon,
nous aurions tendance à poser que  (donc une trajectoire de type hyperbolique) et donc pour cela il
faut que dans la relation précédente
nous ayons (ce qui est équivalent à dire que e est
strictement supérieure à l'unité comme l'impose la trajectoire
hyperbolique):
(donc une trajectoire de type hyperbolique) et donc pour cela il
faut que dans la relation précédente
nous ayons (ce qui est équivalent à dire que e est
strictement supérieure à l'unité comme l'impose la trajectoire
hyperbolique):
 (47.146)
(47.146)
en posant  les relations trigonométriques élémentaires
(cf. chapitre de Trigonométrie)
nous donnent:
les relations trigonométriques élémentaires
(cf. chapitre de Trigonométrie)
nous donnent:
 (47.147)
(47.147)
et donc en utilisant encore
les relations trigonométriques:
 (47.148)
(47.148)
soit:
 (47.149)
(47.149)
et nous savons que:
 (47.150)
(47.150)
donc:
 (47.151)
(47.151)
en négligeant l'énergie
potentielle du photon puisque  ,
nous avons (attention!!! rappelons que selon ce que nous avons
vu dans le chapitre de Relativité Restreinte, le photon
n'a pas de masse rigoureusement mais Newton n'en savait rien
à l'époque!): ,
nous avons (attention!!! rappelons que selon ce que nous avons
vu dans le chapitre de Relativité Restreinte, le photon
n'a pas de masse rigoureusement mais Newton n'en savait rien
à l'époque!):
 (47.152)
(47.152)
Donc:
 (47.153)
(47.153)
donc:
 (47.154)
(47.154)
après simplification:
 (47.155)
(47.155)
et comme  est supposé petit, nous avons à l'aide du développement
de Taylor (cf. chapitre sur les Suites Et
Séries) de la fonction tangente:
est supposé petit, nous avons à l'aide du développement
de Taylor (cf. chapitre sur les Suites Et
Séries) de la fonction tangente:
 (47.156)
(47.156)
il vient donc finalement:
 (47.157)
(47.157)
Or, nous avons par définition:
 (47.158)
(47.158)
et nous savons
que  (cf.
chapitre de Mécanique Classique). Ainsi
il vient: (cf.
chapitre de Mécanique Classique). Ainsi
il vient:
 (47.159)
(47.159)
Si la particule est un photon
passant au ras de la surface du Soleil alors:
 (47.160)
(47.160)
une application numérique
donne:
 (47.161)
(47.161)
La théorie Newtonienne prévoit donc une déviation
de 0.87 secondes d'arc pour un rayon lumineux frôlant la
surface
du Soleil. Ce qui est deux fois moins que ce qui peut être
observé
expérimentalement et que ce que donne la relativité générale
(cf. chapitre de Relativité Générale)!
PRÉCESSION DU PÉRIHÉLIE
Avant d'étudier
la précession des orbites, nous souhaiterions rappeler
que le champ gravitationnel est un champ conservatif et central.
Ceci implique
donc que le moment cinétique (cf.
chapitre de Mécanique Classique)
est constant et que la trajectoire a lieu dans un plan dont le
vecteur normal à la surface conserve toujours la même direction
(le vecteur moment cinétique est constant en norme et en
direction pour rappel!).
Nous nous attaquerons
à l'analyse de la précession du périhélie en prenant en compte les
résultats de la théorie de la relativité restreinte (cela permettant
d'être plus fin dans les résultats obtenus
et de pouvoir appliquer ces mêmes résultats aux électrons
en orbite autour du noyau de l'atome).
Définitions:
D1. Le "périhélie"
est le point de l'orbite d'un corps céleste (planète,
comète, etc.) qui est le plus rapproché de l'étoile
autour de laquelle il tourne.
D2. "L'aphélie" est
le point de l'orbite d'un objet (planète, comète,
etc.) où il est
le plus éloigné de l'étoile autour de laquelle
il tourne.
D3. "L'équinoxe"
est l'instant où l'étoile centrale traverse le plan
de l'équateur
de l'objet qui est en orbite autour de lui.
Remarque: Lorsque le Soleil passe de l'hémisphère
Sud à l'hémisphère Nord de la Terre (en d'autres
termes que le Soleil se trouve au Zénith à l'équateur à midi),
c'est l'équinoxe
de printemps (20 ou 21 mars), dans le sens inverse, c'est l'équinoxe
d'automne (22 ou 23 septembre). À ces dates, il y a égalité du
jour et de la nuit sur toute la Terre.
Évidemment, le résultat
que nous obtiendrons ne sera pas complet, puisque comme nous
le savons, il a fallu attendre
le développement de la relativité générale
pour donner avec exactitude la précession du périhélie
de Mercure (nous y reviendrons).
Pour calculer cet effet de précession, nous allons rechercher
l'équivalent
des formules de Binet vues plus haut
sous forme relativiste (nous verrons la forme classique dans le
chapitre de Relativité Générale). Nous procédons
comme suit:
Le lagrangien relativiste
du système
(cf. chapitre de Relativité Restreinte):
 (47.162)
(47.162)
Remarque: Nous soustrayons l'énergie au repos, car
seul nous intéresse ici l'étude de l'énergie
cinétique
et potentielle. L'énergie potentielle est sommée dans
le lagrangien ci-dessus (ce qui n'est pas conforme à l'usage)
mais nous inverserons le signe plus loin lors des développements.
Avec:  (47.163)
(47.163)
et la
masse réduite:
 (47.164)
(47.164)
Remarque: Pour déterminer l'expression de la vitesse
en coordonnées
polaires, nous avons utilisé le résultat de nos calculs
du chapitre de Calcul Vectoriel.
Le moment cinétique:
 (47.165) (47.165)
sous
forme relativiste et appliqué à notre étude s'écrit:  (47.166)
(47.166)
En prenant la norme, nous avons sans
oublier que dans note étude
 et donc
et donc  : :
 (47.167)
(47.167)
et rappelons que nous avons adopté
l'écriture  .
Ce qui nous donne finalement: .
Ce qui nous donne finalement:
 (47.168)
(47.168)
Pour établir l'équivalent relativiste
des formules de Binet:
- nous déduisons de l'expression du moment cinétique:
 (47.169)
(47.169)
- nous recherchons une relation du
type  (puisque
la trajectoire est une conique): (puisque
la trajectoire est une conique):
 (47.170)
(47.170)
Effectivement car rappelons qu'en coordonnées
polaires la vitesse est donnée par l'expression suivante:
 (47.171)
(47.171)
C'est-à-dire que  .
Cette dernière expression permet d'écrire que: .
Cette dernière expression permet d'écrire que:
 (47.172)
(47.172)
- nous cherchons ensuite une relation
 : :
 (47.173)
(47.173)
Soit:
 (47.174)
(47.174)
À partir des équations obtenues précédemment,
nous avons successivement:
 (47.175)
(47.175)
Rappelons que nous avions défini en
relativité restreinte:
 (47.176)
(47.176)
Avec les équations précédentes, cela
nous donne:
 (47.177)
(47.177)
D'autre part:
 (47.178)
(47.178)
En introduisant l'avant-dernière relation
dans cette dernière:
 (47.179)
(47.179)
En posant  et
comme: et
comme:
 (47.180)
(47.180)
L'avant-dernière relation devient avec
cette dernière expression:
 (47.181)
(47.181)
En égalant cette dernière relation
avec celle du lagrangien:
 (47.182)
(47.182)
En dérivant cette dernière relation
par rapport à  : :
 (47.183)
(47.183)
Effectivement, le lagrangien étant
constant au cours du temps (le système est conservatif !), nous
avons donc:
 (47.184)
(47.184)
et également:
 (47.185)
(47.185)
Or, si nous continuons:
 (47.186)
(47.186)
En se référant à:
 (47.187)
(47.187)
Nous obtenons donc:
 (47.188)
(47.188)
Ce qui donne finalement après quelques
simplifications:
 (47.189)
(47.189)
En multipliant cette dernière par  : :
 (47.190)
(47.190)
Dans un potentiel gravitationnel:
 (47.191)
(47.191)
L'équation de Binet en relativité restreinte
est alors:
 (47.192)
(47.192)
Pour rechercher une solution à cette
équation différentielle, nous allons grouper la variable u
dans le membre de gauche:
 (47.193)
(47.193)
Nous posons:
 et
et  (47.194)
(47.194)
L'équation différentielle s'écrit alors:
 (47.195)
(47.195)
Nous posons:
 (47.196)
(47.196)
En prenant la dérivée seconde:
 (47.197)
(47.197)
Nous trouvons alors une simple équation
différentielle dont la solution est bien connue:
 (47.198)
(47.198)
Les solutions sont du type:
 (47.199)
(47.199)
Ce qui s'écrit encore puisque  est
une constante: est
une constante:
 (47.200) (47.200)
avec
 . .
Pour déterminer les constantes  nous
nous plaçons d'abord dans la situation pour laquelle nous
nous plaçons d'abord dans la situation pour laquelle  ,
où r est minimal et donc par définition u
maximal. ,
où r est minimal et donc par définition u
maximal.
Nous dérivons par rapport à  : :
 (47.201)
(47.201)
Donc  ce
qui fait que la relation: ce
qui fait que la relation:
 (47.202)
(47.202)
devient:
 (47.203)
(47.203)
Écrite autrement (en essayant de revenir sur
une notation similaire à celle de l'étude des coniques)
cela donne:
 (47.204)
(47.204)
Et l'intérêt d'écrire cela ainsi est de remarquer
que nous retombons en fin de compte sur l'équation d'une
ellipse avec p étant
le paramètre focal de la conique, paramètre focal
donné par
(cf. chapitre de Géométrie
Analytique):
 (47.205)
(47.205)
où a est le demi-grand
axe de l'ellipse.
Maintenant posons:
 et et
 (47.206)
(47.206)
Au premier passage par le
périhélie
 où: où:
 (47.207)
(47.207)
nous
avons donc:  (47.208)
(47.208)
Au deuxième passage par
le périhélie
 ,
nous avons: ,
nous avons:
 (47.209)
(47.209)
nous
avons donc également:
 (47.210)
(47.210)
La trajectoire est toujours une ellipse
mais l'angle  qui
était nul au départ est devenu qui
était nul au départ est devenu  . .
Soit si nous avons:
 (47.211)
(47.211)
Alors:
 (47.212)
(47.212)
Ce qui nous donne:
 (47.213)
(47.213)
Étant donné que  ,
un développement en série de Taylor (cf.
chapitre sur les Suites Et Séries): ,
un développement en série de Taylor (cf.
chapitre sur les Suites Et Séries):
 (47.214)
(47.214)
En se limitant à l'ordre 2:
 (47.215)
(47.215)
Donc en conclusion, il y a un avancement du périhélie s'effectuant
dans le sens de rotation du satellite. Pour un référentiel situé dans
le plan de rotation du satellite, la trajectoire est toujours
une
ellipse.
Cette avance est de:
 (47.216)
(47.216)
par période. Soit en explicitant le moment cinétique donné
pour rappel par:
 (47.217)
(47.217)
Il vient alors après simplification:
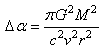 (47.218)
(47.218)
Nous allons maintenant nous permettre une approximation
assez grossière (mélange de relativiste et non relativiste).
Soit à considérer
la dernière relation, nous avons obtenu lors de nos développements
des trajectoires d'orbitales Képlériennes la relation:
 (47.219)
(47.219)
Dès lors en injectant ceci dans la relation de  nous
avons: nous
avons:  (47.220)
(47.220)
Malheureusement, les valeurs numériques pour Mercure ne donnent qu'une
précession de 7'' d'angle par siècle et non pas les 43'' d'angle
par siècle attendus (...) il manque un facteur 6 que seulement la
relativité
générale (cf. chapitre de Relativité Générale)
permet de trouver. Il est néanmoins intéressant de constater que
la relativité, même restreinte, donne déjà une orbite qui précesse
là
où Newton voit une ellipse stable et que cette approximation fonctionne
pour toutes les planètes exceptées Mercure (planète
la plus proche du Soleil et subissant de plein fouet la courbure
de
l'espace-temps).
Remarque: En appliquant exactement le même raisonnement
pour la physique quantique corpusculaire (potentiel électrique)
mais avec les constantes ad hoc vues dans le chapitre d'Électrostatique,
nous trouvons:
 (47.221)
(47.221)
avec  étant
le moment cinétique et dans le cas de l'atome, nous prendrons
(cf.
chapitres Physique Quantique Corpusculaire): étant
le moment cinétique et dans le cas de l'atome, nous prendrons
(cf.
chapitres Physique Quantique Corpusculaire):
 (47.222)
(47.222)
avec la masse réduite valant:
 (47.223)
(47.223)
Si les positions du périhélie (et donc
de l'aphélie) du barycentre Terre-Lune étaient constantes
dans le temps, la durée des différentes saisons
serait, elle aussi constante. Mais l'orbite du barycentre Terre-Lune
tourne elle aussi dans son
plan dans le sens direct à raison d'environ 12'' par an
(soit une révolution en environ 108'000 ans).
La précession des équinoxes
s'effectue dans le sens contraire (sens rétrograde) à raison d'environ
50'' par an (soit une révolution en environ 26'000 ans). La combinaison
de ces deux mouvements permet de calculer la période du passage
du périhélie de la Terre par la direction de l'équinoxe de printemps,
cette période d'environ 21'000 ans est appelée précession climatique.
En effet, tous les 10'500 ans (demi-période de la précession
climatique) l'aphélie passe de l'été à l'hiver.
Or même si la distance Terre-Soleil
n'est de loin pas le facteur prédominant dans la nature
des saisons, la combinaison du passage de la Terre à l'aphélie
en hiver donne des hivers un peu plus rudes. La distance Terre-Soleil
dépend également
de la variation de l'excentricité de l'orbite terrestre
(due aux planètes
extérieures et intérieures). Ainsi, les périodes
glaciaires sont corrélées avec les minima de l'excentricité de
l'orbite terrestre.
Les travaux de l'institut de mécanique
céleste (France), depuis les années 1970, auraient
permis de confirmer définitivement les prédictions
théoriques
comme quoi l'excentricité
de l'orbite terrestre subit de larges variations formées
de nombreux termes périodiques dont les plus importants
ont des périodes voisines
de 100'000 ans, et pour l'un d'eux, une période de 400'000
ans. Ces résultats confirment les variations climatiques
de la Terre au cours de l'ère quaternaire. Les paléoclimatologies
montrent en effet la corrélation entre les variations des éléments
de l'orbite terrestre et les grandes glaciations du quaternaire.
Remarque: Dans le cas de l'atome d'hydrogène (voir le
chapitre de Physique Quantique Corpusculaire traitant du modèle
relativiste de Sommerfeld) avec:

et
la constante de
structure fine égale approximativement à ~1/137,
nous obtenons pour la précession du périhélie de l'orbite donnée:
 (47.224)
(47.224)
selon un point de vue corpusculaire de la matière!
(ce qui nous le savons n'est plus à l'ordre du jour).
DURÉE
DE L'ARC DIURNE
Nous allons nous intéresser à la durée du
jour, plus exactement à la
portion de journée où nous sommes éclairés
par le Soleil, par rapport à la
nuit où nous nous trouvons dans l'ombre.
Remarque: Merci à Xavier Hubaut pour ces très sympathiques
développements.
Dans la réalité, la Terre tourne autour du Soleil
et décrit une
orbite presque circulaire en même temps qu'elle tourne sur elle-même
autour de son axe qui est incliné d'environ 23°27' sur
le plan de son orbite (l'écliptique).

Figure: 47.8 - Représentation de la rotation de la Terre sur son orbite avec
les phases majeures
Remarque: Il est évident qu'étant donnée
la complexité du problème,
nous le simplifierons en considérant une orbite circulaire,
sans variations (précession, nutation) de l'axe de rotation
de la Terre. Nous supposerons que le Soleil se réduit à un
point (pas d'aurore, ni de crépuscule, etc.).
Rappelons que la précession est le changement graduel d'orientation
de l'axe de rotation d'un objet quand un couple (de force) lui
est appliqué alors que la nutation est un balancement périodique
de l'axe de rotation de la Terre autour de sa position moyenne
en plus de la précession.
Représentons la Terre avec son axe de rotation vertical; en conséquence
l'équateur sera situé dans un plan horizontal.
Supposons que ce jour-là, la Terre soit dans une position
telle que les rayons du soleil forment un angle  avec
le plan de l'équateur (ou que réciproquement l'axe
de la Terre forme un angle avec le plan de l'équateur).
Remarquons que cet angle avec
le plan de l'équateur (ou que réciproquement l'axe
de la Terre forme un angle avec le plan de l'équateur).
Remarquons que cet angle  sera
toujours compris selon les mesures actuelles entre -23°27' et +
23°27'. sera
toujours compris selon les mesures actuelles entre -23°27' et +
23°27'.
Pour que les choses soient plus gaies, nous avons choisi de porter
notre analyse sur un jour où  est
positif. Ainsi, dans l'hémisphère nord, nous sommes
proches du solstice d'été! est
positif. Ainsi, dans l'hémisphère nord, nous sommes
proches du solstice d'été!
Nous chercherons donc la durée du jour à un endroit situé à une
latitude  ?
Pour fixer les idées, plaçons-nous dans les environs de
Bruxelles à 50° de
latitude Nord. ?
Pour fixer les idées, plaçons-nous dans les environs de
Bruxelles à 50° de
latitude Nord.
Considérons maintenant les figures ci-dessous où la première
correspond à une vue de la Terre de côté à un
instant t de
son orbite lorsque  et
la seconde à une coupure cylindrique de diamètre NJ (correspondant
au diamètre du parallèle de Bruxelles) du volume
de la Terre à ce
même instant: et
la seconde à une coupure cylindrique de diamètre NJ (correspondant
au diamètre du parallèle de Bruxelles) du volume
de la Terre à ce
même instant:

Figure: 47.9 - Configuration pour l'étude mathématique
Sur les figures ci-dessus, C désigne le centre de la Terre,
et O le centre du parallèle de Bruxelles.
Fixons un instant t et désignons par M (matin)
et S (soir)
les deux points du parallèle de Bruxelles où le Soleil se lève
et se couche (ces points seront considérés comme fixes quel que
soit t pour l'instant,
ce qui est bien évidemment erroné par rapport à la réalité),
tandis que J (jour)
et N (nuit) seront ceux où il est respectivement midi et minuit.
P sera le point sur le disque correspondant à la parallaxe
de Bruxelles où le plan du méridien de midi (le plan dont
un des côtés est NJ) coupe la droite MS.
Enfin,  désignera
l'angle désignera
l'angle  (où O est
donc le centre du disque généré par le parallèle de Bruxelles)
qui sous-tend la partie éclairée par le Soleil et r désignera
le rayon (où O est
donc le centre du disque généré par le parallèle de Bruxelles)
qui sous-tend la partie éclairée par le Soleil et r désignera
le rayon  . .
Pour simplifier le problème, supposons que pendant 24 heures
la Terre tourne sur elle-même sans modifier la position de son
axe de rotation par rapport au Soleil.
L'angle  peut
se calculer en remarquant que OP vaut, en valeur absolue: peut
se calculer en remarquant que OP vaut, en valeur absolue:
 (47.225)
(47.225)
où r représente le rayon du parallèle de Bruxelles.
En utilisant les propriétés des fonctions trigonométriques
(cf. chapitre de Trigonométrie),
nous avons:
 (47.226)
(47.226)
Or, il nous faut encore injecter le paramètre  . Connaissant
la latitude . Connaissant
la latitude  de
Bruxelles, nous avons: de
Bruxelles, nous avons:
 (47.227)
(47.227)
où R est le rayon de la Terre.
Nous avons aussi:
 (47.228)
(47.228)
et dans le triangle COP:
 (47.229)
(47.229)
Enfin, en comparant les valeurs obtenues pour PO, nous
obtenons:
 (47.230)
(47.230)
et comme:
 (47.231)
(47.231)
Nous obtenons finalement:
 (47.232)
(47.232)
et donc:
 (47.233)
(47.233)
Aux équinoxes (c'est-à-dire quand l'équateur est confondu avec
le plan de l'écliptique), nous avons  et
donc: et
donc:
 (47.234)
(47.234)
Or, comme nous l'avons spécifié au début, il faut prendre la
valeur absolue donc:
 (47.235)
(47.235)
En d'autres termes, quelle que soit la latitude que nous prenons,
l'angle formé par la zone de nuit est égal à l'angle
formé par
la zone de jour (les deux étant égaux à  ). ).
Prenons maintenant le solstice d'été, lorsque  en
considérant toujours la latitude de Bruxelles en
considérant toujours la latitude de Bruxelles  ,
nous avons: ,
nous avons:
 (47.236)
(47.236)
ce qui, traduit en nombre d'heures:
 (47.237)
(47.237)
Donc la journée de 24 heures perd 7.9 heures. Ce qui équivaut
donc à une journée d'environ 16 heures.
En résumé pour calculer la durée du jour, il suffit de connaître
deux choses: la latitude du lieu et l'angle selon lequel le soleil
tombe sur le plan de l'équateur à la date choisie. La valeur de
cet angle est bien connue aux équinoxes (il vaut 0°) et aux solstices
(il vaut +23°27' et -23°27').
Mais aux autres dates?
La réponse est fort simple. Imaginons-nous, assis sur le Soleil
regardant tout au long de l'année en direction du centre de la
Terre.
Au cours de sa rotation autour du Soleil, l'axe de rotation de
la Terre conserve son inclinaison sur l'écliptique. Vu du Soleil,
cet axe tournera autour d'une normale au plan de l'écliptique et
décrira donc un cône dont le demi-angle au sommet vaut 23°27' (voir
figure plus bas).
L'angle d'attaque  des
rayons solaires sur le plan de l'équateur variera donc en fonction
de la date des
rayons solaires sur le plan de l'équateur variera donc en fonction
de la date  (nous
associons à la date, l'angle (nous
associons à la date, l'angle  parcouru
par la Terre sur son orbite, à partir de sa position à l'équinoxe
de printemps) parcouru
par la Terre sur son orbite, à partir de sa position à l'équinoxe
de printemps)
Par conséquent, l'angle  variera
en fonction de la date variera
en fonction de la date  de
manière sinusoïdale. de
manière sinusoïdale.
Pour ceux qui ne seraient pas convaincus par ce raisonnement semi-intuitif,
voici une autre approche:
Pour la lisibilité du schéma, nous avons fortement exagéré l'angle
formé par l'axe de rotation de la Terre avec l'écliptique.

Figure: 47.10 - Cône généré par l'axe de rotation de la Terre
(précession)
Soit C le centre de la Terre, A l'extrémité d'un
vecteur unité  dirigé suivant
l'axe de rotation de la Terre (soit perpendiculaire au plan de
l'équateur) et dirigé suivant
l'axe de rotation de la Terre (soit perpendiculaire au plan de
l'équateur) et  un
autre vecteur unité dirigé vers le Soleil. Soit maintenant un
autre vecteur unité dirigé vers le Soleil. Soit maintenant  l'angle
du rayon CS avec le plan de l'équateur et l'angle
du rayon CS avec le plan de l'équateur et  l'angle
entre les vecteurs unitaires l'angle
entre les vecteurs unitaires  et et  .
Nous avons alors: .
Nous avons alors:
 (47.238)
(47.238)
Effectivement, le vecteur  étant
perpendiculaire au plan de l'équateur, il forme un angle
droit avec celui-ci. Dès lors puisque l'angle étant
perpendiculaire au plan de l'équateur, il forme un angle
droit avec celui-ci. Dès lors puisque l'angle  est
l'angle entre ce vecteur et l'écliptique est
l'angle entre ce vecteur et l'écliptique  en
est le complémentaire. en
est le complémentaire.
Nous avons donc:
 (47.239)
(47.239)
Décomposons maintenant  en
la somme de en
la somme de  dirigé perpendiculairement
au plan de l'écliptique et de dirigé perpendiculairement
au plan de l'écliptique et de  situé dans
le plan de l'écliptique: situé dans
le plan de l'écliptique:
 (47.240)
(47.240)
Ainsi:
 (47.241)
(47.241)
Mais:
 (47.242)
(47.242)
Donc finalement:
 (47.243)
(47.243)
et comme nous avons démontré que:
 (47.244)
(47.244)
Nous obtenons finalement:
 (47.245)
(47.245)
À présent le problème est résolu
et la durée du jour sera fonction
de deux variables: la date  et
la latitude et
la latitude  . .
Il nous suffit donc maintenant de reprendre la relation:
 (47.246)
(47.246)
et d'y injecter le nouveau résultat:
 (47.247)
(47.247)
Avec les outils informatiques à notre disposition, nous pouvons
aisément calculer la valeur de  .
Nous avons par exemple ci-dessous les variations de la durée du
jour sur une année à des latitudes allant de 0 à 90° réparties
de 10 en 10° .
Nous avons par exemple ci-dessous les variations de la durée du
jour sur une année à des latitudes allant de 0 à 90° réparties
de 10 en 10°

Figure: 47.11 - Angle de la partie éclairée de la Terre en fonction de la période de
l'année
À partir de la latitude du cercle polaire, nous observons,
en été,
des périodes avec soleil ininterrompu (soleil de minuit)
et, en hiver, des journées entières de nuit.
Pour Bruxelles (latitude=50°)
nous voyons sur le graphique que la durée du
jour varie approximativement entre les valeurs de 16h (solstice d'été) et 8h
(solstice d'hiver).
MOUVEMENTS DES PLANÈTES
Nous allons brièvement nous intéresser aux mouvements des planètes
en situations idéales et simplifiées. Nous ne considérerons que
des mouvements dans le même plan (coplanaires) parfaitement circulaires
et constants.
Définition: Les planètes qui sont plus proches du Soleil
que la Terre (dont le rayon est inférieur à une unité astronomique),
c'est-à-dire les planètes Mercure et Vénus, sont les "planètes
inférieures". Les autres planètes (Mars et au-delà) sont appelées
les "planètes
supérieures".
PÉRIODE SYNODIQUE ET SIDÉRALE
La "période synodique" d'une planète est le temps mis
par cette planète pour revenir à la même configuration Terre-planète-Soleil
(si nous considérons ce cas particulier), c'est-à-dire à la même
place dans le ciel par rapport au Soleil, vu de la Terre. Cette
durée diffère de la période de révolution sidérale de la planète,
car la Terre elle-même se déplace autour du Soleil. En conséquence,
il s'agit de la période de révolution apparente, la durée entre
deux conjonctions planète-Soleil, telle qu'observée depuis la Terre.
Le terme désigne de façon générale le temps séparant deux aspects
identiques de l'objet (opposition, conjonction, quadrature, etc.)
et dépend donc des trois corps impliqués.
Pour étudier mathématiquement le problème en question, considérons
le schéma suivant avec deux planètes décrivant une orbite parfaitement
circulaire à vitesse angulaire constante et dans le même plan et
dans le même sens et où nous avons  (donc
la planète intérieure va plus vite que la planète extérieure): (donc
la planète intérieure va plus vite que la planète extérieure):

Figure: 47.12 - Schéma de base pour la détermination de la période synodique
où  et et  sont
deux planètes quelconques dont nous noterons les périodes sidérales
respectives par sont
deux planètes quelconques dont nous noterons les périodes sidérales
respectives par  et
dont nous déduisons les vitesses angulaires: et
dont nous déduisons les vitesses angulaires:
 (47.248)
(47.248)
Si nous prenons comme temps zéro, le temps où les deux planètes
sont toutes deux alignées sur l'axe X et du même côté de
l'axe (donc en conjonction inférieure), alors l'angle formé entre
ce même
axe et chacune des planètes est:
 (47.249)
(47.249)
Nous avons respectivement:
 (47.250)
(47.250)
Nous cherchons donc tous les instants t où la relation
suivante est satisfaite pour un  fixé: fixé:
 (47.251)
(47.251)
Il vient alors:
 (47.252)
(47.252)
Si nous recherchons à partir du temps zéro la première (prochaine)
conjonction (supérieure), cela revient à poser que  et
donc que: et
donc que:
 (47.253)
(47.253)
Si nous recherchons à partir du temps zéro la première (prochaine)
conjection (inférieure), cela revient à poser que  et
donc que: et
donc que:
 (47.254)
(47.254)
Dans le cas où  (typiquement
la Terre et une des planètes extérieures), le même raisonnement
nous amène à: (typiquement
la Terre et une des planètes extérieures), le même raisonnement
nous amène à:
 (47.255)
(47.255)
Voici quelques périodes synodiques et sidérales des planètes du
système solaire:
|
Planète |
Période synodique [j.] |
Période sidérale [j.] |
|
Mercure |
115.878 |
87.969 |
|
Vénus |
583.921 |
224.709 |
|
Mars |
779.964 |
686.960 |
|
Jupiter |
398.861 |
4'335.355 |
|
Saturne |
378.094 |
10'757.737 |
|
Uranus |
369.654 |
30'708.160 |
|
Neptune |
367.486 |
60'224.904 |
À la vue de ce tableau, nous pouvons faire plusieurs constats
empiriques:
1. Pour les planètes intérieures: Plus nous nous approchons du
Soleil, plus la période synodique est courte, en effet dans la
formule établie,
plus T1 est petit plus T diminue.
Ainsi, s'il existait une planète
tournant très près du Soleil, les deux périodes sidérale et synodique
seraient pratiquement égales.
2. Quand nous nous approchons de la Terre, la période augmente.
S'il existait une planète voisine de la Terre, nous aurions alors
T1 voisin de T2 et la
période synodique deviendrait très grande.
3. Pour les planètes extérieures: La période synodique diminue
quand la planète est plus loin de la Terre et tend vers la période
sidérale terrestre de 365 jours. Nous voyons bien pour Neptune,
si on découvrait une planète située encore plus loin sa période
synodique s'approcherait encore plus de 365 jours.
RÉTROGRADATION DES PLANÈTES
La "rétrogradation" ou "mouvement
rétrograde" d'une
planète est un mouvement apparent de cette planète qui donne l'impression
de s'arrêter dans sa course dans le "mouvement direct" pour
repartir en marche arrière. Ce phénomène est la résultante de la
différence entre la vitesse de révolution de la planète et celle
de la Terre autour du Soleil.
L'exemple ci-dessous illustre à peu près ce qu'un observateur
Terrestre (point jaune) peut observer en surveillant mois après
mois, le mouvement apparent de Mars (point cyan):

Figure: 47.13 - Principe de la rétrogradation (source: Wikipédia)
Pour étudier mathématiquement ce phénomène, nous allons considérer
la situation suivante:

Figure: 47.14 - Schéma de base pour l'étude de la rétrogradation
avec deux planètes décrivant une orbite parfaitement circulaire à vitesse
angulaire constante et dans le même plan et dans le même sens et
où nous avons  .
Il est clair que la planète intérieure va dès lors rattraper la
planète extérieure et elle va sembler avoir un mouvement rétrograde
comme le montre la figure ci-dessous: .
Il est clair que la planète intérieure va dès lors rattraper la
planète extérieure et elle va sembler avoir un mouvement rétrograde
comme le montre la figure ci-dessous:

Figure: 47.15 - Schéma explicatif pour le choix du temps zéro
Comme le lecteur pourra le vérifier sur la figure ci-dessus nous
observons que le mouvement rétrograde par rapport aux étoiles fixes
commence lorsque l'angle entre les deux planètes est nul et qu'il
finit lorsque l'angle entre les deux planètes passe par un maximum.
Dès lors, dans le schéma antéprécédent, nous avons:
 (47.256)
(47.256)
Donc pour connaître le temps entre le moment où l'angle est nul
entre les deux planètes, passe par un maximum et diminue à nouveau,
il suffit de déterminer quand a lieu la variation de signe de la
fonction précédente. Pour cela, il suffit de chercher quand la
dérivée s'annule:
 (47.257)
(47.257)
En appliquant les règles de dérivation vues dans le chapitre de
Calcul Différentiel Et Intégral, nous avons:
 (47.258)
(47.258)
D'où après simplification:
 (47.259)
(47.259)
Nous développons un peu cela:
 (47.260)
(47.260)
et nous simplifions un premier coup:
 (47.261)
(47.261)
et un deuxième:
 (47.262)
(47.262)
et enfin une troisième:
 (47.263)
(47.263)
et après réarrangement:
 (47.264)
(47.264)
Nous simplifions en utilisant une des relations trigonométriques
remarquables démontrées dans le chapitre de Trigonométrie:
 (47.265)
(47.265)
Les valeurs de t qui satisfont cette relation nous donnent
le changement de signe recherché.
Si  est
la première valeur de t qui vérifie l'équation, nous avons: est
la première valeur de t qui vérifie l'équation, nous avons:
 (47.266)
(47.266)
La valeur suivante de t sera telle que:
 (47.267)
(47.267)
et donc:
 (47.268)
(47.268)
Si nous faisons intervenir les périodes de rotation, nous
avons:
 (47.269)
(47.269)
Pour en revenir à:
 (47.270)
(47.270)
il peut être plus commode de l'écrire sous la forme traditionnelle
suivante:
 (47.271)
(47.271)
Jusqu'à maintenant, nous avons fait uniquement de la géométrie.
Aucune loi de la gravitation n'est intervenue dans les calculs.
Comme les rayons sont inconnus ou mal connus (historiquement parlant
du moins), nous allons utiliser la troisième loi de Kepler (loi
des périodes):
 (47.272)
(47.272)
où pour rappel, D est le demi-grand axe de l'orbite, et
si celle-ci est circulaire, cela devient un simple rayon. Nous
avons donc:
 (47.273)
(47.273)
Dès lors:
 (47.274)
(47.274)
et donc:
 (47.275)
(47.275)
Une application numérique donne pour Mercure avec  et
pour la Terre et
pour la Terre  ,
nous obtenons: ,
nous obtenons:
 (47.276)
(47.276)
Valeur que nous avons représentée sur le schéma ci-dessous:

Figure: 47.16 - Représentation du temps calculé
et donc:

Figure: 47.17 - In extenso le temps calculé multiplié par deux
et nous avons donc:
 (47.277)
(47.277)
puis un nouveau cycle:
 (47.278)
(47.278)
etc. Ce qui donne sous forme schématique:

Figure: 47.18 - Schéma de principe du cycle
VITESSE ORBITALE
Nous avons démontré plus haut l'origine de la loi
de Newton. Pour des planètes considérées donc comme des points
physiques en orbite stable, il y a donc équilibre entre force centrifuge
et force gravitationnelle. Nous avons donc:
 (47.279)
(47.279)
d'où nous déduisons aisément:
 (47.280)
(47.280)
Ce qui est approximativement en bon accord avec les
mesures expérimentales comme le montre la figure ci-dessous:

Figure: 47.19 - Vitesse moyenne orbitale en fonction de la distance au Soleil
POINTS DE LAGRANGE
Un "point de Lagrange" (noté L), ou "point
de libration", est une position de l'espace où les champs
de gravité de deux corps en orbite l'un autour de l'autre, et de
masses substantielles, se combinent de manière à fournir un point
d'équilibre à un troisième corps de masse négligeable, tel que
les positions relatives des trois corps soient fixes.
Nous allons dans les développements qui vont suivre nous attarder
à démontrer au mieux que de tels points sont au nombre de 5 notés
respectivement L1à L5.
Il peut être utile de faire une présentation de ces différents
points et de leurs propriétés avant de passer à la
partie calculatoire. Cela aidant peut-être à la compréhension
du sujet.
Nous allons immédiatement considérer le schéma suivant:

Figure: 47.20 - Représentation des cinq points de Lagrange du système Terre-Soleil
Il existe cinq points de Lagrange:
- L1: Sur la ligne définie par les deux masses,
entre celles-ci (c'est le point le plus facile à interpréter intuitivement:
il s'agit par exemple du point où l'attraction gravitationnelle
du Soleil est compensée par celle de la Terre)
 Exemple: Exemple:
Nous considérons un objet orbitant autour du Soleil, plus près
de celui-ci que la Terre mais sur une même ligne. Cet objet subit
une gravité solaire supérieure à celle de la Terre, et tourne donc
plus rapidement autour du Soleil que ne le fait la Terre. Mais la
gravité terrestre contrecarre en partie celle du Soleil, ce qui
le ralentit. Plus on rapproche l'objet de la Terre, plus cet effet
est important. À un certain point, le point L1, la vitesse
angulaire de l'objet devient exactement égale à celle de la Terre.
- L2: Sur la ligne définie par les deux masses,
au-delà de la plus petite (un peu moins intuitif car correspond
au point où l'action cumulée du soleil et de la Terre viennent
compenser la force centrifuge).
 Exemple: Exemple:
Le principe est similaire au cas précédent, de l'autre côté de
la Terre. L'objet devrait tourner moins vite que la Terre parce
que la gravité solaire y est moindre, mais le champ gravitationnel
supplémentaire dû à la Terre tend à l'accélérer. À un certain point,
le point L2, l'objet tourne exactement à la même vitesse
angulaire que la Terre autour du Soleil.
- L3: Sur la ligne définie par les deux masses,
au-delà de la plus grande (intuitif sur la base de considérations
physiques: il est évident qu'un objet diamètralement opposé à la
Terre par rapport au Soleil aurait la même période de révolution
que la Terre, et donc serait fixe relativement au système Terre-Soleil).
 Exemple: Exemple:
De manière identique au point L2, il existe un point situé
un peu plus loin que l'opposé de la Terre par rapport au Soleil,
où un objet de masse négligeable serait en équilibre.
- L4 et L5: Sur les sommets des deux
triangles équilatéraux dont la base est formée par les deux masses.
 Exemple: Exemple:
Il s'agit d'un subtil équilibre entre la force centripète
exercée
par les deux masses principales et la force centrifuge des masses
considérées aux points intéressés. L4 est
en avance sur la plus petite des masses, dans son orbite autour
de la grande,
et L5 est en retard. Ces deux points sont parfois appelés
"points de Lagrange triangulaires" ou "points Troyens".
Fait remarquable, ces deux derniers points ne dépendent en rien
des masses relatives des deux autres corps comme nous le verrons.
Pour les trois premiers points de Lagrange, la stabilité n'apparaît
que dans le plan perpendiculaire à la ligne occupée par les deux
masses. Par exemple, pour le point L1, si nous déplaçons
un objet perpendiculairement à la ligne entre les deux masses,
les deux forces gravitationnelles vont jouer pour le ramener vers
la position initiale. L'équilibre est stable. En revanche, si nous
le déplaçons vers une des deux masses, alors le champ de celle-ci
va l'emporter sur l'autre et l'objet tendra à se rapprocher encore
plus. L'équilibre est instable. Pour les points L4 et L5,
la stabilité est obtenue grâce aux forces de Coriolis qui agissent
sur les objets s'éloignant du point.
Étant données les questions de stabilité évoquées
plus haut, nous ne trouvons pas d'objet naturel autour des points L1, L2
et L3 dans le système solaire. Cependant, ils représentent
tout de même un intérêt pour les réalisations scientifiques,
car ils permettent des économies de combustible pour le
contrôle d'orbite
et d'attitude. Ceci n'est pas valable pour le point L3,
du fait de son éloignement de la Terre dont la seule application était
que les auteurs de science-fiction et de bande dessinée
aimaient y placer une Anti-Terre d'autant plus utopique que la
masse de
cette planète-jumelle y était bien trop élevée
par rapport à la
théorie énoncée plus haut. En revanche, des
missions spatiales utilisent L1 et L2: c'est
le cas de la sonde SoHO (Solar and Heliospheric Observatory) une
station d'observation
du Soleil située au point L1 ou comme le satellie
WMAP proche du point L2 (les radiations de la Terre y sont relativement
faibles et celles du Soleil attenuées par le Terre qui fait écran).
L4 et L5 étant stables, nous y trouvons
de nombreux corps naturels. Dans le système Jupiter-Soleil, plusieurs
centaines d'astéroïdes, appelés astéroïdes Troyens, s'y agglutinent
(près de 1800 en avril 2005). Nous en comptons quelques-uns dans
les systèmes Neptune-Soleil et Mars-Soleil. Curieusement, il
semblerait que le système Saturne-Soleil ne soit pas en mesure
d'en accumuler,
à cause des perturbations joviennes. Nous trouvons également des
objets à ces points dans le système Saturne-satellites de Saturne: Saturne-Téthys avec Télesto et Calypso aux points L4
et L5, et Saturne-Dioné avec Hélène au point L4
et Pollux au point L5. Dans le système Terre-Soleil, il
n'y a pas d'objet connu de grande taille aux points Troyens,
mais on
y a découvert une légère surabondance de poussière en 1950. De
légers
nuages de poussière sont également présents pour le système Terre-Lune;
cela a fait renoncer à y placer un télescope spatial comme le
projet en avait été envisagé. Le satellite SoHO occupe depuis
1995 le point
L1 à 1.5 million de kilomètres de la Terre. En 2007 le point
L2 sera occupé par le satellite Planck chargé d'étudier
le fond diffus cosmologique à 2.7 [°K].
À strictement parler, ces 5 points existent uniquement
pour deux corps en rotation circulaire l'un autour de l'autre.
Dès
que l'orbite des deux corps est elliptique, ces points ne sont
plus
des points d'équilibre. En pratique, si l'orbite est faiblement
elliptique, comme c'est le cas pour les planètes réelles,
on peut trouver des orbites oscillantes stables ne s'écartant
pas beaucoup des régions correspondant aux points de
Lagrange.
Nous allons donc considérer dans l'espace un système
isolé de
deux corps A et B, de masse  et et  ,
en interaction gravitationnelle. Ces deux corps sont en orbite
circuliare (pour simplifier!) l'un autour de l'autre, à la
manière
d'un système
de deux étoiles
(système binaire) ou d'un système planète-satellite
(Saturne-Titan par exemple). Nous cherchons à déterminer
s'il existe des positions d'équilibre par rapport au système
des deux corps en rotation pour un troisième corps lui aussi
en mouvement circulaire dans le même plan (de masse suffisamment
faible pour ne pas perturber le mouvement du
système
des deux corps principaux). ,
en interaction gravitationnelle. Ces deux corps sont en orbite
circuliare (pour simplifier!) l'un autour de l'autre, à la
manière
d'un système
de deux étoiles
(système binaire) ou d'un système planète-satellite
(Saturne-Titan par exemple). Nous cherchons à déterminer
s'il existe des positions d'équilibre par rapport au système
des deux corps en rotation pour un troisième corps lui aussi
en mouvement circulaire dans le même plan (de masse suffisamment
faible pour ne pas perturber le mouvement du
système
des deux corps principaux).

Figure: 47.21 - Configuration choisie pour l'étude mathématique
Soit O le barycentre (cf. chapitre
de Mécanique Classique)
de ces deux astres. Considérons un repère Galiléen
(en mouvement rectiligne et uniforme donc!) d'origine O.
Par rapport à ce
repère, nous supposerons que l'axe AB tourne à une
vitesse angulaire constante  d'axe
fixe d'axe
fixe  (perpendiculaire à la
page dans la figure ci-dessus et dirigé en direction du
lecteur) et que les distances (perpendiculaire à la
page dans la figure ci-dessus et dirigé en direction du
lecteur) et que les distances  et et  restent également
constantes. restent également
constantes.
Nous savons par notre étude de la mécanique classique que dans
un mouvement circulaire la force centrifuge est donnée par:
 (47.281)
(47.281)
Nous avons donc (équilibre entre forces centrifuge et centripète)
pour assurer l'équilibre:
 et et  (47.282) (47.282)
En simplifiant et en sommant ces deux relations:
 (47.283)
(47.283)
avec dans la suite  . .
Considérons un repère tournant R' lié à nos
astres comme représenté sur la figure ci-dessus:  sera
un vecteur unitaire colinéaire à AB, sera
un vecteur unitaire colinéaire à AB,  un
vecteur unitaire perpendiculaire à un
vecteur unitaire perpendiculaire à  et
dans le plan de rotation des planètes et finalement et
dans le plan de rotation des planètes et finalement  colinéaire à colinéaire à  . .
Nous considérons dans ce repère tournant (avec les astres) un
troisième astre S de masse négligeable m devant  et et  ,
soumis à l'attraction gravitationnelle de A et B. ,
soumis à l'attraction gravitationnelle de A et B.
Maintenant notons  l'accélération
de S par rapport à R', l'accélération
de S par rapport à R',  sa
vitesse et sa
vitesse et  le
vecteur unitaire colinéaire à le
vecteur unitaire colinéaire à  où S '
est le projeté de S dans le plan Oxy, et où S '
est le projeté de S dans le plan Oxy, et  (dans
la figure ci-dessus, nous avons supposé S dans le plan Oxy,
et donc S et S ' sont confondus). (dans
la figure ci-dessus, nous avons supposé S dans le plan Oxy,
et donc S et S ' sont confondus).
S est donc soumis à deux forces, l'une  dirigée
vers A et l'autre dirigée
vers A et l'autre  dirigée
vers B, forces d'intensités respectives: dirigée
vers B, forces d'intensités respectives:
 et et  (47.284)
(47.284)
Dans un repère Galiléen, ces deux forces imposent à S une
accélération donnée par la loi de composition
des accélérations
dans un référentiel circulaire (cf.
chapitre de Mécanique Classique):
 (47.285)
(47.285)
Or, dans notre configuration la pulsation est constante et l'accélération
d'entraînement est nulle puisque nous avons posé R ' comme
référentiel principal. Il vient donc:
 (47.286)
(47.286)
Nous avons également:
 (47.287)
(47.287)
où selon schéma toutes les composantes sont positives. Le calcul
du produit vectoriel donne (cf. chapitre
de Calcul Vectoriel):
 (47.288)
(47.288)
Donc finalement:
 (47.289)
(47.289)
Écrivons plutôt cette relation sous la forme:
 (47.290)
(47.290)
Nous obtenons alors, en projetant sur les trois axes x, y et z, les
dérivées prises par rapport au temps t le système suivant:
 (47.291)
(47.291)
avec:
 et et  (47.292)
(47.292)
pour que les coordonnées  du
point S soient celles d'un point d'équilibre, il
est alors trivial
que dans le référentiel tournant avec les astres A et B que: du
point S soient celles d'un point d'équilibre, il
est alors trivial
que dans le référentiel tournant avec les astres A et B que:
 et et  (47.293)
(47.293)
Nous obtenons alors le système suivant:
 (47.294)
(47.294)
Il vient par ailleurs immédiatement que la troisième équation
a pour seule solution  et
donc finalement le système se réduit à: et
donc finalement le système se réduit à:
 (47.295)
(47.295)
La troisième équation signifie simplement que les
positions d'équilibre
sont dans le plan Oxy (on pouvait s'en douter un peu...).
Les deux autres, nous le verrons, nous amènent à considérer
cinq solutions qui sont nos cinq points de Lagrange L1,
..., L5.
Si nous traçons avec un logiciel ad hoc l'accélération
(respectivement la force) avec les isoclines mises en évidence
(courbes sur lesquelles l'accélération a même
norme) nous obtenons:

Figure: 47.22 - Isoclines du système à deux corps
où nous voyons qu'à faible distance des corps l'énergie potentielle
domine, mais qu'à grande distance potentiel centrifuge prédomine
et la forme de la surface se rapproche de celle d'un paraboloïde.
En demandant au logiciel de ne tracer que les isoclines projetées
sur un plan:

Figure: 47.23 - Projection des isoclines sur le plan
où nous avons mis en évidence les cinq points de Lagrange
et où les astres sont représentés
par des points bleus et le barycentre du système par un
point vert. Les isoclines seraient appelées en astronomie "équipotentielles
des lobes de Roche". Autrement vu:

Figure: 47.24 - Le plot 3D et les isoclines (source: Accromath)
Pour ceux qui souhaitent reproduire ces figures avec MATLAB voici
comment procédér d'abord mathématiquement. De ce que nous avons
obtenu plus haut, nous avons donc explicitement et écrit sous une
forme plus scolaire, la relation suivante:
 (47.296)
(47.296)
Comme le point S est censé être à l'équilibre
le dernier terme s'annule (ses vitesses sont nulles dans le référentiel
tournant!). Il reste alors:
 (47.297)
(47.297)
Nous avons démontré pour rappel dans
le chapitre de Mécanique Classique que:
 (47.298)
(47.298)
Nous avons alors:
 (47.299)
(47.299)
Soit rapporté à l'unité de masse du satellite:
 (47.300)
(47.300)
L'application de cette relation dans MATLAB 2013a donne alors
(désolé c'est un peu long et on peut probablement mieux faire...):
%Nous construisons la grille de plot que nous allons par anticipation
%densifier là où il y a les objets qui nous intéressent
x1=linspace(-7E8,-8E5,150);
x2=linspace(8E5,1.2E8,150);
x3=linspace(1.6E8,7E8,150);
x=x1+x2+x3;
y=linspace(-7E8,7E8,450);
[X,Y]=meshgrid(x,y);
%Les masses et G sont les vraies mais le reste est fictif juste
poure que le graphe soit lisible
f=@(x,y) -(1.3346E20)./(sqrt((x-450).^2+y.^2))-(1.0038E19)./(sqrt((x-449999550).^2+y.^2))
-(6.9E-7.*(x.^2+y.^2));
z=f(X,Y);
%Nous éliminons les valeurs sont
trop grandes en Z pour avoir unrésultat esthétique à regarder
for i=1:450;
for j=1:150;
if (z(i,j)<-0.8E12) %pour faire avec meshc un joli graph limiter
-8E11
z(i,j)=-0.8E12;
end;
end;
end;
contour(X,Y,z,100); mesh(X,Y,z); meshc(X,Y,z);
az = 100; el = 25; view(az, el);
axis([-7E8 7E8 -0.8E9 0.8E9 -8E11 -4E11]);
colorbar; light; camlight('right');
Ce qui donne au final:

Figure: 47.25 - Le plot 3D et les isoclines avec MATLAB 2013a
Le lecteur remarquera qu'il est difficile de deviner intuitivement
cette configuration du potentiel. Dans le référentiel
tournant avec le barycentre des deux corps massifs, le potentiel
résultant
de la combinaison des potentiels gravitationnels et rotationnels
présente 3 extrema L1, L2 et L3 sur
la droite contenant les 2 corps. L'un de ces maxima se situe entre
les 2
corps, ce que l'on attend intuitivement. Les deux autres maxima
se trouvent sur la droite reliant les 2 objets, mais de part et
d'autre ...ce qui est plus surprenant. Ils proviennent au fait
de la contribution au potentiel du référentiel tournant
ce qui peut être difficile à modéliser intuitivement.
POSITIONS D'ÉQUILIBRE DU PREMIER TYPE
Ce que nous entendons par les positions d'équilibre du
premier type sont simplement les solutions situées sur la
droite AB telles
que  ce
qui revient à étudier seulement: ce
qui revient à étudier seulement:
 (47.301)
(47.301)
avec dès lors:
 et et  (47.302)
(47.302)
À cette situation, nous allons considérer trois
sous-cas possibles correspondants respectivement à L1, L2
et L3comme nous allons de suite le voir.
POINT L1 DE LAGRANGE
Dans ce premier sous-cas, nous considérons:
 (47.303)
(47.303)
Ce qui revient aussi à avoir:
 (47.304)
(47.304)
Ce qui nous permet d'écrire:
 (47.305)
(47.305)
sous la forme simplifiée suivante:
 (47.306)
(47.306)
Maintenant pour dire quelque chose sur les solutions possibles
de cette équation dérivons le membre de gauche. Nous obtenons alors:
 (47.307)
(47.307)
Ce terme est strictement croissant de  à à  lorsque x décrit lorsque x décrit  .
Il y a donc une solution unique et un point d'équilibre noté L1
(premier point de Lagrange) entre A et B. .
Il y a donc une solution unique et un point d'équilibre noté L1
(premier point de Lagrange) entre A et B.
Si nous considérons typiquement le cas Soleil-Terre où  et
donc et
donc  alors
en alors
en  nous
avons: nous
avons:
 (47.308)
(47.308)
ce qui est immédiatement négatif. La position d'équilibre
sera donc obtenue pour une valeur positive de x que nous
allons devoir déterminer.
Cette valeur peut être obtenue en considérant un cas limite:
lorsque  tend
vers 0 (correspondant à un astre massif A autour
duquel tourne un astre B de masse beaucoup plus petit), A tend
alors vers O, tend
vers 0 (correspondant à un astre massif A autour
duquel tourne un astre B de masse beaucoup plus petit), A tend
alors vers O,  vers
0 et donc: vers
0 et donc:
 (47.309)
(47.309)
avec  .
Dès lors, dans ce cas limite: .
Dès lors, dans ce cas limite:
 (47.310)
(47.310)
devient en approximation:
 (47.311)
(47.311)
et donc:
 (47.312)
(47.312)
Donc la seule valeur de x satisfaisant cette relation
sera  . .
En d'autres termes, le point d'équilibre cherché L1 ici
entre A et B se rapproche de B soit de l'astre
le moins massif (ce qui correspond bien à la première figure que
nous avons utilisé pour montrer l'emplacement des cinq points de
Lagrange).
De par ce constat nous pouvons
effectuer les calculs suivants:

Figure: 47.26 - Configuration pour déterminer mathématiquement la position du point L1
Nous avons d'après la définition du barycentre:
 (47.313)
(47.313)
Comme notre étude se fait par rapport au barycentre nous avons  et
donc: et
donc:
 (47.314)
(47.314)
De la relation précédente en prenant la norme,
nous avons bien évidemment:
 (47.315)
(47.315)
La distance entre les deux astres A et B demeurant
constante et égalant  nous écrivons: nous écrivons:
 (47.316)
(47.316)
Nous en déduisons trivialement deux relations (la deuxième
étant obtenue par exactement le même raisonnement que la première):
 (47.317)
(47.317)
Mais puisque  nous
pouvons grossièrement écrire la première relation
sous la forme approximative suivante (série de Taylor): nous
pouvons grossièrement écrire la première relation
sous la forme approximative suivante (série de Taylor):
 (47.318)
(47.318)
et puisque:
 (47.319)
(47.319)
nous avons aussi:
 (47.320)
(47.320)
Donc avec  : :
 (47.321)
(47.321)
Selon le cas limite étudié précédemment,
nous pouvons donc supposer L voisin
de B tel qu'abusivement il soit possible d'écrire:
 (47.322)
(47.322)
avec  . .
Soit en utilisant:
 (47.323)
(47.323)
Nous avons alors:
 (47.324)
(47.324)
en négligeant les infiniment petits d'ordre 2.
D'où:
 (47.325)
(47.325)
Maintenant dans la configuration mentionnée l'équilibre est donné par:
 (47.326)
(47.326)
Donc:
 (47.327)
(47.327)
Maintenant la troisième loi de Kepler (cf.
chapitre de Mécanique
Classique) nous donne:
 (47.328)
(47.328)
Soit:
 (47.329)
(47.329)
Après simplification:
 (47.330)
(47.330)
Soit:
 (47.331)
(47.331)
Donc:
 (47.332)
(47.332)
Puisque  est
très supérieur à 1 et en admettant que est
très supérieur à 1 et en admettant que  le
soit aussi nous avons: le
soit aussi nous avons:
 (47.333)
(47.333)
Soit finalement:
 (47.334)
(47.334)
et donc:
 (47.335)
(47.335)
Si nous prenons le A Soleil et B la Terre,
alors:
 (47.336)
(47.336)
Nous trouvons que la distance LB vaut à peu près:
 (47.337)
(47.337)
qui est le point L1 auquel a été placé le
satellite SoHO (puisque ce dernier ne se trouvera ainsi jamais
son champ d'observation masqué par l'ombre de la Terre ou de la
Lune).
Un cas particulier du point L1 à considérer est lorsque  ,
alors ,
alors  , O est
alors le milieu de AB. Nous avons alors: , O est
alors le milieu de AB. Nous avons alors:
 (47.338)
(47.338)
Dès lors:
 (47.339)
(47.339)
devient:
 (47.340)
(47.340)
Parmi les quatre racines évidentes de cette équation
la seule solution acceptable est  pour
satisfaire pour
satisfaire  .
En d'autres termes, le point d'équilibre situé entre
deux astres de même masse n'est autre que le barycentre de ces
deux astres. .
En d'autres termes, le point d'équilibre situé entre
deux astres de même masse n'est autre que le barycentre de ces
deux astres.
POINT L2 DE LAGRANGE
Dans ce deuxième sous-cas, nous considérons:
 (47.341)
(47.341)
Nous cherchons donc les points d'équilibre au-delà de B.
Dès lors nous avons:
 (47.342)
(47.342)
qui devient simplement:
 (47.343)
(47.343)
Le membre de gauche est une fonction strictement croissante
de x de  à à  lorsque x décrit lorsque x décrit  .
Il y a donc une solution unique, et un point d'équilibre
au-delà de B.
Ce point est noté L2. .
Il y a donc une solution unique, et un point d'équilibre
au-delà de B.
Ce point est noté L2.
Cette valeur peut être obtenue en considérant un cas limite:
lorsque  tend
vers 0 (correspondant à un astre massif A autour
duquel tourne un astre B de masse beaucoup plus petite), A tend
alors vers O, tend
vers 0 (correspondant à un astre massif A autour
duquel tourne un astre B de masse beaucoup plus petite), A tend
alors vers O,  vers
0 et donc: vers
0 et donc:
 (47.344)
(47.344)
avec  .
Dès lors, dans ce cas limite: .
Dès lors, dans ce cas limite:
 (47.345) (47.345)
devient en approximation:
 (47.346)
(47.346)
et donc:
 (47.347)
(47.347)
Donc la seule valeur de x satisfaisant cette relation
sera  .
Le point L2 finit donc par se confondre avec B. .
Le point L2 finit donc par se confondre avec B.
Connaissant ce cas limite, faisons une étude plus détaillée.
Considérons le schéma suivant relativement à notre situation limite
précédente:

Figure: 47.27 - Configuration pour déterminer mathématiquement la position
du point L2
et considérons  sans
oublier que dans ce scénario sans
oublier que dans ce scénario 
Nous avons alors quasiment les mêmes développements que pour L1 à la
différence que:
 (47.348)
(47.348)
Devient:
 (47.349)
(47.349)
et que plutôt que d'avoir:
 (47.350)
(47.350)
Nous avons:
 (47.351)
(47.351)
et donc:
 (47.352)
(47.352)
Toujours avec:
 (47.353)
(47.353)
et donc:
 (47.354)
(47.354)
ce qui correspond au point de Lagrange L2.
Un cas particulier à nouveau de L2 est lorsque  ,
alors ,
alors  , O est
alors le milieu de AB. Nous avons alors: , O est
alors le milieu de AB. Nous avons alors:
 (47.355)
(47.355)
Dès lors:
 (47.356)
(47.356)
devient:
 (47.357)
(47.357)
Il n'est plus possible d'extraire les racines ici (du moins à
ma connaissance). Il faut passer par une approximation numérique.
Dans Maple 4.00b,
il suffit de mettre:
>solve(-1/(r+x)^2-1/(x-r)^2=x/(8*r^3),x);allvalues(");
et la seule solution admissible dans  est est  les
autres étant dans les
autres étant dans  . .
POINT L3 DE LAGRANGE
Dans ce troisième sous-cas, nous considérons:
 (47.358)
(47.358)
Nous cherchons donc les points d'équilibre au-delà de A.
Dès lors nous avons:
 (47.359)
(47.359)
qui devient simplement:
 (47.360)
(47.360)
Le membre de gauche est une fonction strictement croissante
de x de  à à  lorsque x décrit lorsque x décrit  .
Il y a donc une solution unique, et un point d'équilibre
au-delà de A.
Ce point est noté L3. .
Il y a donc une solution unique, et un point d'équilibre
au-delà de A.
Ce point est noté L3.
Cette valeur peut être obtenue en considérant un cas limite:
lorsque  tend
vers 0 (correspondant à un astre massif A autour duquel
tourne un astre B de masse beaucoup plus petit), A tend
alors vers O, tend
vers 0 (correspondant à un astre massif A autour duquel
tourne un astre B de masse beaucoup plus petit), A tend
alors vers O,  vers
0 et donc: vers
0 et donc:
 (47.361)
(47.361)
avec  .
Dès lors, dans ce cas limite: .
Dès lors, dans ce cas limite:
 (47.362)
(47.362)
devient en approximation:
 (47.363)
(47.363)
et donc:
 (47.364)
(47.364)
Donc la seule valeur de x satisfaisant cette relation
sera  .
Le point L3 finit donc par se confondre avec la position
diamétralement opposée à B. .
Le point L3 finit donc par se confondre avec la position
diamétralement opposée à B.
Connaissant ce cas limite, faisons une étude plus détaillée.
Considérons le schéma suivant relativement à notre situation limite
précédente:

Figure: 47.28 - Configuration pour déterminer mathématiquement la position
du point L3
et considérons toujours  sans
oublier que dans ce scénario sans
oublier que dans ce scénario 
Nous allons considérer d'abord l'approximation suivante:
 (47.365)
(47.365)
et celle-ci aussi (puisque OA tend vers zéro lorsque l'astre A devient
très massif):
 (47.366)
(47.366)
Dès lors:
 (47.367)
(47.367)
Nous avons aussi (...):
 (47.368)
(47.368)
où à la limite où l'astre A est vraiment massif, nous
retombons sur le premier terme...
Avec ces deux dernières relations, nous avons:
 (47.369)
(47.369)
si nous négligeons les termes du deuxième ordre.
Nous avons par ailleurs aussi:
 (47.370)
(47.370)
Rappelons la condition d'équilibre:
 (47.371)
(47.371)
Et mettons tout ce que nous avons obtenu avant là-dedans:
 (47.372)
(47.372)
Ce qui devient après simplifications:
 (47.373)
(47.373)
après une petite approximation:
 (47.374)
(47.374)
après simplification:
 (47.375)
(47.375)
D'où:
 (47.376)
(47.376)
et finalement:
 (47.377)
(47.377)
Remarque: Chez certains auteurs de science-fiction, ce
point L3
à l'opposé de la Terre par rapport au Soleil nous cacherait une
hypothétique planète qui nous serait perpétuellement cachée par
le Soleil.
POSITIONS D'ÉQUILIBRE DU DEUXIÈME TYPE
Les positions d'équilibre du deuxième type sont donc celles pour
lesquelles  .
En d'autres termes les points situés hors de la droite AB,
mais dans le plan Oxy. .
En d'autres termes les points situés hors de la droite AB,
mais dans le plan Oxy.
Ainsi, notre système d'équations reste:
 (47.378)
(47.378)
POINTS L4, L5 DE LAGRANGE
Pour déterminer les autres points d'équilibre restants,
nous pouvons diviser la deuxième équation du système
par y tel que le
système devienne:
 (47.379)
(47.379)
Retranchons de la première équation la deuxième
multipliée par x.
Nous obtenons alors pour la première:
 (47.380)
(47.380)
Soit:
 (47.381)
(47.381)
Mais comme  ceci
se simplifie encore en: ceci
se simplifie encore en:
 (47.382)
(47.382)
Reprenons maintenant, en toute généralité, notre schéma
du début en rajoutant quelques éléments:

Figure: 47.29 - Configuration pour déterminer mathématiquement la position
des points L4 et L5
où AB est la distance entre A et B et D est
le centre de masse du système donné par:
 ou ou  (47.383)
(47.383)
qui sont donc les rayons de giration des corps A et B.
Il est facile de vérifier que la somme des deux distances
précédentes
est égale à AB et leur proportion  .
Une autre forme de DB (qui nous sera utile) s'obtient en
divisant numérateur et dénominateur par .
Une autre forme de DB (qui nous sera utile) s'obtient en
divisant numérateur et dénominateur par  : :
 (47.384)
(47.384)
Nous savons selon nos calculs précédents que  mais
cela est insuffisant. Nous voulons encore connaître les angles
des sommets A, B, S et
c'est ce à quoi nous allons nous intéresser maintenant. mais
cela est insuffisant. Nous voulons encore connaître les angles
des sommets A, B, S et
c'est ce à quoi nous allons nous intéresser maintenant.
Dans ce cadre, si un satellite en S est en équilibre,
il restera toujours à la même distance de A ou de B.
Le centre de rotation des 3 points est le point D, la masse A elle-même
tourne autour de lui. Si le satellite, en S, reste stabilisé,
les trois corps ont la même période orbitale T. Si S est
immobile dans ce cadre en rotation il ne sera pas soumis à la force
de Coriolis mais uniquement à la force centrifuge, aussi bien de
celle de A que de B.
Notons  la
vitesse de rotation de B et la
vitesse de rotation de B et  la
vitesse de rotation de S. Nous avons alors: la
vitesse de rotation de S. Nous avons alors:
 et et  (47.385)
(47.385)
Nous en tirons que:
 et et  (47.386)
(47.386)
Nous pouvons donc égaler ces deux expressions:
 (47.387)
(47.387)
Cela exprime simplement le fait bien connu que si deux objets
tournent conjointement, le plus éloigné de l'axe est le plus rapide.
Les vitesses sont proportionnelles aux distances de l'axe.
La force centrifuge sur B est en équilibre avec
la force gravitationnelle de A et cela s'exprime par:
 (47.388)
(47.388)
Soit en simplifiant:
 (47.389)
(47.389)
De même, la force centrifuge qui s'applique sur S est:
 (47.390)
(47.390)
Elle est équilibrée par les forces d'attraction  des
corps A et B. Néanmoins, seules les composantes de
ces forces situées sur la ligne R s'opposent efficacement à cette
force centrifuge. D'où: des
corps A et B. Néanmoins, seules les composantes de
ces forces situées sur la ligne R s'opposent efficacement à cette
force centrifuge. D'où:
 (47.391)
(47.391)
et comme:
 et et  (47.392)
(47.392)
Nous avons alors:
 (47.393)
(47.393)
En outre, les forces s'appliquant à S et
perpendiculaires à R doivent
s'annuler. Si non, le corps S suivrait la masse la plus
importante et ne resterait pas en position et ne serait donc plus
en équilibre. Il faut donc que:
 (47.394)
(47.394)
Soit, après substitution et simplification:
 (47.395)
(47.395)
De toutes les équations obtenues jusqu'à maintenant les seules
qui nous dérangent sont celles contenant à la fois
des vitesses et des angles  .
Il faut donc que nous arrivions à éliminer ce qui convient pour
n'avoir que les deux derniers paramètres (soit les angles). .
Il faut donc que nous arrivions à éliminer ce qui convient pour
n'avoir que les deux derniers paramètres (soit les angles).
Pour cela, nous portons au carré:
 (47.396)
(47.396)
Nous multiplions des deux côtés par  et
divisons par et
divisons par  : :
 (47.397)
(47.397)
qui est à rapprocher de:
 (47.398)
(47.398)
Donc en égalant:
 (47.399)
(47.399)
Nous avons donc éliminé la vitesse de B. Maintenant, multiplions
les deux côtés par  et
divisons par et
divisons par  et
multiplions par R: et
multiplions par R:
 (47.400)
(47.400)
à rapprocher de:
 (47.401)
(47.401)
Donc:
 (47.402)
(47.402)
En divisant le tout par  nous
trouvons: nous
trouvons:
 (47.403)
(47.403)
Et comme nous avons démontré au début  que
nous noterons R', nous avons alors: que
nous noterons R', nous avons alors:
 (47.404)
(47.404)
et rappelons que nous avons:
 (47.405)
(47.405)
Soit:
 (47.406)
(47.406)
Ce qui nous permet d'écrire:
 (47.407)
(47.407)
En multipliant par  : :
 (47.408)
(47.408)
Soit:
 (47.409)
(47.409)
Nous pouvons maintenant remarquer une chose (faut le voir...).
Si  (soit
que le triangle ABS est équilatéral) la relation précédente
se simplifie en: (soit
que le triangle ABS est équilatéral) la relation précédente
se simplifie en:
 (47.410)
(47.410)
Or, si le triangle est bien équilatéral, nous avons
alors  .
Dès lors: .
Dès lors:
 (47.411)
(47.411)
Soit ce qui peut s'écrire finalement:
 (47.412)
(47.412)
Ce qui n'est autre que le théorème des sinus
pour le triangle SDB (cf.
chapitre de Trigonométrie) et est donc certain. En
reprenant en arrière, nous pouvons maintenant prouver que
toutes les équations
précédentes
sont satisfaites si et seulement si ABS est équilatéral.
Si nous n'avions pas posé ABS comme équilatéral,
nous aurions obtenu une relation différente du théorème
des sinus, sans vérification
possible, et l'ensemble des équations exigées pour
l'équilibre
au point S n'auraient pu être satisfaites.
Conclusion de la chose... le système donne comme solution:
 (47.413)
(47.413)
ABS (ou ABL peu importe l'écriture), forme alors
un triangle équilatéral. Les deux points d'équilibre sont notés L4
et L5. L4 est situé en avance par rapport à l'astre
de masse la plus petite, et L5 en retard.

Figure: 47.30 - Triangle équilatéral formé par le système
En 2000, 385 astéroïdes en L4 et 188 astéroïdes
en L5
ont été comptabilisés sur l'orbite de Jupiter,
mais situés précisément
selon un triangle équilatéral avec le Soleil et Jupiter
de part et d'autre de Jupiter: ce sont les planètes Troyennes.
Il a également été observé deux
objets au point L5 de Mars découverts en 1990 et
1998.

- Guide de localisation des astres,
C. Gentili, Éditions
EDP Sciences, 1ère édition
ISBN13: 9782759800599 (286 pages) - Imprimé en
2008
- Orbital Mechanics for Engineering Students, Éditions
Elsevier, Howard Curtis
ISBN10: 0750661690 (692 pages) - Imprimé en
2005
 14 14  0 0 |
Commentaires:
Warning: mysql_connect() [function.mysql-connect]: [2002] Connection refused (trying to connect via tcp://crawl801.us.archive.org:3306) in /home/www/f9f6c3f0bb515fb7fa59d2c99a31acd3/web/htmlfr/php/commentaires/config/fonctions.lib.php on line 46
Warning: mysql_connect() [function.mysql-connect]: Connection refused in /home/www/f9f6c3f0bb515fb7fa59d2c99a31acd3/web/htmlfr/php/commentaires/config/fonctions.lib.php on line 46
Warning: mysql_select_db() expects parameter 2 to be resource, boolean given in /home/www/f9f6c3f0bb515fb7fa59d2c99a31acd3/web/htmlfr/php/commentaires/config/fonctions.lib.php on line 47
Warning: mysql_query() expects parameter 2 to be resource, boolean given in /home/www/f9f6c3f0bb515fb7fa59d2c99a31acd3/web/htmlfr/php/commentaires/config/fonctions.lib.php on line 50
Warning: mysql_fetch_array() expects parameter 1 to be resource, null given in /home/www/f9f6c3f0bb515fb7fa59d2c99a31acd3/web/htmlfr/php/commentaires/config/fonctions.lib.php on line 51
[] 
Warning: mysql_close() expects parameter 1 to be resource, boolean given in /home/www/f9f6c3f0bb515fb7fa59d2c99a31acd3/web/htmlfr/php/commentaires/config/fonctions.lib.php on line 58
|
|