|

THÉORIE
DE LA DÉMONSTRATION |
NOMBRES | OPÉRATEURS
ARITHMÉTIQUES
THÉORIE DES NOMBRES
| THÉORIE DES ENSEMBLES |
PROBABILITÉS | STATISTIQUES
Dernière mise à jour de ce chapitre:
2017-12-31 17:55:32 | {oUUID 1.706}
Version: 3.10 Révision 59 | Avancement: ~90%
 vues
depuis le 2012-01-01:
0 vues
depuis le 2012-01-01:
0
 LISTE DES SUJETS TRAITÉS SUR CETTE PAGE
LISTE DES SUJETS TRAITÉS SUR CETTE PAGE
ESTIMATEURS DE VRAISEMBLANCE
Ce qui va suivre est
d'une extrême importance en statistiques et est utilisé énormément
en pratique. Il convient donc d'y accorder une attention toute
particulière! Outre le fait que nous utiliserons cette
technique dans la présent chapitre, nous la retrouverons dans
le chapitre de Méthodes Numériques pour les techniques avancées
de régressions linéaires généralisées ainsi que dans le chapitre
de Génie Industriel dans le cadre de l'estimation des paramètres
de fiabilité.
Nous supposons que nous
disposons d'observations  qui
sont des réalisations de variables aléatoires non biaisées (dans
le sens qu'elles sont choisies aléatoirement parmi un lot) indépendantes qui
sont des réalisations de variables aléatoires non biaisées (dans
le sens qu'elles sont choisies aléatoirement parmi un lot) indépendantes  de
loi de probabilité inconnue mais identique. de
loi de probabilité inconnue mais identique.
Nous allons chercher à estimer
cette loi de probabilité P inconnue à partir des observations  . .
Supposons que nous procédons
par tâtonnements pour estimer la loi de probabilité P inconnue.
Une manière
de procéder est de se demander si les observations  avaient
une probabilité élevée ou non de sortir avec
cette loi de probabilité arbitraire P. avaient
une probabilité élevée ou non de sortir avec
cette loi de probabilité arbitraire P.
Nous devons pour cela calculer
la probabilité conjointe qu'avaient les observations  de
sortir avec les probabilités de
sortir avec les probabilités  .
Cette probabilité conjointe vaut (cf.
chapitre de Probabilités): .
Cette probabilité conjointe vaut (cf.
chapitre de Probabilités):
 (7.1)
(7.1)
en
notant P la loi de probabilité supposée
associée à  .
Il faut avouer qu'il serait alors particulièrement
maladroit, au niveau de la notion intuitive de risque, de
choisir une loi de probabilité (avec
ses paramètres!)
qui minimise cette quantité... .
Il faut avouer qu'il serait alors particulièrement
maladroit, au niveau de la notion intuitive de risque, de
choisir une loi de probabilité (avec
ses paramètres!)
qui minimise cette quantité...
Au contraire, nous allons
chercher les probabilités  (ou
les paramètres de la loi associée) qui
maximisent (ou
les paramètres de la loi associée) qui
maximisent ,
c'est-à-dire qui rende les observations ,
c'est-à-dire qui rende les observations  le
plus vraisemblable possible. le
plus vraisemblable possible.
Nous sommes donc amenés à chercher le (ou les) paramètre(s)
 qui maximise(nt) la quantité:
qui maximise(nt) la quantité:
 (7.2)
(7.2)
et où le paramètre  est
souvent dans les cas scolaires un moment d'ordre un (espérance)
ou d'ordre deux (variance). est
souvent dans les cas scolaires un moment d'ordre un (espérance)
ou d'ordre deux (variance).
Cette quantité L porte le
nom de "vraisemblance".
C'est une fonction du ou des paramètres  et
des observations et
des observations  . .
La ou les valeurs du paramètre  qui
maximisent la vraisemblance qui
maximisent la vraisemblance  sont
appelées "estimateurs
du maximum de vraisemblance" (estimateur MV/EMV). sont
appelées "estimateurs
du maximum de vraisemblance" (estimateur MV/EMV).
Dans le cas très particulier mais formateur de la loi
Normale, un des paramètres  sera
donc la variance (voir un peu plus loin l'exemple concret) et il
peut être considéré comme intuitif au physicien
que pour maximiser la probabilité, l'écart-type doit être
le plus petit possible (pour que le maximum d'évenements
se trouve dans un même intervalle).
Ainsi, lorsque nous calculons un EMV qui est le plus petit parmi
plusieurs possibles, nous parlons alors d'estimateur UMV pour "Uniform
Minimum Variance Unbiased" car leur propre variance
doit
être la plus petite possible. Cela se démontre (mais
c'est peu
élégant) en utilisant la définition de l'Information
de Fisher et du théorème de Fréchet
(ou de Rao-Cramer) qui fait usage de l'inégalité de
Cauchy-Schwartz (cf. chapitre de Calcul Vectoriel)
et de l'analogie entre espérance et produit scalaire...
Cette démonstration
ne sera pas présentée sur ce site Internet. sera
donc la variance (voir un peu plus loin l'exemple concret) et il
peut être considéré comme intuitif au physicien
que pour maximiser la probabilité, l'écart-type doit être
le plus petit possible (pour que le maximum d'évenements
se trouve dans un même intervalle).
Ainsi, lorsque nous calculons un EMV qui est le plus petit parmi
plusieurs possibles, nous parlons alors d'estimateur UMV pour "Uniform
Minimum Variance Unbiased" car leur propre variance
doit
être la plus petite possible. Cela se démontre (mais
c'est peu
élégant) en utilisant la définition de l'Information
de Fisher et du théorème de Fréchet
(ou de Rao-Cramer) qui fait usage de l'inégalité de
Cauchy-Schwartz (cf. chapitre de Calcul Vectoriel)
et de l'analogie entre espérance et produit scalaire...
Cette démonstration
ne sera pas présentée sur ce site Internet.
Faisons quand même cinq
petits exemples (très classiques, utiles et importants
dans l'industrie) avec dans l'ordre d'importance (donc pas forcément
dans l'ordre de facilité...) la fonction de distribution
de Gauss-Laplace (Normale), la fonction de distribution
de Poisson, la distribution Binomiale (et in extenso Géométrique),
la distribution de Weibull et finalement la distribution Gamma.
Remarque: Ces cinq exemples sont importants car utilisés
dans les SPC (maîtrise statistiques de processus) dans différentes
multinationales à travers le monde (cf.
chapitre de Génie Industriel).
ESTIMATEURS DE LA DISTRIBUTION NORMALE
Soit  un
n-échantillon
de variables aléatoires identiquement distribuées supposées
suivre une loi de Gauss-Laplace (loi Normale) de paramètres un
n-échantillon
de variables aléatoires identiquement distribuées supposées
suivre une loi de Gauss-Laplace (loi Normale) de paramètres  et et  . .
Nous recherchons quelles
sont les valeurs des estimateurs du maximum de vraisemblance  qui
maximisent la vraisemblance qui
maximisent la vraisemblance  de
la loi Normale? de
la loi Normale?
Remarque: Il va de soi que les estimateurs du maximum
de vraisemblance
 sont
ici:
 (7.3)
(7.3)
Nous avons démontré plus haut que la densité d'une
variable aléatoire
gaussienne était donnée
par:
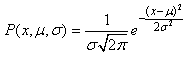 (7.4)
(7.4)
La vraisemblance est alors
donnée
par:
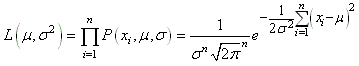 (7.5)
(7.5)
Maximiser une fonction ou
maximiser son logarithme est équivalent donc la "log-vraisemblance"
sera:
 (7.6)
(7.6)
Nous retrouvons par ailleurs souvent dans la littérature la notation:
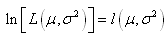 (7.7)
(7.7)
Pour déterminer
les deux estimateurs de la loi Normale, fixons d'abord l'écart-type.
Pour cela, dérivons  par
rapport à par
rapport à  et regardons pour quelle valeur de la moyenne la fonction s'annule.
et regardons pour quelle valeur de la moyenne la fonction s'annule.
Remarque: La dérivéer partielle que nous chercheons à annuler
est souvent appelée la "fonction
score":
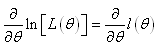 (7.8)
(7.8)
Il nous reste après simplification le terme suivant qui
est égal à zéro:
 (7.9)
(7.9)
Ainsi, l'estimateur du maximum
de vraisemblance de la moyenne (espérance) de la loi Normale
est donc après réarrangement:
 (7.10)
(7.10)
et nous voyons qu'il s'agit simplement de la moyenne arithmétique
(ou appelée aussi "moyenne empirique").
Fixons maintenant la moyenne.
L'annulation de la dérivée de  en
en  conduit à: conduit à:
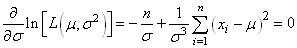 (7.11)
(7.11)
Ce qui nous
permet d'écrire l'estimateur du maximum de vraisemblance
pour l'écart-type
(la variance lorsque la moyenne est connue selon la loi de distribution
supposée elle aussi connue!):
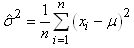 (7.12)
(7.12)
que certains appellent aussi "écart-type
de Pearson"...
Cependant, nous n'avons pas
encore défini ce qu'était un bon estimateur ! Ce que nous entendons
par là:
- Si l'espérance
d'un estimateur est égale à elle-même, nous
disons que cet estimateur est "sans
biais" et c'est bien évidemment ce que nous
cherchons!
- Si l'espérance
d'un estimateur n'est
pas égale à elle-même, nous disons
alors que cet estimateur est "biaisé" et
c'est forcément moins bien...
Dans l'exemple précédent,
la moyenne est donc non biaisée (trivial car la moyenne
de la moyenne arithmétique est égale à elle-même).
Mais qu'en est-il de la variance (in extenso de l'écart-type)
?
Un petit calcul simple par linéarité de l'espérance
(puisque les variables aléatoires sont identiquement distribuées)
va nous donner la réponse
dans le cas où la
moyenne théorique est approchée
comme dans la pratique (industrie) par l'estimateur de la moyenne
(cas le plus fréquent).
Nous avons donc le calcul de l'espérance
de la "variance empirique":
 (7.13)
(7.13)
Or, comme les variables sont équidistribuées:
 (7.14)
(7.14)
Et nous avons (relation de Huyghens):
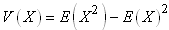 (7.15)
(7.15)
ainsi que:
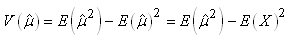 (7.16)
(7.16)
où la deuxième relation ne peut s'écrire que parce
que nous utilisons l'estimateur du maximum de vraisemblance de
la moyenne (moyenne
empirique). D'où:
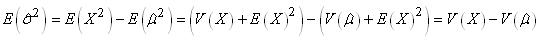 (7.17)
(7.17)
et comme:
 et et  (7.18)
(7.18)
Nous avons finalement:
 (7.19)
(7.19)
nous avons donc un biais de moins une fois l'erreur-standard:
 (7.20)
(7.20)
nous disons alors que cet estimateur à un biais négatif (il sous-estime
la vraie valeur!).
Nous noterons également
que l'estimateur tend vers un estimateur sans
biais (E.S.B.) lorsque le nombre d'individus tend
vers l'infini  .
Nous disons alors que nous avons un "estimateur
asymptotiquement non biaisé" ou "estimateur
asymptotiquement débiaisé". .
Nous disons alors que nous avons un "estimateur
asymptotiquement non biaisé" ou "estimateur
asymptotiquement débiaisé".
Il est important
de prendre note que nous avons démontré que
la variance empirique tend vers la variance théorique
quand n tend
vers l'infini et ce... que les données suivent une loi Normale
ou non!
Remarque: Un estimateur est aussi dit " estimateur
consistant" s'il converge en probabilité, lorsque  ,
vers la vraie valeur du paramètre.
De par les propriétés de
l'espérance, nous avons alors:
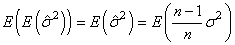 (7.21)
(7.21)
Il vient alors:
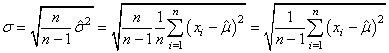 (7.22)
(7.22)
que certains appellent
aussi "écart-type standard"...
(à ne pas confondre avec "l'erreur-standard" que nous verrons plus
loin).
Nous avons donc finalement pour résumer
les deux résultats importants suivants:
1. "L'estimateur du maximum de vraisemblance
biaisé"
ou appelé également "écart-type
empirique" ou encore "écart-type échantillonnal" ou
encore "écart-type de Pearson"
... et donc donné par:
 (7.23) (7.23)
lorsque  .
Nous retrouvons cet écart-type suivant les contextes (par
tradition) noté de cinq autres différentes façons
qui sont: .
Nous retrouvons cet écart-type suivant les contextes (par
tradition) noté de cinq autres différentes façons
qui sont:
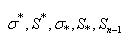 (7.24)
(7.24)
et même parfois (mais c'est très malheureux
car cela génère alors souvent de la confusion avec
l'estimateur non biaisé)  ou S. ou S.
2. "L'estimateur
du maximum de vraisemblance non biaisé" ou
appelé
également "écart-type
standard" avec la "correction
de Bessel" (le -1 au dénominateur est la correction en
question...):
 (7.25)
(7.25)
qui comme nous le voyons est un estimateur convergent (quand n tend
vers l'infini celui-ci tend vers l'estimateur
du maximum de vraisemblance biaisé).
Nous retrouvons cet écart-type suivant les contextes (par
tradition) noté de trois autres différentes façons
qui sont:
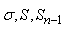 (7.26)
(7.26)
Nous retrouverons ces deux dernières notations souvent
dans les tables et dans de nombreux logiciels et que nous utiliserons
plus bas
dans les développements des intervalles de confiance et
des tests d'hypothèses!
Par
exemple, dans la version française de de Microsoft Excel 11.8346
l'estimateur biaisé est
donné par
la fonction ECARTYPEP( ) et le non biaisé par ECARTTYPE(
).
Au total, cela nous fait donc trois estimateurs pour la même
quantité!! Comme dans l'écrasante majorité des
cas de l'industrie la moyenne théorique n'est pas connue,
nous utilisons le plus souvent les deux dernières relations
encadrées
ci-dessus. Maintenant, c'est là que c'est le plus vicieux:
lorsque nous calculons le biais des
deux estimateurs, le premier est biaisé, le second ne
l'est pas. Donc nous aurions tendance à n'utiliser que le
second. Que nenni! Car nous pourrions aussi parler de la variance
et de
la précision d'un estimateur, qui sont aussi des critères
importants pour juger
de la qualité d'un estimateur par rapport à un autre.
Si nous faisions le calcul de la variance des deux estimateurs,
alors
le premier,
qui est
biaisé, a une variance plus petite que le second qui est
sans biais! Tout ça pour dire que
le critère du biais n'est pas (et de loin) le seul à étudier
pour juger de la qualité d'un estimateur.
Enfin, il est important de se rappeler que le facteur -1 du dénominateur
de l'estimateur du maximum de vraisemblance non biaisé provient
du fait qu'il fallait corriger l'espérance de l'estimateur
biaisé
à la base minoré de une fois l'erreur-standard!
ESTIMATEURS DE LA DISTRIBUTION DE POISSON
En utilisant la même méthode que pour la loi Normale (Gauss-Laplace),
nous allons donc rechercher les estimateurs du maximum de vraisemblance
de la loi de Poisson qui rappelons-le, est donnée par:
 (7.27)
(7.27)
Dès lors, la vraisemblance est donnée par:
 (7.28)
(7.28)
Maximiser une fonction ou maximiser son logarithme est équivalent
donc:
 (7.29)
(7.29)
Nous cherchons maintenant à la maximiser:
 (7.30)
(7.30)
et obtenons donc son unique estimateur du maximum de vraisemblance
qui sera:
 (7.31)
(7.31)
Il est tout à fait normal de retrouver dans cet exemple
didactique la moyenne empirique, car c'est le meilleur estimateur
possible pour le paramètre de la loi de Poisson (qui représente
aussi l'espérance d'une loi de Poisson).
Sachant que l'écart-type de cette distribution particulière
(voir plus haut lors de notre développement de la loi
de Poisson) n'est que la racine carrée
de la moyenne, nous avons alors pour l'écart-type du maximum
de vraisemblance:
 (7.32)
(7.32)
Remarque:
Nous montrons de la même manière des résultats
identiques pour la loi exponentielle très utilisée
en maintenance préventive et
fiabilité!
ESTIMATEUR DE LA DISTRIBUTION BINOMIALE (ET GÉOMÉTRIQUE)
En utilisant la même méthode que pour la loi Normale (Gauss-Laplace)
et la loi de Poisson, nous allons donc rechercher l'estimateur
du maximum de vraisemblance de la loi Binomiale qui rappelons-le,
est donnée par:
 (7.33)
(7.33)
Dès lors, la vraisemblance est donnée par:
 (7.34)
(7.34)
Il convient de se rappeler que le facteur qui suit
le terme combinatoire exprime déjà les variables
successives selon ce que nous avons vu lors de notre étude
de la fonction de distribution de Bernoulli et de la fonction binomiale.
D'où la disparition du produit dans la dernière égalité précédente.
Maximiser une fonction ou maximiser son logarithme est équivalent
donc:
 (7.35)
(7.35)
Nous cherchons maintenant à la maximiser:
 (7.36)
(7.36)
Le lecteur aura peut-être remarqué que le coefficient binomial
a disparu. Dès lors, nous en déduisons immédiatement
que l'estimateur de la loi binomiale sera le même que celui
de la loi géométrique.
Ce qui donne:
 (7.37)
(7.37)
d'où nous tirons l'estimateur du maximum de vraisemblance
qui sera donc la simple moyenne empirique:
 (7.38)
(7.38)
Ce résultat est assez intuitif si l'on considère
l'exemple classique d'une pièce de monnaie qui a une chance
sur deux de tomber sur une de ces faces. La probabilité p étant
le nombre de fois k où une face donnée a été observée
sur le nombre d'essais total (toutes faces confondues).
Remarque: Dans la pratique, il n'est pas aussi simple
d'appliquer ces estimateurs! Il faut bien réfléchir
lesquels sont les plus adaptés à une expérience
donnée
et idéalement calculer également l'erreur quadratique
moyenne (erreur-standard) de chacun des estimateurs de la moyenne
(comme nous l'avons déjà fait pour la moyenne empirique
plus tôt). Bref c'est un long travail de réflexion.
ESTIMATEURS DE LA DISTRIBUTION DE WEIBULL
Nous avons vu dans le chapitre de Génie Industriel une étude
très détaillée de la loi de Weibull à trois
paramètres avec son écart-type
et son espérance car nous avions précisé qu'elle était
assez utilisée
dans le domaine de l'ingénierie de la fiabilité.
Malheureusement les trois paramètres de cette loi nous
sont en pratique inconnus. A l'aide des estimateurs nous pouvons
cependant déterminer l'expression de deux des trois en supposant 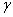 comme étant
nul. Cela nous donne donc la loi de Weibull dite "loi de Weibull à deux
paramètres" suivante: comme étant
nul. Cela nous donne donc la loi de Weibull dite "loi de Weibull à deux
paramètres" suivante:
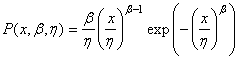 (7.39)
(7.39)
avec pour rappel 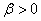 et et 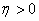 . .
Dès lors la vraisemblance est donnée par:
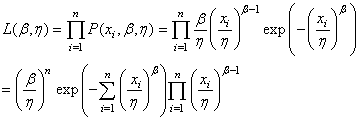 (7.40)
(7.40)
Maximiser une fonction ou maximiser son logarithme est équivalent
donc:
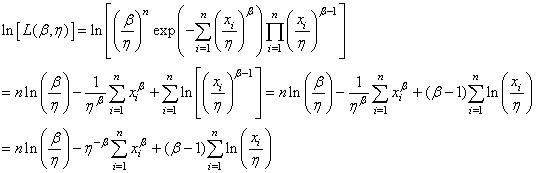 (7.41)
(7.41)
Cherchons maintenant à maximiser cela en se rappelant que (cf.
chapitre de Calcul Différentiel et Intégral):
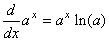 et et 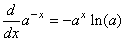 (7.42)
(7.42)
d'où:
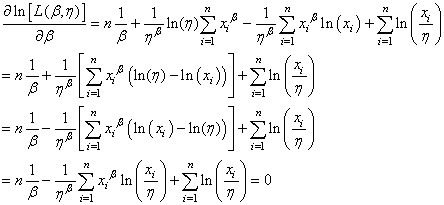 (7.43)
(7.43)
Et nous avons pour le deuxième paramètre:
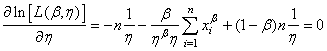 (7.44)
(7.44)
d'où:
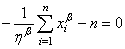 (7.45)
(7.45)
Finalement avec les écritures correctes (et dans l'ordre de résolution
dans la pratique):
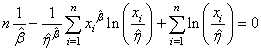 et et 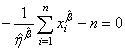 (7.46)
(7.46)
La résolution de ces équations implique de lourds
calculs et nous ne pouvons a priori rien en tirer dans des tableurs
classiques comme Microsoft Excel ou Calc de Open Office sans
faire de la programmation.
On prend alors une approche différente en écrivant notre loi
de Weibull à deux paramètres ainsi:
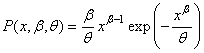 (7.47)
(7.47)
avec pour rappel 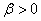 et et 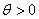 . .
Dès lors la vraisemblance est donnée par:
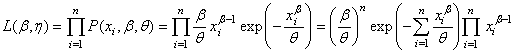 (7.48)
(7.48)
Maximiser une fonction ou maximiser son logarithme est équivalent
donc:
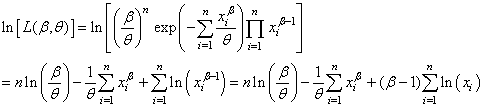 (7.49)
(7.49)
Cherchons maintenant à maximiser cela en se rappelant que (cf.
chapitre de Calcul Différentiel et Intégral):
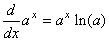 et et 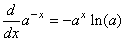 (7.50)
(7.50)
d'où:
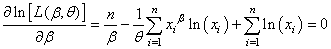 (7.51)
(7.51)
Et nous avons pour le deuxième paramètre:
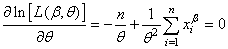 (7.52)
(7.52)
Il est alors immédiat que:
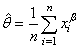 (7.53)
(7.53)
injecté dans la relation:
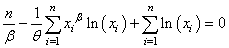 (7.54)
(7.54)
Il vient:
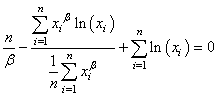 (7.55)
(7.55)
en simplifiant:
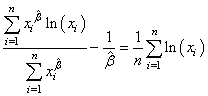 (7.56)
(7.56)
La résolution des deux équations (dans l'ordre de haut en bas):
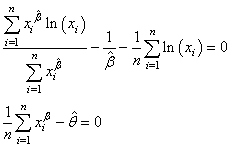 (7.57)
(7.57)
peut très facilement être calculée avec l'outil
Valeur Cible de Microsoft Excel ou Calc de Open Office.
ESTIMATEURS DE LA DISTRIBUTION GAMMA
Nous allons utiliser ici une technique appelée "méthode
des moments" pour déterminer les estimateurs des
paramètres de la loi Gamma.
Supposons que X1, ..., Xn sont
des variables aléatoires indépendantes et identiquement distribuées
selon la loi Gamma avec pour densité:
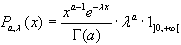 (7.58)
(7.58)
Nous cherchons à estimer 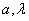 .
Pour cela, nous déterminons d'abord quelques moments théoriques. .
Pour cela, nous déterminons d'abord quelques moments théoriques.
Le premier moment est l'espérance qui comme nous l'avons démontré vaut:
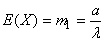 (7.59)
(7.59)
et le second moment, l'espérance du carré de la variable aléatoire,
est comme nous l'avons démontré implicitement lors de la démonstration
de la variance de la loi Gamma:
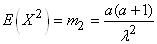 (7.60)
(7.60)
Nous exprimons ensuite la relation entre les paramètres et les
moments théoriques:
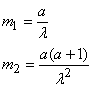 (7.61)
(7.61)
La résolution donne:
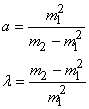 (7.62)
(7.62)
Une fois ce système établi, la méthode des moments consiste à utiliser
les moments empiriques, en l'occurrence pour notre exemple les
deux premiers, 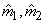 : :
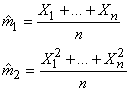 (7.63)
(7.63)
que nous posons égaux aux moments théoriques vrais... Dès lors,
il vient:
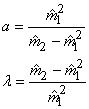 (7.64)
(7.64)
FACTEUR DE CORRECTION SUR POPULATION FINIE
Maintenant démontrons un autre résultat qui nous
sera indispensables dans certains tests statistiques que nous verrons
plus loin.
Supposons que nous avons une population de N individus
que nous représentons par l'ensemble 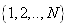 et
une variable aléatoire X qui est donc une application de et
une variable aléatoire X qui est donc une application de 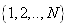 dans dans 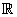 .
Nous posons .
Nous posons 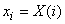 .
La moyenne de X est alors donnée par: .
La moyenne de X est alors donnée par:
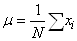 (7.65)
(7.65)
La variance de X est par définition:
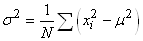 (7.66)
(7.66)
Considérons à présent l'ensemble E des échantillons 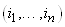 de
taille n pris dans de
taille n pris dans 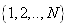 avec avec 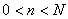 .
Chaque individu a une probabilité d'être tiré égale à: .
Chaque individu a une probabilité d'être tiré égale à:
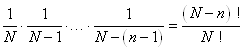 (7.67)
(7.67)
Nous nous intéressons à la variable aléatoire 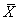 définie
sur E et étant égale à la moyenne de l'échantillon. Plus
précisément: définie
sur E et étant égale à la moyenne de l'échantillon. Plus
précisément:
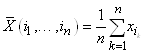 (7.68)
(7.68)
Afin de calculer la variance 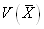 ,
nous allons
exprimer ,
nous allons
exprimer 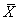 comme
somme de variables aléatoires. En effet si nous définissons les variables comme
somme de variables aléatoires. En effet si nous définissons les variables 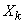 avec avec 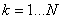 par: par:
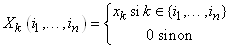 (7.69)
(7.69)
Nous avons naturellement (donc de la par la définition précédente):
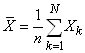 (7.70)
(7.70)
et donc il vient:
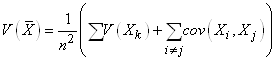 (7.71)
(7.71)
Les variables aléatoires 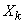 ne
sont pas indépendantes deux à deux, en effet comme nous allons
le voir, leurs covariances ne sont pas nulles si N est
fini. Dans le cas contraire (covariance nulle), nous retrouvons
un résultat déjà démontré plus haut: ne
sont pas indépendantes deux à deux, en effet comme nous allons
le voir, leurs covariances ne sont pas nulles si N est
fini. Dans le cas contraire (covariance nulle), nous retrouvons
un résultat déjà démontré plus haut:
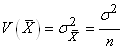 (7.72)
(7.72)
Il nous faut donc calculer les variances 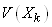 et
les covariances et
les covariances 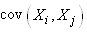 . .
Pour ce faire nous allons utiliser la relation de Huyghens et
nous allons commencer par calculer l'espérance 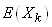 : :
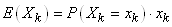 (7.73)
(7.73)
Or 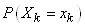 est
la probabilité qu'un échantillon contienne k. Cette probabilité vaut
bien évidemment est
la probabilité qu'un échantillon contienne k. Cette probabilité vaut
bien évidemment 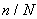 et
par suite: et
par suite:
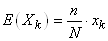 (7.74)
(7.74)
De la même façon nous obtenons:
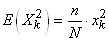 (7.75)
(7.75)
Nous pouvons donc calculer la variance 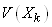 : :
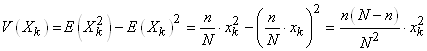 (7.76)
(7.76)
Pour calculer les covariances avons à présent besoin de calculer
les espérances 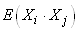 : :
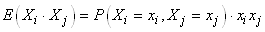 (7.77)
(7.77)
Or 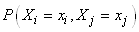 est
la probabilité qu'un échantillon contienne i et j.
Cette probabilité vaut bien évidemment: est
la probabilité qu'un échantillon contienne i et j.
Cette probabilité vaut bien évidemment:
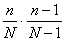 (7.78)
(7.78)
et par suite:
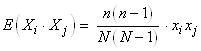 (7.79)
(7.79)
Nous pouvons à présent calculer les covariances:
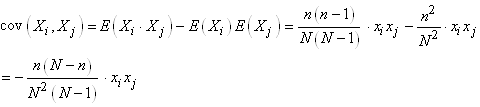 (7.80)
(7.80)
Nous sommes maintenant en mesure de calculer 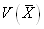 : :
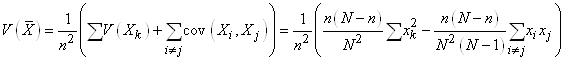 (7.81)
(7.81)
En utilisant le résultat démontré juste plus
haut:
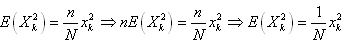 (7.82)
(7.82)
et en l'injectant dans la relation de Huyghens:
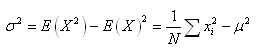 (7.83)
(7.83)
nous pouvons alors écrire:
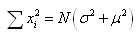 (7.84)
(7.84)
Pour la double somme 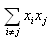 , nous avons: , nous avons:
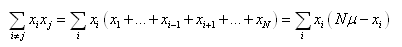 (7.85)
(7.85)
Dès lors:
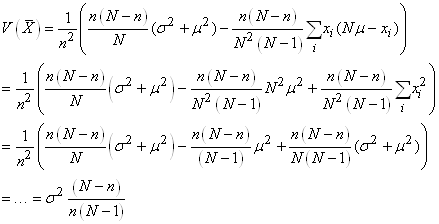 (7.86)
(7.86)
Et donc:
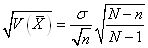 (7.87)
(7.87)
Le terme:
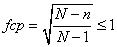 (7.88)
(7.88)
que nous avons déjà rencontré lors de notre étude la loi hypergéométrique
est appelé "facteur de correction sur
population finie" et il a pour effet de réduire l'erreur-standard
d'autant plus que n est grand.
INTERVALLES DE CONFIANCE
Jusqu'à maintenant nous avons toujours déterminé les différents
estimateurs de vraisemblance ou estimateurs simples (variance, écart-type) à partir
de lois (fonctions) statistiques théoriques ou mesurées sur toute
une population de données.
Définition: Un "intervalle
de confiance"
est un couple de nombres qui définit (a posteriori) une
plage de valeurs possibles avec une certaine probabilité cumulée
pour un estimateur (ponctuel) d'un indicateur statistique donné par
un échantillon
d'une expérience (plage
calculée le plus souvent à l'aide
de paramètres vrais mesurés). Il s'agit du cas le
plus fréquent
en statistiques.
Nous allons maintenant aborder qui consiste à se demander assez
naturellement quelles doivent être les tailles des échantillons
de nos données mesureés pour avoir une certaine validité (intervalle
de confiance I.C.) de nos estimateurs ou encore quel écart-type
ou fractile dans une loi Normale centrée réduite
(grand nombre d'individus), du Khi-deux, de Student ou de Fisher
correspond un certain intervalle de confiance (nous verrons ces
deux derniers cas de faibles échantillons dans la partie
traitant de l'analyse de la variance ou ANOVA) lorsque la variance
ou la moyenne est connue ou respectivement inconnue sur l'ensemble
ou une partie de la population donnée.
Indiquons que ces intervalles de confiance utilisent souvent le
théorème central limite démontré plus
loin (afin d'éviter toute frustration) et que les développements
que nous allons faire maintenant nous seront également utiles
dans le domaine des Tests d'Hypothèses qui ont une place
majeure en statistique!
Enfin, indiquons que de très nombreuses organisations (privées
ou étatiques) font des statistiques fausses car les hypothèses
et conditions d'utilisation de ces intervalles de confiance (et
in extenso les tests d'hypothèses qui en découlent) ne sont pas
rigoureusement vérifiées
ou simplement omises ou pire encore, toute la base (les mesures)
n'est pas collectée dans les règles de l'art (fiabilisation
de la collecte de données par des protocoles scientifiques
reproductibles et validés par les pairs).
Enfin, indiquons que de très nombreuses organisations
(privées
ou étatiques) font des statistiques fausses car les hypothèses
et conditions d'utilisation ne sont pas rigoureusement vérifiées
ou simplement omises ou pire encore, toute la base (les mesures)
ne sont pas collectées dans les règles de l'art (fiabilisation
de la collecte de données).
Remarque: Le praticien doit être
très prudent
quant à au
calcul des intervalles de confiance et à l'utilisation des
tests d'hypothèses
dans la pratique. Raison pour laquelle, afin d'éviter toute
erreur triviale d'utilisation ou d'interprétation, il est
important de se référer aux normes suivantes par
exemple: ISO 2602:1980 (Interprétation
statistique de résultats d'essais - Estimation de la moyenne
- Intervalle de confiance), ISO 2854:1976 (Interprétation
statistique des données - Techniques d'estimation et tests
portant sur des moyennes et des variances), ISO 3301:1975 (Interprétation
statistique des données - Comparaison de deux moyennes dans
le cas d'observations appariées), ISO 3494:1976 (Interprétation
statistique des données -- Efficacité des tests portant
sur des moyennes et des variances), ISO 5479:1997 (Interprétation
statistique des données - Tests pour les écarts à la
distribution normale), ISO 10725:2000 + ISO 11648-1:2003 + ISO 11648-2:2001
(Plans et procédures
d'échantillonnage pour acceptation pour le contrôle
de matériaux en vrac), ISO 11453:1996 (Interprétation
statistique des données - Tests et intervalles de confiance
portant sur les proportions), ISO 16269-4:2010 (Interprétation
statistique des données - Détection et traitement
des valeurs aberrantes), ISO 16269-6:2005 (Interprétation
statistique des données - Détermination
des intervalles statistiques de tolérance), ISO 16269-8:2004
(Interprétation statistique des données - Détermination
des intervalles de prédiction), ISO/TR 18532:2009 (Lignes
directrices pour l'application des méthodes statistiques à la
qualité et à la normalisation industrielle).
I.C. SUR LA MOYENNE AVEC VARIANCE THÉORIQUE CONNUE
Commençons par le cas le plus simple et le plus courant
qui est la détermination du nombre d'individus pour avoir
une certaine confiance dans la moyenne des mesures effectuées
d'une variable aléatoire supposée suivre une loi
Normale.
D'abord rappelons que nous avons démontré au début
de ce chapitre que l'erreur-type (écart-type à la
moyenne) était sous l'hypothèses de variables indépendantes
et identiquement distribuées (i.i.d.):
 (7.89)
(7.89)
Maintenant, avant d'aller plus loin, considérons X comme
une variable aléatoire suivant une loi Normale de moyenne  et
d'écart-type et
d'écart-type  .
Nous souhaiterions que la variable aléatoire ait par exemple 95%
de probabilité cumulée de se trouver dans un intervalle symétrique
borné donné. Ce qui s'exprime donc sous la forme suivante: .
Nous souhaiterions que la variable aléatoire ait par exemple 95%
de probabilité cumulée de se trouver dans un intervalle symétrique
borné donné. Ce qui s'exprime donc sous la forme suivante:
 (7.90)
(7.90)
Remarque: Donc
avec un intervalle de confiance de 95% vous aurez raison 19 fois
sur 20, ou n'importe quel autre niveau de confiance
ou niveau de risque  (1-niveau
de confiance, soit 5%) que vous vous serez fixé à l'avance.
En moyenne, vos conclusions seront donc bonnes, mais nous ne pourrons
jamais savoir si une décision particulière est bonne!
Si le niveau de risque est très faible mais que l'événement
a quand même lieu, les spécialistes parlent alors de " grande
déviation" ou de " black
swan" (cygne noir). La gestion des valeurs aberrantes
est traitée dans la norme ISO 16269-4:2010 Détection
et traitement des valeurs aberrantes que tout ingénieur
faisant des statistiques en entreprise se doit de respecter.
En centrant et réduisant la variable aléatoire:
 (7.91)
(7.91)
Notons maintenant Y la variable centrée réduite:
 (7.92)
(7.92)
Puisque la loi Normale centrée réduite est symétrique:
 (7.93)
(7.93)
D'où:
 (7.94)
(7.94)
A partir de là en lisant dans les tables numériques
de la loi Normale centrée réduite (ou en utilisant
un simple tableur), nous avons pour satisfaire cette égalité que:
 (7.95)
(7.95)
Ce qui s'obtient facilement avec la version anglaise de Microsoft
Excel 11.8346 en utilisant la fonction: -NORMSINV((1-0.95)/2).
Donc:
 (7.96)
(7.96)
Ce qui est noté de façon traditionnelle dans le
cas général autre
que 95% par (Z étant la variable aléatoire
correspondant donc
à la moitié du quantile du seuil fixé de la loi Normale centrée
réduite):
 (7.97)
(7.97)
Or, considérons que la variable X sur laquelle
nous souhaitons faire de l'inférence statistique est justement
la moyenne (et nous démontrerons plus loin que celle-ci
suit une loi Normale centrée
réduite). Dès
lors:
 (7.98)
(7.98)
Nous en tirons la taille de l'échantillon:
 (7.99)
(7.99)
dont nous prenons évidemment (normalement...) la valeur
entière
supérieure…
Cette dernière notation est plus souvent
écrite sous la forme suivante mettant mieux en évidence
la largeur de l'intervalle de confiance à un niveau  sous-jacent: sous-jacent:
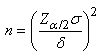 (7.100)
(7.100)
Relation appelée "effectif de
l'échantillon pour estimation par loi Normale".
Ainsi, nous pouvons maintenant savoir le nombre d'individus à avoir
pour s'assurer un intervalle de précision  (marge
d'erreur) autour de la moyenne et pour qu'un pourcentage donné des
mesures se trouvent dans cet intervalle et en supposant l'écart-type
théorique (marge
d'erreur) autour de la moyenne et pour qu'un pourcentage donné des
mesures se trouvent dans cet intervalle et en supposant l'écart-type
théorique  connu
(ou imposé) d'avance (typiquement utilisé dans l'ingénierie
de la qualité ou les instituts de sondages/enquêtes). connu
(ou imposé) d'avance (typiquement utilisé dans l'ingénierie
de la qualité ou les instituts de sondages/enquêtes).
Dans le cas des sondages/enequêtes où la population n'est pass
assez grande pour considéréer que nous avons un échantillonnage
avec remise, nous parlons devons alors introduire la facteur fpc que
nous avons démontré plus haut (nous parlons alors dans PSSR pour
"plan de sondage sans remise"). Il vient alors:
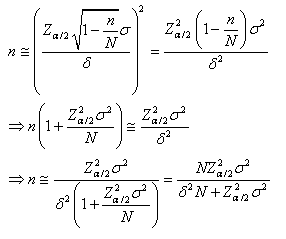 (7.101)
(7.101)
Autrement dit, nous pouvons calculer le nombre n d'individus à mesurer
pour s'assurer un intervalle de confiance donné
(associé à Z) de la moyenne mesurée
en supposant l'écart-type théorique connu (ou
imposé) et en souhaitant un
précision de  en
valeur absolue sur la moyenne. en
valeur absolue sur la moyenne.
Cependant... en réalité, la variable Z provient du théorème
central limite (voir plus bas) qui donne pour un échantillon de
grande taille (approximativement):
 (7.102)
(7.102)
En réarrangeant nous obtenons:
 (7.103)
(7.103)
et comme Z peut être négatif ou positif alors il est plus
censé d'écrire cela sous la forme:
 (7.104)
(7.104)
Soit:
 (7.105)
(7.105)
que les ingénieurs notent parfois:
 (7.106)
(7.106)
avec LCL étant la lower confidence limit et UCL la upper confidence
limit. C'est de la terminologie Six Sigma (cf.
chapitre de Génie Industriel).
Et nous venons de voir plus avant que pour avoir un intervalle
de confiance à 95% nous devrions avoir Z=1.96.
Et puisque la loi Normale est symétrique:
 (7.107)
(7.107)
Cela se note finalement:
 (7.108)
(7.108)
Comme nous l'avons déjà mentionné, et nous
le démontrerons un
peu plus loin, la moyenne arithmétique centrée réduite
d'une séries de variables aléatoires indépendantes
et identiquement distribuées
de variance
fini suit asymptotiquement une loi Normale centrée réduite,
alors l'intervalle de confiance ci-dessus a une portée très
générale!
Raison pour laquelle nous parlons parfois de "d'intervalle
de confiance asymptotique de la moyenne".
Ces intervalles ont évidemment
pour origine que nous travaillons très souvent en statistiques
sur des échantillons et non sur toute la population disponible.
L'échantillonage choisi influe donc sur l'estimateur ponctuel.
Nous parlons alors de "fluctuation d'échantillonage".
Dans le cas particulier d'un I.C. (intervalle
de confiance) à 95%, la dernière relation s'écrit:
 (7.109)
(7.109)
Parfois nous retrouvons l'inégalité antéprécédente sous la forme équivalente
suivante:
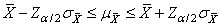 (7.110)
(7.110)
ou encore plus rarement sous la forme générale
suivante (que l'on retrouve pour toutes les intervalles):
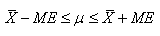 (7.111)
(7.111)
où ME signifie "marge
d'erreur".
Nous sommes ainsi capables maintenant d'estimer
des tailles de population nécessaires à obtenir un
certain niveau de confiance  dans
un résultat, soit d'estimer
dans quel intervalle de confiance se trouve la moyenne théorique
en connaissant la moyenne
expérimentale (empirique) et l'estimateur du maximum de
vraisemblance de l'écart-type. Nous pouvons bien évidemment
dès lors aussi déterminer la probabilité avec
laquelle la moyenne est en dehors d'un certain intervalle... (l'un
comme l'autre étant
beaucoup utilisés dans l'industrie). dans
un résultat, soit d'estimer
dans quel intervalle de confiance se trouve la moyenne théorique
en connaissant la moyenne
expérimentale (empirique) et l'estimateur du maximum de
vraisemblance de l'écart-type. Nous pouvons bien évidemment
dès lors aussi déterminer la probabilité avec
laquelle la moyenne est en dehors d'un certain intervalle... (l'un
comme l'autre étant
beaucoup utilisés dans l'industrie).
Enfin, signalons que du résultat précédent,
nous déduisons immédiatement
par la propriété de
stabilité de la loi Normale (démontrée plus
haut) le test suivant que nous retrouvons dans de très nombreux
logiciels de statistiques:
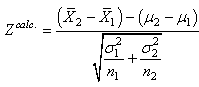 (7.112)
(7.112)
appelé "test
Z bilatéral sur
la différence de deux moyennes" avec l'intervalle de
confiance correspondant:
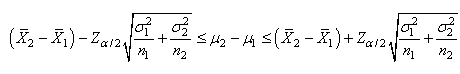 (7.113)
(7.113)
Et ce n'est pas parce que deux moyennes sont significativement
différentes que leurs intervalles de tolérance ne
se superposent pas! Comme le montre le graphique ci-dessous obtenu
avec le logiciel
Minitab 16 où le test-Z de la différence est
significative à 95%:
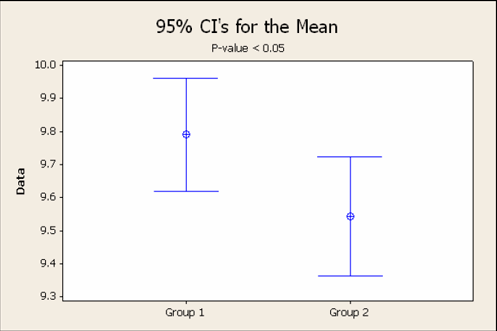
Figure: 7.1 - Illustration de la superposition d'intervalle de tolérance à 95%
alors que leur moyenne est significativement différente
à un seuil de confiance de 95%.
Remarque: La taille de la population
mère
pour les relations développées plus haut n'entre
pas en ligne de compte dans le calcul des intervalles de confiance
ni dans celui de la taille de l'échantillon, et pour cause,
elle est considérée infinie. Il faut donc faire attention à ne
pas avoir parfois des tailles d'échantillons qui sont plus
grandes que la population mère réelle possible...
I.C. SUR LA VARIANCE AVEC MOYENNE THÉORIQUE
CONNUE
Commençons par démontrer une propriété fondamentale
de la loi du Khi-deux:
Si une variable aléatoire X suit une loi Normale centrée
réduite  alors
son carré suit une loi du Khi-deux de degré de liberté 1: alors
son carré suit une loi du Khi-deux de degré de liberté 1:
 (7.114)
(7.114)
Ce résultat est parfois appelé "statistique
de Wald" et tout test statistique l'utilisant directement
(on devrait plutôt parler de "famille de tests")
peut être rangé
sous
la dénomination
de "test de Wald" (pour un
exemple concret voir le test de Cochran-Mantel-Haenszel
dans le chapitre de Méthodes Numériques).
Démonstration:
Pour démontrer cette propriété, il suffit de calculer la densité de
la variable aléatoire  avec avec  .
Or, si .
Or, si  et
si nous posons et
si nous posons  ,
alors pour tout ,
alors pour tout  nous
obtenons: nous
obtenons:
 (7.115)
(7.115)
Puisque la loi Normale centrée réduite est symétrique
par rapport à 0
pour la variable aléatoire X, nous pouvons écrire:
 (7.116)
(7.116)
En notant  la
fonction de répartition de la loi Normale centrée réduite (sa probabilité cumulée
en d'autres termes pour rappel...), nous avons: la
fonction de répartition de la loi Normale centrée réduite (sa probabilité cumulée
en d'autres termes pour rappel...), nous avons:
 (7.117)
(7.117)
et comme:
 (7.118)
(7.118)
alors:
 (7.119)
(7.119)
La fonction de répartition de la variable aléatoire
(probabilité cumulée)  est
donc donnée par: est
donc donnée par:
 (7.120)
(7.120)
si y est supérieur ou égal à zéro,
nulle si y inférieur à zéro.
Nous noterons cette répartition  pour
la suite des calculs. pour
la suite des calculs.
Puisque la fonction de distribution est la dérivée de la fonction
de répartition et que X suit une loi Normale centrée réduite
alors nous avons pour la variable aléatoire X:
 (7.121)
(7.121)
et il s'ensuit pour la loi de distribution de Y (qui
est donc le carré de X pour rappel!):
 (7.122)
(7.122)
cette dernière expression correspond exactement à la
relation que nous avions obtenue lors de notre étude de
la loi du Khi-deux en imposant un degré de liberté unité.
Le théorème est donc bien démontré,
à savoir
que si X suit une
loi Normale centrée réduite alors son carré suit
une loi du Khi-deux à 1
degré de liberté tel que:
 (7.123)
(7.123)
 C.Q.F.D. C.Q.F.D.
Ce type de relation est utilisé dans les processus industriels
et leur contrôle (cf. chapitre de Génie
Industriel).
Nous allons maintenant utiliser un résultat démontré lors
de notre étude de la loi Gamma. Nous avons effectivement
vu plus haut que la somme de deux variables aléatoires suivant
une loi Gamma suit aussi une loi Gamma dont les paramètres
s'additionnent:
 (7.124)
(7.124)
Comme la loi du Khi-deux n'est qu'un cas particulier de la loi
Gamma, le même résultat s'applique.
Pour être plus précis, cela revient à dire:
Si  sont
des variables aléatoires indépendantes (!) et identiquement distribuées
N(0,1) alors
par extension de la démonstration précédente
où nous avons montré que: sont
des variables aléatoires indépendantes (!) et identiquement distribuées
N(0,1) alors
par extension de la démonstration précédente
où nous avons montré que:
 (7.125)
(7.125)
et de la propriété d'addition de la loi Gamma,
la somme de leurs carrés suit alors une loi du Khi-deux
de degrés de liberté k telle
que:
 (7.126)
(7.126)
Ainsi, la loi du  à k degrés
de liberté est la loi de probabilité de la somme
des carrés de k variables
normales centrées réduites linéairement indépendantes
entre elles. Il s'agit de la propriété de linéarité de
la loi du Khi-deux (implicitement de la linéarité de
la loi Gamma)! à k degrés
de liberté est la loi de probabilité de la somme
des carrés de k variables
normales centrées réduites linéairement indépendantes
entre elles. Il s'agit de la propriété de linéarité de
la loi du Khi-deux (implicitement de la linéarité de
la loi Gamma)!
Maintenant voyons une autre propriété importante
de la loi du Khi-deux: Si  sont
des variables aléatoires indépendantes et identiquement
distribuées sont
des variables aléatoires indépendantes et identiquement
distribuées  (donc
de même moyenne et même écart-type et suivant une loi Normale)
et si nous notons l'estimateur du maximum de vraisemblance de la
variance: (donc
de même moyenne et même écart-type et suivant une loi Normale)
et si nous notons l'estimateur du maximum de vraisemblance de la
variance:
 (7.127)
(7.127)
alors, le rapport de la variable aléatoire  sur
l'écart-type supposé connu de l'ensemble de la population
(dit "écart-type vrai" ou "écart-type
théorique" pour bien différencier!)
multiplié par
le nombre d'individus n de
la population suit une loi du Khi-deux de degré n telle
que: sur
l'écart-type supposé connu de l'ensemble de la population
(dit "écart-type vrai" ou "écart-type
théorique" pour bien différencier!)
multiplié par
le nombre d'individus n de
la population suit une loi du Khi-deux de degré n telle
que:
 (7.128)
(7.128)
Ce résultat est appelé "théorème
de Cochran" ou
encore "théorème de Fisher-Cochran"
(dans le cas particulier d'échantillons gaussiens) et nous
donne donc une distribution pour les écarts-types empiriques
(dont la loi parente est une loi Normale).
En utilisant la valeur de l'écart-type démontrée
lors de notre étude da la loi du khi-deux nous avons donc:
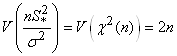 (7.129)
(7.129)
Mais n et 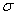 sont
imposés et sont donc considérés comme des constantes. Il vient
alors: sont
imposés et sont donc considérés comme des constantes. Il vient
alors:
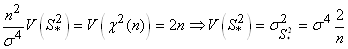 (7.130)
(7.130)
Et dès lors nous avons une expression de l'écart-type de l'écart-type
empirique si nous connaissons l'écart-type de la population:
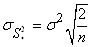 (7.131)
(7.131)
Mais nous avons démontré lors de notre étude des estimateurs
que:
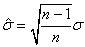 (7.132)
(7.132)
Dès lors il vient que:
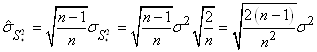 (7.133)
(7.133)
Il en découle donc la relation parfois importante
dans la pratique de l'estimateur de l'écart-type de.... l'écart-type:
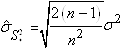 (7.134)
(7.134)
Rappelons que la population parente est dite "infinie" si
le tirage de l'échantillon est avec remise ou encore si la taille N de
la population parente est très supérieure à celle de n de
l'échantillon.
Remarques:
R1. En laboratoire, les  peuvent être
vues comme une classe d'individus d'un même produit étudié identiquement
par différentes équipes de recherche avec des instruments
de même
précision (écart-type de mesure identique). peuvent être
vues comme une classe d'individus d'un même produit étudié identiquement
par différentes équipes de recherche avec des instruments
de même
précision (écart-type de mesure identique).
R2.  est
la "variance interclasse" également
appelée "variance expliquée".
Donc elle donne la variance d'une mesure ayant eu lieu dans les
différents laboratoires. est
la "variance interclasse" également
appelée "variance expliquée".
Donc elle donne la variance d'une mesure ayant eu lieu dans les
différents laboratoires.
Ce qui est intéressant c'est qu'à partir du calcul de la loi
du Khi-deux en connaissant n et l'écart-type  il
est possible d'estimer cette variance (écart-type) interclasse. il
est possible d'estimer cette variance (écart-type) interclasse.
Pour voir que cette dernière propriété est une généralisation élémentaire
de la relation:
 (7.135)
(7.135)
il suffit de constater que la variable aléatoire  est
une somme de n carrés de N(0,1) indépendants les
uns des autres. Effectivement, rappelons qu'une variable aléatoire
centrée réduite (voir notre étude de la loi Normale) est donnée
par: est
une somme de n carrés de N(0,1) indépendants les
uns des autres. Effectivement, rappelons qu'une variable aléatoire
centrée réduite (voir notre étude de la loi Normale) est donnée
par:
 (7.136)
(7.136)
Dès lors:
 (7.137)
(7.137)
Or, puisque les variables aléatoires  sont
indépendantes et identiquement distribuées selon une loi
Normale, alors les variables aléatoires: sont
indépendantes et identiquement distribuées selon une loi
Normale, alors les variables aléatoires:
 (7.138)
(7.138)
sont aussi indépendantes et identiquement distribuées mais selon
une loi Normale centrée réduite.
Puisque:
 (7.139)
(7.139)
en réarrangeant nous obtenons:
 (7.140)
(7.140)
Donc sur la population de mesures, l'écart-type vrai suit
la relation donnée ci-dessus. Il est donc possible de faire
de l'inférence
statistique sur l'écart-type lorsque la moyenne théorique
est connue (...).
Puisque la fonction du Khi-deux n'est pas symétrique,
la seule possibilité pour faire l'inférence c'est
de faire appel au calcul numérique et nous noterons alors
l'intervalle de confiance à 95%
(par exemple...) de la manière suivante:
 (7.141)
(7.141)
Soit en notant  : :
 (7.142)
(7.142)
le dénominateur étant alors bien évidemment
le quantile de la loi du khi-2.
Cette relation est rarement utilisée dans la pratique car
la moyenne théorique n'est pas connue. Indiquons, aussi,
qu'afin d'éviter toute confusion, cette dernière
relation est souvent notée
sous la forme suivante:
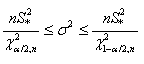 (7.143)
(7.143)
Voyons donc le cas le plus courant:
I.C. SUR LA VARIANCE AVEC MOYENNE EMPIRIQUE
Cherchons maintenant à faire de l'inférence statistique lorsque
la moyenne théorique de la population  n'est
pas connue. Pour cela, considérons maintenant la somme: n'est
pas connue. Pour cela, considérons maintenant la somme:
 (7.144)
(7.144)
où pour rappel est
la moyenne empirique (arithmétique) de l'échantillon: est
la moyenne empirique (arithmétique) de l'échantillon:
 (7.145)
(7.145)
En continuant le développement nous avons:

(7.146)
Or, nous avons démontré au début de ce chapitre que la somme
des écarts à la moyenne était nulle. Donc:

(7.147)
et reprenons l'estimateur sans biais de la loi Normale (nous
changeons de notation pour respecter les traditions et bien différencier
la moyenne empirique de la moyenne théorique):
 (7.148)
(7.148)
Dès lors:
 (7.149)
(7.149)
ou autrement écrit:
 (7.150)
(7.150)
Puisque le deuxième terme (au carré) suit une loi
Normale centrée
réduite aussi, alors si nous le supprimons nous obtenons
de par la propriété démontrée plus
haut de la loi du Khi-deux:
 (7.151)
(7.151)
Ces développements nous permettent cette fois-ci de faire aussi
de l'inférence sur la variance  d'une
loi d'une
loi  lorsque
les paramètres lorsque
les paramètres  et et  sont
tous les deux inconnus pour l'ensemble de la population. C'est
ce résultat qui nous donne, par exemple, l'intervalle de confiance: sont
tous les deux inconnus pour l'ensemble de la population. C'est
ce résultat qui nous donne, par exemple, l'intervalle de confiance:
 (7.152)
(7.152)
lorsque la moyenne théorique  est
donc inconnue. Et à aussi, pour éviter tout confusion, il est plutôt
d'usage d'écrire: est
donc inconnue. Et à aussi, pour éviter tout confusion, il est plutôt
d'usage d'écrire:
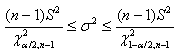 (7.153)
(7.153)
De la même manière que plus haut, nous pouvons calculer
l'écart-type
de l'écart-type et qui a une grande importance dans la pratique
de la finance:
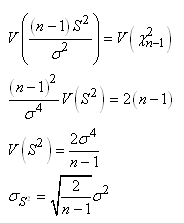 (7.154)
(7.154)
I.C. SUR LA MOYENNE AVEC VARIANCE EMPIRIQUE CONNUE
Nous avons démontré beaucoup plus haut que la loi de Student
provenait de la relation suivante:
 (7.155)
(7.155)
si Z et U sont des variables aléatoires indépendantes
et si Z suit une loi Normale centrée réduite N(0,1)
et U une loi du Khi-deux  tel
que: tel
que:
 (7.156)
(7.156)
et rappelons que la fonction de densité (distribution) est symétrique!
Voici une application très importante du résultat
ci-dessus:
Supposons que  constituent
un échantillon aléatoire de taille n issu de la loi constituent
un échantillon aléatoire de taille n issu de la loi  .
Alors nous pouvons déjà écrire que selon les développements faits
plus haut: .
Alors nous pouvons déjà écrire que selon les développements faits
plus haut:
 (7.157)
(7.157)
Et pour U qui suit une loi  ,
si nous posons ,
si nous posons  alors
selon les résultats obtenus plus haut: alors
selon les résultats obtenus plus haut:
 (7.158)
(7.158)
Nous avons alors après quelques simplifications triviales:
 (7.159)
(7.159)
Donc puisque:
 (7.160)
(7.160)
suit une loi de Student de paramètre k alors nous
obtenons le "independant one-sample t-test" (en
anglais) ou "test-T à 1 échantillon":
 (7.161)
(7.161)
qui suit aussi une loi de Student de paramètre n-1
et qui est très utilisé dans les laboratoires pour
les tests d'étalonnages.
Ce qui nous donne aussi après réarrangement:
 (7.162)
(7.162)
Ce qui nous permet de faire de l'inférence sur la moyenne  d'une
loi Normale d'écart-type théorique inconnu (sous-entendu
qu'il n'y a pas assez de valeurs expérimentales) mais dont
l'estimateur sans biais de l'écart-type
est connu. C'est ce résultat
qui nous donne l'intervalle de confiance: d'une
loi Normale d'écart-type théorique inconnu (sous-entendu
qu'il n'y a pas assez de valeurs expérimentales) mais dont
l'estimateur sans biais de l'écart-type
est connu. C'est ce résultat
qui nous donne l'intervalle de confiance:
 (7.163)
(7.163)
où nous retrouvons les mêmes indices que pour l'inférence
statistique sur la moyenne (espérance) d'une variable aléatoire
d'écart-type (théorique)
connu puisque la loi de Student tend asymptotiquement pour de grandes
valeurs de n vers une loi Normale. Ainsi, l'intervalle
précédent et l'intervalle suivant:
 (7.164)
(7.164)
donneront des valeurs très proches (à la troisième
décimale)
pour des grandeurs de n aux
alentours des 10'000 (dans la pratique on considère qu'à partir
de 100 c'est identique...).
Nous déduisons immédiatement par la
propriété de
stabilité de la loi du Khi-deux (démontrée
plus haut par le fait qu'elle découle de la loi Gamma) le
test suivant que nous retrouvons dans de très
nombreux logiciels de statistiques:
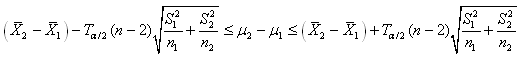 (7.165)
(7.165)
appelé "test-T (de
Student) bilatéral
sur la différence de deux moyennes" (rigoureusement...
sommer les degrés de liberté comme nous venons de le faire n'est
valable que si les deux variances sont égales et nous démontrerons
le cas général où les variances ne sont pas égales lors de la
démonstration du test de Welch plus loin).
Nous pouvons bien évidemment dès lors aussi
déterminer
la probabilité avec laquelle la moyenne est dedans ou en
dehors d'un certain intervalle... (l'une comme l'autre étant
beaucoup utilisées dans l'industrie).
Le lecteur pourra s'amuser à contrôler avec la version
française de Microsoft Excel 11.8346 que pour
un grand nombre de mesures n,
la loi de Student tend vers la loi Normale centrée réduite
en comparant les valeurs des deux fonctions ci-dessous:
=LOI.STUDENT.INVERSE.N(5%/2;n-1)
=LOI.NORMALE.STANDARD.INVERSE.N(5%/2)
Remarque: Le
résultat précédent fut obtenu par William
S. Gosset aux alentours de 1910. Gosset qui avait étudié la
mathématique et la chimie,
travaillait comme statisticien pour la brasserie Guinness en Angleterre. À l'époque,
on savait que si  sont
des variables aléatoires indépendantes et identiquement
distribuées
alors:
 (7.166)
(7.166)
Toutefois, dans les applications statistiques on s'intéressait
bien évidemment plutôt à la quantité:
 (7.167)
(7.167)
On se contentait alors de supposer que cette quantité suivait à peu
près une loi Normale centrée réduite ce qui
n'était pas une mauvaise
approximation comme le montre l'image ci-dessous ( ): ):

Figure: 7.2 - Comparaison entre la fonction de distribution Normale et celle de
Student
Suite à de nombreuses simulations, Gosset arriva à la conclusion
que cette approximation était valide seulement lorsque n est
suffisamment grand (donc cela lui donnait l'indication comme quoi
il devait y avoir quelque part derrière le théorème central limite).
Il décida de déterminer l'origine de la distribution et après avoir
suivi un cours de statistique avec Karl Pearson il obtint son fameux
résultat qu'il publia sous le pseudonyme de Student. Ainsi, on
appelle loi de Student la loi de probabilité qui aurait dû être
appelée la loi ou fonction de Gosset.
Signalons enfin que le test de Student est aussi très utilisé pour
identifier si des variations (progressions
ou l'inverse) de la moyenne des chiffres de deux
populations identiques sont statistiquement significatives. C'est-à-dire
que si la taille de deux échantillons dépendants
est identique alors nous pouvons créer le test suivant (nous
avons indiqué tous
les différents types d'écritures que l'on peut retrouver
dans la littérature et dans les nombreux logiciels implémentant
ce test):
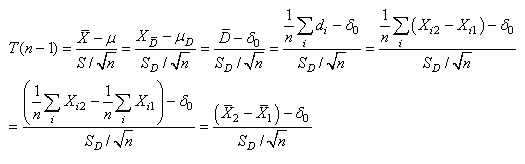 (7.168)
(7.168)
Avec:
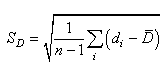 (7.169)
(7.169)
La relation antéprécédente
est donc très
utile pour comparer deux fois le même échantillon
dans des situations différentes de mesure (ventes avant
ou après
rabais d'un article par exemple). La relation antéprécédente
est appelée "test-T (de
Student) de deux moyennes d'échantillons appariés
(ou échantillons dépendants)" ou
plus simplement "test-T de Student pour
échantillons appariés".
Définition: Nous parlons
"d'échantillons appariés"
(par paires) si les échantillons de valeurs sont prises
2 fois sur les mêmes
individus (donc les valeurs des paires ne sont pas indépendantes,
contrairement à deux échantillons pris indépendamment).
TEST BINOMIAL EXACT
Il arrive fréquemment lors de mesures que l'on souhaite
comparer si deux échantillons de petite taille pris au hasard
(sans remise!) d'une population elle aussi petite... sont statistiquement
significativement différents ou non alors que l'on attendait
une égalité parfaite!
Nous cherchons donc un test adapté aux cas suivants:
- Savoir si un échantillon d'une population préfère
utiliser une technique de travail plutôt qu'une autre alors
que l'on s'attend à ce que la population utilise autant
l'une que l'autre
- Savoir si un échantillon d'une population a une caractéristique
prédominante parmi deux possibilités alors que l'on
s'attend à ce que la population soit parfaitement équilibrée
Avant d'aller plus en détails, rappelons qu'il faut être
extrêmement prudent quant à la manière d'obtenir
les deux échantillons. Il faut que l'expérience soit
non biaisée, cela signifie pour rappel, que le protocole
de tirage ne doit en aucun cas avantager l'une au l'autre des caractéristiques
de la population (si vous étudiez l'équilibre homme/femme
dans une population en attirant dans le sondage des personnes grâce à un
cadeau sous la forme de bijoux ou en appelant pandans les jours
ouvrés vous aurez alors un échantillon
biaisé... car vous aurez probablement naturellement plus
de femmes que d'hommes...).
Ceci étant dit, cette situation correspond donc à une
loi binomiale pour laquelle nous avons démontré plus
haut dans ce chapitre que la probabilité de k réussites
pour une population de taille N dont la probabilité de
réussite
est p (et la probabilité d'échec
q donc de 1 - p) était donnée par
la relation:
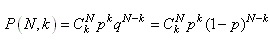 (7.170)
(7.170)
Dans le cas qui nous intéresse, nous avons donc 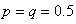 : :
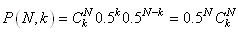 (7.171)
(7.171)
tout en
se rappelant que la distribution ne sera pas pour autant symétrique
et ce surtout si la taille N de la population est petite.
Si nous notons maintenant x le nombre de réussites
(considéré comme la taille du premier échantillon)
et y le
nombre d'échecs (considéré comme la taille
du deuxième échantillon), nous avons alors:
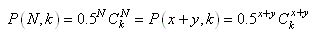 (7.172)
(7.172)
Ceci étant fait, pour construire le test et de par l'asymétrie
de la distribution, nous allons calculer la probabilité cumulée
que k soit plus petit que le x obtenu par l'expérience
et la sommer à la probabilité cumulée pour
que
k soit plus grand que le y obtenu par l'expérience
(ce qui correspond à la probabilité cumulée
des queues respectivement gauche et droite de la distribution).
Cette somme correspond donc à la probabilité:
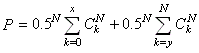 (7.173)
(7.173)
et cette dernière relation est appelée "test
binomial exact (bilatéral)".
Si la probabilité P obtenue pour la somme est
au-dessus d'une certaine probabilité cumulée fixée à l'avance,
nous dirons alors que la différence avec un échantillon
tiré au hasard dans une population parfaitement équilibrée
n'est pas statistiquement significative (en bilatéral...)
et respectivement si elle est en-dessous, la différence
sera donc statistiquement significative et nous rejetterons l'équilibre
supposé.
Ainsi,si:
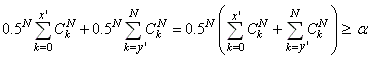 (7.174)
(7.174)
la différence par rapport à une population équilibrée
sera considérée comme non statistiquement significative.
Souvent on prendra au maximum 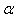 comme valant 5% (mais rarement en-dessous) ce
qui correspond donc à un intervalle de confiance de 95%.
comme valant 5% (mais rarement en-dessous) ce
qui correspond donc à un intervalle de confiance de 95%.
Malheureusement d'un logiciel de statistiques à l'autre
les paramètres demandés ou les résultats obtenus
ne seront pas nécessairement les mêmes (les tableurs
n'intègrent pas de fonction spécifique pour le test
binomial, il faudra souvent construire un tableau ou programmer
soi-même la fonction). Par exemple, certains logiciels calculent
systématiquement et imposent (ce qui est assez logique dans
un sens...):
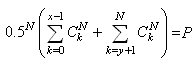 (7.175)
(7.175)
 Exemple: Exemple:
D'une petite population ayant deux caractéristiques x et
y particulières qui nous intéressaient et
pour laquelle nous nous attendions à avoir un parfait équilibre
tel que 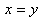 mais
nous avons en réalité obtenu mais
nous avons en réalité obtenu 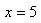 et et
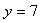 .
Nous souhaiterions faire le calcul avec Microsoft Excel 11.8346 pour savoir
si cette différence
est statistiquement significative ou non à un niveau de 5%? .
Nous souhaiterions faire le calcul avec Microsoft Excel 11.8346 pour savoir
si cette différence
est statistiquement significative ou non à un niveau de 5%?
Pour répondre à cette question, nous allons
donc calculer la probabilité cumulée:
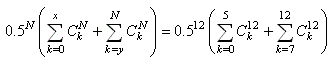 (7.176)
(7.176)
ce qui nous donne: 
Figure: 7.3 - Valeurs du calcul des coefficients binomiaux dans Microsoft Excel 11.8346
soit explicitement:

Figure: 7.4 - Formules du calcul des coefficients binomiaux dans Microsoft Excel 11.8346
donc la probabilité cumulée étant
de 0.774 (soit 77.4%) la différence
par rapport à une population équilibrée sera
considérée donc comme non statistiquement significative.
Remarque: Ce test est également
utilisé par la majorité
des logiciels de statistiques (comme Minitab) pour donner un intervalle
de confiance
de la conformité d'opinions par rapport à celle d'un
expert. C'est ce que nous appelons une étude R&R (reproductabilité & répétabilité)
par attributs (voir mon livre sur Minitab pour un exemple).
I.C. POUR UNE PROPORTION
Indiquons que certains statisticiens utilisent le fait que la
loi Normale découle de la loi de Poisson qui elle-même découle
de la loi Binomiale (nous l'avons démontré lorsque n tend
vers l'infini et que p et q sont du même ordre)
pour faire un intervalle de confiance dans le cadre de l'analyse
de proportions (très utilisé dans l'analyse
de la qualité dans les industries).
Pour voir cela, notons 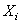 la
variable aléatoire définie par: la
variable aléatoire définie par:
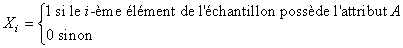 (7.177)
(7.177)
où l'attribut A peut être la propriété "défectueux" ou "non
défectueux" par exemple pour une analyse de pièces. Nous noterons k le
nombre de réussites de l'attribut A.
La variable aléatoire 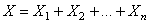 nous
l'avons démontré au début de ce chapitre, suit une loi Binomiale
de paramètres n et p avec les moments: nous
l'avons démontré au début de ce chapitre, suit une loi Binomiale
de paramètres n et p avec les moments:
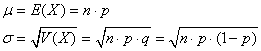 (7.178)
(7.178)
Ceci étant, nous ne connaissons pas la valeur vraie de p.
Nous allons donc utiliser l'estimateur de la loi Binomiale démontré plus
haut:
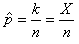 (7.179)
(7.179)
D'après les propriétés de l'espérance nous avons alors:
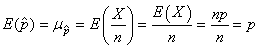 (7.180)
(7.180)
Et nous avons d'après les propriétés de la variance, la relation
suivante pour la variance de la moyenne empirique de la proportion:
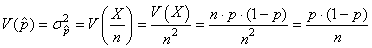 (7.181)
(7.181)
Ce qui nous amène alors à:
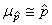 et et 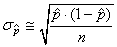 (7.182)
(7.182)
Maintenant rappelons enfin que nous avons démontré que
la loi Normale découlait de la loi Binomiale sous certaines
conditions (les praticiens admettent que c'est applicable tant
que n>50
et 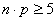 ).
Autrement dit, que la variable aléatoire X suivant
une loi Binomiale suit une loi Normale sous certaines conditions. Évidemment,
si X suit une loi Normale alors X/n aussi
(et donc ).
Autrement dit, que la variable aléatoire X suivant
une loi Binomiale suit une loi Normale sous certaines conditions. Évidemment,
si X suit une loi Normale alors X/n aussi
(et donc 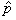 ...).
Dès lors nous pouvons centrer et réduire ...).
Dès lors nous pouvons centrer et réduire 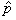 afin
qu'il se comporte comme la variable aléatoire Normale centrée
réduite notée Z: afin
qu'il se comporte comme la variable aléatoire Normale centrée
réduite notée Z:
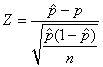 (7.183)
(7.183)
 Exemples: Exemples:
E1. Si 5% de la production annuelle d'une entreprise est défectueuse,
quelle est la probabilité qu'en prenant un échantillon
de 75 pièces
de la ligne de production que seulement 2% ou moins soit défectueux?
Nous avons dès lors avec:
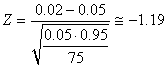 (7.184)
(7.184)
La probabilité cumulée correspondante à cette
valeur de la variable aléatoire est avec la version anglaise
de Microsoft Excel 11.8346:
=NORMSDIST(-1.19)=11.66%
Mais remarquez que nous n'avons pas 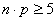 qui
est satisfait donc normalement il est exclu d'utiliser ce résultat. qui
est satisfait donc normalement il est exclu d'utiliser ce résultat.
E2. Dans son rapport de 1998, la banque J.P. Morgan a expliqué que
durant l'année 1998 ses pertes allèrent au-delà de
la Value at Risk (cf. chapitre d'Économie) 20 jours sur
les 252 jours ouvrés de l'année en se basant sur
une VaR temporelle de 95% (donc 5% des journées ouvrées
considérées comme à perte). Au seuil de 95%
est-ce de la malchance ou est-ce que le modèle de VaR utilisé était
mauvais?
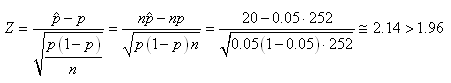 (7.185)
(7.185)
Donc c'était juste de la malchance.
Nous pouvons maintenant approximer l'intervalle de confiance pour
la proportion en se basant sur la loi Binomiale et son comportement
asymptotiquement
Normal dans les conditions démontrées lors de notre
introduction de la loi Normale tel que nous avons le "test Z à
une proportion" ou "test p à
une proportion" (dans le marketing appelée "test
A/B"):
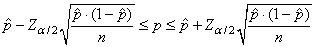 (7.186)
(7.186)
Avant de passer à un exemple, il est peut-être
utile de préciser au lecteur que cette approximation par
une loi Normale est très courante et que nous allons la
rencontrer encore de nombreuse fois dans les démonstrations
qui vont suivre. C'est tellement courant qu'on a même donné un
nom à cette méthode...:
la "méthode de Wald" (bon
en réalité il y a plusieurs méthodes
de Wald mais c'est la plus connue que nous utiliserons à chaque
fois).
 Exemple: Exemple:
Prenons 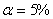 ,
nous avons alors: ,
nous avons alors:
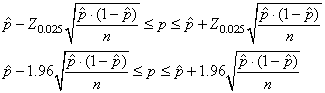 (7.187)
(7.187)
Sur une production de 300 éléments nous en avons trouvé 8 qui étaient
défectueux. Quel est donc l'intervalle de confiance?
Nous vérifions d'abord avec:
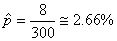 (7.188)
(7.188)
que:
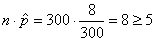 (7.189)
(7.189)
Donc il est acceptable d'utiliser l'intervalle de confiance par
la loi Normale. Nous avons dès lors:
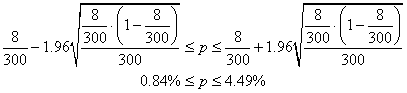 (7.190)
(7.190)
Pour clore ce sujet, nous pouvons évidemment nous intéresser
aussi au nombre d'individus (taille d'échantillon) qu'il faut avoir
pour satisfaire une certaine précision d'intervalle de confiance
(imposé)
en ayant un écart-type imposé.
Nous avons donc selon les hypothèses susmentionnées et dans l'acceptation
de l'approximation par une loi Normale que:
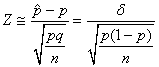 (7.191)
(7.191)
Et en procédant de manière identique aux développements effectués
plus haut avec la loi Normale, nous obtenons:
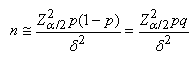 (7.192)
(7.192)
dont nous prenons évidemment normalement la valeur entière
supérieure
dans la pratique...
Einfin, faisons une petite excursion dans la théorie des
sondages/enquêtes par rapport à une relation que nous
retrouvont souvent dans la littérature spécialisée.
Si la taille de la population est petite telle que le système
ne peut pas
être
considéré avec
remise,
nous
utilisons
alors le facteur fpc démontré plus tôt.
Nous avons alors:
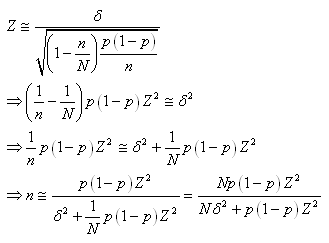 (7.193)
(7.193)
Soit:
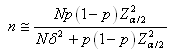 (7.194)
(7.194)
Une question qui revient souvent dans la pratique concerne le
fait de savoir s'il faut appliquer ce test en unilatéral
ou bilatéral.
Au fait il n'y a pas de réponse précise, tout dépend
de ce que nous cherchons à mettre en évidence.
Remarque: La taille de la population
mère pour les relations
développées plus haut n'entre pas en ligne
de compte dans le calcul des intervalles de confiance
ni dans celui de la taille de l'échantillon, et pour
cause, elle est considérée infinie. Il faut donc faire
attention
à ne pas avoir parfois des tailles d'échantillons qui
sont plus grandes que la population mère réelle possible...
 Exemple: Exemple:
Nous souhaiterions savoir le nombre d'individus (taille d'échantillon) à prendre
d'un lot de production sachant que la proportion de défectueux
est imposée à 30% avec une erreur tolérée
d'environ 5% entre la proportion réelle et empirique et
ce afin d'obtenir un intervalle de confiance à un niveau
de 95% du résultat:
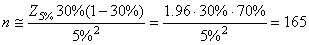 (7.195)
(7.195)
Remarque: La dernière relation est
très très souvent utilisée
en théorie des sondages (analyses pour des votations avec réponses
de type: Oui/Non) où parfois la taille de l'échantillon n est
imposée pour des raisons de coûts du sondage et dont nous cherchons à calculer
l'incertitude  et
parfois l'inverse (l'incertitude est imposée et donc nous cherchons à connaître
la taille de l'échantillon).
TEST DE L'ÉGALITÉ DE DEUX PROPORTIONS
Toujours dans le même contexte que l'approximation précédente
de la loi Binomiale par une loi Normale, l'industrie (en particulier
la biostatistique) est friande de comparer deux proportions de
deux populations différentes afin de savoir si elles sont
statistiquement égales
ou non (autrement dit: statistiquement significativement différentes
ou pas).
Dès lors rappelons que nous avons démontré la stabilité de la
loi Normale si deux variables aléatoires étaient indépendantes
et identiquement distribuées (selon une loi Normale donc!):
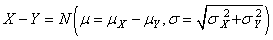 (7.196)
(7.196)
Dans le cadre des hypothèses susmentionnées il en est alors de
même approximativement pour la différence de deux proportions:
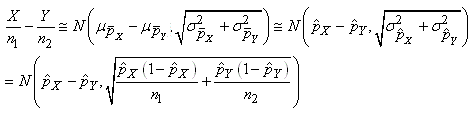 (7.197)
(7.197)
Remarque: Dans le domaine médical
où chacune des proportions
ci-dessus représente respectivement le risque avec traitement
et sans traitement nous parlons de " Risk
Difference" et
nous notons la différence  .
Si la différence est pare exemple de -5% cela signifie que nous
pouvons sauver 5% des patients. En plus, le corps médical introduit
aussi la notion de N.N.T. pour " Number
Needed to Treat" comme étant
le ration 1/ RD qui donne donc le nombre moyen de patient
à traiter pour éviter un événement indésirable. Ainsi avec 5% de
RD (en valeur absolue), nous devons traiter 20 patients
pour en sauver 1 statistiquement parlant.
Dès lors nous savons que cette nouvelle variable centrée réduite
suit une loi Normale selon:
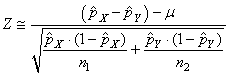 (7.198)
(7.198)
et comme nous cherchons à savoir la probabilité cumulée que l'espérance
théorique de la différence est nulle, cette dernière relation se
réduit alors dans ce cas à:
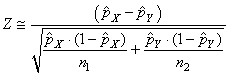 (7.199)
(7.199)
Évidemment nous pouvons aussi construire (comme toujours...)
un intervalle de confiance à partir de cette relation.
Remarque: Attention! Le test de la
différence
de deux proportions de deux échantillons différents
n'est évidemment pas le même que le test de la différence
de deux proportions dans un même échantillon (covariance
oublige puisque les deux proportions ne sont dès lors plus
indépendantes)! Dans le dernier cas nous utilisons le test
de McNemar (cf. chapitre de Méthodes Numériques)
Il semblerait cependant que cette dernière relation approximative
serait d'après l'expérience plus correcte en prenant pour dénominateur:
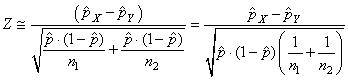 (7.200)
(7.200)
où 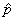 sera
pris comme le mélange de deux populations. C'est-à-dire: sera
pris comme le mélange de deux populations. C'est-à-dire:
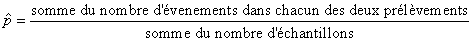 (7.201)
(7.201)
soit (en changeant la notations des indices des proportions
expérimentales):
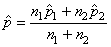 (7.202)
(7.202)
Ce test est aussi appelé "test
Z de l'égalité de deux proportions".
En médecine, on appelle cela le "test
des différences de risque" (en sous-entendant
que chaque proportion est une catégorie de population étudiée
par rapport
à un événement indésirable).
 Exemple: Exemple:
Dans le cadre d'un plan d'échantillonnage (cf.
chapitre de Génie
Industriel) nous avons prélevé sur un premier
lot de 50 individus, 48 en parfait états. Dans un second
lot de 30 individus, 26 étaient
en bon état.
Nous avons donc:
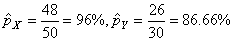 (7.203)
(7.203)
Nous souhaiterions donc savoir si la différence est statistiquement
significative avec une certitude de 95% ou simplement due au hasard.
Nous utilisons
alors:
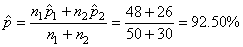 (7.204)
(7.204)
et:
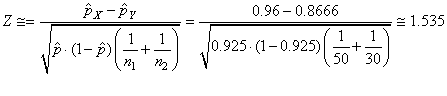 (7.205)
(7.205)
Ce qui correspond à une probabilité cumulée
en utilisant la version anglaise de Microsoft Excel 11.8346 de:
=NORMSDIST(1.535)=93.77%
Donc la différence est due au hasard (ceci dit c'est presque
in extremis...). Autrement dit, elle n'est pas statistiquement
significative sous les contraintes énoncées.
TEST DES SIGNES
Nous mesurons quelque chose sur un échantillon puis, plus tard,
nous mesurons la même chose sur ce même échantillon mais avec une
autre méthode (donc il s'agit donc d'échantillons
appariés!). Les deux classements ordonnées des mesures sont
comparés
et chaque observation est affectée d'un signe ("+" en
cas d'élévation dans
le classement, "" en cas de descente). Celles qui restent
au même niveau sont éliminées.
Selon l'hypothèse à tester, il y a autant de "+" que
de "",
c'est-à-dire
que la médiane de la distribution n'a pas bougé (cette affirmation
peut ne pas paraître évidente à la première
lecture il faut donc bien prendre du temps parfois pour réfléchir
là-dessus).
L'idée étant que pour chaque couple de valeurs, il n'y a que
deux signes possibles de variations, nous avons une chance sur
deux (50% de probabilité) que la différence soit positive ou négative.
Ce test est donc basé uniquement sur l'étude des signes des différences
observées
entre les paires d'individus, quelles que soient les valeurs de
ces différences.
Nous pouvons alors souhaiter contrôler deux hypothèses:
- L'inégalité des proportions de signes doit être statistiquement
significative. Donc l'un deux signes doit être en petit nombre
par rapport à l'autre,
ce qui correspond à un test unilatéral gauche (la probabilité cumulée
d'avoir ce petit nombre de signes doit être inférieur à un niveau  donné). donné).
- La proportion des deux signes doit être faiblement déséquilibrée
( ).
Il s'agit donc dans ce cas d'un test en bilatéral (c'est le cas
le plus courant) avec un certain niveau ).
Il s'agit donc dans ce cas d'un test en bilatéral (c'est le cas
le plus courant) avec un certain niveau 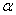 donné. donné.
Pour pouvoir créer un tel test, nous allons considérons l'apparition
des "+" et des "" comme un système de tirage
aléatoire binaire dont l'ordre des succès n'est pas pris en compte
(il s'agit donc d'une loi binomiale ou hypergéométrique) et avec
remise (ce qui élimine d'emblée la loi hypergéométrique qui n'est
pas symétrique et pose des problèmes d'utilisation dans la pratique...).
Pour considérer un tirage aléatoire avec remise (alors qu'on
ne fait pas réellement de remise), il faut que la population N soit
grande. Raison pour laquelle
le test des signes considère
que les valeurs appariées doivent être continues (ce qui permet
in extenso d'approcher la loi hypergéométrique
par la loi binomiale). Cependant certains logiciels de statistiques
utilisent la loi hypergéométrique pour des soucis
de précision.
Remarque: Il faut savoir que la majorité des
logiciels de statistiques, font implicitement l'hypothèse
lors de ce test que les données
sont continues et utilisent la loi binomiale.
 Exemple: Exemple:
Considérons deux séries de mesures avec deux méthodes différentes.
Nous souhaiterions tester l'hypothèse avec un niveau 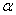 de
5% si la différence entre les deux méthodes est statistiquement
significative (nous nous attendons donc à une équilibre des signes).
Il s'agit donc d'un test des signes à deux échantillons
(sachant qu'il est possible de faire la même chose en comparant
les valeurs d'un seul et unique
échantillon à sa médiane). de
5% si la différence entre les deux méthodes est statistiquement
significative (nous nous attendons donc à une équilibre des signes).
Il s'agit donc d'un test des signes à deux échantillons
(sachant qu'il est possible de faire la même chose en comparant
les valeurs d'un seul et unique
échantillon à sa médiane).
20.4, 25.4, 25.6, 25.6, 26.6, 28.6, 28.7, 29,
29.8, 30.5, 30.9, 31.1
20.7, 26.3, 26.8, 28.1, 26.2, 27.3, 29.5, 32, 30.9, 32.3, 32.3,
31.7
Nous avons donc les différences:
-0.3, -0.9, -1.2, -2.5, 0.4, 1.3, -0.8, -3.0,
-1.1, -1.8, -1.4, -0.6
Soit:
, , , , +, +, , , , , ,
Bon il est déjà clair que le résultat va être le rejet de l'hypothèse
comme quoi il n'y pas de différence. Mais faisons quand même le
calcul. Comme le test est en bilatéral à un niveau de 5%, la probabilité cumulée
d'avoir obtenu au moins deux signes "+" ne doit pas être
inférieure à 2.5% et pas supérieure à 97.5% si l'on veut accepter
(ne pas rejeter) l'hypothèse comme quoi la différence n'est pas
statistiquement significative.
Nous avons alors:
 (7.206)
(7.206)
Soit avec la version française de Microsoft Excel 14.0.6123:
=LOI.BINOMIALE(2;12;0.5;1)=1.928%
ou si nous ne faisons pas d'approximation en étant
plus précis avec la loi hypergéométrique:
=LOI.HYPERGEOMETRIQUE.N(2;24/2;12;24;VRAI)=0.17%
ce qui n'est guère plus brillant...
Donc la probabilité cumulée est inférieure à 2.5%
et n'est de loin pas supérieure à 97.5%, nous rejetons l'hypothèse
comme quoi la différence n'est pas statistiquement significative.
Nous pourrions accepter l'hypothèse si nous prenions pour 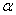 la
valeur: la
valeur:
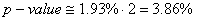 (7.207)
(7.207)
mais bon ce n'est pas le cas!
Enfin, pour terminer concernant ce test des signes (test de la
médiane), indiquons que certains logiciels de statistiques
proposent un
intervalle
de
confiance de la médiane basé sur la méthode
de calcul exposée précédemment (intervalle
de confiance d'une loi binomiale). Cependant, nous pensons qu'il
vaudrait mieux favoriser le bootstrapping comme
nous l'avons vu dans le chapitre de Méthodes Numériques,
nous nous abstiendrons donc de présenter cette technique
ici. De plus il est peu utile de préciser que certains font
un approximation en loi Normale (comme avec la majorité des
tests mais nous nous en abstiendrons dans le cas présent).
TEST DE LA MÉDIANE DE MOOD
Nous allons ici introduire un test qui a de multiples noms: "test
de la médiane", "test
de Mood", "test de la médiane
de Mood" ou encore "test
de la médiane de Westenberg-Mood" ou "test
de la médiane de Brown-Mood"...
Nous considérons deux échantillons indépendants 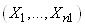 et et 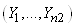 .
Nous supposons que .
Nous supposons que 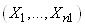 est
un échantillon indépendant et distribué selon une loi continue F et est
un échantillon indépendant et distribué selon une loi continue F et 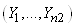 est
un échantillon indépendant et identiquement distribué d'une loi
continue G. est
un échantillon indépendant et identiquement distribué d'une loi
continue G.
Après regroupement des 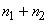 valeurs
des deux échantillons, valeurs
des deux échantillons, 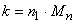 (la
notation n'est pas géniale car elle peut faire croire à une
multiplication mais bon...) est
le nombre d'observations (la
notation n'est pas géniale car elle peut faire croire à une
multiplication mais bon...) est
le nombre d'observations 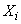 du
premier échantillon qui sont supérieures à la médiane
des du
premier échantillon qui sont supérieures à la médiane
des 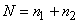 observations. observations.
Sous l'hypothèse nulle que les variables X et Y suivent
la même loi continue (c'est-à-dire G=F), la variable 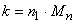 peut
prendre les valeurs peut
prendre les valeurs  selon
la loi hypergéométrique: selon
la loi hypergéométrique:
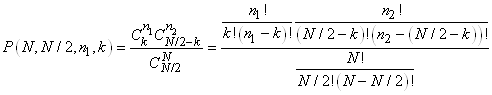 (7.208)
(7.208)
Dès lors, nous pouvons calculer la probabilité cumulée en unilatéral
d'avoir k. Le test de Mood est donc un test purement unilatéral.
 Exemple: Exemple:
Considérons les deux échantillons:
23.4, 24.4, 24.6, 24.9, 25.0, 26.2, 26.3, 26.8,
26.8, 26.9, 27.0, 27.6, 27.7
22.5, 22.9, 23.7, 24, 24.4, 24.5, 25.3, 26, 26.2,
26.4, 26.7, 26.9, 27.4
La médiane globale calculée avec Microsoft Excel 14.0.6123 est
de 26.10. Nous avons au total:
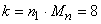 (7.209)
(7.209)
Il vient alors avec la version française de Microsoft Excel 14.0.6123:
=LOI.HYPERGEOMETRIQUE.N(8;26/2;13;26;VRAI)=94.24%
Donc à un seuil de 5%, nous ne rejettons pas l'hypothèse
nulle (mais bon étant proche de la limite c'est un peu périlleux
de conclure cela...). Si nous faisons le même calcul avec la loi
Binomiale nous obtenons:
=LOI.BINOMIALE.N(8;26/2;0.5;1)=86.65%
Mais bien évidemment ici l'approximation ne s'applique
pas puisque l'approximation par une loi binomiale est acceptable
dans la pratique que lorsque l'échantillon
est environ 10 fois plus petit que la population.
Remarque: Il existe malheureusement plusieurs versions du test
de Mood. Par exemple un logiciel comme Minitab compare à l'aide
d'une table de contingence... le contingent de valeurs au-dessus
ou en-dessous de la médiane et fait un simple test d'indépendance
du Khi-deux (test de Pearson) vu dans le chapitre de Méthodes Numériques.
TEST DE POISSON (1 ÉCHANTILLON)
Nous savons qu'un certain nombre d'événements rares suivent une
loi de Poisson. Nous pouvons alors nous permettre comme pour toute
autre loi, de calculer la probabilité cumulée dans un intervalle
donné (bilatéral ou unilatéral).
Donc, si nous avons une variable aléatoire discrète suivant une
loi de Poisson:
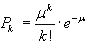 (7.210)
(7.210)
Nous avons alors en unilatéral droite à un certain niveau de confiance  ,
la valeur de n de k la plus proche satisfaisant la
condition: ,
la valeur de n de k la plus proche satisfaisant la
condition:
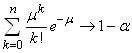 (7.211)
(7.211)
Donc pour trouver la valeur de n (entier strictement positif
ou nul) il faudrait inverser la somme, ce qui est peu... pratique
(raison pour laquelle aucun tableur à ce jour ne propose de fonction
pour la loi de Poisson inverse).
Maintenant, rappelons que nous avons vu dans le chapitre de Suites
Et Séries, la série de Taylor (Maclaurin) avec reste intégral à l'ordre n-1
autour de 0 jusqu'à 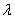 suivante: suivante:
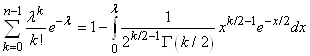 (7.212)
(7.212)
Résultat que nous avions également donné sous la forme de fonctions
pour la version française de Microsoft Excel 14.0.6123 pour que le lecteur
puisse vérifier
cette équivalence:
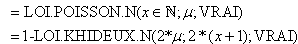 (7.213)
(7.213)
Il vient alors que dans les tableurs, nous pouvons utiliser la
loi du Khi-deux inverse pour calculer l'inverse de la loi de Poisson
avec cette fois cependant une petite nuance: le résultat ne donnera
pas nécessairement un nombre entier.
Si par exemple nous prenons (toujours avec la version française
de Microsoft Excel 14.0.6123):
=1-LOI.KHIDEUX.N(2*20;2*(15+1);VRAI)=0.156513135
(7.214)
La question est alors de trouver l'écriture pour l'inverse...
Celle-ci est alors donnée par (on divise par deux pour tomber
pile poile sur la moyenne qui est donc la valeur qui nous intéresse):
=KHIDEUX.INVERSE(1-0.156513135;2*(15+1))/2=15.53194258
(7.215)
Finalement, l'écriture de l'inverse est assez naturelle. Ainsi,
le "test de Poisson à 1 échantillon" à un
niveau  donné en
unilatéral droite peut s'écrire: donné en
unilatéral droite peut s'écrire:
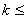 KHIDEUX.INVERSE(1-alpha;2*(nombre
de mesures+1))/2
(7.216) KHIDEUX.INVERSE(1-alpha;2*(nombre
de mesures+1))/2
(7.216)
Soit formellement:
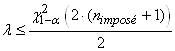 (7.217)
(7.217)
Attention cependant à une chose! Il semblerait que certains logiciels
de statistiques approximent parfois un peu abusivement la loi de
Poisson par une loi Normale. Dès lors, l'intervalle unilatéral
se calcule à partir de:
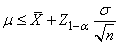 (7.218)
(7.218)
Mais avec la loi de Poisson, nous avons:
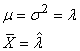 (7.219)
(7.219)
Il vient alors:
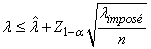 (7.220)
(7.220)
 Exemple: Exemple:
Une société fabrique des télévisions en quantité constante et
a mesuré le nombre d'appareils défectueux produits chaque trimestre
pendant les dix dernières années (donc 4 fois 10 mesures). La direction
décide que le nombre maximum acceptable d'unités défectueuses est
de 20 par trimestre et souhaite déterminer si l'usine satisfait à ces
exigences (sous l'hypothèse que la distribution des défectueux
suive une loi de Poisson) à un niveau de confiance de 5%.
Les 40 mesures nous donnent une moyenne de:
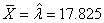 (7.221)
(7.221)
Nous avons alors avec l'approximation grossière:
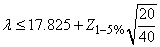 (7.222)
(7.222)
Soit dans un tableur comme la version française de Microsoft Excel 14.0.6123:
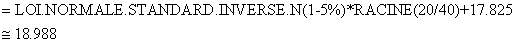 (7.223)
(7.223)
ou:
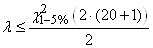 (7.224)
(7.224)
Soit dans un tableur comme la version française de Microsoft Excel 11.8346:
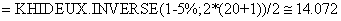 (7.225)
(7.225)
Dans les deux cas, nous sommes en-dessous de la moyenne imposée
de 20 (donc on rejette l'hypothèse nulle comme quoi le nombre de
défauts est supérieur ou égal à 20). Bien évidemment, il est possible
pour chacune des méthodes de déterminer quelle devrait être la
probabilité cumulée (niveau de confiance) qui nous amène à la limite
des 20 (donc la p-value en d'autres termes sur laquelle
nous reviendrons plus loin). Avec la première
méthode (approximation normale), la p-value est de 0.104%.
Évidemment, dans le cas bilatéral, nous avons:
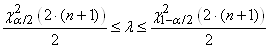 (7.226)
(7.226)
 Exemple: Exemple:
Une compagnie d'aviation a eu 2 deux crashs en 1'000'000 de vols
(événement très rare). Quelle est l'intervalle de confiance en
bilatéral à 95% sachant qu'au niveau mondial le nombre d'accident
par millions est de 0.4.
Nous avons alors:
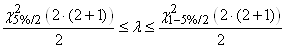 (7.227)
(7.227)
Soit pour la borne supérieure avec un tableur comme la version
française de Microsoft Excel 11.8346:
=LOI.KHIDEUX.INVERSE(1-5%/2;2*(2+1))/2=7.224
(7.228)
et pour la borne inférieure:
=LOI.KHIDEUX.INVERSE(1-5%/2;2*(2+1))/2=0.618
(7.229)
Donc statistiquement, cette compagnie est moins sûre
que l'ensemble des compagnies.
TEST DE POISSON (2 ÉCHANTILLONS)
Nous venons de voir que:
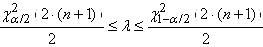 (7.230)
(7.230)
Or, en suivant le même raisonnement que celui qui nous a amené à construire
le test de comparaison des moyennes suivant:
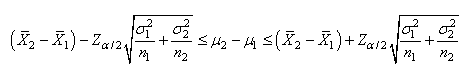 (7.231)
(7.231)
ou son équivalent avec la loi de Student quand l'écart-type vrai
n'est pas connu et en utilisant le fait que nous avons démontré que
la loi de Poisson est stable par l'addition (et donc aussi par
la soustraction), que la loi de Gamma était aussi stable par l'addition
(et donc aussi par la soustraction) et la loi du Khi-deux aussi
puisque ce n'est qu'un cas particulier de la loi Gamma. Nous aurions
peut-être tendance à écrire un peu une généralisation logique
de ce que nous avons vu juste plus haut:
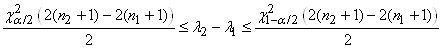 (7.232)
(7.232)
Et au fait cela constitue un piège selon certains praticiens...
Car la loi du Khi-deux a un support qui est défini comme étant
strictement positif et l'intervalle de confiance peut naturellement
avoir la
borne
de
gauche qui est
négative (... O_o). Une solution consiste alors à utiliser le test de la
différence de deux proportions que nous avons déjà étudié plus
haut:
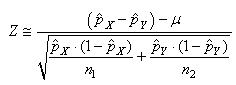 (7.233)
(7.233)
À condition bien évidemment que les conditions permettant d'approcher
le test par une loi Normale soient satisfaites (les proportions
doivent être inférieures typiquement à 0.1 et les n supérieurs à 50).
Certains logiciels semblent avoir implémenté
cette dernière
méthode (avec laquelle je ne suis pas forcément
d'accord).
 Exemple: Exemple:
Une compagnie d'aviation a eu 2 deux crashs en 1'000'000 de vols
(événement très rare). Une autre compagnie a eu 3 crashs en 1'200'000
vols. Quel est l'intervalle de confiance en bilatéral à 95% en
supposant que la différence est nulle.
Les proportions sont alors respectivement:
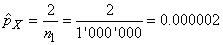 et et 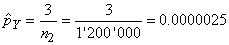 (7.234)
(7.234)
Notons:
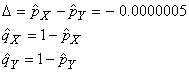 (7.235)
(7.235)
Nous avons alors:
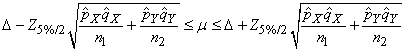 (7.236)
(7.236)
ce qui donne un intervalle de confiance pour la différence de
proportion théorique attendue:
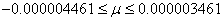 (7.237)
(7.237)
et donc comme -0.0000005 est dans cet intervalle, nous
acceptons l'hypothèse comme quoi la différence des proportions
n'est pas statistiquement significative au seuil de 5%.
Ou en prenant l'expression non approximée, nous avons (avec la
même conclusion):
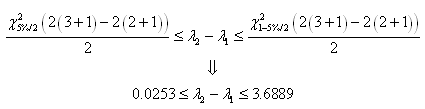 (7.238)
(7.238)
Donc pour résumer un peu les convergences de lois dans
tous ces différents
tests et intervalles que nous avons vu jusqu'à maintenant, nous
proposons au lecteur le schéma
suivant qui clarifiera peut-être plus ou moins bien les choses:
 Figure: 7.5 - Convergence des différentes lois usuelles en inférence statistique élémentaire
Figure: 7.5 - Convergence des différentes lois usuelles en inférence statistique élémentaire
Et aussi ce tableau où toutes les relations
ont
été démontrées en détail plus
haut et certains déjà utilisées (d'autres le seront plus loin):
|
Statistique d'échantillonnage
|
Moyenne
de la statistique
|
Écart-type
de la statistique
|
|
Moyenne
(population infinie)
|

|

|
|
Moyenne
(population finie)
|

|

|
|
Proportion
(population finie)
|
p
|

|
|
Proportion
(population infinie)
|
p
|

|
|

(population infinie*)
|

|

|
Tableau: 7.1 - Tableau des statistiques d'échantillonnage démontrées
et utilisées en partie jusqu'à
maintenant
*: Pour autant que la population parente soit distribuée normalement.
INTERVALLE DE CONFIANCE/TOLÉRANCE/PRÉDICTION
Nous allons ici, afin d'éviter une confusion fréquente et avant
de passer à d'autres sujets plus complexes, comparer l'intervalle
de confiance, l'intervalle de tolérance (souvent appelé "intervalle
de fluctuation" dans certains programmes scolaires)
et enfin l'intervalle de prédiction.
Définitions:
D1. "L'intervalle de tolérance" (ou "intervalle
de fluctuation") est un intervalle contenant un certain
pourcentage (souvent 68.26, 95.44 ou 99.73% pour une distribution
Normale) des individus d'une population
de mesures.
D2."L'intervalle de confiance" pour
un échantillon de moyenne 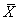 (ou
de proportion p) contient l'intervalle de valeur à un
niveau de confiance donné (souvent
90, 95 ou 99% dans le cas bilatéral) de l'espérance (ou
de proportion p) contient l'intervalle de valeur à un
niveau de confiance donné (souvent
90, 95 ou 99% dans le cas bilatéral) de l'espérance 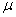 (moyenne
vraie) ou de la proportion de la population. (moyenne
vraie) ou de la proportion de la population.
D3. "L'intervalle de prédiction" permet
de déterminer un intervalle d'une valeur individuelle basée
sur la connaissance de la moyenne échantillonnale et de
l'écart-type de la population.
Un exemple valant mieux assez souvent mieux que mille mots,
prenons le cas où la moyenne et l'écart-type de prix de 49 DVD
sont:
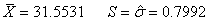 (7.239)
(7.239)
Nous avons alors:
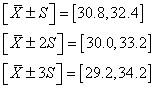 (7.240)
(7.240)
correspondant respectivement à des intervalles de tolérance selon
une loi Normale de 68.26, 95.44 et 99.73%.
Par contre, un intervalle de confiance à 95% basé sur la relation
démontrée plus haut:
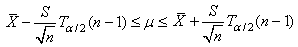 (7.241)
(7.241)
donne:
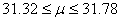 (7.242)
(7.242)
Donc 95% de probabilité cumulée que la moyenne vraie (espérance)
se trouve comprise entre 31.32 et 31.78.

Figure: 7.6 - Histogramme de l'échantillon des prix de 49 DVD
Maintenant passons à une notion qui curieusement est rarement
traitée
dans les ouvrages de statistiques. L'idée de l'intervalle de prédiction
est de plutôt que de s'intéresser à l'intervalle de confiance de
l'espérance basé sur une moyenne expérimentale, d'utiliser cette
moyenne expérimentale (échantillonnale) comme base pour
prévoir
l'intervalle d'une unique valeur (et non d'une moyenne!).
Nous allons donc nous intéresser à la différence entre la moyenne
et une valeur ponctuelle:
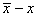 (7.243)
(7.243)
que nous supposerons proche de zéro (il vaut mieux pour avoir
un produit fiable et passer les tests d'autorisation des ventes...).
Concernant la variance, ce qui nous intéresse ce n'est plus simplement
l'écart-type de la moyenne mais l'écart-type de la différence...
et comme l'échantillon est indépendant de la valeur unique nous
avons:
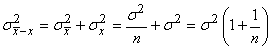 (7.244)
(7.244)
Donc nous pouvons écrire qu'en première approximation:
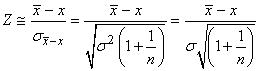 (7.245)
(7.245)
Et bien évidemment suite à ce que nous avons vu:
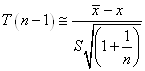 (7.246)
(7.246)
Et donc in extenso nous pouvons construire l'intervalle de prédiction:
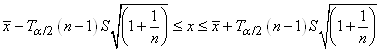 (7.247)
(7.247)
LOI FAIBLE DES GRANDS NOMBRES
Nous allons
maintenant nous attarder sur une relation très intéressante
en statistiques qui permet de dire pas mal de choses tout en
ayant peu de données et ce quelle que soit la
loi considérée (ce qui est pas mal quand même!).
C'est une propriété
très utilisée en simulation statistique par exemple
dans le cadre de l'utilisation de Monte-Carlo.
Soit une variable aléatoire à valeurs
dans  .
Alors nous allons démontrer la relation suivante appelée "inégalité de
Markov": .
Alors nous allons démontrer la relation suivante appelée "inégalité de
Markov":
 (7.248)
(7.248)
avec  dans
le contexte particulier des probabilités. dans
le contexte particulier des probabilités.
En d'autres termes, nous proposons
de démontrer
que la probabilité qu'une variable aléatoire soit plus grande ou égale
qu'une valeur  est
inférieure ou égale à son espérance divisée par la valeur considérée est
inférieure ou égale à son espérance divisée par la valeur considérée  et
ce quelle que soit la loi de distribution de la variable aléatoire
X! et
ce quelle que soit la loi de distribution de la variable aléatoire
X!
Démonstration:
Notons les valeurs de X par  ,
où ,
où  (c'est-à-dire
triées par ordre croissant) et posons (c'est-à-dire
triées par ordre croissant) et posons  .
Nous remarquons d'abord que l'inégalité est triviale
au cas où .
Nous remarquons d'abord que l'inégalité est triviale
au cas où .
Effectivement, comme X ne peut être compris qu'entre 0 et .
Effectivement, comme X ne peut être compris qu'entre 0 et
 par
définition alors la probabilité qu'il soit supérieur à par
définition alors la probabilité qu'il soit supérieur à  est
nulle. En d'autres termes: est
nulle. En d'autres termes:
 (7.249)
(7.249)
et X étant
positif, E(X) l'est
aussi, d'où l'inégalité pour ce cas particulier dans un premier
temps.
Sinon, nous avons  et
il existe alors un et
il existe alors un  tel
que tel
que  .
Donc: .
Donc:
 (7.250)
(7.250)
 C.Q.F.D. C.Q.F.D.
 Exemple: Exemple:
Nous supposons que le nombre
de pièces sortant
d'une usine donnée en l'espace d'une semaine est une variable aléatoire
d'espérance 50. Si nous souhaitons estimer la probabilité cumulée
que la production dépasse 75 pièces nous appliquerons
simplement:
 (7.251)
(7.251)
Considérons maintenant une sorte de
généralisation
de cette inégalité appelée "inégalité de
Bienaymé-Tchebychev" (abrégée "inégalité BT")
qui va nous permettre d'obtenir un résultat très
très très intéressant et important un
peu plus bas.
Considérons une variable aléatoire X réelle
(donc nous ne nous limitons pas au seul cas où elle est dans  ).
Alors nous allons démontrer
l'inégalité de
Bienaymé-Tchebychev suivante: ).
Alors nous allons démontrer
l'inégalité de
Bienaymé-Tchebychev suivante:
 (7.252)
(7.252)
qui exprime le fait que plus l'écart-type est petit, plus
la probabilité que la variable aléatoire X s'éloigne
de son espérance est faible.
Démonstration:
Nous obtenons cette inégalité en écrivant
d'abord:
 (7.253)
(7.253)
où le choix du carré va nous
servir pour une simplification future.
Puis en appliquant l'inégalité de Markov (comme
quoi c'est quand même utile...) à la variable aléatoire  avec avec  il
vient automatiquement: il
vient automatiquement:
 (7.254)
(7.254)
Ensuite, en utilisant la définition de la variance:
 (7.255)
(7.255)
Nous obtenons bien:
 (7.256)
(7.256)
 C.Q.F.D. C.Q.F.D.
Si nous posons:
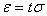 (7.257)
(7.257)
l'inégalité s'écrit aussi:
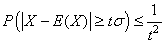 (7.258)
(7.258)
et exprime que la probabilité cumulée qu'afin que X s'éloigne
de son espérance de plus que t fois son écart-type,
est inférieure à 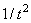 .
Il y a, en particulier, moins de 1 chance sur 9 pour que X s'éloigne
de son espérance de plus de trois fois l'écart-type.
C'est par ailleurs ce théorème qu'a utilisé le comité de Bâle pour
définir le facteur de correction de la Value At Risk utilisé en
finance (cf. chapitre d'Économie). .
Il y a, en particulier, moins de 1 chance sur 9 pour que X s'éloigne
de son espérance de plus de trois fois l'écart-type.
C'est par ailleurs ce théorème qu'a utilisé le comité de Bâle pour
définir le facteur de correction de la Value At Risk utilisé en
finance (cf. chapitre d'Économie).
 Exemple: Exemple:
Nous reprenons l'exemple où le nombre de pièces
sortant d'une usine donnée en l'espace d'une semaine est une variable
aléatoire d'espérance 50. Nous supposons en plus que la variance
de la production hebdomadaire est de 25. Nous cherchons à calculer
la probabilité que la production de la semaine prochaine soit comprise
entre 40 et 60 pièces.
Pour calculer ceci il faut d'abord
se souvenir que l'inégalité de BT est basée
en partie sur le terme  donc
nous avons: donc
nous avons:
 (7.259)
(7.259)
donc l'inégalité de BT nous permet bien de travailler
sur des intervalles égaux en valeur absolue ce qui s'écrit
aussi:
 (7.260)
(7.260)
Ensuite, ne reste plus qu'à appliquer simplement
l'inégalité numériquement:
 (7.261)
(7.261)
Les deux
dernières inégalités obtenues avant l'exemple
vont nous permettre d'obtenir une relation très importante
et puissante que nous appelons la "loi
faible des grands nombres" (L.F.G.N.) ou encore "théorème
de Khintchine".
Considérons une variable aléatoire X admettant
une variance et  une
suite de variables aléatoires indépendantes (donc non corrélées
deux-deux) de même loi que X et ayant toutes les mêmes espérances une
suite de variables aléatoires indépendantes (donc non corrélées
deux-deux) de même loi que X et ayant toutes les mêmes espérances  et
les mêmes écarts-types et
les mêmes écarts-types  . .
Ce que nous allons montrer est
que si nous mesurons une même quantité aléatoire  de
même loi au cours d'une suite d'expériences indépendantes
(alors dans ce cas, nous disons techniquement que la suite de
même loi au cours d'une suite d'expériences indépendantes
(alors dans ce cas, nous disons techniquement que la suite  de
variables aléatoires est définie sur le même espace
probabilisé),
alors la moyenne arithmétique des valeurs observées
va se stabiliser sur l'espérance de X quand le nombre
de mesures est infiniment élevé. de
variables aléatoires est définie sur le même espace
probabilisé),
alors la moyenne arithmétique des valeurs observées
va se stabiliser sur l'espérance de X quand le nombre
de mesures est infiniment élevé.
De manière formelle ceci s'exprime sous la forme:
 (7.262) (7.262)
lorsque  c'est
cela le résultat très important dont nous faisions
mention plus haut! L'estimateur empirique de la moyenne tend donc
pour toute
loi vers l'espérance vraie si n est grand! Donc
de par la même nous assurons que la moyenne empirique est
un estimateur convergent de l'espérance! Ce résultat
(assez intuitif) est parfois appelé "théorème
fondamental de Monte-Carlo"
car il est au centre du principe des simulations du même
nom (cf.
chapitre de Méthodes Numériques) qui ont une
importance cruciale dans l'étude des statistiques avancées. c'est
cela le résultat très important dont nous faisions
mention plus haut! L'estimateur empirique de la moyenne tend donc
pour toute
loi vers l'espérance vraie si n est grand! Donc
de par la même nous assurons que la moyenne empirique est
un estimateur convergent de l'espérance! Ce résultat
(assez intuitif) est parfois appelé "théorème
fondamental de Monte-Carlo"
car il est au centre du principe des simulations du même
nom (cf.
chapitre de Méthodes Numériques) qui ont une
importance cruciale dans l'étude des statistiques avancées.
Donc en d'autres termes la probabilité cumulée
que la différence entre la moyenne arithmétique et
l'espérance
des variables aléatoires observées soit comprise
dans un intervalle autour de la moyenne tend vers zéro quand
le nombre de variables aléatoires mesurées tend vers
l'infini (ce qui est finalement intuitif).
Ce résultat nous permet d'estimer l'espérance mathématique en
utilisant la moyenne empirique (arithmétique) calculée sur un très
grand nombre d'expériences.
Démonstration:
Nous utilisons l'inégalité de Bienaymé-Tchebychev
pour la variable aléatoire (cette relation s'interprète difficilement
mais permet d'avoir le résultat escompté):
 (7.263)
(7.263)
Et nous calculons d'abord en
utilisant les propriétés
mathématiques de l'espérance que nous avions démontrées plus
haut:
 (7.264)
(7.264)
et dans un deuxième temps en utilisant les propriétés
mathématiques de la variance aussi déjà démontrées
plus haut:
 (7.265)
(7.265)
et puisque nous avons supposé les variables
non corrélées entre elles alors la covariance est nulle dès
lors:
 (7.266)
(7.266)
Donc en injectant cela dans l'inégalité BT:
 (7.267)
(7.267)
nous avons alors:
 (7.268)
(7.268)
qui devient:
 (7.269)
(7.269)
et l'inégalité tend bien vers zéro quand n au
dénominateur tend vers l'infini.
 C.Q.F.D. C.Q.F.D.
Signalons que cette dernière relation est souvent notée dans
certains ouvrages et conformément à ce que nous avons
vu au début
de ce chapitre:
 (7.270)
(7.270)
ou encore:
 (7.271)
(7.271)
Donc, pour  : :
 (7.272)
(7.272)
FONCTION CARACTÉRISTIQUE
Avant de donner une démonstration à la manière
de l'ingénieur du théorème
central limite, introduisons d'abord le concept de "fonction
caractéristique" qui tient une place centrale
en statistiques.
D'abord, rappelons que la transformée de Fourier est donnée dans
sa version physicienne par (cf. chapitre
de Suites et Séries) la
relation:
 (7.273)
(7.273)
Rappelons que la transformation de Fourier est un analogue
de la théorie des séries de Fourier pour les fonctions
non périodiques, et permet de leur associer un spectre en
fréquences. Au facteur près, il s'agit d'une "transformée
de Laplace bilatérale" donnée par:
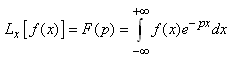 (7.274)
(7.274)
avec p qui est la variable complexe donnée dans
le cas présent par (la partie réelle est nulle puisque
la transformée de Fourier n'est que le cas particulier d'une
transformée
de Laplace dont la partie réelle de la variable est nulle:
dont faire une transformée de Fourier c'est faire une transformée
de Laplace sur l'axe des complexes uniquement):
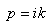 (7.275)
(7.275)
Nous souhaitons maintenant démontrer que si:
 alors alors  (7.276)
(7.276)
En d'autres termes, nous cherchons une expression simplifiée
de la transformée de Fourier de la dérivée de f(x).
Démonstration:
Nous partons donc de:
 (7.277)
(7.277)
Une intégration par parties donne:
 (7.278)
(7.278)
En imposant que, f tend vers zéro à l'infini, nous
avons alors:
 (7.279)
(7.279)
et:
 (7.280)
(7.280)
C'est le premier résultat dont nous avions besoin.
 C.Q.F.D. C.Q.F.D.
Maintenant, démontrons que si:
 alors alors  (7.281)
(7.281)
Démonstration:
Nous partons donc de:
 (7.282)
(7.282)
C'est le deuxième résultat dont nous avions besoin.
 C.Q.F.D. C.Q.F.D.
Maintenant effectuons le calcul de la transformée de Fourier
de la loi Normale centrée-réduite (ce choix n'est
pas innocent...):
 (7.283)
(7.283)
Nous savons que cette dernière relation est trivialement solution
de l'équation différentielle (ou bien elle vérifie):
 (7.284)
(7.284)
en prenant la transformée de Fourier des deux côté de l'égalité,
nous avons en utilisant les deux résultats précédents:
 alors alors  (7.285)
(7.285)
 alors alors 
Nous avons:
 (7.286)
(7.286)
Ou encore:
 (7.287)
(7.287)
Donc après intégration:
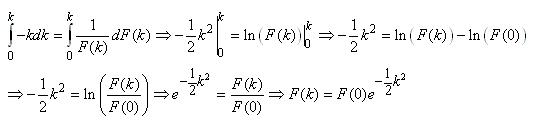 (7.288) (7.288)
Puisque:
 (7.289)
(7.289)
nous avons donc:
 (7.290)
(7.290)
Nous avons démontré lors de notre étude de la loi Normale
que:
 (7.291)
(7.291)
Donc:
 (7.292)
(7.292)
Nous avons alors (résultat important!):
 (7.293)
(7.293)
Introduisons maintenant la fonction caractéristique telle que
définie par les statisticiens:
 (7.294)
(7.294)
qui est un outil analytique important et puissant permettant
d'analyser une somme de variables aléatoires indépendantes.
De plus, cette fonction contient toutes les informations caractéristiques
de la variable aléatoire X.
Il s'agit
Remarque:
La notation n'est pas innocente puisque le E[...]
représente une espérance de la fonction de densité par
rapport à l'exponentielle
complexe.
Donc la fonction caractéristique de la variable aléatoire normale
centrée réduite de distribution:
 (7.295)
(7.295)
devient simple à déterminer car:
 (7.296)
(7.296)
Raison pour laquelle la fonction caractéristique de la
loi Normale centrée réduite est souvent assimilée à une
simple transformée
de Fourier.
Et grâce au résultat précédent:
 (7.297)
(7.297)
Donc:
 (7.298)
(7.298)
qui est le résultat dont nous avons besoin pour le théorème
central limite. Cette fonction caractéristique est égale, à une
constante près, à la densité de probabilité de
la loi. Nous disons alors que la fonction caractéristique
d'une gaussienne est gaussienne.
Mais avant cela, regardons d'un peu plus près cette fonction
caractéristique:
 (7.299)
(7.299)
En développement de Maclaurin nous avons (cf.
chapitre Suites et Séries) et en changeant un peu les notations:
 (7.300)
(7.300)
et en intervertissant la somme et l'intégrale, nous avons:
 (7.301)
(7.301)
Cette fonction caractéristique contient donc tous les moments
(terme général utilisé pour l'écart-type et l'espérance) de X.
THÉORÈME CENTRAL LIMITE
Le théorème central limite est un ensemble de résultats
du début du 20ème siècle sur la convergence
faible d'une suite de variables aléatoires en probabilité.
Intuitivement, d'après
ces résultats, toute somme (implicitement: la moyenne
de ses variables) de variables aléatoires indépendantes
et identiquement distribuées tend vers une certaine variable
aléatoire. Le résultat
le plus connu et le plus important est simplement appelé "théorème
central limite" qui concerne une somme de variables
aléatoires indépendantes avec variance existante dont le
nombre tend vers l'infini et c'est celui-ci que nous allons démontrer
de manière
heuristique ici.
Dans le cas le plus simple, considéré ci-dessous
pour la démonstration
du théorème, ces variables sont continues, indépendantes
et possèdent
la même moyenne et la même variance. Pour tenter d'obtenir un résultat
fini, il faut centrer cette somme en lui soustrayant sa moyenne
et la réduire en la divisant par son écart-type.
Sous des conditions assez larges, la loi de probabilité (de
la moyenne) converge alors vers une loi Normale centrée
réduite. L'omniprésence de la loi
Normale s'explique par le fait que de nombreux phénomènes
considérés
comme aléatoires sont dus à la superposition de causes nombreuses.
Ce théorème de probabilités possède donc une interprétation en
statistique mathématique. Cette dernière associe une loi de probabilité à une
population. Chaque élément extrait de la population est donc considéré comme
une variable aléatoire et, en réunissant un nombre n de
ces variables supposées indépendantes, nous obtenons un échantillon.
La somme de ces variables aléatoires divisée par n donne
une nouvelle variable nommée la moyenne empirique. Celle-ci, une
fois réduite, tend vers
une variable Normale réduite lorsque n tend vers l'infini
comme nous le savons.
Le théorème central limite nous dit à quoi il faut s'attendre
en matière de sommes de variables aléatoires indépendantes.
Mais qu'en est-il des produits? Eh bien, le logarithme d'un
produit (à facteurs strictement positifs) est la somme des logarithmes
des facteurs, de sorte que le logarithme d'un produit de variables
aléatoires (à valeurs strictement positives) tend vers une loi
Normale, ce qui entraîne une loi log-Normale pour le produit lui-même.
En elle-même, la convergence vers la loi Normale ("normalité
asymptotique") de nombreuses sommes de variables aléatoires
lorsque leur nombre tend vers l'infini n'intéresse que le
mathématicien.
Pour le praticien, il est intéressant
de s'arrêter un peu avant la limite: la somme d'un grand
nombre de ces variables est presque gaussienne, ce qui fournit
une approximation souvent plus facilement utilisable que la loi
exacte.
En s'éloignant encore plus de la théorie, on peut dire que bon
nombre de phénomènes naturels sont dus à la superposition de causes
nombreuses, plus ou moins indépendantes. Il en résulte que la loi
Normale les représente de manière raisonnablement efficace.
A l'inverse, on peut dire qu'aucun phénomène concret
n'est vraiment Gaussien car il ne peut dépasser certaines
limites, en particulier s'il est à valeurs positives.
Démonstration:
Soit  une
suite (échantillon) de variables aléatoires continues
(dans notre démonstration simplifiée...), indépendantes
(mesures de phénomènes
physiques ou mécaniques indépendants par exemple)
et identiquement distribuées, dont la moyenne une
suite (échantillon) de variables aléatoires continues
(dans notre démonstration simplifiée...), indépendantes
(mesures de phénomènes
physiques ou mécaniques indépendants par exemple)
et identiquement distribuées, dont la moyenne  et
l'écart-type et
l'écart-type  existent
(ce qui signifie que le théorème central limite fonctionne que
pour les phénomènes à variance finie!!!). existent
(ce qui signifie que le théorème central limite fonctionne que
pour les phénomènes à variance finie!!!).
Nous avons vu au début de ce chapitre que:
 (7.302)
(7.302)
sont les mêmes expressions d'une variable centrée réduite générée
à l'aide d'une suite de n variables aléatoires
identiquement distribuées qui par construction a donc une moyenne
nulle et une variance unitaire:
 et et  (7.303)
(7.303)
Développons la première forme de l'égalité antéprécédente
(les 2 sont de toute façon égales!):
 (7.304)
(7.304)
Maintenant utilisons la fonction caractéristique de la
loi Normale centrée-réduite (nous allégeons
par la même occasion l'écriture des estimateurs de
la moyenne et de l'écart-type):
 (7.305)
(7.305)
Comme les variables aléatoires  sont
indépendantes et identiquement distribuées, il vient: sont
indépendantes et identiquement distribuées, il vient:
 (7.306)
(7.306)
Un développement de Taylor (cf.
chapitre de Suites Et Séries) du terme entre accolades
donne au troisième
ordre (développement en série de Maclaurin de l'exponentielle):
 (7.307)
(7.307)
Finalement:

(7.308)
Posons:
 (7.309)
(7.309)
Nous avons alors:
 (7.310)
(7.310)
Et donc quand x tend vers l'infini (cf.
chapitre d'Analyse fonctionnelle):
 (7.311)
(7.311)
Nous retrouvons donc la fonction caractéristique de la loi Normale
centrée réduite!
En deux mots, le Théorème Central Limite (TCL) dit que pour de
grands échantillons, la somme centrée
et réduite de n variables
aléatoires identiquement distribuées suit
une loi Normale centrée et réduite. Et
donc nous avons in extenso pour la moyenne empirique:
 (7.312)
(7.312)
Malgré l'immensité de son champ d'applications, le TCL n'est
pas universel. Dans sa forme la plus simple, il impose en
particulier à la variable considérée d'avoir des moments du premier
et du deuxième ordre (moyenne et variance). Si tel n'est pas le
cas, il ne s'applique plus.
L'exemple le plus simple d'échec du TLC est donné par la distribution
de Cauchy, qui n'a ni moyenne, ni variance, et dont la moyenne
empirique a toujours la même distribution (Cauchy) quelle que soit
la taille de l'échantillon.
Maintenant, nous allons illustrer le théorème central limite
dans le cas d'une suite  de
variables aléatoires indépendantes discrètes suivant une loi de
Bernoulli de paramètre 1/2. de
variables aléatoires indépendantes discrètes suivant une loi de
Bernoulli de paramètre 1/2.
Nous pouvons imaginer que  représente
le résultat obtenu au n-ème lancé d'une pièce de monnaie
(en attribuant le nombre 1 pour pile et 0 pour face). Notons: représente
le résultat obtenu au n-ème lancé d'une pièce de monnaie
(en attribuant le nombre 1 pour pile et 0 pour face). Notons:
 (7.313)
(7.313)
la moyenne. Nous avons pour tout n bien évidemment:
  (7.314)
(7.314)
et donc:
  (7.315)
(7.315)
Après avoir centré et réduit  nous
obtenons: nous
obtenons:
 (7.316)
(7.316)
Notons  la
fonction de répartition de la loi Normale centrée réduite. la
fonction de répartition de la loi Normale centrée réduite.
Le théorème central limite nous dit que pour tout  : :
 (7.317)
(7.317)
A l'aide de Maple 4.00b nous avons tracé en bleu quelques graphiques
de la fonction:
 (7.318)
(7.318)
pour différentes valeurs de n. Nous avons représenté en
rouge la fonction  . .
 : :

Figure: 7.7 - Première approche de la loi de Bernoulli par le loi Normale selon
le
TCL
 : :

Figure: 7.8 - Deuxième approche de la loi de Bernoulli par le loi Normale selon
le
TCL


Figure: 7.9 - Troisième approche de la loi de Bernoulli par le loi Normale selon
le
TCL


Figure: 7.10 - Quatrième approche de la loi de Bernoulli par le loi Normale selon
le
TCL
Ces graphiques obtenus avec Maple 4.00b à l'aide des commandes suivantes:
> with(stats):
>
with(plots):
>
e1:=plot(Heaviside(t+1)*statevalf[dcdf,binomiald[1,0.5]](trunc((t+1)/2)),t=-2..2,y=0..1,color=blue):
>
e2:=plot(Heaviside(t+sqrt(2))*statevalf[dcdf,binomiald[2,0.5]](trunc((t*sqrt(2)+2)/2)),t=-sqrt(2)-1..sqrt(2)+1,y=0..1,color=blue):
>
e3:=plot(Heaviside(t+sqrt(5))*statevalf[dcdf,binomiald[5,0.5]](trunc((t*sqrt(5)+5)/2)),t=-sqrt(5)-1..sqrt(5)+1,y=0..1,color=blue):
>
e4:=plot(statevalf[cdf,normald](t),t=-5..5):
>
e5:=plot(Heaviside(t+sqrt(30))*statevalf[dcdf,binomiald[30,0.5]](trunc((t*sqrt(30)+30)/2)),t=-sqrt(30)-1..sqrt(30)+1,y=0..1,color=blue):
>
display({e1,e4});
>
display({e2,e4});
>
display({e4,e3});
>
display({e5,e4});
montrent
bien la convergence de  vers vers  . .
En fait nous remarquons que la convergence est carrément uniforme
ce qui est confirmé par le "théorème central limite de Moivre-Laplace":
Soit  une
suite de variables aléatoires indépendantes de même loi de Bernoulli
de paramètre p, une
suite de variables aléatoires indépendantes de même loi de Bernoulli
de paramètre p,  .
Alors: .
Alors:
 (7.319)
(7.319)
tend uniformément vers  sur sur  lorsque lorsque  . .
TESTS D'HYPOTHÈSE
ET D'ADÉQUATION
Lors de notre étude des intervalles de confiance, rappelons
que nous sommes arrivés aux quelques relations suivantes
(ce n'est que l'échantillon des plus importantes démontrées
plus haut!):
 (7.320)
(7.320)
et:
 (7.321)
(7.321)
et:  (7.322)
(7.322)
et enfin:  (7.323)
(7.323)
qui permettaient donc de faire de l'inférence
statistique en fonction de la connaissance ou non de la moyenne
ou de la variance vraie
sur la totalité ou sur un échantillon de la population.
En d'autres termes de savoir dans quelles bornes se situait un
moment (moyenne
ou variance) en fonction d'un certain niveau de confiance  imposé.
Nous avions vu que le deuxième intervalle ci-dessus ne peut être
que difficilement utilisé dans la pratique (suppose la moyenne
théorique
connue)
et nous lui préférons donc le troisième. imposé.
Nous avions vu que le deuxième intervalle ci-dessus ne peut être
que difficilement utilisé dans la pratique (suppose la moyenne
théorique
connue)
et nous lui préférons donc le troisième.
Nous allons également démontrer en
détails plus loin
les deux intervalles suivants:
 (7.324)
(7.324)
et:
 (7.325)
(7.325)
Le premier intervalle
ci-dessus ne peut être lui aussi que difficilement utilisé dans
la pratique (suppose la moyenne théorique connue) et
nous lui préférons donc le deuxième.
Définition: Lorsque nous cherchons à savoir
si nous pouvons faire confiance à la valeur d'une statistique
(moyenne, médiane, variance, coefficient de corrélation,
etc.) avec une certaine certitude, nous parlons de "test
d'hypothèse" et plus particulièrement
de "test
de conformité" (nous parlons de "test
d'adéquation"
quand il s'agit de vérifier que des mesures suivent bien
une loi donnée et non juste une statistique).
Les tests d'hypothèses sont destinés à vérifier
si un échantillon peut être considéré comme
extrait d'une population donnée ou représentatif
de cette population, vis-à-vis d'un paramètre comme
la moyenne, la variance ou la fréquence observée.
Ceci implique que la loi théorique du paramètre soit
connue au niveau de la population. Les tests d'hypothèses
ne sont pas faits pour démontrer l'hypothèse nulle
(exprimant généralement une égalité ou
une homogénéité entre différentes populations),
mais pour éventuellement la rejeter (dispons pour être
exact que le rejet est plus robuste). Au niveau de la communication
des tests statistiques un certain nombre de spécialistes recommandent:
1. De toujours communiquer la p-value avec
4 chiffres après la virgule (nous reviondrons plus loin
sur ce concept).
2. De ne jamais dire qu'un p-value faible
montre une amplitude importante de l'effet étudié car cela n'est
pas forcéement vrai (pour le vérifier il suffit de prendre un phénomène
de très petite amplitude sur une gros échantillon et la p-value
deviendra
toute de suite très petite par construction).
3. De toujours donner l'intervalle de confiance du
test qu'il soit unilatéral ou bilatéral.
4. De bien se garder de fixer un seuil de rejet au
test excepté si une norme ou législation l'impose
(dans ce dernier cas on précisera laquelle).
5. De ne jamais dire que le test est "démontré",
ou "significatif" ou même "statistiquement
significatif". Juste
dire que le résultat est "statistique" ou que
nous avons la "probabilité des données connaissant l'hypothèse
nulle" et c'est tout!
6. Si l'intérêt est de montrer l'hypothèse nulle
et que cette dernière n'est pas rejetée, étant donné souvent sa
puissance statistique faible, il faudra répéter l'expérience pour
conforter la conclusion.
7. Si l'intérêt est de rejeter l'hypothèse
nulle et que cela se vérifie, une bonne pratique scientifique
est de chercher des études supplémentaires qui mettraient en défaut
la conclusion.
8. S'il y a absence par exemple de différence
statistique entre deux valeurs, cela ne signfie pas pour autant
qu'il y ait présence
statistique d'équivalence. Il faut alors procéder à des "tests
d'équivalences".
9. La rejet de l'hypothèse nulle ne signifie
pas que le méchanisme du phénomène étudié a été mis
en évidence mais
indique juste pour rappel une information de taille sur les données
a posteriori.
10. Nous communiquons la puissance a posteriori du
test.
Bref, les études doivent être diffisusées en respectant
le principe de véracité, après avoir fait l'objet des vérifications
de rigueur, et doivent être exposées, décrites et présentées avec
impartialité. Il ne faut pas confondre résultats objectifs et spéculations.
Les conclusions doivent être l'expression le plus fidèle possible
du contenu des faites et des données.
Par exemple, si nous souhaitons savoir avec une
certaine confiance si une moyenne donnée d'un échantillon
de population est réaliste par rapport à la vraie moyenne théorique
inconnue, nous utiliserons le "test-Z" qui
est simplement:
 (7.326)
(7.326)
Maintenant rappelons que nous avons démontré que si nous avions
deux variables aléatoires de loi:
 (7.327)
(7.327)
alors la soustraction (différencier) des moyennes donne:
 (7.328)
(7.328)
Donc pour la différence de deux moyennes de variables aléatoires
provenant de deux échantillons de population nous obtenons directement:
 (7.329)
(7.329)
Nous pouvons alors adapter le test-Z sous la forme:
 (7.330)
(7.330)
La relation qui est très utile lorsque pour deux échantillons
de deux populations de données, nous voulons vérifier
s'il existe une différence statistiquement significative
des différences
des moyennes théoriques à un
niveau de confiance  fixé
et la probabilité associée pour avoir
cette différence: fixé
et la probabilité associée pour avoir
cette différence:
 (7.331)
(7.331)
Donc:
 (7.332)
(7.332)
Nous parlons du "test-Z de
la moyenne à deux échantillons" et il est beaucoup utilisé
dans l'industrie pour vérifier l'égalité de la moyenne de deux populations
de mesures.
Et si l'écart-type théorique n'est
pas connu, nous utiliserons le "test-T"
de Student (pas mal utilisé en pharmaco-économie)
démontré plus haut:
 (7.333)
(7.333)
Dans la même idée pour l'écart-type,
nous utiliserons le "test du Khi-deux
(de la variance)" aussi
déjà démontré plus haut:
 (7.334)
(7.334)
Et lorsque nous voulons tester l'égalité de
la variance de deux populations nous utilisons le "test-F"
de Fisher (démontré plus bas lors de notre étude
de l'analyse de la variance):
 (7.335)
(7.335)
Dans la pratique il faut avoir conscience que le
but d'un test est très très souvent de montrer que
l'effet est significatif. Il est alors d'usage de dire que le test
réussit
si l'hypothèse
nulle
est rejetée au profit de l'hypothèse alternative.
Lorsque le praticien sait que l'effet est significatif et pourtant
que son test échoue à rejeter l'hypothèse nulle on parle parfois
du "dilemne du non rejet de l'hypothèse
nulle". Comme nous le verrons un peu plus loin, l'idée est
alors de calculer à posteriori la puissance du test (celle-ci étant
alors appelée par certains logiciels comme SPSS: "puissance
observée") et d'adapter la taille de l'échantillon
en conséquence pour avoir une puissance acceptable selon la tradition
d'usage. ORIENTATION DU TEST D'HYPOTHÈSE
Le fait que nous obtenions l'ensemble des
valeurs satisfaisant à un testborné à droite
et (!) à gauche est
ce que nous appelons dans le cas général un "test
bilatéral" car il comprend le test unilatéral à gauche
et unilatéral à droite. Ainsi, tous les tests
susmentionnés
sont dans une forme bilatérale mais nous pourrions en faire
une utilisation unilatérale aussi! Nous utilisons un test
unilatéral
lorsque la différence attendue (ou à mettre en évidence)
ne peut aller que dans un sens (typiquement dans le cas des essais
cliniques
ou lors
d'un
action corrective de contrôle qualité en industrie
pour laquelle nous nous attendons à une amélioration
allant dans une unique direction). Les test unilatéraux
sont parfois nommés "test de
non-infériorité" (unilatéral
gauche) ou "test
de non-supériorité" (unilatéral
droite).
Ci-dessous, nous avons représenté
par exemple un test unilatéral à droite (car la région
de rejet est à droite et donc la probabilité cumulée est
unilatérale gauche) et un test bilatéral:
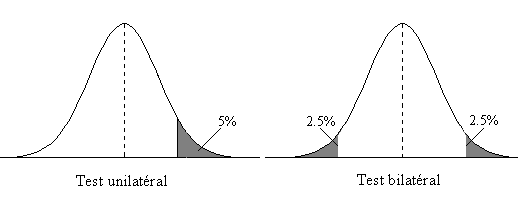
Figure: 7.11 - Illustration d'un test (ou intervalle de confiance) unilatéral
à droite et bilatéral
Nous pouvons également résumer la manière
de déterminer
la p-value (sur laquelle nous reviendrons plus loin en
détail) par le logigramme suivant:
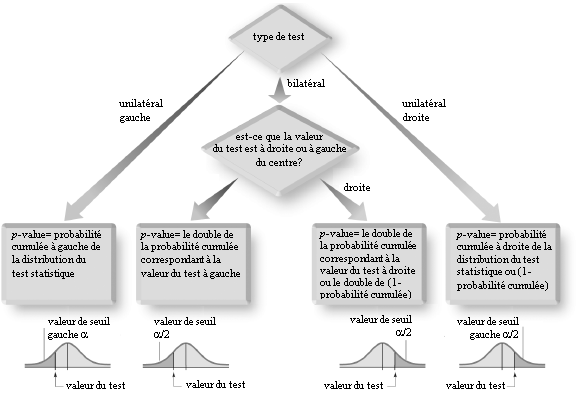
Figure: 7.12 - Figure de résumé pour déterminer la p-value
lors de tests paramétriques
à distribution symétrique
Signalons aussi que les tests d'hypothèses
sur l'écart-type
(variance), la moyenne ou la corrélation sont
appelés
des "tests
paramétriques" à l'inverse des tests
non paramétriques que nous verrons beaucoup plus loin.
Remarques:
R1. Il
existe également une autre définition du concept
de test paramétrique
et non-paramétrique (un peu différente car plus
précise)
à voir plus loin...
R2. Attention! Certains auteurs ou professeurs parlent parfois
de test "unilatéral à gauche" pour un "test
unilatéral à droite"...
Au fait il s'agit simplement d'un choix de vocabulaire. Si la
référence pédagogique n'est pas la zone
de rejet mais la zone d'acception, alors il est clair que les
concepts de droite et
gauche s'inversent...
Enfin, de nombreux logiciels calculent donc ce que
nous appelons la "p-value" qui
est le
risque calculé (probabilité)  qu'aurait
pu fixer le statisticien pour être à la limite entre
l'acceptation de l'hypothèse nulle et son rejet (rappelons
qu'un test qui réussit ne prouve rien). La p-value
est donc une valeur fondamentale
dans le
domaine car elle permet de chiffrer la vraisemblance
de l'hypothèse
nulle qu'aurait
pu fixer le statisticien pour être à la limite entre
l'acceptation de l'hypothèse nulle et son rejet (rappelons
qu'un test qui réussit ne prouve rien). La p-value
est donc une valeur fondamentale
dans le
domaine car elle permet de chiffrer la vraisemblance
de l'hypothèse
nulle 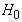 (acception
ou rejet). (acception
ou rejet).
Mais en toute rigueur la p-value est la
probabilité
conditionnelle (bayésienne), que nos données satisfont
l'hypothèse
nulle 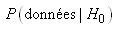 et
non la probabilité de l'hypothèse nulle connaissant
les données!
Même si la différence peut être faible comme
nous l'avons vu dans le chapitre de Probabilités, elle
n'en est pas moins non nulle! Donc la p-value en réalité ne
dit rien sur l'hyphothèse elle-même, mais elle donne
une information sur les données expérimentales. et
non la probabilité de l'hypothèse nulle connaissant
les données!
Même si la différence peut être faible comme
nous l'avons vu dans le chapitre de Probabilités, elle
n'en est pas moins non nulle! Donc la p-value en réalité ne
dit rien sur l'hyphothèse elle-même, mais elle donne
une information sur les données expérimentales.
Pour un test d'hypothèse, par exemple, le
5% de risque
 est
celui de rejeter l'hypothèse nulle est
celui de rejeter l'hypothèse nulle 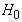 alors
même
qu'elle est vraie. Si le risque imposé/choisi est 5% et
que la p-value
calculée est inférieure (dans la majorité des
tests mais il faut
être prudent car ce n'est pas une généralité!!!),
le test échoue
(rejet de l'hypothèse nulle) en faveur d'une hypothèse
alternative notée alors
même
qu'elle est vraie. Si le risque imposé/choisi est 5% et
que la p-value
calculée est inférieure (dans la majorité des
tests mais il faut
être prudent car ce n'est pas une généralité!!!),
le test échoue
(rejet de l'hypothèse nulle) en faveur d'une hypothèse
alternative notée 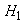 ou
parfois ou
parfois
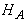 . .
L'hypothèse alternative a bien évidemment
elle-même
son propre risque que nous notons 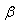 et
sa propre p-value. Donc lorsque l'hypothse nulle n'est
pas rejetée, le risque associé à cette décision
est un risque de deuxième espèce. Pour l'évaluer,
il faudrait donc calculer le puissance du test considéré. et
sa propre p-value. Donc lorsque l'hypothse nulle n'est
pas rejetée, le risque associé à cette décision
est un risque de deuxième espèce. Pour l'évaluer,
il faudrait donc calculer le puissance du test considéré.
Peut-être, pour mieux comprendre, voici une
illustration d'un cas particulier d'un test d'hypothèse
bilatéral
de la moyenne pour une variable aléatoire suivant typiquement
une loi Normale (en gros c'est le même principe pour tous
les tests...):
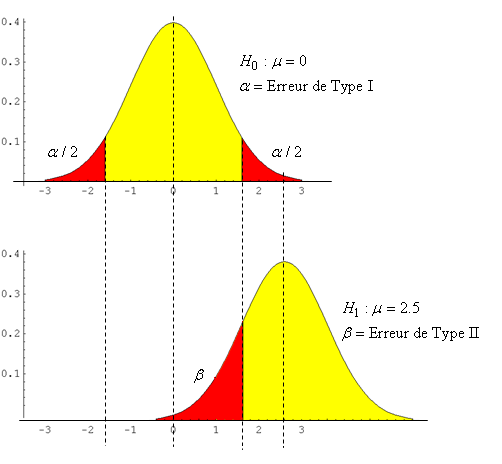
Figure: 7.13 - Hypothèse nulle et alternative d'un test bilatéral particulier
Ainsi, dans le cas présenté ci-dessus,
nous voyons mieux pourquoi l'hypothèse
nulle peut donc être acceptée ou rejetée en
faveur de l'hypothèse
alternative (qui est de même loi que l'hypothèse nulle
mais juste décalée) dépendant de la valeur
de référence
mesurée qui sera utilisée pour le test (en l'occurence
dans le cas particulier il s'agit de la moyenne arithmétique des
mesures).
Nous remarquons
aussi que la zone rouge de l'hypothèse
alternative, correspondant à la probabilité cumulée ,
est confondue en partie avec la partie jaune de l'hypothèse
nulle. Raison pour laquelle nous pouvons parfois accepter l'hypothèse
nulle à tort. Nous voyons cependant que plus ,
est confondue en partie avec la partie jaune de l'hypothèse
nulle. Raison pour laquelle nous pouvons parfois accepter l'hypothèse
nulle à tort. Nous voyons cependant que plus  serait
petit, plus l'hypothèse alternative serait donc éloignée
de la zone limite rouge de l'hypothèse nulle (cela correspondrait à une
translation vers la droite dans le cas présent) et moins
la probabilité
de faire une fausse conclusion est grande. Raison pour laquelle
nous parlons de "risque serait
petit, plus l'hypothèse alternative serait donc éloignée
de la zone limite rouge de l'hypothèse nulle (cela correspondrait à une
translation vers la droite dans le cas présent) et moins
la probabilité
de faire une fausse conclusion est grande. Raison pour laquelle
nous parlons de "risque  " car
plus celui-ci est petit, mieux c'est. In extenso, plus " car
plus celui-ci est petit, mieux c'est. In extenso, plus 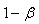 est
grand, moins il y a de risque de confondre l'hypothèse nulle
et alternative. Raison pour laquelle est
grand, moins il y a de risque de confondre l'hypothèse nulle
et alternative. Raison pour laquelle 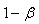 est
appelé "puissance du test" (voir
plus bas la section qui est consacrée à cette notion). est
appelé "puissance du test" (voir
plus bas la section qui est consacrée à cette notion).
Nous acceptons l'hypothèse nulle
si la p-value est plus grande que 5% (0.05). Au fait,
plus la p-value est grande, mieux c'est car l'intervalle
de confiance est de plus en plus petit. Si l'intervalle de confiance
vient à être énorme (très proche de
100%) car la p-value
est très petite alors l'analyse n'a plus vraiment de sens
physiquement parlant!
Ainsi, si la p-value est faible, c'est
qu'il faudrait prendre un risque faible de se tromper, donc accepter
dans presque tous les cas l'hypothèse testée...
Remarque:
Nous ne devrions
jamais dire que nous "acceptons" une hypothèse
ou encore qu'elle est "vraie" ou "fausse"
car ces termes sont trop forts et pourraient faire penser à une
preuve scientifique. Nous devrions dire si nous "rejetons"
ou "ne rejetons pas" l'hypothèse nulle et qu'elle
est éventuellement "correcte" ou
"non correcte".
Pour les test d'hypothèses bilatéraux, nous pouvons par exemple
dire que nous avons (ou n'avons pas) une différence significative
entre la valeur de référence
mesurée et la valeur attendue. Pour les tests unilatéraux, nous
pouvons dire que la valeur de référence mesurée est significativement
plus grande ou plus petite que la valeur attendue.
Par ailleurs si le lecteur a bien compris
la construction des tests d'hypothèses, le fait de rejeter
une hypothèse à tort ("Erreur
de Type I" ou "Erreur
de première espèce") est donc plus robuste
que de l'accepter à tort
("Erreur de type II" ou "Erreur
de deuxième
espèce").
Le lecteur remarquera aussi en s'aidant de la figure précédent
qu'un test unilatéral a une plus forte puissance qu'un
test unilatéral
(a même niveau de risque bien entendu!). Ainsi, une différence
non statistiquement significative en test bilatéral, peut
s'avérer statistiquement
significative en unilatéral.
Définitions:
D1. La probabilité  de
l'erreur de Type I (de première espèce/faux négatif)
est la probabilité de
rejet de l'hypothèse nulle alors qu'elle
est vraie. de
l'erreur de Type I (de première espèce/faux négatif)
est la probabilité de
rejet de l'hypothèse nulle alors qu'elle
est vraie.
D2. La probabilité 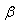 de
l'erreur de Type II (de deuxième espèce/faux positif)
est la probabilité de
maintien de l'hypothèse nulle alors qu'elle
est fausse. de
l'erreur de Type II (de deuxième espèce/faux positif)
est la probabilité de
maintien de l'hypothèse nulle alors qu'elle
est fausse.
Ainsi, un critère traditionnel de sélection de test est d'utiliser
le principe suivant: parmi tous les tests qui ont la même grandeur
de l'erreur de type I, choisir celui qui a la plus petite grandeur
de l'erreur de type II.
En général, la grandeur de l'erreur de type II augmente lorsque
celle de l'erreur de type I diminue. Nous ne pouvons pas minimiser
les deux erreurs à la fois. Pour cette raison, nous prenons souvent
une valeur donnée pour  ,
la grandeur de l'erreur de type I, et nous minimisons ,
la grandeur de l'erreur de type I, et nous minimisons 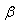 ,
la grandeur de l'erreur de type II. ,
la grandeur de l'erreur de type II.
Pour clore, voici les trois situations types de tests d'hypothèses
sur la statistique qu'est la moyenne dans le cadre d'une distribution
sous-jacente normale et dont l'espérance est dans ce cas
particulier supposée nulle et de variance unitaire (car
on peut très souvent ce ramener à ce cas particulier
en centrant et réduisant la variable aléatoire sous-jacente):
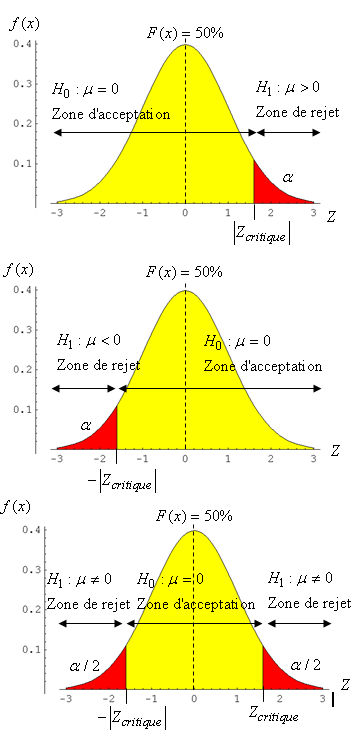
Figure: 7.14 - Les trois scénarios possibles d'un test d'hypothèse sur
la moyenne
Indiquons que cela n'a aucun sens (contrairement à ce que
nous pouvons parfois lire sur certains supports papier ou électronique)
d'avoir les hypothèses nulles suivantes dans le cas paticulier
représenté ci-dessus:
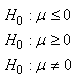 (7.336)
(7.336)
avec l'hypothèse alternative qui en découle automatiquement
(je ne l'ai pas écrite car c'est inutile). La raison en
est simple: comment pourriez-vous positioner votre
distribution Normale centrée réduite si l'espérance
n'est pas fixée...??? Raison
pour laquelle l'hypothèse nulle dans le cadre des tests
sur la moyenne (et d'un certain autre nombre de tests) est toujours
une
égalité!
Pour résumer, nous pouvons dire que si nous prenons une décision,
nous pouvons nous tromper et il vaut mieux éviter
de se tromper souvent. En clair, la probabilité de dire
une bêtise
doit être connue et de préférence petite.
pUISSANCE D'UN TEST
Lorsque l'effet est concrètement important, on imagine bien qu'il
faut moins d'observations pour le démontrer que lorsqu'il est petit...
mais combien au juste? A-t-on les moyens, en termes de nombre de
mesures, de démontrer ce que l'on cherche? Faut-il s'y prendre
autrement et changer le dispositif de son observation/expérimentation?
Pour étudier plus en détails la notion de "puissance de test"
que nous avons jusque là uniquement mentionnée,
rappelons la figure suivante déjà rencontrée juste un peu plus
haut:

Dans l'exemple particulier ci-dessus, nous allons donc rejeter
l'hypothèse
nulle si 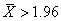 ou
si ou
si 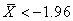 .
Imaginons que dans le cadre de l'hypothèse alternative, si nous
avons mesuré 2.5,
nous aurons comme puissance du test: .
Imaginons que dans le cadre de l'hypothèse alternative, si nous
avons mesuré 2.5,
nous aurons comme puissance du test:
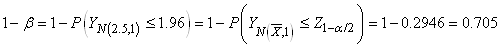 (7.337)
(7.337)
Donc le test est relativement puissant (dans la pratique, nous
considérons un test comme étant puissant si sa valeur est au-delà de
80%). Ainsi, nous remarquons que la puissance 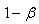 (a
posteriori!) est d'autant plus grande que la p-value sera
petite (et respectivement la puissance sera à posteriori
d'autant plus petite que la p-value
sera grande). Donc la puissance a posteriori est en
correspondance décroissante avec la p-value (dans
la pratique il est cependant un peu absurde de faire ces calculs
a posteriori). (a
posteriori!) est d'autant plus grande que la p-value sera
petite (et respectivement la puissance sera à posteriori
d'autant plus petite que la p-value
sera grande). Donc la puissance a posteriori est en
correspondance décroissante avec la p-value (dans
la pratique il est cependant un peu absurde de faire ces calculs
a posteriori).
PUISSANCE DU TEST Z À 1 ÉCHANTILLON
En toute généralité, dans le cas d'un test bilatéral, la relation
précédente s'écrira donc:
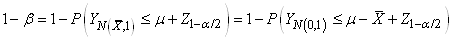 (7.338)
(7.338)
Si l'écart-type de la moyenne n'est pas été unitaire, nous avons:
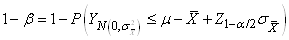 (7.339)
(7.339)
Il vient donc:
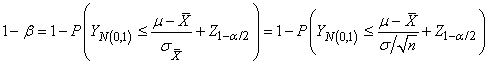 (7.340)
(7.340)
autrement écrit:
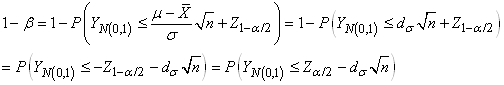 (7.341)
(7.341)
C'est sous cette forme que nous retrouvons la puissance d'un test
bilatéral de la moyenne (puissance Z à 1 échantillon):
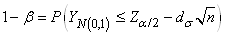 (7.342)
(7.342)
où d est parfois appelé la "taille
d'effet" et
est donc donné par:
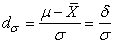 (7.343)
(7.343)
et  est
nommé la "différence"! est
nommé la "différence"!
Il va de soit que si la variance vraie n'est pas connue, il faut
alors remplacer la loi Normale par la loi de Student tel que:
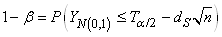 (7.344)
(7.344)
avec:
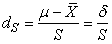 (7.345)
(7.345)
Remarque: Attention à un petit piège courant! Le développement
ci-dessus correspond à un  qui
est donc négatif relativement à l'exemple de départ! La relation
est un peu différente dans le cas où  est
positif mais cela n'a aucune importance car la puissance du test
est identique valeur absolue!
Pour avoir la taille de l'échantillon c'est assez simple. Nous
avons:
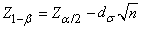 (7.346)
(7.346)
et donc en bilatéral:
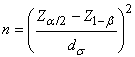 (7.347)
(7.347)
où nous voyons que si la puissance du test est imposée
comme étant
égale à 50%, ayant Z qui vaut alors 0 nous
retombons (!)sur la relation de l'effectif de l'échantillon
pour loi Normale démontrée bien plus haut:
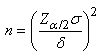 (7.348)
(7.348)
Signalons aussi que nous retrouvons parfois dans la littérature
la relation antéprécédente sous la forme suivante:
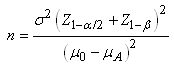 (7.349)
(7.349)
Évidemement nous pouvons fixer d'autres paramètres pour déterminer
la valeur de la variable restante. Nous pourrions par exemple chercher
la valeur de la puissance du test en imposant l'écart-type, la
taille de l'échantillon et le niveau de confiance, etc.
Un lecteur nous a proposé une maniètre très élégante de retrouver
le même résultat avec beaucoup moins de développements... Effectivement,
il suffit de voir sur la figure précédente que nous avons:
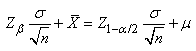 (7.350)
(7.350)
Donc nous tirons immédiatement une relation équivalement
aux deux précédentes (qui donne bien évidemment le même résultat
numérique):
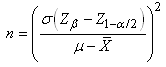 (7.351)
(7.351)
Remarque: Le lecteur attentif aura
peut-être remarqué
que nous avons supposé dans les développements qui
précédent que
l'écart-type de la moyenne vraie et aternative (estimée)
est implicitement supposée être la même... Dans
la pratique cela est presque tout le temps le cas, raison pour
laquelle les quasi totalité des
logiciels de statistiques ne demandent qu'un seul écart-type
pour le calcul de la puissance du test Z à 1 échantillon.
Cependant, dans certains rares logiciels universitaires, on demande
l'écart-type
des deux moyennes. Mais dès lors les développements ci-dessus
sont différents.
Une analyse de puissance peut avoir plusieurs facettes:
1. Nous connaissons le niveau du test, la taille d'échantillon
et la taille d'effet (implicitement la différence) et nous cherchons à calculer
la puissance. Ceci permet de voir si notre dispositif expérimental
est bien calibré.
2. Nous connaissons la puissance voulue, le niveau du test et
la taille d'effet à détecter. Nous cherchons alors à calculer la
taille d'échantillon nécessaire pour monter un dispositif expérimental
efficace.
3. Nous connaissons la puissance voulue, le niveau du test et
la taille d'échantillon et nous cherchons à vérifier qu'elle taille
d'effet nous pouvons espérer mettre en évidence.
Sauf exception, nous considèrerons qu'il est inutile de
montrer un test si la puissance escomptée est inférieure à 80%.
Cette puissance correspond à une probabilité de 80%
de ne pas rejeter l'hypothèse nulle à tort, ou, ce
qui revient au même de 20% d'erreur de type II.
Évidemment, il est possible de faire le même raisonnement (analytiquement
quand c'est possible, sinon numériquement) avec absolument
TOUS les tests d'hypothèses que nous avons vus jusqu'à maintenant.
Donc au même titre qu'il y a un peu plus d'une centaine de tests
d'hypothèses
dans le domaine des statistiques comme nous l'avons déjà mentionné...
il est évident que nous n'allons pas nous... amuser... à faire
les mêmes développements pour tous ces tests mais seulement pour
les grands classiques. Tant que nous avons des ordinateurs à notre
disposition avec les algorithmes intégrés
par des informaticiens/scientifiques, nous pouvons nous passer
de refaire tous les développements qui n'apporteraient pas grand
chose. Par ailleurs, la majorité des logiciels comportement des
outils pour calculer la puissance de 5 à 10 tests le plus souvent.
Remarque: Nous ne traiterons pas des
tests statistiques paramétriques de détection des
valeurs abérrantes sur ce site comme le test Q de Dixon
ou de Grubb pour la simple raison qu'ils ont une origine trop
empirique et qu'ils n'ont aucun intérêt analytiquement
parlant. Par contre, si des lecteurs insistent, nous pourrons
mettre les détails sur ces tests avec les algorithmes
détaillés de calcul des valeurs critiques en utilisant
un simple tableur et la technique de Monte-Carlo pour n'importe
la distribution de leur votre choix (mais pas uniquement selon
la loi Normale contrairement à ce qui est écrit
dans la majorité des livres).
puissance du test p À 1 ET 2 ÉCHANTILLONS
De même que l'intervalle de confiance de la loi Normale
avec écart-type théorique connu (c'est-à-dire
sur toute la population), nous pouvons déterminer le nombre
d'individus (taille d'échantillon) si nous souhaitons imposer
une puissance au test de la proportion à 1 échantillon
étudié plus haut. Pour cela, nous utilisons la même
technique que pour la puissance du test Z. Nous écrivons
alors dans un premier temps:
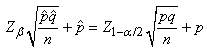 (7.352)
(7.352)
D'où nous déduisons:
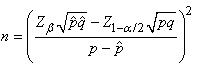 (7.353)
(7.353)
Donc si la puissance est de 50%, nous retrouvons
bien:
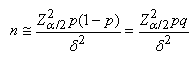 (7.354)
(7.354)
Pour la puissance du test de la différence de deux proportions
(test de la proportion à deux échantillons) dans
l'objectif de déterminer
la taille de l'échantillon
nous sommes obligés de poser  .
Dés lors, les développements obtenus lors de l'étude du test de
la différence de deux proportions s'écrivent: .
Dés lors, les développements obtenus lors de l'étude du test de
la différence de deux proportions s'écrivent:
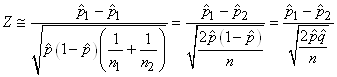 (7.355)
(7.355)
avec:
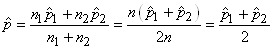 (7.356)
(7.356)
De la même manière que nous l'avons fait pour le test Z et
le test p à 1 échantillon, nous avons:
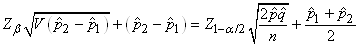 (7.357)
(7.357)
Soit:
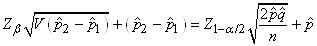 (7.358)
(7.358)
Ce qui revient donc à supposer que la différence vraie des deux
proportions est la moyenne (ce qui est discutable...).
Mais nous avons aussi (comme les échantillons sont indépendants
de par la propriété de la variance):
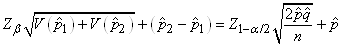 (7.359)
(7.359)
Soit:
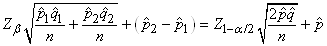 (7.360)
(7.360)
ce qui nous donne:
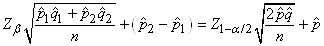 (7.361)
(7.361)
Nous avons alors après réarrangement:
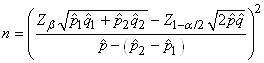 (7.362)
(7.362)
ANALYSE
DE LA VARIANCE (À UN FACTEUR)
L'objectif de l'analyse de la variance (contrairement à ce
que son nom pourrait laisser penser) est une technique
statistique
permettant
de comparer les moyennes de deux populations ou plus (très
utilisé
dans le pharma ou dans les labos de R&D ou de bancs d'essais).
Cette méthode,
néanmoins, doit son nom au fait qu'elle utilise des mesures
de variance afin de déterminer le caractère statistiquement
significatif, ou non, des différences de moyennes mesurées
sur les populations.
Plus précisément, la vraie signification est
de savoir si le fait que des moyennes d'échantillons sont
(légèrement)
différentes peut être attribué au hasard
de l'échantillonnage ou provient du fait qu'un facteur
de variabilité engendre réellement des échantillons
significativement différents (si nous avons les
valeurs de toute la population, nous n'avons rien à faire!).
Pour plus d'informations au niveau du vocabulaire et la mise
en application, l'ingénieur et le chercheur se reporteront à
la norme ISO 3534-3:1999.
Pour l'analyse de la variance appelée "ANOVA
à un facteur" (ANalysis
Of VAriance) ou "ANAVAR à un
facteur" (ANAlyse
de la VARiance), ou encore "ANOVA à une
voie" ou plus rigoureusement "ANOVA
à un facteur fixe avec répétitions" ou
encore "ANOVA à une variable catégorielle
fixe avec répétition",
nous allons d'abord rappeler, comme nous l'avons démontré,
que la loi de Fisher-Snedecor est donnée
par le rapport de deux variables aléatoires indépendantes
qui suivent une loi du Khi-deux et divisée
par leur degré de liberté tel que:
 (7.363)
(7.363)
et nous allons voir maintenant son importance.
Remarque: Lorsqu'un facteur peut avoir un très grand
nombre de niveaux nous considérons le fait d'avoir choisi
un niveau
du facteur parmi une multitude de possibles comme une sélection
aléatoire. Raison pour laquelle nous parlons alors dans ce derniers
cas de "facteur
aléatoire"
qui fait l'objet d'ANOVA particulières étudiées une fois celles
à facteurs fixes maîtrisées (par exemple les ANOVA mélengeant facteurs
fixes et facteurs aléatoires sont appelées "ANOVA
mixtes").
Considérons un échantillon aléatoire de
taille n, disons  issu
de la loi issu
de la loi  et
un échantillon aléatoire de taille m, disons et
un échantillon aléatoire de taille m, disons  issu
de la loi issu
de la loi  . .
Considérons les estimateurs du maximum de vraisemblance
de l'écart-type
de la loi Normale traditionnellement notés dans le domaine
de l'analyse de la variance par:
 et et  (7.364)
(7.364)
Les statistiques ci-dessus sont celles que nous utiliserions
pour estimer les variances si les moyennes théoriques  étaient
connues. Donc nous pouvons utiliser un résultat démontré plus
haut lors de notre étude des intervalles de confiance: étaient
connues. Donc nous pouvons utiliser un résultat démontré plus
haut lors de notre étude des intervalles de confiance:
 (7.365)
(7.365)
Comme les  sont
indépendantes des sont
indépendantes des  (hypothèse
qui implique que la covariance est nulle, la réciproque n'étant
pour rappel pas toujours vraie!), les variables: (hypothèse
qui implique que la covariance est nulle, la réciproque n'étant
pour rappel pas toujours vraie!), les variables:
 (7.366)
(7.366)
sont indépendantes l'une de l'autre.
Remarque: Il existe un type d'ANOVA
prévu pour le cas où les variables
ne sont pas indépendantes (on parle alors de "covariable").
Il s'agit de l'ANCOVA qui signifie "Analyse
de la COvariance et de la VAriance" qui utilise un
mix entre la régression linéaire (cf.
chapitre de Méthodes Numériques)
et l'ANOVA. Le but de l'ANCOVA est de supprimer statistiquement
l'effet
indirect de la covariable.
Nous pouvons donc appliquer la loi de Fisher-Snedecor avec:
 et et  (7.367)
(7.367)
ainsi que:
 et et  (7.368)
(7.368)
Nous avons donc:
 (7.369)
(7.369)
Soit:
 (7.370)
(7.370)
Ce théorème nous permet de déduire l'intervalle
de confiance du rapport de deux variances lorsque la moyenne théorique
est connue. Puisque la fonction de Fisher n'est pas symétrique,
la seule possibilité pour
faire l'inférence c'est de faire appel au calcul numérique
et nous noterons alors pour un intervalle de confiance donné le
test de la manière
suivante:
 (7.371)
(7.371)
Dans le cas où les moyennes  sont
inconnues, nous utilisons les estimateurs sans biais des variances
traditionnellement notés dans le domaine de l'analyse de
la variance par: sont
inconnues, nous utilisons les estimateurs sans biais des variances
traditionnellement notés dans le domaine de l'analyse de
la variance par:
 et et  (7.372)
(7.372)
Pour estimer les variances théoriques, nous utilisons le résultat
démontré plus haut:
 et et  (7.373)
(7.373)
Comme les  sont
indépendantes des sont
indépendantes des  (hypothèse!),
les variables: (hypothèse!),
les variables:
 (7.374)
(7.374)
sont indépendantes l'une de l'autre. Nous pouvons donc appliquer
la loi de Fisher-Snedecor avec:
 et et  (7.375)
(7.375)
ainsi que:
 et et  (7.376)
(7.376)
Nous avons donc:
 (7.377)
(7.377)
Soit:
 (7.378)
(7.378)
Ce théorème nous permet de déduire l'intervalle
de confiance du rapport de deux variances lorsque la moyenne empirique
est connue.
Puisque la fonction de Fisher n'est pas symétrique, la seule
possibilité pour
faire l'inférence c'est de faire appel au calcul numérique
et nous noterons alors pour un intervalle de confiance donné
le "test de Fisher" de la manière suivante:
 (7.379)
(7.379)
tout en se rappelant que son utilisation nécessite implicitement
des contraintes de normalité des variables étudiées.
R. A. Fisher (1890-1962) est, comme Karl Pearson, l'un des principaux
fondateurs de la théorie moderne de la statistique. Fisher étudia à Cambridge
où il obtint en 1912 un diplôme en astronomie. C'est en étudiant
la théorie de l'erreur dans les observations astronomiques que
Fisher s'intéressa à la statistique. Fisher est l'inventeur de
la branche de la statistique appelée l'analyse de la variance.
Au début du 20ème siècle, R. Fischer développe
donc la méthodologie
des plans d'expérience (cf. chapitre
de Génie Industriel).
Pour valider l'utilité d'un
facteur, il met au point un test permettant d'assurer que des échantillons
différents sont de natures différentes. Ce test est
basé sur l'analyse
de la variance (des échantillons), et nommé ANOVA
(analyse normalisée
de la variance).
Prenons k échantillons
de n valeurs aléatoires chacun. Chacune des valeurs étant considérée
comme une observation ou une mesure de quelque chose ou sur la
base de quelque chose (un lieu différent, ou un objet différent...
bref: un seul et unique facteur de variabilité entre les échantillons!).
Nous aurons donc un nombre total de N d'observations
(mesures) donné
par:
 (7.380)
(7.380)
si chacun des échantillons a un nombre identique de valeurs
n (taille de l'échantillon) tel que  nous
parlons alors de "plan équilibré" à k niveaux
(ou k modalités). nous
parlons alors de "plan équilibré" à k niveaux
(ou k modalités).
Remarque: Si nous avons plusieurs
facteurs de variabilité (par
exemple: chaque lieu compare à lui-même plusieurs
laboratoires), nous parlerons alors d'ANOVA multifactorielle. Dès
lors, s'il n'y a que deux facteurs de variabilité, nous
parlons d'ANOVA à deux facteurs (voir plus loin pour plus
de détails les différentes ANOVA à deux facteurs).
Nous considérerons que chacun des k échantillons est
issu (suit) d'une variable aléatoire suivant une loi Normale.
Facteur 1 |
Échantillon 1 |
Échantillon 2 |
Échantillon...i |
Échantillon k |

|

|
... |

|

|

|
... |

|
... |
... |

|
... |

|

|
... |

|
Moyenne:  |
Moyenne:  |
Moyenne:  |
Moyenne:  |
Figure: 7.15 - Structure typique dite "croisée" d'une analyse de la
variance à 1 facteur
En termes de test, nous voulons tester si les moyennes des k échantillons
de taille n sont égales sous l'hypothèse
que leurs variances sont égales. Ce
que nous écrivons sous forme d'hypothèse de la manière
suivante:
 (7.381)
(7.381)
Autrement dit: les échantillons sont représentatifs
d'une même
population (d'une même loi statistique). C'est-à-dire que
les variations constatées entre les valeurs des différents échantillons
sont dues essentiellement au hasard. Pour cela nous étudions
la variabilité des résultats dans les échantillons
et entre les échantillons. Il revient exactement au même
de poser que (formulation qu'on retrouve dans certains articles
ou
ouvrages):
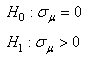 (7.382)
(7.382)
Nous noterons donc pour la suite i l'indice d'échantillon
(de 1 à k)
et j l'indice de l'observation (de 1 à n).
Donc  sera
la valeur de la j-ème observation de l'échantillon
de données
numéro i (nous avons choisi d'inverser la notation
d'usage donc attention à ne pas vous tromper par la suite...
nous sommes désolés... c'était une bêtise!). sera
la valeur de la j-ème observation de l'échantillon
de données
numéro i (nous avons choisi d'inverser la notation
d'usage donc attention à ne pas vous tromper par la suite...
nous sommes désolés... c'était une bêtise!).
Selon l'hypothèse susmentionnée, nous avons:
 (7.383)
(7.383)
Nous noterons par  la
moyenne empirique/estimée (arithmétique) de l'échantillon i (souvent
appelée "moyenne marginale"): la
moyenne empirique/estimée (arithmétique) de l'échantillon i (souvent
appelée "moyenne marginale"):
 (7.384)
(7.384)
et  la
moyenne empirique/estimée des N valeurs (soit la
moyenne des la
moyenne empirique/estimée des N valeurs (soit la
moyenne des  )
donnée donc par: )
donnée donc par:
 (7.385)
(7.385)
En utilisant les propriétés de l'espérance et de la variance
déjà démontrées plus haut nous savons que:
 et et  (7.386)
(7.386)
avec  qui
est la moyenne des moyennes vraies qui
est la moyenne des moyennes vraies  : :
 (7.387)
(7.387)
Maintenant, introduisons 3 variances:
1. La "variance
totale" comme étant
intuitivement la variance estimée sans biais en considérant
l'ensemble des N observations
comme un seul échantillon:
 (7.388)
(7.388)
où le terme au numérateur est appelé "somme
des carrés des écarts totaux".
2. La "variance entre échantillons" (c'est-à-dire
entre les moyennes des échantillons) est aussi intuitivement
l'estimateur de la variance des moyennes des échantillons:
 (7.389)
(7.389)
où le terme au numérateur est appelé "somme
des carrés des écarts entre échantillons".
Comme nous avons démontré que si toutes les variables
sont identiquement distribuées (même variance) et indépendantes
la variance des individus vaut n fois
celle de la moyenne:
 (7.390)
(7.390)
alors la "variance des observations" (variables aléatoires
dans un échantillon) est donnée par:
 (7.391)
(7.391)
Nous avons donc ci-dessus l'hypothèse de l'égalité des variances
qui est exprimée sous forme mathématique pour les développements à suivre.
3. La "variance résiduelle" est
l'effet des facteurs dits non contrôlés.
C'est par définition la moyenne des variances des échantillons
(en quelque sorte: l'erreur standard):
 (7.392)
(7.392)
où le terme au numérateur est appelé "somme
des carrés des écarts des résidus" ou
encore plus souvent "erreur
résiduelle".
Au final, ces indicateurs sont parfois résumés
sous la forme suivante:
 (7.393)
(7.393)
Remarquons que si les échantillons n'ont pas la même taille
(ce qui est rare dans la pratique), nous avons alors:
 (7.394)
(7.394)
Remarques:
R1. Le terme  est
souvent indiqué dans l'industrie par l'abréviation SST signifiant
en anglais "Sum of Squares Total" ou
plus rarement TSS pour
"Total Sum of Squares". est
souvent indiqué dans l'industrie par l'abréviation SST signifiant
en anglais "Sum of Squares Total" ou
plus rarement TSS pour
"Total Sum of Squares".
R2. Le terme  est
souvent indiqué dans l'industrie par l'abréviation SSB signifiant
en anglais "Sum of Squares Between (samples)" ou
plus rarement SSk pour
"Sum of Squares Between treatments". est
souvent indiqué dans l'industrie par l'abréviation SSB signifiant
en anglais "Sum of Squares Between (samples)" ou
plus rarement SSk pour
"Sum of Squares Between treatments".
R3. Le terme  est
souvent indiqué dans l'industrie par l'abréviation SSW signifiant
en anglais "Sum of Squares Within (samples)"
ou plus rarement SSE pour
"Sum of Squares due to Errors". est
souvent indiqué dans l'industrie par l'abréviation SSW signifiant
en anglais "Sum of Squares Within (samples)"
ou plus rarement SSE pour
"Sum of Squares due to Errors". Indiquons que nous voyons souvent dans la littérature (nous réutiliserons
un peu plus loin cette notation):
 (7.395)
(7.395)
avec donc l'estimateur sans biais de la variance des observations:
 (7.396)
(7.396)
Avant d'aller plus loin, arrêtons-nous sur la variance résiduelle.
Nous avons donc pour des échantillons qui ne sont pas
de même taille:
 (7.397)
(7.397)
Cette écriture est souvent appelée "variance
groupée" ("pooled
variance" en anglais).
Ouvrons maintenant une petite parenthèse... Prenons le
cas particulier de deux échantillons seulement:
 (7.398)
(7.398)
Soit en introduisant l'estimateur du maximum de vraisemblance
de la variance:
 (7.399)
(7.399)
Nous pouvons d'ailleurs observer que dans le cas particulier
où:
 (7.400)
(7.400)
alors:
 (7.401)
(7.401)
Donc:
 (7.402)
(7.402)
Supposons maintenant que nous souhaitions comparer avec un certain
intervalle de confiance la moyenne de deux populations ayant une
variance différente pour savoir si elles sont de natures différentes
ou non.
Nous connaissons pour le moment deux tests pour vérifier
les moyennes. Le test-Z et le test-T. Comme dans
l'industrie il est rare que nous ayons le temps de prendre des
grands échantillons,
concentrons-nous sur le deuxième que nous avions démontré plus
haut:
 (7.403)
(7.403)
Et rappelons aussi que:
 (7.404)
(7.404)
Maintenant rappelons que nous avons démontré que si nous avions
deux variables aléatoires de loi:
 (7.405)
(7.405)
alors la soustraction (différencier) des moyennes donne
(propriété de stabilité de la loi Normale):
 (7.406)
(7.406)
Donc pour la différence de deux moyennes de variables aléatoires
provenant de deux échantillons de population nous obtenons directement:
 (7.407)
(7.407)
Et maintenant l'idée est de prendre l'approximation (sous l'hypothèse
que les variances sont égales):
 (7.408)
(7.408)
Cette approximation est appelée "hypothèse homoscédastique".
Nous avons alors l'intervalle de confiance (en supposant que nous
n'avons à notre connaissance qu'un estimateur de la variance)
suivant en se rappelant que la soustraction ou la somme de deux
variables aléatoires
indépendantes implique que leurs variances s'additionnent
toujours (et donc il en va de même pour les degrés
de liberté de la
loi de Student y relative comme nous l'avons démontré plus
haut suite à la liaison directe avec la loi du khi-2):
 (7.409)
(7.409)
avec:
 (7.410)
(7.410)
Comme l'idée dans la pratique est souvent de tester l'égalité des
moyennes théoriques (et donc que leur différence est nulle) à partir
des estimateurs connus alors:
 (7.411)
(7.411)
Dans la plupart des logiciels disponibles sur le marché, le résultat
est uniquement donné à partir du fait que le  que
nous avons est compris dans le que
nous avons est compris dans le  correspondant
à l'intervalle de confiance donné rappelons-le par: correspondant
à l'intervalle de confiance donné rappelons-le par:
 (7.412)
(7.412)
dans le cas de l'hypothèse homoscédastique (égalité des
variances/homogénéité des variances).
Remarque: Cette dernière relation est appelée " independent
2-sample T-test", ou " test-T homoscédastique" ou
encore " test-T d'égalité des
espérances
de 2 observations avec variances égales" ou
encore plus simplement mais un peu abusivement " test-T à
2 échantillons",
avec taille des échantillons
différentes et variances égales. Souvent dans la
littérature,
les deux moyennes théoriques sont égales lors de
la comparaison. Il s'en suit que nous avons alors:
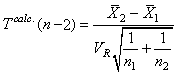 (7.413)
(7.413)
Sinon, dans le cas plus général de l'hypothèse
d'hétéroscédasticité (non égalité des
variances), nous écrivons
explicitement (nous reviendrons là-dessus lors de notre étude du
test de Welch plus loin....):
 (7.414)
(7.414)
Donc:
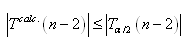 (7.415)
(7.415)
Remarque: La relation antéprécédente
est appelée " independent
two-sample T-test", ou " test-T
hétéroscédastique" ou encore
" test
d'égalité des
espérances: deux
observations avec variances différentes".
Si la taille des échantillons est
égale et que les variances le sont aussi et que nous
supposons les deux moyennes théoriques égales
lors de la comparaison, il s'ensuit que nous avons alors:
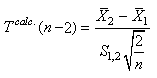 (7.416)
(7.416)
Bref, fermons cette parenthèse et revenons à nos moutons... Nous
en étions donc au tableau suivant:
 (7.417)
(7.417)
où nous avons donc dans le cas d'échantillons
de même taille:
 (7.418)
(7.418)
Ainsi que l'erreur totale qui est la somme de l'erreur
des moyennes (interclasses) et de l'erreur résiduelle
(intra-classes) et ce que les échantillons soient de même
taille ou non:
 (7.419)
(7.419)
Comme implicitiement (indirectement) il s'agit de la variance,
nous parlons alors de "décomposition
de la variance".
Effectivement:
 (7.420)
(7.420)
Or, nous avons:
 (7.421)
(7.421)
car:
 (7.422)
(7.422)
Donc:
 (7.423)
(7.423)
Maintenant, sous l'hypothèse forte (qui va
nous être
indispensable un peu plus loin) que les variances vraies sont liées
par la relation:
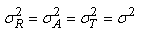 (7.424)
(7.424)
et donc que leurs estimateurs respectifs sont asymptotiquement
égaux... ce qui dans la pratique n'est approximativement
vrai que lorsque certaines conditions sont satisfaites (raison
pour
laquelle il faut absolument avant de faire une ANOVA exécuter
un calcul de la puissance et de l'effectif d'une ANOVA!) nous avons:
 (7.425)
(7.425)
ce qui découle immédiatement de la démonstration
que nous avions faite lors de notre étude de l'inférence
statistique avec la loi du Khi-deux où nous avions
obtenu (pour rappel):
 (7.426)
(7.426)
Pour déterminer le nombre de degrés de liberté de la loi du Khi-deux
de:
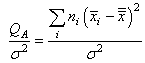 (7.427)
(7.427)
Nous allons utiliser le fait que (par le même raisonnement
que pour la relation antéprécédente):
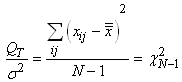 (7.428)
(7.428)
et que puisque  ,
nous devons alors avoir: ,
nous devons alors avoir:
 (7.429)
(7.429)
Il s'ensuit de par la
propriété de linéarité du Khi-deux:
 (7.430)
(7.430)
Donc pour résumer nous avons:
 et et  (7.431)
(7.431)
C'est maintenant qu'intervient la loi de Fisher dans l'hypothèse
où les variances sont égales! Puisque:
 et et  (7.432)
(7.432)
Ce que nous souhaitons faire c'est voir s'il y a une différence
entre la variance des moyennes (interclasses) et la variance résiduelle
(intra-classes). Pour comparer deux variances lorsque les moyennes
vraies sont inconnues nous avons vu que le mieux était d'utiliser
le test de Fisher. Or, nous avons démontré dans notre étude
de la loi de Fisher un peu plus haut que:
 (7.433)
(7.433)
où dans notre cas d'étude:
 (7.434)
(7.434)
Comme il existe des dizaines
de types différentes d'ANOVA il faut bien comprendre ce choix de
la plus simple des ANOVA que nous sommes entrain d'étudier maintenant.
Ainsi, si les moyennes sont les mêmes, l'hypothèse nulle est alors
que ce rapport des variances est égal à l'unité (sous les conditions
déjà susmentionnées bien plus haut). Si F vient
à être trop grand à un seuil donné, nous rejetons alors l'hypothèse
nulle d'égalité des moyennes (car in extenso les variances vont
être fortemement différentes aussi). Donc ici il semble cohérent
de comparer les variances entre groupes (numératieur) avec celle
dans les groupes (numérateur) mais comme nous le verrons ce n'est
pas toujours ce choix qui sera fait (particulièrement dans les
ANOVA hiérarchisées).
Au vu de l'hypothèse de la première égalité de
le relation ci-dessus (qui précède
l'implication), nous comprenons en même temps aussi beaucoup mieux
la très
grande sensibilité des
résultats de l'ANOVA
à la non égalité des variances vraies!
Indiquons encore que la relation précédente:
 (7.435)
(7.435)
est souvent indiquée dans la littérature sous la
forme suivante:
 (7.436)
(7.436)
où MSk est appelé "Mean
Square for treatments" et MSE "Mean
Square for Error". Ce rapport va donc nous donner la
valeur de la variable aléatoire F (dont le support
est pour rappel borné à zéro à gauche).
Concernant le choix du test (unilatéral droite/gauche ou bilatéral),
remarquons que si les moyennes sont vraiment égales, alors pour
tout i:
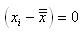 (7.437)
(7.437)
Donc dans ce cas:
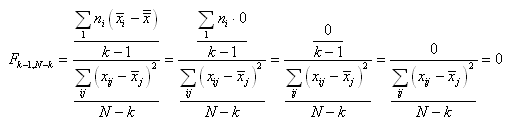 (7.438)
(7.438)
Ce qui nous amène évidemment à immédiatement adopter un test unilatéral
droite!
Sinon, en général l'interprétation de cette
fraction est donc en gros la suivante: Il s'agit du rapport (normalisé au
nombre de degrés
de liberté) de la somme de l'erreur des moyennes (interclasses)
et
de l'erreur résiduelle
(intra-classes) ou autrement dit le rapport de la variance interclasse
par la variance résiduelle. Ce rapport suit donc une loi
de Fisher à deux
paramètres donnés par les degrés de liberté des
classes respectives.
Remarque:
S'il y a seulement deux populations (échantillons), il faut
bien comprendre qu'à ce
moment l'utilisation du test-T de Student suffit amplement
et est considéré comme équivalent! Au fait,
l'ANOVA est une comparaison indirecte des moyennes, Student une
comparaison directe... il est donc évident de deviner lequel
est le mieux dans cette situation particulière!
Tous les calculs que nous avons faits sont très souvent
représentés
dans les logiciels sous la forme d'une table standardisée
dont voici la forme et le contenu (c'est ainsi que le présente
Microsoft Excel 11.8346 ou Minitab 15.1.1 par exemple):
Source |
Somme des carrés |
ddl du  |
Moyenne des carrés |
F |
Valeur critique Fc |
Inter-Classe |

|
k-1 |

|

|

|
Intra-Classe |

|
N-k=k(n-1) |

|
|
|
Total |

|
N-1=kn-1 |
|
|
|
Tableau: 7.2
- Terminologie et paramètres traditionnels d'un Tableau ANOVA (TAV) à un
facteur
ainsi, pour que l'hypothèse nulle ne soit
pas rejetée, il faut que la valeur de:
 (7.439)
(7.439)
soit plus petite ou égale au
centile de la même loi F avec une probabilité
cumulée
correspondante à 1 soustrait de niveau de confiance  . .
La valeurs choisie du F critique est
un peu malheureuse à mon avis dans les tableaux d'ANOVA
(mais bon une fois que l'on sait que c'est ainsi...). Il est
peut-être plus aisé de comprendre cette valeur
si nous l'introduisons ainsi (le test unilatéral à droite ressort
pédagogiquement mieux à mon avis):
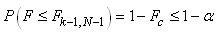 (7.440)
(7.440)
Il faut donc pour que le test ne soit pas rejeté
que:
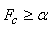 (7.441)
(7.441)
Donc la valeur critique de F correspond simplement
et bêtement à la probabilité cumulée de la p-value.
Il faut cependant bien se rappeler que pour
utiliser l'ANOVA, on doit donc supposer que les échantillons
sont issus d'une même population (données appariées)
et suivent une loi normale. Il est donc nécessaire de
vérifier la normalité des distributions et l'homoscédasticité (test
de Levene par exemple). Dans le cas contraire, il faut utiliser
des variantes non paramétriques de l'analyse de variance
(ANOVA de Kruskal-Wallis ou ANOVA de Friedman). Ces tests ne
sont pas encore
démontrés en détails à ce jour
sur le site.
Remarques:
R1. À noter que
dans la pratique, la variance inter-classe est très
souvent nommée "variance
inter-laboratoires"
et la variance intra-classe est in extenso souvent nommée "variance
intra-laboratoire".
R2. Il existe en ce début de 21ème siècle
plus de 50 test ou procédures de comparaison de variances.
L'opinion varie parmi les auteurs quant à leur pertinence
et l'efficacité
des tests d'homogénéité de variance
(THV). Certains affirment que ces derniers sont indispensables à réaliser
avant toute ANOVA, d'autres disent que ces tests sont de
toute façon
de piètre performance, l'ANOVA étant plus robuste
aux écarts
d'homoscédasticité que ce qui peut être
détecté par les THV,
particulièrement en cas de non-normalité. En
fait, toutes ces questions se rapport au problème
dit de Behrens-Fisher, qui est celui de la comparaison de
moyennes
sans supposer l'équivariance. Cependant parmis la
cinquantaine de tests existants, plusieurs études comparatives
ont permis de dégager les tests suivants: Test de Bartlett,
Levene et Brown-Forsythe.
R3. Lorsque certains niveaux d'un facteur sont réunis
en un seul pour être comparés à un niveau
de référence les statisticiens parlent alors
de création de "contrastes". Par exemple
un niveau: "groupe témoin" est comparé à un
niveau qui est la réunion de plusieurs niveaux qui
sont initialement "groupe test 1", "groupe
test 2" et "groupe test 3". Dans ce dernier
cas nous avons affaire bien évidemment à une
ANOVA désquilibrée.
ANALYSE DE LA VARIANCE (ANOVA À DEUX
FACTEURS SANS RÉPÉTITION)
Nous allons voir maintenant le concept d'interaction qui
est fondamental pour bien comprendre ce qu'il y a derrière
l'ANOVA à deux facteurs
(fixes) (ou "ANOVA à deux variables catégorielles fixes") sans et surtout avec
répétition.
Effectivement,
ce
n'est
qu'avec
l'ANOVA à deux
facteurs avec répétition par
construction mathématique - que l'on peut statistiquement (sous certaines
hypothèses) étudier
objectivement si deux ou plusieurs facteurs interagissent de manière significative
ensemble.
Il nous faut donc, avant de passer à la partie mathématique
pure, introduire quelques notions:
Définitions:
D1. Nous disons qu'il y a "absence
d'interaction" quand la moyenne des réponses
d'un facteur en fonction de ses niveaux varie de la même
amplitude et avec le même signe que la moyenne des réponses
d'un autre facteur en fonction de ses niveaux. Nous disons
alors que les courbes de réponses dans le diagramme des interactions
sont parallèles.
Remarque: Le parallélisme
des courbes de réponses est normal en situation
d'absence d'interaction, car cela signifie que quel que soit
le niveau de l'un ou l'autre des facteurs, la variation (si
elle existe) de la réponse sera toujours de
la même
amplitude. Ce qui est caractéristique de l'indépendance
(du moins localement).
D2. Nous disons que deux facteurs sont "en
interaction" quand la moyenne des réponses d'un
facteur en fonction de ses niveaux ne varie pas de la même
amplitude ou/et pas avec le même signe que la moyenne des
réponses d'un autre facteur en fonction de ses niveaux. Nous
disons alors que les courbes de réponses dans le diagramme
des interactions ne sont pas parallèles.
Remarque: L'absence d'interaction
est une hypothèse très
forte et une observation rare. Souvent, nous avons des interactions
ou de fortes interactions.
Pour comprendre le concept, nous aurons recours à de
petits exemples sans répétition qui permettront
de se faire une idée qualitative
du phénomène mais en aucun cas une approche scientifique de
l'interaction.
À chaque fois nous visualiserons les situations au
moyen de deux types de représentations: un graphique
illustrant les effets principaux d'une part et un diagramme
des interactions d'autre part.
Considérons le petit tableau suivant avec deux facteurs
à deux niveaux ("variables
explicatives") comportant
donc 4 cellules ("variables d'intérêt"):
|
|
Facteur 2
|
|
Facteur 1
|
Niveau 1
|
Niveau 2
|
|
Niveau 1
|
3
|
3
|
|
Niveau 2
|
3
|
3
|
Tableau: 7.3 - Premier exemple d'une petite ANOVA à deux facteurs sans répétition
Nous aurons comme représentations avec un logiciel
comme Minitab:

Figure: 7.16 - Graphique des effets principaux avec Minitab 15
Nous voyons bien qu'aucun facteur n'a un effet principal
sur quoi que ce soit. Ce qui est relativement intuitif étant
donné le contenu de tableau précédent.
Le diagramme des interactions (appelé souvent "profileur"
dans l'industrie) donne lui:

Figure: 7.17 - Diagramme des interactions avec Minitab 15
où nous pouvons constater que les facteurs n'interagissent
pas entre eux (ou se neutralisent c'est selon...). Nous disons
alors qu'il n'y a "(a priori)
aucun effet ni aucune interaction (localement)".
Au fait dans certaines expériences, l'absence d'interaction
est une hypothèse
très forte et donc souvent rare. Raison pour laquelle il faut faire attention
aux mots choisis lors de l'interprétation des graphiques d'interaction
(car ne
pas passer par les calculs purs est délicat pour cette étape voire
non scientifique!).
Maintenant considérons le tableau suivant:
|
|
Facteur 2
|
|
Facteur 1
|
Niveau 1
|
Niveau 2
|
|
Niveau 1
|
2
|
2
|
|
Niveau 2
|
4
|
4
|
Tableau: 7.4 - Deuxième exemple d'une petite ANOVA à deux facteurs sans
répétition
Il nous paraît clair que le Facteur 1 à travers
la prise en compte de son niveau semble avoir une influence
sur la réponse. Mais voyons les différentes représentations:

Figure: 7.18 - Graphique des effets principaux et diagramme des interactions avec Minitab
15
Détaillons plus le premier graphique comme l'a proposé un
lecteur:
Ce graphique comporte 2 parties: celle de gauche
analyse les effets du facteur 1 à travers ses 2 niveaux
; celle de droite en fait de même pour le facteur 2.
Examinons
de plus près la partie de gauche:
Nous y voyons 2 points
reliés par un segment de droite. Ici le premier point,
celui pour le niveau 1, est situé à l'ordonnée 2
alors que le deuxième point, celui pour le niveau 2, est situé à l'ordonnée
4. Rappelons-nous maintenant que chaque point représente une moyenne.
Ainsi l'ordonnée du premier point est bien située à la
moyenne de (2 + 2) / 2 = 2.
Ceci étant dit et en espérant que cela a aidé à
une meilleure compréhension, revenons à nos
moutons…
Il apparaît assez clairement dans le graphique du dessus
que seul le niveau du Facteur 1 influence la réponse,
alors que le Facteur 2 n'influence en rien la réponse.
Nous disons alors qu'il y a effet principal (localement) du
Facteur1.
Sur le diagramme des interactions, nous avons la même information,
mais sous une forme différente. Nous voyons que quel
que soit le
niveau du Facteur 2, les réponses sont horizontales et donc que celui-ci
n'influence
en rien les résultats. Nous sommes alors dans une situation où "(a
priori) l'effet principal est (localement) le Facteur 1 et en absence d'interactions
entre
les facteurs".
Voyons maintenant le tableau suivant:
|
|
Facteur 2
|
|
Facteur 1
|
Niveau 1
|
Niveau 2
|
|
Niveau 1
|
4
|
2
|
|
Niveau 2
|
4
|
2
|
Tableau: 7.5 - Troisième exemple d'une petite ANOVA à deux facteurs sans
répétition
Nous pouvons cette fois observer que le Facteur 2 a une influence
mais pas le Facteur 1. Mais voyons aussi cela avec nos 2 types
de représentations:

Figure: 7.19 - Graphique des effets principaux et diagramme des interactions avec Minitab
15
Nous observons bien sur le graphique que le Facteur 1 n'a
aucune influence. Sur le diagramme du dessous c'est moins évident
mais la
superposition des deux droites montre que le Facteur 1 n'a
pas d'influence.
Nous disons alors qu'il y a "(a
priori) effet principal (localement) du Facteur 2 et absence
d'interactions entre les
facteurs".
Considérons maintenant le tableau suivant:
|
|
Facteur 2
|
|
Facteur 1
|
Niveau 1
|
Niveau 2
|
|
Niveau 1
|
3
|
1
|
|
Niveau 2
|
5
|
3
|
Tableau: 7.6 - Quatrième exemple d'une petite ANOVA à deux facteurs sans
répétition
Nous voyons que les deux facteurs ont une influence sur la
réponse. Ce que montrent bien les deux représentations
ci-dessous:

Figure: 7.20 - Graphique des effets principaux et diagramme des interactions avec Minitab
15
Nous observons bien sur le graphique du dessus que le Facteur
1 a une influence sur la réponse et qu'il en est de
même
du Facteur 2 (et
en plus de la même amplitude quel que soit le sens!). Sur le graphique du dessous
c'est moins évident mais la même conclusion est valable. Nous disons
alors que "(a priori) les deux facteurs sont (localement)
significatifs et sans interactions".
Passons au tableau suivant:
|
|
Facteur 2
|
|
Facteur 1
|
Niveau 1
|
Niveau 2
|
|
Niveau 1
|
2
|
4
|
|
Niveau 2
|
4
|
2
|
Tableau: 7.7 - Cinquième exemple d'une petite ANOVA à deux facteurs sans
répétition
qui sous cette forme n'est pas trivial à interpréter.
Mais avec les représentations nous avons tout de suite
des informations plus pertinentes:

Figure: 7.21 - Graphique des effets principaux et diagramme des interactions avec Minitab
15
Nous observons bien sur le graphique ci-dessus qu'aucun des
facteurs n'a d'influence sur la réponse a priori (même
graphique qu'au tout début avec la même moyenne).
Le diagramme du dessous nous donne une information complémentaire
par contre (!!!): Les facteurs ont une influence croisée
et comme
cette influence croisée est de même amplitude, les effets s'annulent.
Nous disons
alors que les "deux facteurs sont (localement) en
interaction F1*F2".
Considérons maintenant le tableau suivant:
|
|
Facteur 2
|
|
Facteur 1
|
Niveau 1
|
Niveau 2
|
|
Niveau 1
|
1
|
3
|
|
Niveau 2
|
5
|
3
|
Tableau: 7.8 - Sixième exemple d'une petite ANOVA à deux facteurs sans
répétition
Ce qui nous donne les deux représentations suivantes:

Figure: 7.22 - Graphique des effets principaux et diagramme des interactions avec Minitab
15
Nous observons bien sur le graphique du dessus que le Facteur
1 semble avoir une influence et que le Facteur 2 non (en moyenne!).
Le diagramme des interactions du dessous nous donne, lui aussi,
encore une fois,
une information complémentaire (!!!): C'est que les facteurs sont en interaction.
Nous disons alors que nous avons "(a priori) deux
facteurs (localement) en interaction F1*F2 où l'influence du Facteur 1 est significative".
Tableau suivant:
|
|
Facteur 2
|
|
Facteur 1
|
Niveau 1
|
Niveau 2
|
|
Niveau 1
|
3
|
3
|
|
Niveau 2
|
5
|
1
|
Tableau: 7.9 - Septième exemple d'une petite ANOVA à deux facteurs sans
répétition
Nous voyons que les deux facteurs ont une influence sur la
réponse. Ce que montrent bien les deux représentations
ci-dessous:

Figure: 7.23 - Graphique des effets principaux et diagramme des interactions avec Minitab
15
Nous disons ici que nous avons "(a
priori) les deux facteurs (localement) en interaction F1*F2
où l'influence du Facteur 2 est
significative".
Et enfin un dernier tableau
|
|
Facteur 2
|
|
Facteur 1
|
Niveau 1
|
Niveau 2
|
|
Niveau 1
|
1
|
1
|
|
Niveau 2
|
5
|
1
|
Tableau: 7.10 - Huitième exemple d'une petite ANOVA à deux facteurs sans
répétition
qui nous donne les deux représentations:

Figure: 7.24 - Graphique des effets principaux et diagramme des interactions avec Minitab
15
Nous disons ici que nous avons "(a
priori) les deux facteurs (localement) en interaction F1*F2
où l'influence des deux facteurs
est significative".
Remarque: Une croyance (communément répandue)
de personnes qui manquent d'expérience dans les laboratoires
consiste à penser que pour qu'une interaction soit significative il est nécessaire
que les facteurs qui la composent le soient également.
Après tous ces tableaux, passons à partie mathématique:
Nous avons vu précédemment comment effectuer une analyse
de la variance à un facteur. Pour rappel, cela consiste donc à faire
un test d'égalité des espérances pour k échantillons
indépendants de n variables aléatoires chacun (dans
le cas où tous les échantillons ont donc le même nombre de
mesures). Chaque échantillon étant considéré comme une expérience
sur un sujet différent ou identique considéré alors comme un
facteur variable indépendant!
Cependant il arrive dans la réalité que pour chaque échantillon
on fasse varier un deuxième paramètre, considéré alors comme
un deuxième facteur variable. Nous parlons alors bien évidemment
d'analyse de la variance à deux facteurs. De plus, nous allons
considérer dans un premier temps pour simplifier les calculs
que les variables aléatoires sont indépendantes! Donc un facteur
n'a pas d'influence sur l'autre!!! En d'autres, termes il n'y
a pas d'interaction entre les facteurs. Nous parlons alors
d'une "ANOVA à deux facteurs sans interactions".
Afin de déterminer la formulation du test à effectuer, rappelons
que pour l'analyse de la variance à un facteur, nous avions
décomposé la
variance totale en la somme de la variance des moyennes (interclasses)
et de la variance résiduelle (intra-classes) telle que:
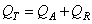 (7.442)
(7.442)
en explicitant le fait que nous comparions les échantillons 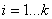 : :
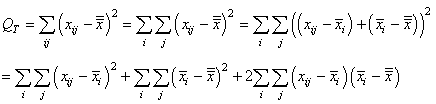 (7.443)
(7.443)
ce qui nous avait donné au final:
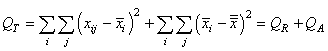 (7.444)
(7.444)
Pour l'ANOVA à deux facteurs nous partirons du tableau suivant
("Éch." est l'abréviation de "Échantillon"):
|
Facteur A |
|
Facteur B |
Éch.1 |
Éch.2 |
Éch....j |
Éch.r |
|
Éch. 1 |

|

|
... |

|
Moyenne:  |
Éch.2 |

|

|
... |

|
Moyenne:  |
Éch. i |
... |
... |

|
... |
Moyenne:  |
Éch. k |

|

|
... |

|
Moyenne:  |
|
Moyenne:  |
Moyenne:  |
Moyenne:  |
Moyenne:  |

|
Figure: 7.25 - Structure typique dite "croisée" d'une analyse de la variance à 2 facteurs
sans répétition
pour lequel dans un laboratoire, le facteur maintenu fixe
pendant qu'on fera varier l'autre sera appelé le "facteur
bloc"
et l'autre sera appelé le "facteur
de traitement" et dans la pratique on fera en sorte
que ce dernier ne soit pas effectué toujours dans le
même ordre
afin d'éliminer des éventuels effets d'inertie
lors du passage d'un traitement à l'autre (les américains
désignent les ANOVA à deux facteurs contrôlés
sans interactions sous les termes:
"randomized block design" (GRBD)).
Pour la suite, toute l'astuce consiste à décomposer la variance
totale en comparant l'espérance des lignes (observations) indexées
cette fois-ci avec 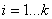 et
des colonnes (échantillons) indexées avec et
des colonnes (échantillons) indexées avec 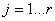 par
rapport à la moyenne totale telle que: par
rapport à la moyenne totale telle que:
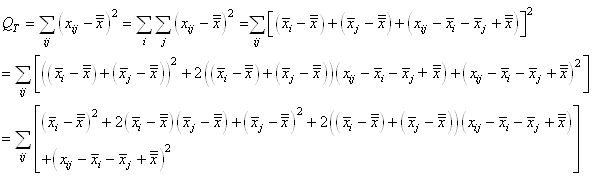 (7.445)
(7.445)
Or, nous avons dans un premier temps:
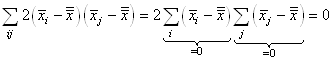 (7.446)
(7.446)
Donc il reste:
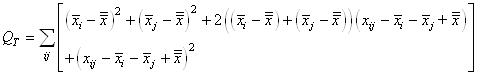 (7.447)
(7.447)
Mais nous avons aussi:
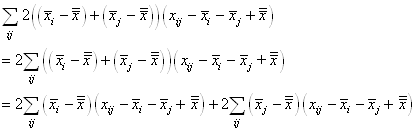 (7.448)
(7.448)
Pour la suite, indiquons d'abord que relativement à notre
tableau, nous avons:
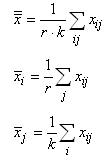 (7.449)
(7.449)
Il s'ensuit alors que:
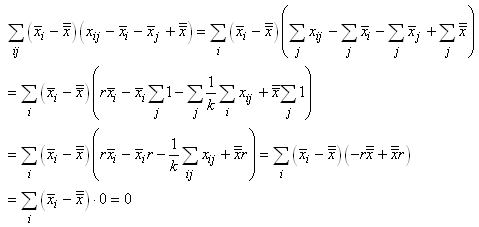 (7.450)
(7.450)
et il vient alors immédiatement que nous avons de même:
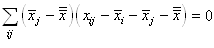 (7.451)
(7.451)
Donc il reste au final:
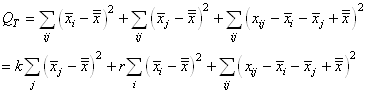 (7.452)
(7.452)
ce que nous noterons sur ce site de la manière condensée
suivante:
 (7.453)
(7.453)
où  sont
bien évidemment associés aux effets principaux (comparaison
des moyennes marginales avec la moyenne totale). sont
bien évidemment associés aux effets principaux (comparaison
des moyennes marginales avec la moyenne totale).
Donc en comparaison à l'ANOVA à un facteur nous avons un
terme supplémentaire pour la variance totale.
Dans l'ordre il est évident que la première somme des écarts
par rapport au premier facteur colonne:
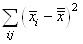 (7.454)
(7.454)
aura au même titre que l'ANOVA à un facteur 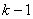 degrés
de liberté. C'est-à-dire que sous les mêmes hypothèses que
l'ANOVA à un facteur: degrés
de liberté. C'est-à-dire que sous les mêmes hypothèses que
l'ANOVA à un facteur:
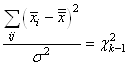 (7.455)
(7.455)
La deuxième somme des écarts par rapport au deuxième facteur
ligne:
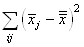 (7.456)
(7.456)
est nouvelle mais cependant on démontre de manière parfaitement
identique au premier qu'elle aura 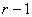 degrés
de liberté. C'est-à-dire que sous les mêmes hypothèses que
l'ANOVA à un facteur: degrés
de liberté. C'est-à-dire que sous les mêmes hypothèses que
l'ANOVA à un facteur:
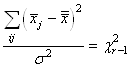 (7.457)
(7.457)
Pour la troisième somme qui suit obligatoirement aussi une
loi du Khi-deux (étant donné que la variance totale suit une
loi du Khi-deux et que les deux premiers termes de la somme
aussi!):
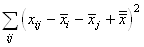 (7.458)
(7.458)
c'est un peu plus délicat... mais il y a une astuce à la
sauce physicienne...! Nous savons de par notre étude de l'ANOVA à un
facteur que la somme des degrés de liberté de chaque terme
doit être égale au nombre total de degrés de libertés. En d'autres
termes, nous devons avoir pour l'ANOVA à deux facteurs:
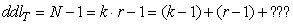 (7.459)
(7.459)
Donc il manque bien évidemment:
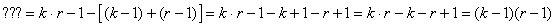 (7.460)
(7.460)
Ainsi:
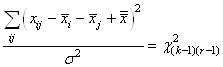 (7.461)
(7.461)
Donc nous avons alors le tableau suivant:
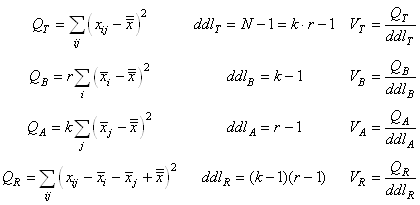 (7.462)
(7.462)
Enfin, le reste est exactement le même que pour l'ANOVA à un
facteur simplement que nous avons deux tests à effecteur cette
fois-ci qui sont:
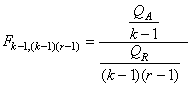 et et 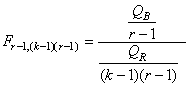 (7.463)
(7.463)
Le choix ci-dessus semble intuitivement judicieux.
Tous les calculs que nous avons faits précédemment sont très
souvent représentés dans les logiciels sous la forme d'une
table standardisée dont voici la forme et le contenu (c'est
ainsi que le présente Microsoft Excel 11.8346 ou Minitab15.1.1
par exemple):
Somme des carrés |
ddl  |
Moyenne des carrés |
F |
Valeur critique F |

|
r-1 |

|

|

|

|
k-1 |

|

|

|

|
(k-1)(r-1) |

|
|
|

|
N-1 |
|
|
|
Tableau: 7.11 - Terminologie et paramètres traditionnels d'un Tableau ANOVA (TAV) à deux
facteurs sans répétition
et la condition d'acception de l'hypothèse d'égalité des
moyennes pour chaque facteur est la même que pour l'ANOVA à un
facteur (voir le serveur d'exercice pour un exemple pratique
et détaillé avec Microsoft Excel 11.8346).
Nous avons donc deux tests de Fisher permettant chacun
de savoir si le facteur A (respectivement B)
ont une influence significative ou pas sur les mesures.
Évidemment, dans les développements ci-dessus, les facteurs A et B sont
interchangeables dans les développements par symétrie!
ANALYSE DE LA VARIANCE À DEUX FACTEURS À MESURES RÉPÉTÉES
Jusqu'à présent nous avons examiné des ANOVA sur des expériences à un
ou deux facteurs fixes (autrement dit: une ou deux variables
catégorielles). Dans le cas à deux
facteurs, nous avons considéré que
pour chaque combinaison de facteurs nous n'avions qu'une seule
mesure (cellule). Or, il peut arriver (et c'est préférable)
que nous ayons plusieurs mesures pour une combinaison!
Nous qualifions ce type d'étude de "plan
expérimental à mesures
répétées" et les résultats seront traités avec
une analyse de la variance à deux facteurs à mesures répétées
et avec interactions! Il s'agit d'un outil extrêmement important
puisqu'il permet de valider des études menées par plusieurs
laboratoires (ou employés) indépendants et il est également
associé à de nombreux
autres outils statistiques comme celui de l'étude de la reproductibilité et
de la répétabilité (Étude R&R) pour ne citer que le plus
connu dans le domaine industriel.
Il faut comprendre qu'il est obligatoire dans le domaine de
la statistique d'associer les interactions entre facteurs systématiquement
lorsque nous avons affaire à une expérience à mesures répétées.
Ceci pour la simple raison que le terme mathématique d'interaction
n'apparaît que dans cette situation.
Ainsi, il peut être intuitif (avant même de le démontrer)
qu'une ANOVA à deux facteurs (fixes) à mesures répétées (les
américains désignent les ANOVA à deux
facteurs contrôlés avec interactions sour les
termes: "generalized randomized
block design" (GRBD)) contient
une interaction double, et deux effets principaux. Une ANOVA à trois
facteurs (fixes) et à mesures répétées aura in extenso une
interaction triple, trois interactions doubles et 3 effets
principaux.
Et ainsi
de suite...
Avant de commencer, nous allons considérer le tableau de mesures
suivant où l'abréviation "Éch." fait référence au
mot "échantillon":
|
Facteur A |
|
Facteur B |
Éch. 1 |
Éch. 2 |
Éch ...j |
Éch. r |
Moyenne |
Éch.1 |

|

|
... |

|
|
Réplication
2 |

|

|
... |

|
|
Réplication m |
... |
... |
... |
... |
|
Réplication n |

|

|
... |

|
|
Moyenne Éch. 1 |

|

|
... |

|

|
Éch.2 |

|

|
... |

|
|
Réplication
2 |

|

|
... |

|
|
Réplication m |
... |
... |
... |
... |
|
Réplication n |

|

|
... |

|
|
Moyenne Éch. 2 |

|

|
... |

|

|
Éch.i |
... |
... |

|
... |
|
Réplication
2 |
... |
... |
... |
... |
|
Réplication m |
... |
... |
... |
... |
|
Réplication n |
... |
... |

|

|
|
Moyenne Éch. i |
... |
... |

|
... |

|
Éch.k |

|

|
... |

|
|
Réplication
2 |

|

|
... |

|
|
Réplication m |
... |
... |
... |
... |
|
Réplication n |

|

|
... |

|
|
Moyenne Éch. k |

|

|
... |

|

|
Moyenne |

|

|

|

|

|
Figure: 7.26 - Structure typique dite "croisée" d'une analyse de la
variance à 2 facteurs
avec répétition
avec les propriétés habituelles des moyennes (pour rappel):
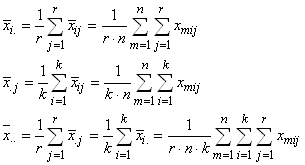 (7.464)
(7.464)
Et rappelons que pour l'ANOVA à deux facteurs sans réplications
(et donc sans interactions), toute l'astuce avait consisté à décomposer
la variance totale en comparant la moyenne des lignes indexées avec 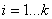 et
des colonnes indexées avec et
des colonnes indexées avec 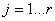 par
rapport à la moyenne totale. par
rapport à la moyenne totale.
L'idée va maintenant être à peu près la même à la différence
que nous allons comparer l'espérance des lignes indexées avec 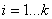 et
des colonnes indexées avec et
des colonnes indexées avec 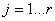 non
seulement par rapport à la moyenne totale mais aussi à celle
de chaque ligne et de chaque colonne. non
seulement par rapport à la moyenne totale mais aussi à celle
de chaque ligne et de chaque colonne.
Pour cela nous repartons de ce que nous avions obtenu pour
l'ANOVA à deux facteurs sans réplication:
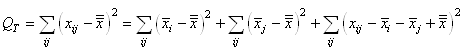 (7.465)
(7.465)
mais dont la notation sera juste adaptée au contexte:
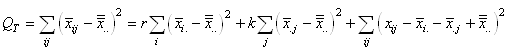 (7.466)
(7.466)
Il est évident qu'avec cette écriture l'ANOVA à deux facteurs
sans réplication deviendrait:
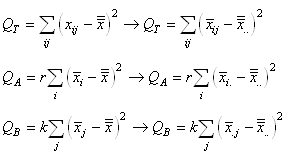 (7.467)
(7.467)
Mais dans le cas présent, il nous faut rajouter une sommation
pour les réplications et adapter la notation pour les mesures.
Donc, sans refaire tous les développements (c'est un peu culotté mais
bon...), nous obtenons déjà directement:
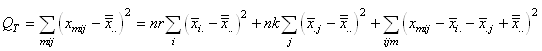 (7.468)
(7.468)
où dans l'ordre, m est la réplication de l'échantillon i du
facteur A et de l'échantillon j du facteur B.
Il vient alors bien évidemment les variances interclasses
pour les facteurs A et B qui sont immédiates:
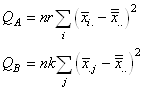 (7.469)
(7.469)
où 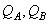 sont
bien évidemment encore une fois associées aux effets principaux
(comparaisons des moyennes marginales avec la moyenne totale). sont
bien évidemment encore une fois associées aux effets principaux
(comparaisons des moyennes marginales avec la moyenne totale).
Maintenant, nous allons jouer un peu en introduisant
sous la somme, en plus et en moins, dans le dernier terme:
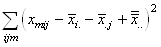 (7.470)
(7.470)
la moyenne des réplications:
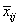 (7.471)
(7.471)
que nous retrouverons in fine dans la somme des carrés
totale:
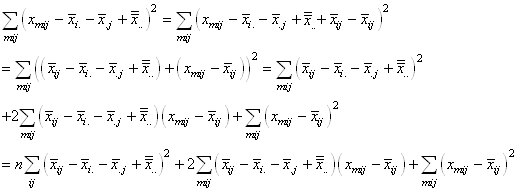 (7.472)
(7.472)
Bien entendu, nous reconnaissons assez vite la variance intra-classes
(appelée aussi souvent "erreur
résiduelle" ou simplement dans le cas particulier
de l'ANOVA à deux facteurs avec répétition "erreur
de répétabilité"):
 (7.473)
(7.473)
et le terme que nous pouvons interpréter (par comparaison
avec l'ANOVA à deux facteurs sans répétitions) comme étant
la variance d'interaction:
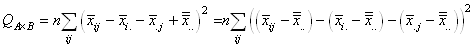 (7.474)
(7.474)
Mais si notre hypothèse est vérifiée (c'est-à-dire que l'ANOVA
est balancée), le
terme:
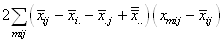 (7.475)
(7.475)
doit s'annuler. Vérifions cela:
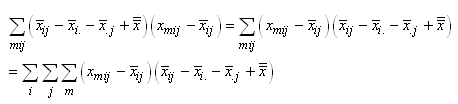 (7.476)
(7.476)
et donc pour i et j fixés il vient:
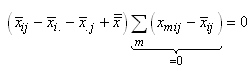 (7.477)
(7.477)
Et donc la sommation sur tous les i et j sera
aussi nulle par extension. Ceux qui ont un doute quant à l'annulation
des deux termes du développement ci-dessus, pourront peut-être
se rassurer en faisant une application numérique.
Donc au final:
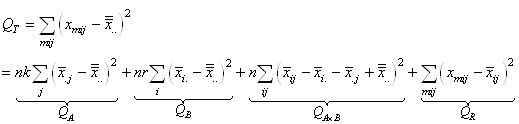 (7.478)
(7.478)
où pour rappel, n est donc le nombre de réplications, r le
nombre d'échantillons du facteur A et k le nombre
d'échantillons du facteur B (ces deux derniers paramètres
sont souvent confondus par ceux qui font les calculs à la main).
Résultat qui est parfois noté sous la forme suivante dans la
littérature:
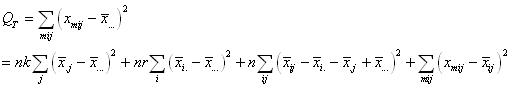 (7.479)
(7.479)
Donc en comparaison à l'ANOVA à deux facteurs sans réplications,
nous avons un terme supplémentaire pour la variance totale.
Dans l'ordre il est évident que la première somme des écarts
par rapport au premier facteur colonne:
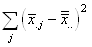 (7.480)
(7.480)
aura au même titre que l'ANOVA à un facteur et l'ANOVA à deux
facteurs sans répétition 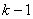 degrés
de liberté. C'est-à-dire que sous les mêmes hypothèses que
ces deux ANOVA, nous avons: degrés
de liberté. C'est-à-dire que sous les mêmes hypothèses que
ces deux ANOVA, nous avons:
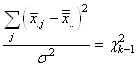 (7.481)
(7.481)
La deuxième somme des écarts par rapport au deuxième facteur
ligne:
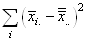 (7.482)
(7.482)
aura sous les mêmes hypothèses la propriété:
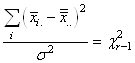 (7.483)
(7.483)
Grâce au raisonnement effectué à l'aide de l'ANOVA à deux
facteurs sans répétition, nous savons que pour le terme d'interaction:
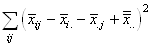 (7.484)
(7.484)
nous avons:
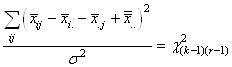 (7.485)
(7.485)
Il reste à déterminer le nombre de degrés de liberté du dernier
terme:
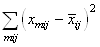 (7.486)
(7.486)
Pour ce faire, nous procédons de la même manière qu'avec
l'ANOVA à deux facteurs sans répétitions. Nous savons de par
notre étude de l'ANOVA à un facteur que la somme des degrés
de liberté de chaque terme doit être égale au nombre total
de degrés de liberté. En d'autres termes, nous devons avoir
pour l'ANOVA à deux facteurs:
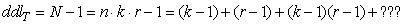 (7.487)
(7.487)
Donc il manque bien évidemment:
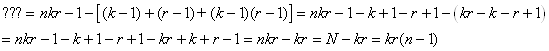 (7.488)
(7.488)
Ainsi:
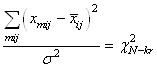 (7.489)
(7.489)
Donc nous avons alors le tableau suivant:
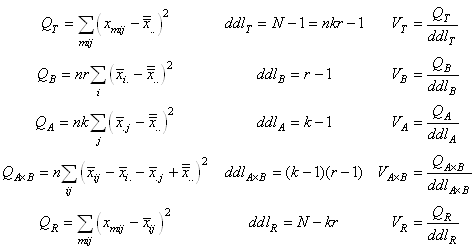 (7.490)
(7.490)
Enfin, le reste est exactement le même que pour l'ANOVA à deux
facteurs sans réplication simplement que nous avons trois tests à effecteur
cette fois-ci qui sont:
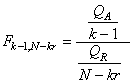 , , 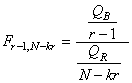 , , 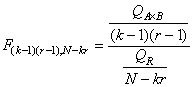 (7.491)
(7.491)
Là encore le choix des rations est relativement intuitif!
Tous les calculs que nous avons faits précédemment sont très
souvent représentés dans les logiciels sous la forme d'une
table standardisée dont voici la forme et le contenu (c'est
ainsi que le présente Microsoft Excel 11.8346 ou Minitab
15.1.1 par exemple):
Somme des carrés |
ddl  |
Moyenne des carrés |
F |
Valeur critique F |

(bloques)
|
r-1 |

|

|

|

(traitements)
|
k-1 |

|

|

|

(interactions)
|
(k-1)(r-1) |

|

|

|

|
N-kr |

|
|
|

|
N-1 |
|
|
|
Tableau: 7.12 - Terminologie et paramètres traditionnels d'un Tableau ANOVA (TAV) à deux
facteurs avec répétition
et la condition d'acception de l'hypothèse d'égalité des
moyennes pour chaque facteur est la même que pour l'ANOVA à un
facteur (voir le serveur d'exercice pour un exemple pratique
et détaillé avec Microsoft Excel 11.8346).
Nous avons donc trois tests de Fisher permettant chacun de
savoir si le facteur A (respectivement B ou
l'interaction AB) ont une influence significative ou pas sur
les mesures.
Évidemment, dans les développements ci-dessus, les facteurs A et B sont
interchangeables dans les développements par symétrie!
ANOVA MULTIFACTORIELLE À MESURES RÉPÉTÉES
L'ANOVA multifactorielle à mesures répétées
ou appelée aussi
"ANOVA multifactorielle à variables
catégorielles
et mesures répétées" (et très
rarement "ANOVA équilibrée")
est simplement le nom sous lequel les spécialistes
désignent
les ANOVA suivantes:
- ANOVA à trois facteurs (fixes) avec ou sans répétition
- ANOVA à quatre facteurs (fixes) avec ou sans répétition
- ANOVA à cinq facteurs (fixes) avec ou sans répétition - etc.
Évidemment, les ANOVA à un et deux facteurs
(fixes) font aussi partie de la famille de l'ANOVA multifactorielle
mais elles sont rarement
signalées en tant que tel dans les logiciels de statistiques
et sont souvent disponibles de façon explicite dans
les menus de ces mêmes logiciels (car ce sont les deux
plus utilisées dans les écoles). Il faut savoir
aussi que la majorité des logiciels de statistiques
gèrent
des ANOVA
multifactorielles jusqu'à 15 facteurs fixes (variables
catégorielles)
à condition que le plan soit équilibré (c'est à dire
que pour chaque niveau de chaque facteur, il y ait un nombre
identique
de mesures). Un tableur (comme Microsoft Excel) gère
le plus souvent les ANOVA jusqu'à un maximum deux facteurs
(fixes).
Bon maintenant le lecteur risque d'être déçu
(bon je suis aussi déçu de n'avoir qu'une seule
vie...) car franchement je ne souhaite pas refaire les développements
vus plus haut pour les ANOVA à un facteur et deux facteurs
(fixes) pour 3, 4 et ce jusqu'à 15 facteurs car cela
prendrait plus de 100 pages A4 sous une forme pédagogique
et claire et en plus c'est basé toujours sur la même mécanique
de développement (la théorie
généralisée
de l'ANOVA bien qu'étant beaucoup plus courte, elle
est à mon
goût
indigeste).
Remarque: Les ANOVA non équilibrées
(non balancées) nécessitent
un choix subtil de la manière de calculer les variances.
En fonction de la manière de calculer, nous parlons
d'ANOVA de type I, type II ou type III. Le choix de la méthode
de calcul est même
en ce début de 21ème siècle sujet à de
vifs débats entre spécialistes.
Raison pour laquelle nous nous abstiendrons d'étudier
ce cas-là.
TEST DE C DE COCHRAN
Le test C de Cochran a pour objet la vérification de l'homogénéité des
variances concernant plusieurs populations. Il s'agit d'un
des tests préalables ou postérieurs (post hoc) utiles
avant de faire une ANOVA balancée
(équilibrée)
et qui est recommandé par la norme ISO 5725 (de même
que le test de Tukey que nous verrons beaucoup plus loin).
Bien que l'idée du test de Cochran soit empirique, elle est
néanmoins intuitive comme le sont les définitions
des tests de Grubbs et Dixon. Pourquoi alors présentons-nous
sur ce site en détails le test C de Cochran alors que nous
avons mentionné que
nous ne le ferions pas pour le test de Grubbs et Dixon? La
raison en fait est simple: le test de Grubbs et Dixon nécessitent
des simulations par Monte-Carlo pour déterminer les valeurs
critiques de rejet ou d'acceptation de l'hypothèse nulle, alors
que la valeur critique du test C de Cochran peut être obtenue
relativement facilement analytiquement.
Ceci étant dit..., nous définissons le test C de Cochran par
le rapport:
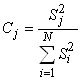 (7.492)
(7.492)
où les 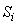 sont
les variances non biaisées des différentes sources de données
au nombre de N composées chacune de n échantillons
et l'hypothèse nulle est intuitivement l'égalité des variances
contre l'hypothèse alternative qui est qu'une des variances
est trop grande (donc mauvaise) et rejetée parce que aberrante. sont
les variances non biaisées des différentes sources de données
au nombre de N composées chacune de n échantillons
et l'hypothèse nulle est intuitivement l'égalité des variances
contre l'hypothèse alternative qui est qu'une des variances
est trop grande (donc mauvaise) et rejetée parce que aberrante.
La norme ISO 5725 recommande de réitérer ce test jusqu'à ce
qu'il n'y ait plus aucune variance aberrante (donc trop grande
ET éloignée des autres variances).
Pour déterminer la valeur critique, inversons la définition
du test C de Cochran et faisons quelques manipulations algébriques élémentaires:
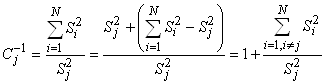 (7.493)
(7.493)
Nous remarquons qu'à peu de choses près, le deuxième terme
de la dernière égalité ressemble presqu'à une loi de Fisher.
Comme la loi de Fisher n'est pas stable par l'addition, il
faudrait que nous trouvions une manière de transformer le terme:
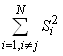 (7.494)
(7.494)
en une variance unique. L'idée est alors relativement simple
mais encore fallait-il y penser... Nous savons que les 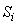 sont
des variances non biaisés avec un facteur sont
des variances non biaisés avec un facteur 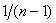 .
Donc si les N échantillons (niveaux) sont tous indépendants,
la variance globale est alors par stabilité de la loi Normale
et en reprenant les notations de l'ANOVA: .
Donc si les N échantillons (niveaux) sont tous indépendants,
la variance globale est alors par stabilité de la loi Normale
et en reprenant les notations de l'ANOVA:
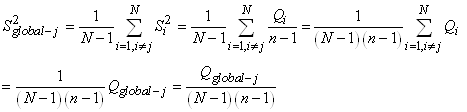 (7.495)
(7.495)
Dès lors:
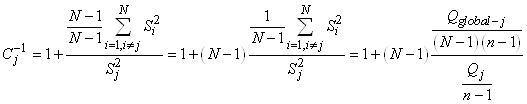 (7.496)
(7.496)
Nous reconnaissons donc dans la dernière égalité le rapport
de deux variances au carré. Nous avons alors identiquement à ce
que nous avons démontré lors de notre étude de l'ANOVA à un
facteur sans réplications:
 (7.497)
(7.497)
et donc il vient:
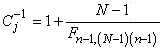 (7.498)
(7.498)
qui est dès lors indépendant de j et donc le test unilatéral
gauche (puisque par définition le rapport du test de Cochran
doit être le plus petit possible) C de Cochran aura pour valeur
critique:
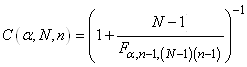 (7.499)
(7.499)
Il y a cependant un petit couac avec la relation précédente.
Effectivement, nous savons que nous devons itérer le test plusieurs
fois. Mais bien évidemment, plus nous effectuons de test sur
un échantillon
de données, plus grande est la probabilité de
rejeter l'hypothèse
nulle à un moment ou à un autre. Ce problème est appelé "inflation
du niveau de confiance" et dans la vie réelle nous
connaissons bien son application: plus on attend, plus la probabilité qu'un événement
rare ait lieu est élevée. Bien évidemment, il faut alors réduire
la valeur du seuil mais dès lors cela augmente la difficulté de
détecter les vrais effets. Dès lors, la démarche est la suivante.
Si nous considérons un test avec un niveau de signification 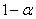 (correspondant
donc à la probabilité cumulée de ne pas faire une erreur de
type I) et que nous réitérons celui-ci de manière indépendante
une deuxième fois. Alors, si les tests sont indépendants, de
par l'axiome des probabilités, la probabilité de ne pas faire
une erreur du type I sera le produit des probabilités: (correspondant
donc à la probabilité cumulée de ne pas faire une erreur de
type I) et que nous réitérons celui-ci de manière indépendante
une deuxième fois. Alors, si les tests sont indépendants, de
par l'axiome des probabilités, la probabilité de ne pas faire
une erreur du type I sera le produit des probabilités:
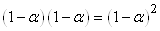 (7.500)
(7.500)
et ainsi de suite pour n tests. Nous remarquons alors
très vite que la probabilité cumulée de ne pas faire une erreur
de type I décroit très vite. Par exemple, pour 10 tests réitérés
indépendants avec un niveau de 5%, nous avons alors:
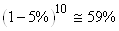 (7.501)
(7.501)
ce qui est catastrophique! Dès lors, si nous voulons un niveau
de confiance sur tests réitérés d'une certaine valeur que
nous noterons 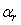 ,
il paraît évident qu'il faut résoudre l'équation suivante: ,
il paraît évident qu'il faut résoudre l'équation suivante:
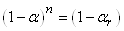 (7.502)
(7.502)
Soit (relation appelée parfois "équation de idàk"):
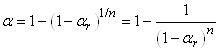 (7.503)
(7.503)
et avec un développement de Taylor au deuxième ordre il vient
(cf. chapitre Suites Et Séries):
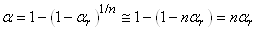 (7.504)
(7.504)
que nous appelons "approximation
de Bonferroni",
parfois "approximation de Boole" ou
encore "approximation
de Dunn". Donc au final, nous avons:
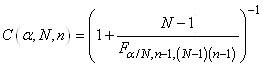 (7.505)
(7.505)
Que nous pouvons calculer avec la versin anglaise de Microsoft
Excel 14.0.6123 à l'aide
de la formule:
=1/(1+(N-1)/FINV(ALPHA/N;n-1;(N-1)*(n-1)))
(7.506)
TEST
D'AJUSTEMENT (D'ADÉQUATION) DU Khi-deux
Nous allons étudier ici notre premier test d'ajustement
non-paramétrique,
un des plus connus certainement et des plus simples (qui s'applique
seulement à des données non censurées).
Supposons qu'une variable statistique
suive une loi de probabilité P.
Si nous tirons un échantillon dans la population correspondant à cette
loi, la distribution observée, appelée "distribution
d'échantillonnage", s'écartera
toujours plus ou moins de la distribution théorique, compte
tenu des fluctuations d'échantillonnage.
Généralement, nous ne connaissons ni la forme de la loi P,
ni la valeur de ses paramètres. C'est la nature du phénomène étudié et
l'analyse de la distribution observée qui permettent de choisir
une loi susceptible de convenir et d'en estimer les paramètres. Les écarts entre la loi théorique et la distribution observée
peuvent être attribués soit aux fluctuations d'échantillonnage,
soit au fait que le phénomène ne suit pas, en réalité, la loi
supposée. En gros, si les écarts sont suffisamment faibles, nous admettrons
qu'ils sont imputables aux fluctuations aléatoires et nous accepterons
la loi retenue ; au contraire, s'ils sont trop élevés, nous en
conclurons qu'ils ne peuvent pas être expliqués par les seules
fluctuations et que le phénomène ne suit pas la loi retenue. Pour évaluer ces écarts et pouvoir prendre une décision,
il faut:
1. Définir la mesure de la distance entre distribution empirique
et distribution théorique résultant de la loi retenue.
2. Déterminer la loi de probabilité suivie
par cette variable aléatoire donnant la distance.
3. Énoncer une règle de décision
permettant de dire, d'après
la distribution observée, si la loi retenue est acceptable
ou non.
Premièrement, nous aurons pour cela besoin du théorème
central limite et deuxièmement rappelons que lors de
la construction de la loi Normale, nous avons montré que
la variable:
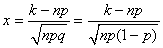 (7.507)
(7.507)
suivait une loi Normale centrée réduite lorsque n tendait
vers l'infini (condition de Laplace) et que la probabilité p
était très petite.
En pratique, l'approximation est tout à fait acceptable... dans
certaines entreprises... lorsque 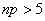 et et 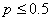 soit
(c'était un des termes qui devait tendre vers zéro quand nous
avions fait la démonstration): soit
(c'était un des termes qui devait tendre vers zéro quand nous
avions fait la démonstration):
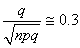 (7.508)
(7.508)
Par exemple dans les deux figures ci-dessous où nous avons
représenté les lois binomiales approchées par les lois Normales
associées, nous avons à gauche 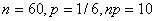 et à droite et à droite 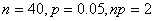 : :

Figure: 7.27 - Approche de fonctions binomiales par fonctions Normales associées
Rappelons enfin, que nous avons démontré que la
somme des carrés de n variables aléatoires
normales centrées réduites
linéairement indépendantes suit une loi du Khi-deux à n degrés
de liberté noté 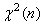 . .
Considérons maintenant une variable aléatoire X suivant
une fonction de distribution théorique (continue ou discrète) P et
tirons un échantillon de taille n dans la population correspondant à cette
loi P. Les n observations seront réparties suivant k modalités
(classes de valeurs) C1, C2, ..., Ck,
dont les probabilités p1, p2, ..., pk sont
déterminées par la fonction de distribution P (se référer à l'exemple
de la droite de Henry). Pour chaque modalité Ci, l'effectif empirique
est lui une variable aléatoire ki de loi binomiale: 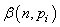 (7.509)
(7.509)
Cet effectif ki correspond en effet au nombre
de succès "résultat égal à la modalité Ci" de
probabilité pi, obtenus au cours des n tirages
d'un lot expérimental (et non dans la population de la loi théorique
comme avant). Nous avons démontré lors de l'étude de la loi binomiale que
son espérance: 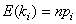 (7.510)
(7.510)
représente l'effectif théorique de la modalité Ci et
sa variance est: 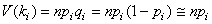 (7.511)
(7.511)
car pi est relativement petite, ce qui
donne 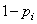 qui
est assez proche de 1. Son écart-type est donc: qui
est assez proche de 1. Son écart-type est donc:
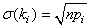 (7.512)
(7.512)
Dans ces conditions, pourvu que la modalité Ci ait un effectif
théorique npi au moins égal à 5, l'écart réduit:
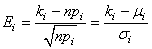 (7.513)
(7.513)
entre effectif empirique et effectif théorique peut être
approximativement considéré comme une variable normale centrée
réduite comme nous
l'avons vu plus haut.
Nous définissons alors la variable:
 (7.514)
(7.514)
où 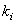 est
souvent nommée "fréquence expérimentale" et est
souvent nommée "fréquence expérimentale" et 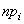 "fréquence
théorique". "fréquence
théorique".
Si nous prenons le carré c'est parce si nous ne faisions
qu'une somme simple certains termes s'annuleraient par effets
opposés
et masqueraient donc les différences, si nous prenions
la somme des valeurs absolue la table statistique de D serait
difficile à construire et le test peu robuste à cause
du faible
écart des distances. Le carré permet donc non
seulement d'avoir une table statistique pour D qui
est simple puisque basées sur une loi à un seul
paramètre comme nous allons le
voir et que cela augmente de façon suffisante la robustesse
du test (de par le carré de la différence).
Signalons que cette variable est aussi parfois (un peu malheureusement)
notée: 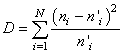 (7.515)
(7.515)
ou le plus souvent:
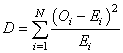 (7.516)
(7.516)
Cette variable D, somme des carrés des variables Ei,
nous donne une mesure de ce que nous pourrions appeler une "distance" ou "différence" ou "écart" entre
distribution empirique et distribution théorique. Notons
bien cependant qu'il ne s'agit pas d'une distance au sens
mathématique habituel (topologique).
Rappelons que D peut donc aussi s'écrire: 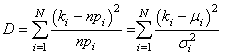 (7.517)
(7.517)
D est donc la somme des carrés de N variables
aléatoires normales centrées réduites liées par la seule
relation linéaire:
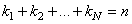 (7.518)
(7.518)
où n est la taille de l'échantillon. Donc D suit
une loi Khi-deux mais à N-1 degrés de liberté, donc un
degré de moins à cause
de l'unique relation linéaire qui les lie! Effectivement, rappelons
que le degré de liberté indique le nombre de variables indépendantes
dans la somme et non pas juste le nombre de termes sommés.
Donc:
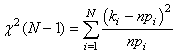 (7.519)
(7.519)
Nous appelons ce test un "test
non-paramétrique du Khi-deux" ou "test
du Khi-deux de Pearson" ou encore "test
d'ajustement
du Khi-deux" ou encore "test
de Karl Pearson" ou encore "test
d'adéquation de l'ajustement du Khi-deux"...
Ensuite, l'habitude est de déterminer la valeur de
la loi du Khi-deux à N-1 degrés de liberté ayant
5% de probabilité d'être
dépassée. Ainsi, dans l'hypothèse où le
phénomène étudié suit
la loi théorique P, il y a donc 95% de probabilité cumulée
que la variable D prenne une valeur inférieure à celle
donnée par la loi du Khi-deux.
Si la valeur de la loi du Khi-deux obtenue à partir de l'échantillon
prélevé est inférieure à celle correspondant
aux 95% de probabilité cumulée,
nous acceptons l'hypothèse selon laquelle le phénomène
suit la loi P.
Remarques:
R1. Le fait que l'hypothèse de la loi P soit
acceptée
ne signifie pas pour autant que cette hypothèse soit vraie,
mais simplement que les informations données par l'échantillon
ne permettent pas de la rejeter. De même, le fait que l'hypothèse
de la loi P soit rejetée ne signifie pas nécessairement
que cette hypothèse soit fausse mais que les informations
données
par l'échantillon conduisent plutôt à conclure à l'inadéquation
d'une telle loi.
R2. Pour que la variable D suive une loi du Khi-deux,
il est nécessaire que les effectifs théoriques npi des
différentes modalités Ci soient
au moins égaux à 5,
que l'échantillon soit tiré au hasard (pas d'autocorrélation)
et qu'aucune des probabilités pi ne
soit trop proche de zéro.
Ce test d'ajustement souffre cependant d'un gros défaut:
il nécessite
de regrouper les mesures dans des classes Ci et
dans la pratique il n'existe pas de théorème absolu
(du moins à
ma connaissance) pour choisir le nombre de classes (et in extenso
leur largeur). C'est cette raison qui fait que le test d'ajustement
(conformité) du Khi-deux est resérvé pour des distributions discrètes
où le problème du choix des classes en se pose pas.
Il nous faudra cependant créer des tests d'ajustement qui
ne nécessitent pas l'utilisation de classes et nous allons
voir de suite les outils ad hoc pour cela (test de Kolmogorov-Smirnov
ou Anderson-Darling pour ne citer qu'eux).  Exemple: Exemple:
Supposons que les naissances à un hôpital, pour une certaine période
de temps, se répartissent comme suit:
Jour |
L |
M |
M |
J |
V |
S |
D |
Total |
Observations |
120 |
130 |
125 |
128 |
80 |
70 |
75 |
728 |
Tableau: 7.13 - Mesures pour l'exemple du test du Khi-deux
Nous remarquons qu'il y a eu au total 728 naissances. Nous nous
posons alors la question suivant: Combien devrait il y avoir
de naissances, en théorie, à chaque jour s'il n'y a pas de différence
entre les jours? Ceci représente l'hypothèse nulle. En fait l'hypothèse
nulle indique que les différences entre les fréquences observées
et les fréquences théoriques sont relativement petites. Nous prenons
donc pour acquis que si aucune différence n'existe il devrait y
avoir le même nombre de naissances à chaque jour. Puisqu'il y a
au total 728 naissances pour les 7 jours en théorie il devrait
y avoir 728/7=104 naissances à chaque jour. Nous avons donc maintenant
le tableau suivant:
Jour |
L |
M |
M |
J |
V |
S |
D |
Total |
Observations |
120 |
130 |
125 |
128 |
80 |
70 |
75 |
728 |
Théorique |
104 |
104 |
104 |
104 |
104 |
104 |
104 |
728 |
Tableau: 7.14 - Comparaison par rapport à l'attendu
Le total des fréquences observées est égal au total des fréquences
théoriques. Il s'agit donc d'examiner la différence entre les fréquences
observées et les fréquences théoriques (supposées suivre une loi
uniforme) en suivant la relation du Khi-deux. En d'autres termes,
nous allons faire un test d'ajustement entre une fonction de distribution
empirique (observée) et la fonction de distribution uniforme. Nous
avons alors:

Le  est
donc de 43.49. Comme tel ce chiffre signifie peu de chose. Il faut
interpréter ce résultat grâce à l'aide de la table des valeurs
critiques du est
donc de 43.49. Comme tel ce chiffre signifie peu de chose. Il faut
interpréter ce résultat grâce à l'aide de la table des valeurs
critiques du  .
On comprend qu'il est très peu probable que la fréquence observée
et la fréquence théorique soit identique. Nous acceptons qu'il
puisse y avoir une certaine différence (nous rejetons donc l'hypothèse). .
On comprend qu'il est très peu probable que la fréquence observée
et la fréquence théorique soit identique. Nous acceptons qu'il
puisse y avoir une certaine différence (nous rejetons donc l'hypothèse).
Il ne faut donc pas oublier que ce test s'applique uniquement
à des données non censurées, c'est-à-dire pour lequel les intervalles
sont tous bornés et fermés.
TEST D'AJUSTEMENT DE
KOLMOGOROV-SMIRNOV
En statistiques, le test de Kolmogorov-Smirnov est un test d'hypothèse
d'ajusteent basé sur une distance empirique utilisé pour déterminer
si une distribution d'échantillonnage suit
bien une loi donnée connue par sa fonction de répartition
continue (ou pour comparer deux échantillons et vérifier
s'ils sont dépendants ou non car semblables ou dissemblables).
Ce test, au même titre que celui d'ajustement du khi-2, n'est
valable que pour des données non censurées (du moins
pas sans correction obtenue par simulations numériques).
Pour introduire ce test, nous avons choisi l'approche de Lilliefors
qui permet d'éviter des calculs complexes. Par ailleurs,
les logiciels qui proposent le "test
de Lilliefors" ne proposent
pas le test Kolmogorov-Smirnov
puisque ce dernier n'est correct qu'asymtotiquement (ce qui est
le cas de Tangra 4.14).
Imaginez donc que nous souhaiterions construire
un test non paramétrique
d'ajustement qui marche aussi bien pour les lois discrètes que
continues et sans souffrir du même problème
que le test d'ajustement du Khi-deux (regroupement en classes).
Pour construire ce test, nous allons partir de la fonction de
répartition empirique déjà définie au début de ce chapitre et donnée
pour rappel par
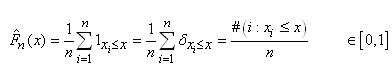 (7.520)
(7.520)
Notons maintenant  ,
la loi vraie supposée dont l'expression analytique est connue avec
laquelle nous souhaiterions comparer ,
la loi vraie supposée dont l'expression analytique est connue avec
laquelle nous souhaiterions comparer  et
construisons la distance: et
construisons la distance:
 (7.521)
(7.521)
Remarque: La loi de référence
peut provenir cependant aussi d'un autre échantillon de
mesures. L'idée est alors simplement
de compararer
deux distributions empiriques. Nous parlons alors de "test
pour 2 échantillons indépendants de Kolmogorov-Smirnov".
Certains logiciels gèrent aussi de façon empirique le cas où les
2 échantillons n'ont pas la même taille.
Le problème avec ce choix de distance c'est... quel x faut-il
alors choisir pour faire un test? Eh bien pour répondre il est
simple de constater qu'il serait stupide de prendre le x pour
lequel cette distance est minimale, car avoir un  qui
peut valoir-zéro n'apporte pas grand chose... Dès lors, on se reporte
plutôt vers le plus grand écart en valeur absolue. Ce qui nous
amène à redéfinir la distance qui
peut valoir-zéro n'apporte pas grand chose... Dès lors, on se reporte
plutôt vers le plus grand écart en valeur absolue. Ce qui nous
amène à redéfinir la distance  ainsi: ainsi:
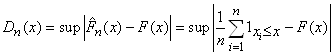 (7.522)
(7.522)
où  est
appelée "distribution empirique de Kolmogorov-Smirnov" (bon
évidemment il faudrait prouver rigoureusement qu'il s'agit
bien d'une distribution... mais pour l'instant c'est trop complexe
au niveau du contenu du présent site, cependant cela peut
se vérifier
en faisant des simulations numériques). Avant d'aller plus
loin relativement à la
théorie,
regardons un exemple pratique. est
appelée "distribution empirique de Kolmogorov-Smirnov" (bon
évidemment il faudrait prouver rigoureusement qu'il s'agit
bien d'une distribution... mais pour l'instant c'est trop complexe
au niveau du contenu du présent site, cependant cela peut
se vérifier
en faisant des simulations numériques). Avant d'aller plus
loin relativement à la
théorie,
regardons un exemple pratique.
Supposons que nous ayons mesuré les cinq valeurs suivantes:
-1.2, 0.2, -0.6, 0.8, -1.0
(7.523)
soient ordonnées:
 (7.524)
(7.524)
Nous voulons tester l'hypothèse nulle suivante:
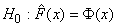 (7.525)
(7.525)
où  représente
la fonction de répartition de la loi Normale centrée réduite. représente
la fonction de répartition de la loi Normale centrée réduite.
La fonction de distribution empirique sera donnée par:
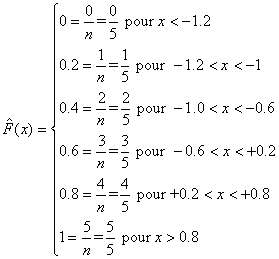 (7.526)
(7.526)
Ensuite, nous construisons traditionnellement le tableau suivant:
|
x |
 |
 |
 |
|
 |
0 |
0.115 |
0.115 |
|
 |
0.2 |
0.115 |
0.085 |
|
 |
0.2 |
0.159 |
0.041 |
|
 |
0.4 |
0.159 |
0.241 |
|
 |
0.4 |
0.274 |
0.126 |
|
 |
0.6 |
0.274 |
0.326 |
|
 |
0.6 |
0.580 |
0.020 |
|
 |
0.8 |
0.580 |
0.220 |
|
 |
0.8 |
0.788 |
0.012 |
|
 |
1 |
0.788 |
0.212 |
Souvent associé au graphique comparant les fonctions de répartition
empirique et théorique:

Figure: 7.28 - Représentation de l'approche du test d'ajustement de Kolmogorov-Smirnov
Nous voyons alors que l'écart maximal observé est 0 326. Nous
la noterons pour la suite:
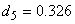 (7.527)
(7.527)
que certains logiciels comme Minitab notent par l'abréviation KS.
Le lecteur aura remarqué que le plus grand écart au-dessus de
la courbe est mesuré par:
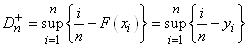 (7.528)
(7.528)
Le plus grand écart au-dessous de la courbe est mesuré par:
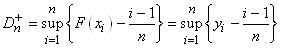 (7.529)
(7.529)
Le plus grand écart est alors:
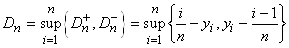 (7.530)
(7.530)
Mais que faire de cette valeur? À quoi la comparer? Eh bien l'idée
est relativement simple et consiste à générer n valeurs
(donc cinq dans le cas présent) issues de la loi de distribution
F(x) de
l'hypothèse nulle et de les comparer à elles-mêmes. Autrement dit,
il s'agit de faire une simulation de Monte-Carlo (cf.
chapitre de Méthodes Numériques)
Ainsi, dans le cas présent, nous générons 5 valeurs de N(0,1),
ce qui nous donne par exemple avec la version anglaise de Microsoft
Excel 11.8346 (je préfère
parfois donner en anglais sinon le nom des fonctions est trop long):
=NORM.S.INV(RANDBETWEEN(0;1000000)/1000000)
Nous obtenons ainsi 5 valeurs de Z (notation habituelle
de la variable aléatoire d'une loi Normale centrée réduite) qui
ordonnées seront par exemple:
-1.427, 0.082, 0.162, 0.294, 1.292
et nous refaisons le même tableau qu'avant:
|
 |
 |
 |
 |
|
 |
0 |
0.077 |
0.077 |
|
 |
0.2 |
0.077 |
0.123 |
|
 |
0.2 |
0.533 |
0.333 |
|
 |
0.4 |
0.533 |
0.133 |
|
 |
0.4 |
0.564 |
0.164 |
|
 |
0.6 |
0.564 |
0.036 |
|
 |
0.6 |
0.616 |
0.016 |
|
 |
0.8 |
0.616 |
0.184 |
|
 |
0.8 |
0.902 |
0.102 |
|
 |
1 |
0.902 |
0.098 |
Tableau: 7.15 - Tableau du test de Kolmogorov-Smirnov
Et nous avons donc l'écart maximal observé qui est de 0.333. Soit
avec la version française de Microsoft Excel 14.0.6123:

Figure: 7.29 - Calcul dans Microsoft Excel 14.0.6123
avec les formules explicites (malheureusement trop longues dans
la version française du logiciel):

Figure: 7.30 - Fonctions explicites dans Microsoft Excel 14.0.6123
avec la petite routine VBA correspondante vite fait mal faite
qui va prendre le nombre d'itérations voulues dans la cellule K1
et va mettre la distribution empirique de Kolmogorov-Smirnov dans
la colonne G de la feuille active:

Figure: 7.31 - Code VBA Microsoft Excel 14.0.6123 pour la simulation de Monte-Carlo
Nous réitérons donc la procédure un bon millier de fois et nous
obtenons la fonction de répartition (obtenue simplement en faisant
un graphique de type nuage de points dans Microsoft Excel 14.0.6123 de 2'000
simulations):

Figure: 7.32 - Fonction de réparition de Kolmogorov-Smirnov
et en appliquant un test unilatéral avec un risque 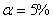 nous
obtenons pour le 95ème centile: nous
obtenons pour le 95ème centile:
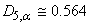 (7.531)
(7.531)
Le lecteur retrouvera la même valeur dans les tables de Kolmogorov-Smirnov
disponibles dans de nombreux ouvrages. Quelques
milliers de simulations suffisent donc pour retrouver les valeurs
des tables!
Et maintenant, nous comparons:
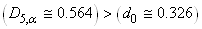 (7.532)
(7.532)
et donc nous ne rejetons pas l'hypothèse nulle.
Cependant, ... il faut tout de même se méfier avec seulement cinq
valeurs, il est tout à fait probable que l'hypothèse nulle ne soit
pas rejetée pour d'autres lois de répartition que la loi Normale.
Ainsi, comme le lecteur l'aura remarqué, pour chaque hypothèse
nulle associée à une loi donnée, il faut tabuler la distribution
empirique de Kolmogorov-Smirnov pour différentes valeurs de n et
de 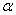 en
utilisant des méthodes numériques. Dans la majorité des ouvrages
on ne trouve qu'une seule table à l'aide d'un théorème puissant
qui montre qu'en réalité, les valeurs critiques seront les mêmes. en
utilisant des méthodes numériques. Dans la majorité des ouvrages
on ne trouve qu'une seule table à l'aide d'un théorème puissant
qui montre qu'en réalité, les valeurs critiques seront les mêmes.
Remarque: Kolmogorov et Smirnov ont démontré que lorsque n tend
est très grand et que la loi de l'hypothèse nulle est continue,
il n'est plus nécessaire de tabuler une table de Kolmogorov-Smirnov
pour chaque loi, car nous avons alors:
 (7.533)
(7.533)
donc la distribution  est
indépendante de la loi de l'hypothèse nulle. En simulant avec la
méthode de Monte-Carlo, nous observons effective une convergence
lorsque n dépasse la centaine. Mais dans la pratique, la
grande majorité du temps, il est impensable d'avoir un tel nombre
de mesures. D'où le fait que ce résultat théorique soit peu utilisé dans
la pratique et justifie l'absence de démonstration. est
indépendante de la loi de l'hypothèse nulle. En simulant avec la
méthode de Monte-Carlo, nous observons effective une convergence
lorsque n dépasse la centaine. Mais dans la pratique, la
grande majorité du temps, il est impensable d'avoir un tel nombre
de mesures. D'où le fait que ce résultat théorique soit peu utilisé dans
la pratique et justifie l'absence de démonstration.
Pour clore, signalons au lecteur qu'il trouvera la démonstration
mathématique du test d'ajustement d'Anderson-Darling un
peu plus bas.
TEST DE NORMALITÉ DE RYAN-JOINER
Considérons une variable aléatoire X dont nous connaissons la distribution d'échantillonnag et
pour laquellenous
souhaiterions vérifier la normalité ou pas. Et considérons
une variable aléatoire
ordonnée Y générée par une loi Normale centrée réduite.
Pour comparer X et Y, nous allons centrer X et
ordonner ses valeurs dans l'ordre croissant.
Pour une même taille d'échantillon, si les valeurs ordonnées de X et Y pris
deux à deux suivent une même loi, la régression linéaire de l'un
en fonction de l'autre doit donner un coefficient assez proche
de 1. En prenant la définition du coefficient de corrélation au
carré, il vient alors:
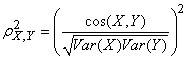 (7.534)
(7.534)
Y est imposé comme suivant une loi normale centrée réduite.
Il vient alors:
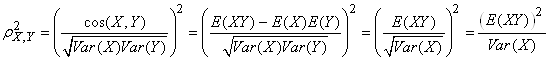 (7.535)
(7.535)
et si nous prenons l'estimateur du coefficient de corrélation:
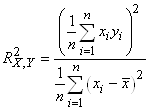 (7.536)
(7.536)
Mais comme nous avons centré X, il vient:
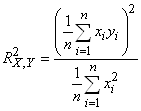 (7.537)
(7.537)
Soit après simplification:
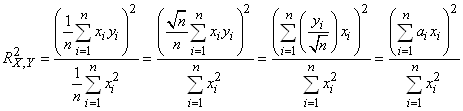 (7.538)
(7.538)
Il s'agit de l'approche de Ryan-Joiner (implémentée dans Minitab)
du test de Shapiro-Wilk. Les résultats des deux tests sont très
similaires. Les coefficients  peuvent être
facilement obtenus à l'aide de n'importe quel tableur à notre époque
en utilisant une simulation de Monte-Carlo (cf.
chapitre de Méthodes
Numériques). Si un lecteur le souhaite nous détaillerons comment
obtenir les peuvent être
facilement obtenus à l'aide de n'importe quel tableur à notre époque
en utilisant une simulation de Monte-Carlo (cf.
chapitre de Méthodes
Numériques). Si un lecteur le souhaite nous détaillerons comment
obtenir les  avec
Microsoft Excel pour un n donné. avec
Microsoft Excel pour un n donné.
Il convient de signaler que les logiciels de statistique donne
la racine carrée de la dernière égalité ci-dessous comme étant
le coefficient RJ de Ryan-Joiner.  Exemple: Exemple:
Considérons les 10 mesures de la colonne A déjà triées
dans l'ordre croissant:

Figure: 7.33 - Mesures ordonnées, rangs, coefficient de RJ et Z-score d'exemple
Les formules sont les suivantes (données en anglais car plus petites
pour la capture d'écran):

Figure: 7.34 - Détails de la capture d'écran précédent avec
la version anglophone de
Microsoft Excel 14.0.6123
Et donc nous avons dans une feuille nommée Coeff_MonteCarlo des
simulations de Monte-Carlo pour déterminer les 10 coefficients  notés
traditionnellement dans le cas de 10 mesures dans les tables sous
la forme suivante: notés
traditionnellement dans le cas de 10 mesures dans les tables sous
la forme suivante: 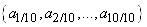 . .
D'abord il faut créer 10 colonnes avec des générations de variables
aléatoires normales centrées réduites sur à peu près 10'000 lignes
avec la formule suivante (donnée en anglais):
=NORM.S.INV(RANDBETWEEN(1;99999999)/100000000)

Figure: 7.35 - Génération des variables aléatoires normales centrées réduites pour les
coefficient de RJ
et ensuite il faut construire les ranges de toutes ces valeurs
ligne par ligne tel que:

Figure: 7.36 - Tri des simulations pour déterminer les coefficients de RJ
avec les formules suivantes (données seulement pour les 4 premiers i faute
de place dans la capture d'écran):

Figure: 7.37 - Détails du tri pour la détermination des coefficients
de
RJ
avec
la version anglophone de Microsoft Excel 14.0.6123
Pour finir, il n'y a plus qu'à calculer le coefficient de corrélation
entre les colonnes C et D de la première capture
d'écran:

Figure: 7.38 - Calcul final du coefficient de corrélation de RJ
Ce qui donne environ 0.963 (le carré de cette valeur étant très
très proche du test de Shapiro-Wilk). Ensuite, pour savoir si on
peut accepter ou rejeter l'hypothèse de normalité, il faudrait
refaire la procédure avec en lieu et place mesures, des valeurs
générées aussi aléatoires à partir d'une loi Normale et déterminer
la valeur critique d'acceptation/rejet (normalement c'est très
simple à faire mais on peut détailler sur demande).
TEST D'AJUSTEMENT d'anderson-darling
Il est surprenant qu'un test raisonnablement puissant (robuste)
comme l'est le test de Kolmogorov-Smirnov puisse être conçu
en ne s'appuyant que sur une unique observation et ce un seul point
de la fonction de répartition candidate. Il semblerait,
avec du recul, plus efficient de mesurer la différence entre
les deux fonctions de répartition en comparant ces fonctions
sur l'intégralité de leur domaine, c'est-à-dire
de 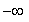 à à  . .
Il existe une famille de tests dont les statistiques sont basées
sur l'intégrale du carré de la différence
(ces tests sont souvent considérés comme non paramétriques
mais selon moi à tort et ce au même titre que le test
de Kolmogorov-Smirnov est lui aussi considéré comme
non paramétrique):
 (7.539)
(7.539)
entre la fonction de répartition empirique et la fonction
de répartition de référence. La plus simple
de ces statistiques est:
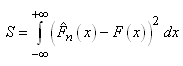 (7.540)
(7.540)
qui est simplement la surface comprise entre la fonction
de répartition empirique et la fonction de répartition
de référence. Soit, en reprenant le graphique utilisé
plus haut lors de notre étude du test d'ajustement de Kolmogorov-Smirnov:

Figure: 7.39 - Représentation de l'approche du test d'ajustement d'Anderson-Darling
Cependant, arbitrairement, nous pouvons choisir autre chose que
la mesure x pour l'intégrale. Ainsi, un choix classique
est de prendre la fonction de répartition théorique
elle-même comme mesure de base de l'intégrale. Il
vient ainsi:
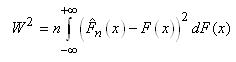 (7.541)
(7.541)
La statistique résultant de cet ajout s'appelle
la "statistique de Cramér-von Mises". Cependant
elle souffre d'un gros défaut de robustesse lorsque des
points de mesures se trouvent sur les queues de la distribution.
Il a alors été proposé la mesure
suivante qui est un peu moins sensible aux points de mesures se
trouvant sur les queues:
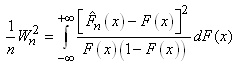 (7.542)
(7.542)
appelée "statistique
d'Anderson-Darling" qui
a été la plus utilisée dans la fin du 20ème siècle
et reste dominante au début du 21ème aussi (du moins tant que
l'échantillon est d'une taille acceptable!). Elle est par construction plus
robuste que les statistiques de Cramér-von
Mises et de Kolmogorov-Smirnov mais des études par simulations ont montré qu'elle était
moins robuste que le test de Shapiro-Wilk ou Ryan-Joiner.
En se rappelant que la définition de la distribution
empirique 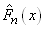 lors
de notre étude
du test d'ajustement (adéquation) de Kolmogorov-Smirnov implique que: lors
de notre étude
du test d'ajustement (adéquation) de Kolmogorov-Smirnov implique que:
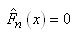 (7.543)
(7.543)
si 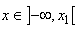 et: et:
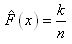 (7.544)
(7.544)
si 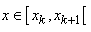 et: et:
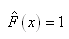 (7.545)
(7.545)
si  .
Nous avons alors en supposant en plus que F est continue: .
Nous avons alors en supposant en plus que F est continue:
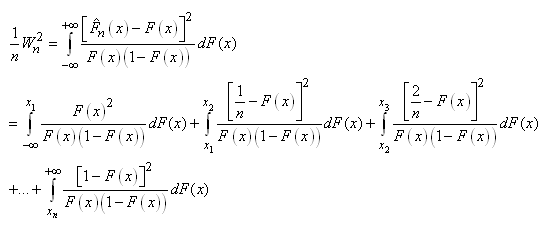 (7.546)
(7.546)
Ensuite, nous faisons le changement de variable:
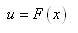 (7.547)
(7.547)
et donc:
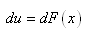 (7.548)
(7.548)
et sans oublier les changement de bornes des intégrales
puisque:
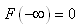 et et
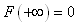 (7.549)
(7.549)
Il vient alors:
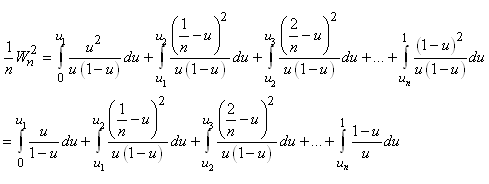 (7.550)
(7.550)
où nous avons bien évidemment posé:
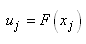 (7.551)
(7.551)
Il faut à présent calculer ces intégrales.
Nous cherchons donc la primitive d'une fonction du type:
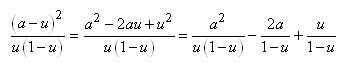 (7.552)
(7.552)
Les primitives des deux expressions suivantes:
 (7.553)
(7.553)
ont été démontrées sous leur forme
générale dans le chapitre de Calcul Différentiel Et Intégral
et valent respectivement:
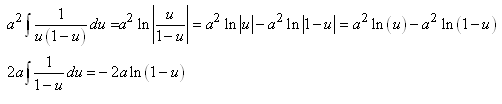 (7.554)
(7.554)
car au vu des valeurs que peut prendre u, il est alors inutile
d'indiquer les valeurs absolues.
Il nous reste donc qu'à calculer la primitive de:
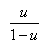 (7.555)
(7.555)
où un changement de variable évident (si jamais
vous souhaitez les détails n'hésitez pas à demander) nous
donne la primitive sans la constante:
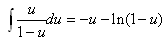 (7.556)
(7.556)
Nous avons alors au final:
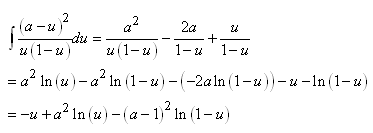 (7.557)
(7.557)
Nous avons donc:
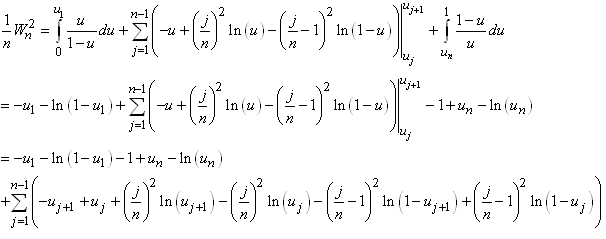 (7.558)
(7.558)
Nous pouvons déjà remarquer que dans la dernière égalité:
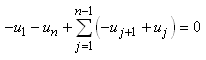 (7.559)
(7.559)
Il reste alors:
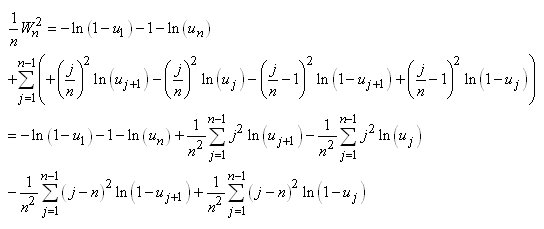 (7.560)
(7.560)
Nous allons procéder maintenant à quelques manipulations
algébrique astucieuses (mais simples) pour condenser l'écriture
de cette dernière égalité.
D'abord, remarquons que nous pouvons récrire la première somme
ainsi (le lecteur pourra vérifier en développement les deux sommes
pour une petite valeur de n):
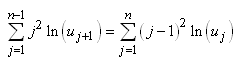 (7.561)
(7.561)
ce qui équivaut donc à poser 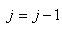 . .
Nous transformons aussi la deuxième somme:
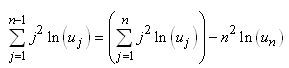 (7.562)
(7.562)
et le lecteur pourra vérifier que l'égalité ci-dessous
pour la troisième somme est vérifiée:
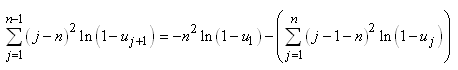 (7.563)
(7.563)
qui équivaut aussi à poser 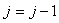 . .
Enfin, nous transformons la quatrième somme (puisque de
toute façon lorsque j vaut n le terme de la somme est nul...):
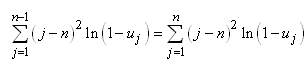 (7.564)
(7.564)
Alors, nous avons:
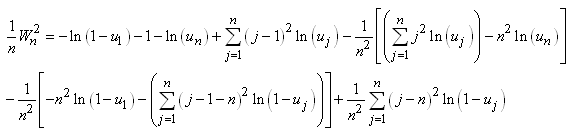 (7.565)
(7.565)
Soit en éliminant les termes qui s'annulent:
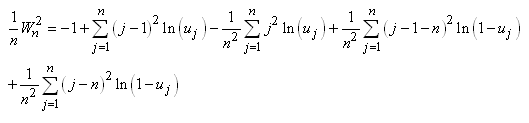 (7.566)
(7.566)
Et en regroupant les termes ayant la même forme de logarithme:
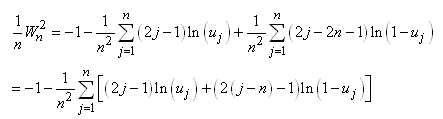 (7.567)
(7.567)
Soit:
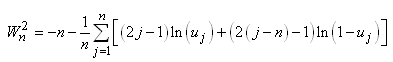 (7.568)
(7.568)
Il s'agit d'un des formes du test d'Anderson-Darling et qui dans
le cadre d'une loi Normale s'écrit par tradition sous la forme suivante:
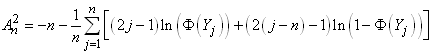 (7.569)
(7.569)
Mais il existe une autre expression simplifiée très
courante. Pour l'établir, nous repartons de l'expression:
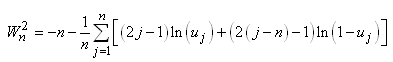 (7.570)
(7.570)
En faisant le changement de variable 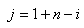 dans
la dernière
somme l'expression: dans
la dernière
somme l'expression:
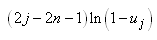 (7.571)
(7.571)
devient:
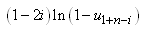 (7.572)
(7.572)
et les bornes de la somme deviennent:
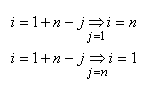 (7.573)
(7.573)
et dès lors:
 (7.574)
(7.574)
Donc:
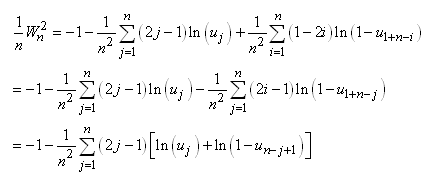 (7.575)
(7.575)
Enfin:
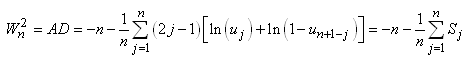 (7.576)
(7.576)
 Exemple: Exemple:
Supposons que nous ayons mesuré les cinq valeurs suivantes:
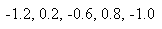 (7.577)
(7.577)
soient ordonnées:
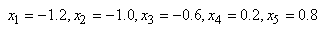 (7.578)
(7.578)
Nous voulons tester l'hypothèse nulle suivante:
où 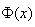 représente
la fonction de répartition
de la loi Normale centrée réduite. Mettre en place le calcul
de l'indice AD dans un logiciel comme la version française
de Microsoft Excel 14.0.6123: représente
la fonction de répartition
de la loi Normale centrée réduite. Mettre en place le calcul
de l'indice AD dans un logiciel comme la version française
de Microsoft Excel 14.0.6123:

Figure: 7.40 - Valeurs à tester avec colonnes habituelles dans le tableur
Soit explicitement:

Figure: 7.41 - Formules Excel explicites du tableau principal de la figure précédente
et:

Figure: 7.42 - Formules Excel explicites des deux dernières cellules
Nous obtenons donc la même valeur de l'indicateur AD que
les logiciels de statistiques qui permettent de choisir la loi à comparer
(et donc les paramètres y relatifs). Cependant pour de très petits échantillons
les logiciels de statistiques utilisent la correction suivante (qui nous été impossible
de réobtenir par simulation...):
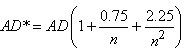 (7.579)
(7.579)
soit dans notre cas AD* vaut environ 0.789.
Ensuite pour calculer la p-value nous devons investiguer
une curiosité... Effectivement si nous la déterminons en faisant
une simulation de Monte-Carlo comme nous l'avons fait lors de notre démonstration
du test de Kolmogorov-Smirnov en changeant d'abord le contenu de la colonne
A en y mettant des valeurs dynamiques triées:

Figure: 7.43 - Formules Excel explicites des deux dernières cellules
Valeurs provenant donc de la colonne O où nous avons mis:

Figure: 7.44 - Formules génératrices d'une loi Normale pour l'application de Monte-Carlo
Le lecteur remarquera donc que cela revient finalement à comparer
l'échantillon avec une distribution uniforme!!!
En ayant ensuite préparé les colonnes suivantes H, I qui contiendront
les valeurs simulées reportées par le code VBA donné un
peu plus loin et les colonnes L, M qui nous permettent d'avoir la répartition
des valeurs de AD et AD* pour en calculer le centile:

Figure: 7.45 - Colonnes pour le reports du VBA et pour les différents centiles
de AD/AD*
avec le petite code VBA ci-dessous vite fait mal fait:

nous avons alors avec 10'000 simulations la répartition
suivante des valeurs de AD et AD*:

Figure: 7.46 - Centiles des 10'000 simulations
Donc que ce soit pour AD ou AD* la p-value se situe dans notre
cas particulier entre 60% et 75% ce qui correspond aux valeurs tabulées
par Peter A. W. Lewis chez IBM (1961).
Ce qui est curieux et qu'il nous faut justement investiguer c'est
que la grande majorité des logiciels utilisent les formules suivantes
(R.B. D'Augostino et M.A. Stephens, Eds., 1986, Goodness-of-Fit Techniques,
Marcel Dekker) permettant d'éviter les simulations de Monte-Carlo:
 (7.580)
(7.580)
et dans notre cas, l'application de ces formules donnent une
p-value d'environ 4%!!! Valeur que donnent effectivement les logiciels
statistiques! Affaire à suivre
pour trouver d'où vient cette énorme différence... Nous
avons demandé au
support technique d'un éditeur de progiciel statistique américain
de nous expliquer la raison de la différence entre les valeurs tabulées
Peter A.W. Lewis et celles R.B. D'Augostino et M.A. Stephens mais ils n'ont
pas été capables de répondre. Nous avons également
contacté M.A. Stephens lui-même pour qu'il nous communique comment
il avait obtenu ces formules mais nous n'avons jamais eu de réponses...
Donc si quelqu'un trouve un jour la méthode et qu'il souhaite
nous le communiquer... Robustesse
Dans le domaine des statistiques inférentielles et
tests d'hypothèses, la robustesse est un concept récurrent
(les banques sont astreintes au stress testing/crash-test de
leurs modèles
de risque). Nous en avons par ailleurs déjà fait
mention plus haut...
Définitions:
D1. Un test est dit "test robuste"
s'il reste valable alors que les hypothèses d'application
ne sont pas toutes réunies.
Ce peut être une taille d'échantillon un peu faible
ou une loi de probabilité (loi normale pour les tests
paramétriques) qui n'est pas très bien vérifiée.
Par exemple, l'ANOVA est robuste par rapport à l'hypothèse
de normalité mais pas par rapport à celle de l'homoscédasticité
D2. Un indicateur est dit "indicateur
robuste" s'il
est peu sensible à la
présence d'outliers (le coefficient de corrélation,
par exemple, n'est pas très robuste).
D3. Plus généralement, un modèle est
dit "modèle robuste" lorsqu'il
permet un prolongement des résultats
(dans le temps ou pour une population). La robustesse s'applique
aussi bien à une régression multiple qu'à une
grille de score.
Par conséquent, à moins d'être uniquement
descriptives, vos études devront respecter quelques
règles pour que leurs conclusions soient généralisables.
Première condition d'une bonne robustesse: les
données. Intuitivement, chacun sait qu'on ne transforme
pas un cas en généralité (ce qui ne relèverait
pas des statistiques mais des discussions de comptoir). Une
quantité suffisante de données permet de bâtir
des modèles fiables et solides. À titre d'exemple,
des prévisions établies à partir d'une
série chronologique montrant une saisonnalité nécessitent
au moins trois ou quatre ans d'historique.
La quantité ne suffit pas, il faut la qualité.
Mieux vaut s'abstenir que réaliser une étude
sur des informations non fiables qui peuvent conduire à des
décisions coûteuses. Par ailleurs, il convient
d'éliminer ou d'imputer certaines observations
(voir outliers). Si ce n'est pas possible, on se tourne
vers des méthodes adaptées, par exemple celles
qui utilisent la médiane plutôt que la moyenne.

|
|
 9 9  0 0 |
Commentaires:
Warning: mysql_connect() [function.mysql-connect]: [2002] Connection refused (trying to connect via tcp://crawl110.us.archive.org:3306) in /home/www/f9f6c3f0bb515fb7fa59d2c99a31acd3/web/htmlfr/php/commentaires/config/fonctions.lib.php on line 46
Warning: mysql_connect() [function.mysql-connect]: Connection refused in /home/www/f9f6c3f0bb515fb7fa59d2c99a31acd3/web/htmlfr/php/commentaires/config/fonctions.lib.php on line 46
Warning: mysql_select_db() expects parameter 2 to be resource, boolean given in /home/www/f9f6c3f0bb515fb7fa59d2c99a31acd3/web/htmlfr/php/commentaires/config/fonctions.lib.php on line 47
Warning: mysql_query() expects parameter 2 to be resource, boolean given in /home/www/f9f6c3f0bb515fb7fa59d2c99a31acd3/web/htmlfr/php/commentaires/config/fonctions.lib.php on line 50
Warning: mysql_fetch_array() expects parameter 1 to be resource, null given in /home/www/f9f6c3f0bb515fb7fa59d2c99a31acd3/web/htmlfr/php/commentaires/config/fonctions.lib.php on line 51
[] 
Warning: mysql_close() expects parameter 1 to be resource, boolean given in /home/www/f9f6c3f0bb515fb7fa59d2c99a31acd3/web/htmlfr/php/commentaires/config/fonctions.lib.php on line 58
|
|